微机电执行器的设计与分析

2016-11-29史春景邓炬锋郝永平刘双杰

制造业自动化 2016年2期

关键词：蛇形离心力保险机构

史春景，邓炬锋，郝永平，刘双杰

（沈阳理工大学 CAD/CAM技术研究与开发中心，沈阳 110159）

数字信号处理

微机电执行器的设计与分析

史春景，邓炬锋，郝永平，刘双杰

（沈阳理工大学 CAD/CAM技术研究与开发中心，沈阳 110159）

基于发射过程引信保险机构的工作原理，设计一种应用双环境力下的MEMS保险机构。在后坐力和离心力作用下，建立相应的动力学模型，研究了影响保险机构工作的因素。应用ADAMS软件，对MEMS保险机构进行动力学仿真分析，得到相应的运动曲线。计算结果表明，后坐滑块能够在后坐环境下可靠执行动作并运动到位，离心滑块能够在在离心环境、延时电路和拔销器的配合下达到设计要求的延时时间并能够可靠运动到位，并且离心滑块的闭锁机构是合理的。同时安全保险机构在勤务处理时是安全可靠的。

引信；MEMS；环境力；动力学模型；动力学分析；可靠；合理性

0　引言

在国防现代化的进程中，武器逐步向微型化、智能化的方向发展，这就促使引信正在向灵巧化、智能化、小型化的方向发展[1]。针对引信MEMS的小型化，需要突破高可靠性的安全保险机构的设计[2]。早期双环境下的MEMS引信安全保险装置是在1998年Charles H Robinson发表的美国专利提出的[3]。在此基础上Charles H Robinson提出了新的改进结构。这也推动者国内安全保险机构的发展，张继桃提出单环境下的安全保险机构[4]。这些机构为进一步的研究尊定了基础。随着钟表延时机构的加工成本和工艺难度，本文提出一种双环境下的镍制MEMS保险机构，用延时电路和拔销器代替钟表延时机构[5]。同时与单环境下的安全保险机构相比，具有更加可靠性和安全性的特点。这不仅为以后MEMS执行器理论的研究和应用提供参考依据，同时也为MEMS执行器在引信方面的应用奠定了一定的基础。

1　机构基本工作原理

保险机构的整体结构，如图1所示。弹丸受发射药燃烧产生火药气体的作用，从而产生极大的加速度，使安保机构受到后坐力的作用。在后坐力的作用下，后坐滑块平行于弹轴向下运动并使锁头锁死在基板底端。在弹丸做直线运动时，使弹丸旋转，从而产生旋转加速度，使安保机构产生离心力，转销在离心力的作用下解除对离心滑块的限制。当弹丸出炮口之后，激活延时电路，延时电路控制拔销器，使拔销器解除对离心滑块的限制。离心滑块在离心力的作用下运动到如图1所示基板右端的锁槽。最后，离心滑块激活传爆序列，实现执行器的功能。这样一系列动作的完成，实现对执行器的设计。

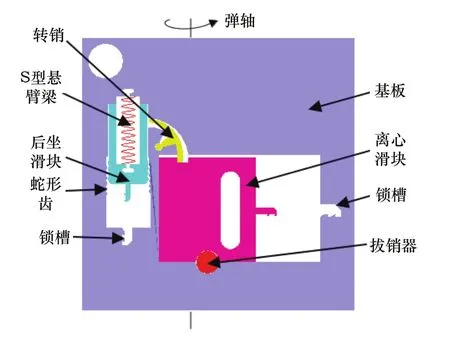
图1　保险机构

2　系统运动学分析

2.1后坐滑块的运动分析

为了找到影响后坐滑块运动的各个相关因素，对后坐机构进行力学分析，如图2所示。

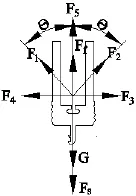
图2　后坐滑块的受力分析

S型悬臂梁竖直方向弹性系数系数计算公式如下[6]：

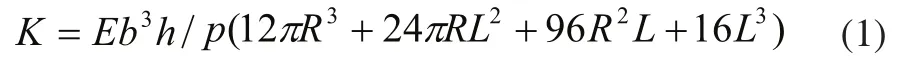
其中E为悬臂梁使用材料的弹性模量，b为悬臂梁线宽，h为悬臂梁厚度，R为悬臂梁弯曲半径，L为悬臂梁线长，p为单元数。

由图2的受力分析和动能定理，可得：

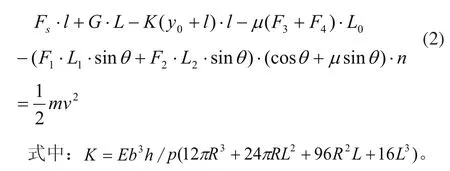
其中m为后坐滑块的质量，FS为后坐力，G后坐滑块的重力，F3为左侧蛇形齿齿顶对后坐滑块侧壁的正压力，F4为右侧蛇形槽齿顶对后坐滑块侧壁的正压力，F1为右侧蛇形齿对右侧后坐滑块齿面的正压力，F2为左侧蛇形齿对左侧后坐滑块齿面的正压力，y0为S型悬臂梁预拉的位移，μ为后坐滑块与基板的摩擦系数，θ为蛇形齿齿顶角的一半，l为锁头没有碰撞锁槽前后坐滑相对基板块移动的竖直位移，L0为蛇形齿齿顶与后坐滑块侧壁相互摩擦时后坐滑块相对基板移动的竖直位移，n为单侧蛇形齿的的个数；L1为左侧蛇形齿中一个齿的齿边与后坐滑块相互作用的长度，L2为右侧蛇形齿中一个齿的齿边与后坐滑块相互作用的长度，v为锁头没有碰撞锁槽前的速度。

后坐滑块能否按预期完成任务主要取决于实际速度的大小。由式(2)知，K、L1、L2、θ和n的大小决定着速度的大小。S型悬臂梁竖直方向弹性系数系数计算公式的分析[7]可知，线宽b主要决定着弹性系数的大小。通过减小线宽b，减小弹性系数，进而可以实现较大的速度，确保后坐滑块能够运动到位，实现解除对隔爆板的限制。同时L1、L2、θ和n的大小也决定着后坐滑块的速度，而L1、L2、θ和n是由蛇形齿决定的。因此，合理的选择蛇形齿参数和线宽b，有利于后坐滑块运动到位。

在ADAMS中，由式(1)调节S型悬臂梁的弹性系数K=1.022×10-3N/mm，预拉力5.13×10-4N，设置设计参数后坐加速度1500g，转速20r/s。进行系统部分中后坐滑块的仿真，仿真时间设置100ms，得到后坐滑块运动的位移—时间曲线如图3所示。

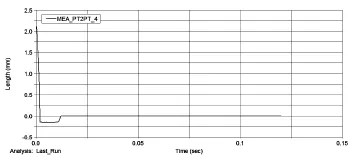
图3　后坐滑块的位移-时间曲线

由图3可知，随着时间的增大，后坐滑块的位移先减小后增大，增大到一定值后成为一恒定常数。同时后坐滑块运动到底部时，所需时间为2.8ms。说明后坐滑块能够运动到位。由图3和式(2)可知，后坐力较大时，后坐滑块向下运动，一直运动到锁槽底部，一定时间以后，随着后坐力的减小，S型悬臂梁的拉力大于后坐力，S型悬臂梁回拉，后坐滑块位移增大，实现闭锁机构闭合。图3验证了式(2)的合理性，也验证了后坐滑块和闭锁机构设计的合理性。

2.2离心滑块的运动分析

转销和离心滑块开始工作时，转销和离心滑块的受力情况如图4和图5所示。

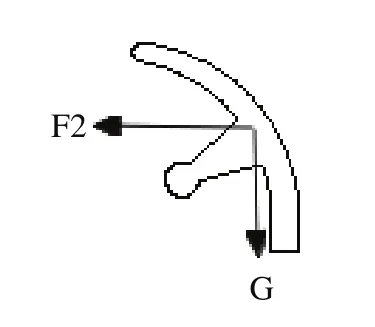
图4　转销的受力分析

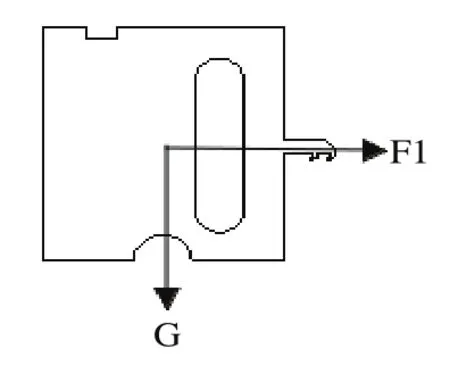
图5　离心滑块的受力分析

由离心滑块受到的离心力F1，转销受到的离心力F2，可得到式(5)和式(6)。

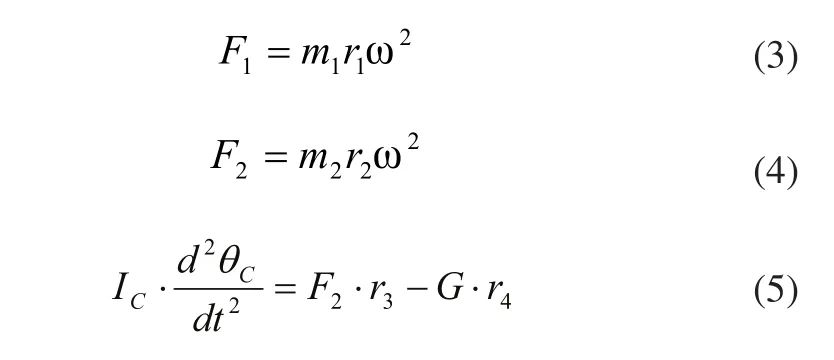
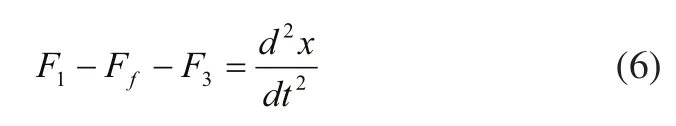
其中m1为离心滑块的质量，m2为转销的质量，r1为离心滑块的质心与弹轴水平方向的距离，r2为转销的质心与弹轴水平方向的距离，IC为转销的转动惯量，r3为转销质心到转销转轴的竖直距离，r4为转销质心到转销转轴的水平距离，Ff为离心滑块受到基板的摩擦力，F3为离心滑块受到转销的阻力。

当弹轴在转销质心左侧时，转销受到的离心力方向与图4相反，故转销在重力和离心力的作用下会发生回复。当弹轴在离心滑块质心右侧时，离心滑块受到的离心力方向与图5相反，故离心滑块不会运动到位。由图5和图6的受力分析可知，当弹轴在转销质心和离心滑块质心之间时，可能会满足转销不回复和离心滑块运动到位。转销运动到位并不发生回复，离心滑块运动到位是机构可靠工作的前提，而转销和离心滑块能否按预期完成任务主要取决于其转销的角加速度和离心滑块运动的加速度。根据式(3)～式(6)可知，r1和r2越大，转销的角加速度越大，离心滑块的加速度越大，转销越不容易回复，转销和离心滑块越容易运动到位。综上可得，弹轴位置在转销质心和离心滑块质心之间，同时合理的弹轴位置有利于转销不发生回复，有利于转销和离心滑块能够运动到位。

为了实现离心滑块的运动，还必须解除拔销器对离心滑块的限制。拔销器的控制是需要电流的激活才能使拔销器拔出，这就需要电路来激活拔销器。但是激活拔销器的具体时间是至关重要的。这就通过加速度计来识别后坐加速度，在达到预定的加速度值后激活后续电路。如图6所示为加速计的工作原理图。调节电源电压，使可移动框架移动，同时在加速度方向受到后坐力的作用下，使加速度计输出信号，并配合延时电路，进而激活拔销器。根据不同的后坐加速度调节相应的电压，使之一一对应，进而实现对后坐加速度的感知，激活拔销器。

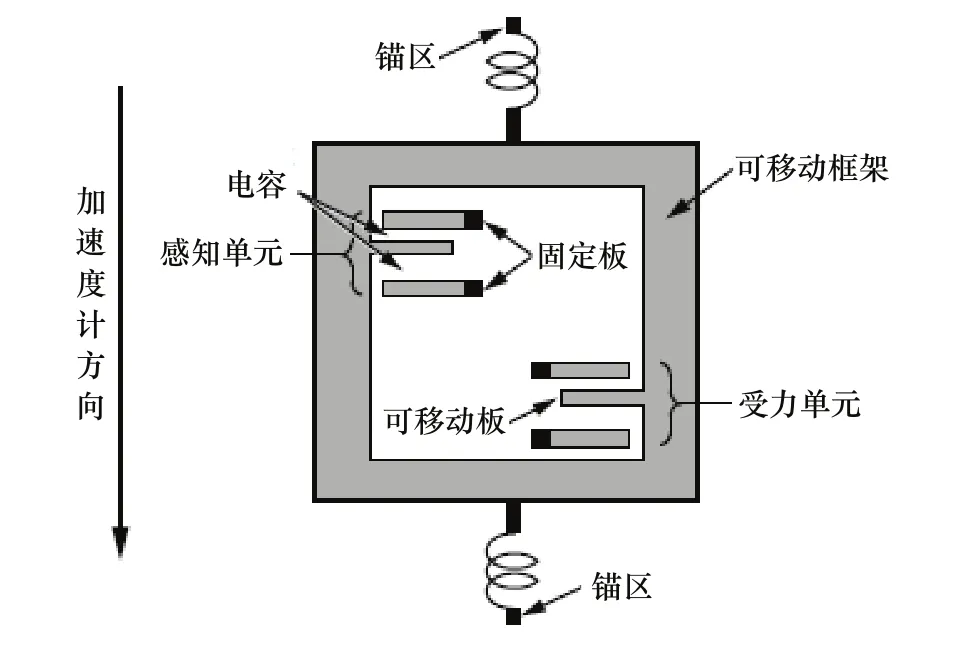
图6　加速度计原理图

9ms之后弹丸出炮口，在ADAMS软件中仿真，选取r1=1.58mm，r2=0.22mm，在加速度计的作用下拔销器在62.5ms时工作，转速20r/s持续工作。得到转销的转角-时间的曲线图和离心滑块的位移—时间曲线，如图7和图8所示。

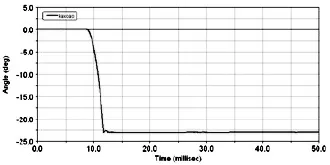
图7　转销的转角—时间曲线图

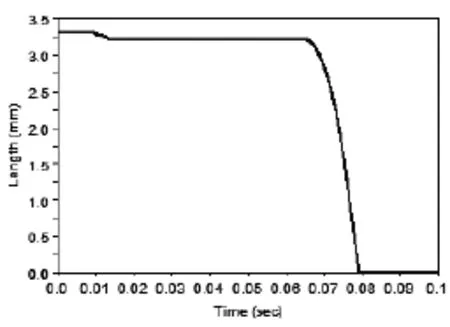
图8　离心滑块的位移—时间曲线

由图7可知，在0～9ms时，转销的转销为0°；在9ms～11.76ms时，转销的转角随着时间的增大而逐渐减小；在大于等于11.76ms时，转角减小为一个恒定值23.1°。9ms大于2.8ms，说明在后坐滑块运动到位以后，转销由静止开始运动，当t=11.76时转销在离心力的作用下转动到位。验证了式(4)和式(5)作为设计依据的合理性，同时验证了弹轴位置设计的合理性。

由图8可知，在0～65ms时，离心滑块为一恒定位移值3.2mm；在65ms～79ms时，离心滑块的位移随着时间的增大而逐渐减小；在大于等于79ms时，位移减小为0。65ms大于62.5ms，说明在拔销器拔出以后，离心滑块由静止开始运动，当t=79ms时离心滑块在离心力的作用下运动到位。验证了式(3)和式(6)设计依据的合理性，同时验证了弹轴位置设计的合理性。

2.3闭锁机构的运动分析

为了实现离心滑块的有效闭锁即离心滑块不发生回复。根据弹轴的持续的转速（20r/s）特点，设计出的闭锁机构，如图9所示。离心滑块的锁头与侧壁1摩擦垂直于弹轴向右运动，离心滑块受到持续存在的离心力作用，离心滑块继续运动，锁头与侧壁2摩擦向右运动，实现离心滑块与锁槽错位相对，形成闭锁机构，实现离心滑块可靠锁定，不发生回复。

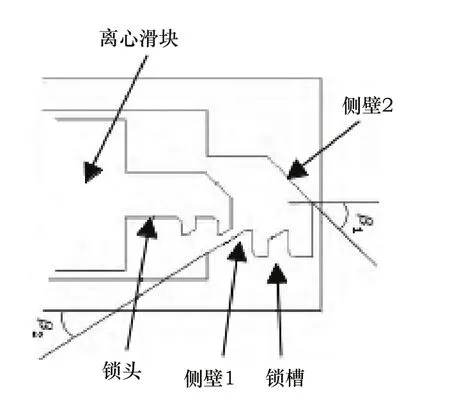
图9　离心滑块的闭锁机构

由图9和工作原理可得闭锁机构的动力学方程：

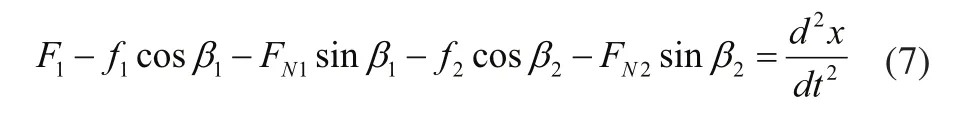
其中f1为离心滑块受到锁槽侧壁1的摩擦力，FN1为锁槽侧壁1对离心滑块的正压力，f2为离心滑块受到锁槽侧壁2的摩擦力，FN2为锁槽侧壁2对离心滑块的正压力。

由式(7)知，离心滑块的质量和离心力一定时，其运动的加速度取决于β1和β2。离心滑块要运动到位，通过调节β1和β2。因此可以通过调节弹轴位置、β1和β2，进而控制离心滑块的运动。正如如图8所示，在65ms～79ms时，离心滑块的位移随着时间的增大而逐渐减小；在大于等于79ms时，位移减小为0。说明离心滑块闭锁机构设计的合理性。

离心滑块加载1500g的转速，锁头受到的应力较大，在ANSYS软件中进行局部应力分析，如图10所示。

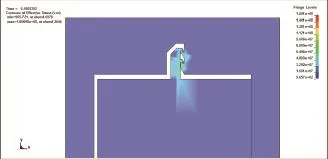
图10　后坐滑块闭锁机构的应力图

镍材料的许用应力为：

式中：n为安全系数，一般取n=4～5。当取σp=E/100，杨氏模量E=210GPa时，由式(8)可计算出[σ]=420MPa～525MPa。由图10可以看出后坐机构的最大应力为160MPa，小于镍材料的许用应力，不会发生失效。离心滑块闭锁机构能够抵抗1500g的转速而不发生变形，说明闭锁机构设计的可靠性。

3　勤务处理安全可靠性分析

当平时勤务处理时，若遇偶然跌落到钢板情况，分析跌落时的冲击载荷对后坐滑块的影响，在ADAMS中对机构加载大小为15000G、持续时间为100µs的冲击载荷，得到后坐滑块距离基板锁槽的位移—时间曲线如图11所示。

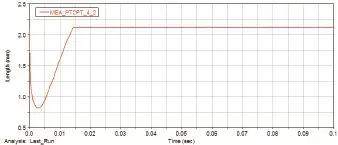
图11　后坐滑块的位移—时间曲线

从图11可以看出：随着时间的增大，后坐滑块的位移值先减小后增大，且增大的最大值为位移的初始值。说明在后坐滑块解除对转销的限制后，后坐滑块在S型悬臂梁拉力的作用下又返回到原初始位置。所以在平时勤务处理时，当后坐滑块偶然运动到位时仍可以恢复到原位。所以硬着路跌落安全。这验证了后坐滑块、蛇形槽和S型悬臂梁设计的合理性和执行器的安全性。

4　结论

通过工作原理的分析，对后坐滑块建立运动方程。通过受力分析和动能定理建立影响后坐力G值的关系式，并得到K、d、a、c和n的大小决定着后坐力G值的大小。通过仿真分析，验证了运动方程和设计的合理性，并得到合理的选择蛇形齿参数和线宽b，有利于后坐滑块运动到位。对隔爆板和后坐滑块建立运动方程，得到弹轴位置在转销质心和离心滑块质心之间。通过仿真分析，验证了运动方程和设计的合理性，并得到合理的弹轴位置有利于转销不发生回复，有利于转销和隔爆板能够运动到位。对离心滑块闭锁机构的分析可得，闭锁机构设计合理且具有高度的可靠性。通过勤务处理的分析可得，该执行器具有可靠性。

[1] 李玲,贾志军.激光引信新技术研究[J].现代电子技术.2010:23-28.

[2] 冯鹏洲,朱继南,吴志亮.美国典型MEMS引信安全保险装置分析[J].探测与控制学报.2007:26-30.

[3] Charles H Robinson, Sliver Spring. Microelectromechanical Systems Safe and Arm Apparatus[P].United States Patent. USP6558329B1.2003:14-25(in chinese).

[4] 张继桃.基于MEMS的安全解除保险机构的设计与试验研究[D].沈阳:沈阳理工大学,2012.

[5] 李占旭,郝永平,纪玉杰,马洪远.MEMS引信钟表机构延时设计的研究[J].机械设计与制造,2011,12:207-208.

[6] 李华,石庚辰,何光.MEMS加工误差对微弹簧力学特性的影响分析[J].压电与声光,2009,10.

[7] 安晓红,张亚,顾强.引信设计与应用[M].北京:国防工业出版社, 2006.

[8] 吴志亮,常娟,冯鹏洲,朱继南.引信用MEMS平面微弹簧弹性系数分析[J].南京理工大学学报,2008,32(2):140-143.

[9] 曹成茂,张河,丁立波.MEMS技术在引信中的应用研究[J].测控技术,2004,23(10):6-7.

[10] 石庚辰,李华.引信MEMS安全系统研究[J].探测与控制学报,2007,29(6):1-5.

[11] 席占稳,聂伟荣.电磁驱动的引信MEMS解除保险机构[J].探测与控制学报,2009,31(5):1-4.

Design and analysis of the micro-electromechanical actuator

SHI Chun-jing, DENG Ju-feng, HAO Yong-ping, LIU Shuang-jie

TH122

1009-0134(2016)02-0005-04