动中通系统中齿轮接触应力分析
2016-11-29王启申袁培江
王启申,郑 罕,袁培江
(1.北京航天控制仪器研究所,北京 100854;2.北京航空航天大学 机械设计及自动化学院,北京 100191)
动中通系统中齿轮接触应力分析
王启申1,郑 罕1,袁培江2
(1.北京航天控制仪器研究所,北京 100854;2.北京航空航天大学 机械设计及自动化学院,北京 100191)
详细阐述了在Pro/E中精确建立齿轮模型的方法及一对啮合直齿轮的装配步骤。将齿轮副导入Workbench中,进行齿轮接触应力分析。仿真结果表明,依据赫兹理论的传统计算结果偏于保守,而利用有限元分析可以得到较为准确的结果。因此,利用有限元分析的方法,可以优化设计动中通结构,实现轻量化。
动中通;齿轮传动;应力分析
0 引言
“动中通”系统是在载体晃动、移动中,仍能通过同步卫星保持正常的通信网络,接收卫星通信信号天线系统,主要应用于车船等移动载体在行进时的实时通信[1,2]。随着动中通系统性能的不断提高,目前已经在直升机、无人机等飞行器中安装使用。齿轮传动因其传动效率高、结构紧凑、工作可靠、传动比稳定等特点[3],本所研制的动中通系统中方位、俯仰、极化均采用齿轮传动。因此,齿轮传动的稳定性直接影响动中通系统的通信性能。
1 齿轮的精确建模
Pro/E是现今主流三维造型软件之一,以参数化著称,是参数化技术的最早应用者。在Pro/E中可以对齿轮啮合进行精确建模。
1.1齿轮参数
渐开线直齿轮基本参数[4]:模数m,齿数z,压力角α,齿顶高系数及顶隙系数c*。则齿轮基本几何尺寸计算公式如表1所示。

表1 齿轮基本几何尺寸
在Pro/E中,根据表1齿轮各参数与基本参数之间的关系,利用参数化建模方法,可以建立精确的齿轮模型。随着Pro/E的应用越来越广泛,一套Pro/E标准零件库也被开发出来。根据现有Pro/E标准零件库,直接调取齿轮模型,再利用Pro/E中零件再生菜单,如图1所示。
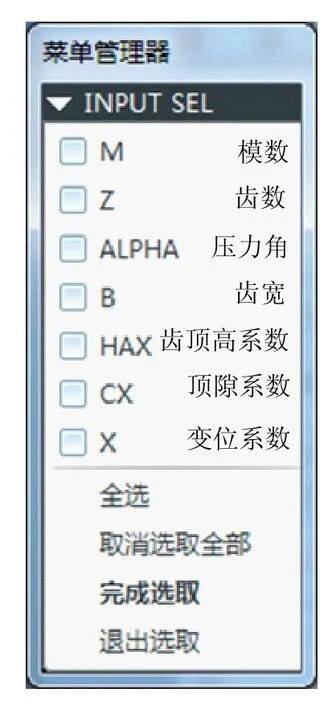
图1 Proe中再生齿轮菜单
重新输入齿轮的基本参数,即可生成齿轮模型。利用上述方法,建立如表2所示参数齿轮。

表2 齿轮基本参数
1.2齿轮啮合装配
1)计算两个啮合齿轮的中心距,建立两个轴A1、A2,使得A1、A2之间的距离为计算所得的中心距。
2)加载小齿轮,利用销钉关系,将小齿轮轴与A1轴轴对齐,小齿轮的一个端面与ASM_FRONT重合,HF_DAM面与ASM_TOP重合。加载大齿轮,同小齿轮装配方式。再将大齿轮的HF_DAM面旋转180/Z2即可。一对处于啮合状态的齿轮如图2所示。

图2 Pro/E中一对啮合的齿轮
2 啮合齿轮的有限元分析
将Pro/E中的齿轮啮合模型转换为stp格式导入Workbench中,分析之前,需完成以下步骤:
2.1赋予材料属性
大小齿轮的材料属性如表3所示。

表3 齿轮材料属性
2.2建立接触对
Workbench中,有三种接触方式:点点接触、点面接触和面面接触。齿轮啮合本是两齿面的相切接触,但在齿轮啮合的过程中,由于齿的变形,使得接触区域为接触线附近的面上,因此本文选择面面接触方式。
设置两个接触对[5],如图2所示,建立小齿轮的齿面1与大齿轮的齿面3之间的接触,接触类型为摩擦接触,摩擦系数设为0.1,将法向刚度因子设置为1。同理设置齿面2与齿面4之间的接触。
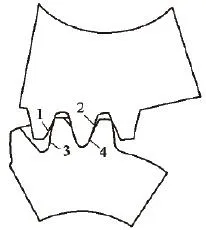
图3 设置齿轮接触对
2.3划分网格
有限元网格划分是有限元分析的重要步骤。网格质量直接影响仿真结果及仿真时间,较高的网格数量可以得到较为精确的仿真结果,但是会增加仿真时间,同时也对计算机资源有较高要求。本文对齿轮划分网格如图3所示,为了提高仿真结果的准确性,对齿轮接触区域进行网格细化。

图4 齿轮网格划分
2.4边界条件及载荷
在小齿轮中心孔表面添加Cylinder Support,并将切向自由度(Tangential)设置为Free。在大齿轮中心孔表面添加Cylinder Support2。根据动中通系统俯仰电机最大扭矩是96Nmm,经减速比是66的减速机后,小齿轮受有力矩96×66=6336Nmm。因此,小齿轮中心孔表面施加扭矩6336Nmm。
【】【】
2.5求解
在完成以上步骤后,即可对齿轮模型进行求解。求解结果如图5所示。由图5可知,接触应力最大为
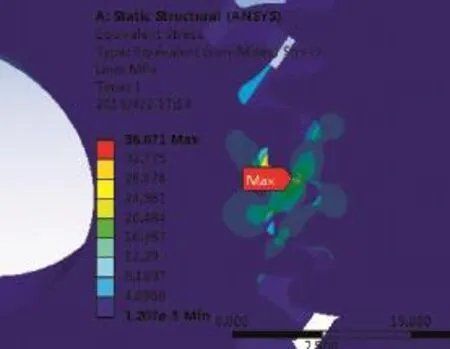
图5 齿轮等效接触应力分布图
3 理论计算与分析
3.1理论计算
根据文献[2],齿轮接触采取两弹性圆柱体接触模型,根据赫兹(Hertz)计算公式,齿轮接触应力σH计算:
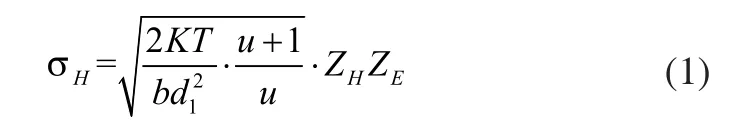
式中:K为载荷系数;
u为传动比;
ZE为弹性影响系数;
ZH为区域系数,对于标准直齿轮α=20°时,ZH=2.5;
在Workbench中由于是静力学分析,为了验证仿真结果与理论计算之间的关系,取载荷系数K为1。
将表2、表3参数分别带入式(1),得出齿轮接触应力的理论计算值:与仿真值相差11.5%。
3.2结果分析
由第2部分得到的仿真值与第3部分计算的理论值可知,齿轮接触应力的仿真值小于理论计算值,这是由于赫兹理论公式做了很多假设与简化,计算偏于保守,给予在实际问题中很大的富余量。
4 结论
本文首先在Pro/E中建立了精确的齿轮模型,经装配后形成齿轮副,导入Workbench中进行有限元分析其接触应力。
1)有限元分析与传统理论公式计算齿轮接触应力基本一致,表明本文所建立的齿轮副三维模型和有限元分析模型是准确可信的。
2)传统赫兹理论计算齿轮接触应力偏于保守,利用Workbench分析,可以得到较为准确的结果,为设计人员提供更为可靠的参考。
3)利用有限元分析软件能有效的对齿轮进行模拟仿真,从而为齿轮的动态设计、优化设计和可靠性设计打下基础。
[1] 邬江,曾宪超,王盛.“动中通”三轴天线跟踪机理研究[J].导航与控制,2013,12(3):52-55.
[2] 张金余,郭刚,韩军海,魏宗康,叶涛.“动中通”系统中极化角的计算[J].导航与控制,2011,10(1):20-23.
[3] 濮良贵,纪名刚.机械设计[M].第七版.北京:高等教育出版社,2001.
[4] 孙桓,陈作模.机械原理[M].第六版.北京:高等教育出版社,2001.
[5] 雷镭,武宝林,谢新兵.基于ANSYS有限元软件的直齿轮接触应力分析[J].机械传动,2006,30(2):50-51,59.
Analysis of contact stress for gear in satcom on the move system
WANG Qi-shen1, ZHENG Han1, YUAN Pei-jiang2
TH132
A
1009-0134(2016)02-0001-03
2015-10-20
国家自然基金资助项目(61375085)
王启申(1988 -),男,安徽太和人,工程师,硕士,主要从事动中通产品的机械系统设计与仿真工作。
