改进的非线性信号小波消噪方法

2016-11-29齐春辉李其建

制造业自动化 2016年2期

关键词：极大值方根小波

齐春辉，李其建

（1.河北工业大学机械工程学院，天津 300130；2.西安交通大学机械工程学院，西安 710049）

加工与制造

改进的非线性信号小波消噪方法

齐春辉1，李其建2

（1.河北工业大学机械工程学院，天津 300130；2.西安交通大学机械工程学院，西安 710049）

选用小波消噪用于生产系统的非线性传感器信号消噪，以便通过判断系统状态来找出系统运行过程中生产出次品和不合格品的因素。简介小波消噪的三种常用方法，并进行比较和分析。以均方误差最小、信噪比最大为原则，筛选出最适合的消噪方法，对其进行融合改进。MATLAB仿真证明改进后消噪效果显著提升。

系统状态；非线性信号；小波消噪；MATLAB

0　引言

为生产装备系统匹配合适的传感器，通过采集到的传感器信号判断出系统的生产状态，以便快速查找有问题的生产环节。由于传感器信号极易受到噪声的干扰，严重影响传感器信号的识别和检测，因此对传感器信号进行消噪迫在眉睫。本文选择小波消噪方法对非线性信号去噪，并对小波消噪加以改进，使非线性信号更容易识别和检测。

1　小波消噪方法

基于小波理论的消噪方法是一种利用小波变换把噪声从信号中分离出来的滤波方法。其原理是把原始信号的有效部分和噪声投影到不同的正交频带上，把有效信号和噪声信号区分开来，实现消噪的目的[1]。

小波分析的方法具有多分辨分析的特点能够对信号的任何细节进行多分辨的时域分析。小波的消噪方法[2,3]有很多，比较常用的方法有分解与重构法、模极大值法和阈值法等。以下将对这几种方法进行分析比较研究。

1.1分解与重构法

分解与重构法实际上是利用了小波变换多分辨分析的特性，把原始信号的有效部分和噪声部分分解到不同的正交频带上，然后把噪声所在的频带去除，保留有用信号的频带，然后对信号进行小波重构，使信号恢复，得到消噪后的信号。

对信号f(t)进行离散采样，得到一组数据fk（k=1，2，…，N），fk=c1,k，将信号f(t)进行小波变换分解，计算公式为：

式中：cj,k为尺度系数，h、g为正交的镜像滤波器组，dj,k为小波系数，j为小波分解的层数，N为离散采样点1的数量。

小波重构是小波分解的逆过程，计算公式为：

利用分解与重构法消噪后的信号可能还会存在一些噪声，为提高消噪的效果可以将消噪后的信号再次进行消噪处理，通过多次处理让信号的噪声逐步减小。

1.2模极大值法

函数f(x)在某一点的Lip指数的大小表示了该点奇异性的大小。a越小，表示该点存在突变越明显，奇异性也就越大；a越大，表示该点越光滑。对于不同的信号，得到的a的值也各不相同，对于一般的信号a≥0，脉冲信号a=-1，信号中存在白噪声时。

从上式可以看出，对于一般信号来说，由于其a≥0，可以看出经过小波变换得到的模极大值将会随着j的增大而逐渐增大；对于白噪声来说，由于其a＜0，可以看出经过小波变换得到的模极大值将会随着j的增大而逐渐减小，因此可以通过观察模极大值在不同尺度间的变化规律来实现消噪的目的。若点的值随着尺度的增加而减小，则此点对应于噪声的极值点，可以去除；若点的值随着尺度的增加而增大，则此点对应于有用信号的极值点，保留此点。然后再用交替投影法对保留的模极大值点进行重建，便可以得到消噪之后的信号。

1.3阈值消噪法

阈值法是基于阈值处理的小波变换方法。为了便于处理，对一个原始信号进行叠加高斯白噪声，即（zi为叠加的高斯白噪声；为噪声级）。

若想从以上叠加了噪声的信号yi中恢复出原始的信号xi，可以采用Donoho的消噪方法[9]，步骤如下：

1）对含有高斯白噪声的信号进行小波变换。首先选取合适的小波分解层数j和合适的小波基，利用分解与重构法将信号分解至j层，得到分解系数。

2）对得到的分解系数进行阈值处理，常用的阈值处理方法有两种：

硬阈值：

软阈值：

3）将阈值处理后的分解系数进行小波逆变换，即采用分解与重构的方法进行信号重构，则可以得到恢复的原始信号估计值达到了去除噪声的目的。

阈值消噪法是把含有高斯白噪声的信号进行能量集中，反应在少量的小波系数上，由于白噪声经过小波变换投影之后得到的还是白噪声，且幅度不变，因而只要比较小波分解后的小波系数，幅值比较大的是有效信号，幅值比较小且能量比较分散的是白噪声。所以只要选择一个合适的阈值，能够将小波系数幅值的大小区分开来，便能够实现去除白噪声的目的。

2　消噪效果衡量方法

信号消噪的效果可以用信噪比（SNR）和均方根误差（RMSE）进行衡量[4]。

均方根误差是指小波消噪后信号与原始信号的均方根误差。计算公式为：

信噪比是指原始信号能量与噪声能量的比值，计算公式为：

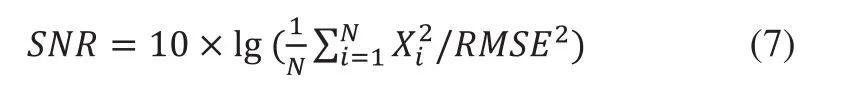
式中：Xi为原始时间序列，为小波消噪后的时间序列，N为时间序列的长度。

一般地，均方根误差越小、信噪比越大的情况下信号消噪的效果越好。针对要处理的信号分别利用分解与重构法、模极大值法和阈值法这三种方法进行前六层消噪，求解均方根误差和信噪比。若对应的均方差误差最小，信噪比最大的为一种方法，则选用这种方法为该信号的消噪方法。若不是同一种方法，则分别选择出对应的均方差误差最小，信噪比最大的方法，将两种方法融合，作为该信号的消噪方法。

3　仿真实验

利用MATLAB自带的一个噪声污染的多普勒效应信号作为原始信号，如图1所示。利用小波消噪的三种方法分别对其消噪，并进行分析，选择适合该信号的最合适的消噪方法。

图1　原始噪声信号

3.1分解与重构消噪法

小波的分析结果和小波基有很大的关系，不同的小波基消噪的效果也各不相同，常用的小波基有sym3、sym5、coif2、coif5、db2和db6等。

经查阅文献，可知用coif2小波基进行去噪处理可以得到较好的效果，用coif2小波基对上述的原始信号进行消噪处理，可以得到前六层去噪后的信号如图2所示。

由图可以看出，随着去噪层数的增加，去噪效果也随着增加，但是层数过大的时候，信号便会出现失真。因而需要选取合适的分解与重构数。

图2　分解与重构消噪法前六层消噪结果图

3.2模极大值消噪法

由原始信号进行前六层模极大值法去噪，结果如图3所示。由图可知模极大值消噪法，随着层数的增加，消噪效果也越来越好，然而层数较多时，信号也会产生失真。

图3　模极大值消噪法前六层消噪结果图

3.3阈值消噪法

利用阈值消噪法进行前六层小波变换，结果如图4所示。由图可知随着层数的增加，阈值消噪法的效果有所增强，然而效果没有前两种方法好。

图4　阈值消噪法前六层消噪结果图

3.4改进后消噪

求解分解与重构法、模极大值法和阈值法的前六层均方根误差和信噪比，结果如表1所示。

由表1可以看出，采用分解与重构方法进行二层消噪时，均方根误差最小；采用模极大值法进行二层消噪时，信噪比最大。

表1　三种方法的前六层均方根误差和信噪比

为尽可能地提高消噪效果[5]，考虑先将分解与重构法和模极大值法这两种方法结合起来，消噪步骤为：

1）对原始信号y0进行模极大值二次消噪，得到消噪后信号为y1，噪声信号r1，r2=y0-y1。

2）对r1进行二次分解与重构，得到除噪后的信号y2，y2与r1的差记为r2。y2认为是有用的信号，噪声保存在r2中。

3）将y1和y2叠加，则得到消噪后的信号。

消噪结果如图5所示。

图5　改进方法消噪结果图

通过计算可以得到二次消噪后信号的均方根误差为0.8632和信噪比为19.5402，而单独利用模极大值法进行二层消噪得到信号的均方根误差为1.0973，信噪比为17.4102，即二次消噪后信号的均方根误差减小了21.33%，信噪比提高了12.23%，说明利用二次消噪的方法比单独利用模极大值法的消噪效果得到了提升。