研究固体火箭发动机封头的卡爪的疲劳寿命

2016-11-29王州博马小康戴源成孟瑞锋

制造业自动化 2016年2期

关键词：弧面封头修正

王州博，马小康，戴源成，杨涛，孟瑞锋

（1.内蒙古工业大学机械学院，呼和浩特 010051；2.深圳市元创兴科技有限公司，深圳 518000）

研究固体火箭发动机封头的卡爪的疲劳寿命

王州博1，马小康1，戴源成2，杨涛1，孟瑞锋1

（1.内蒙古工业大学机械学院，呼和浩特 010051；2.深圳市元创兴科技有限公司，深圳 518000）

固体火箭发动机封头的卡爪是组装固体火箭发动机中极其重要的零件，研究该卡爪的疲劳寿命，确定影响卡爪的重要设计参数，可以对优化其结构设计提供重要理论依据；协同仿真平台ANSYS Workbench，在对其进行疲劳寿命分析时，通过实验数据，采用最小二乘法拟合45号钢材料的S-N曲线，再采用经验公式和平均应力修正理论对S-N曲线进行精确修正，以便求解出更为符合实际的疲劳寿命；通过对火箭封头卡爪的疲劳寿命研究，得出该产品的实际工作的四个微小弧面对其疲劳寿命有很大影响，在疲劳寿命的要求范围内，确定了实际工作的四个微小弧面的面积范围，这对优化设计提供很大帮助。

卡爪；疲劳寿命；ANSYS Workbench；S-N曲线；微小弧面

0　引言

固体火箭发动机由于其结构简单、易于维护、可靠性高等优点，在航空、导弹等领域中已得到广泛应用。目前，由于安全性问题，很多固体火箭发动机的组装还是人工操作，但是，人工组装不仅效率低、成本高，而且安装精度不一致，采用工业自动化装配可保证固体火箭发动机组装具有更高的效率和精度。在做“小型固体火箭发动机封头与燃烧室自动装配工艺研究”的项目研究时，设计了一种自动装配设备，其中，固体火箭发动机封头的卡爪（以下简称卡爪）是与固体火箭发动机封头相啮合，带动其旋转，使其旋入燃烧室，起到密封作用，其实物图如图1所示。自动装配时，固体火箭发动机的燃烧室是装有燃料的，因此，卡爪在整个装配机械结构中是非常重要的零件，在工作过程中，如果卡爪发生破坏，将不能保证火箭封头对火箭壳体燃烧室的密封性，密封性不足时，会造成燃料泄露，使火箭在发射时缺少精确性；更为严重的情况是，破坏可能产生的火花，将直接与固体火箭燃烧室的燃料接触，产生爆炸，这将导致严重的损失和伤亡，从而不仅要对卡爪要求有足够的强度、刚度，同时还需要具有较高的可靠性，所以研究卡爪的疲劳寿命对组装固体火箭发动机具有重要意义。

对产品进行虚拟疲劳分析国内外已经有过很多研究，在国内、王彦伟、罗继伟[1]等人对有限元的疲劳分析方法进行过深入研究，使用这些虚拟疲劳分析方法，高东明、王德成[2]等人对草地切根机切刀进行过疲劳寿命分析，苏高峰、薄玉成[3]等人对杆端向心关节轴承进行过疲劳寿命分析研究，但是这些疲劳寿命分析中，对材料的应力-寿命（S-N）曲线都没有经过很好的修正，使得最后的仿真结果与实际有一定的偏差，此篇文章通过王彦伟，罗继伟等人所介绍的有限元的疲劳分析方法，经过实际试验得到的材料S-N曲线，根据谢金标、姚卫星、吉凤贤[4,5]，还有傅惠民，高镇同，梁美训[6]等人关于疲劳S-N曲线拟合方法的研究结果，对实验得到的S-N数据进行拟合，然后采用相应的经验公式[7]和Gerber平均应力修正理论[8]对其进行精确修正，使得仿真结果与实际基本相符，对设计卡爪具有一定的指导意义。

图1　卡爪

1　卡爪模型的静力结构分析

利用Pro/E建立卡爪有限元模型，导入Workbench中，并设置材料参数，卡爪的材料为45号钢，杨氏模量E=2×1011Pa,泊松比µ=0.3，质量密度ρ=7850kg/m3。

1.1卡爪受力载荷的计算和边界条件的确定

载荷：工作中，卡爪采用普通A型平键传动，端面四爪之间的间隙与固体火箭封头啮合，带动其旋转，因此，端面四爪微小弧面S1为实际工作面，因此在Workbench中需要分别对S1和键槽工作面S2施加工作载荷σ1、σ2。通过扭矩传感器测得卡爪在工作中最大扭矩T=150N·m，本文采用力矩平衡法计算，由理论公式：

式中l为力矩；计算得：σ2=94.78MPa，而σ1的大小由四个微小弧面在实际中工作的接触面S1的大小来决定，因此S1的取值对实际的工作载荷有很大的影响，暂时设计S1=27mm2，计算得：σ1=81.7MPa。

约束：工作中，卡爪只可以绕X轴可以转动。因此，需要在内圆柱面施加径向和轴向圆柱面约束，并且在底面施加X、Y、Z方向位移为0mm的约束。

1.2模型网格划分和求解

为了使简化软件计算，因此划分网格时，只在重要部位将网格元素大小（Element Size）设为1mm，而其余部分设为6mm。得到60319个节点，35916个单元元素，网格划分结果如图2所示。

图2　网格划分结果

插入等效应力（Equivalent Stress）进行求解，得到应力云图，最大应力: σmax=204.43MPa。如图3所示。

图3　静力分析云图

2　卡爪的疲劳寿命分析

2.1疲劳分析的流程

在ANSYS Workbench中，疲劳模块拓展程序（Fatigue Module add-on）采用的是基于应力疲劳（stressbased）理论，它适用于高周疲劳，使用Workbench软件进行虚拟疲劳分析时，首先需要对有限元模型进行静力分析，然后使用ANSYS Workbench中疲劳分析模块（Fatigue Tool），插入疲劳分析模块（Fatigue Tool）后，在选择合适的疲劳损伤累积规则后，疲劳分析系统自动进行疲劳分析，计算出零件的疲劳寿命分布，以帮助设计人员判断设计寿命是否达到，或进行寿命优化设计。图4为虚拟疲劳分析流程图[9]。

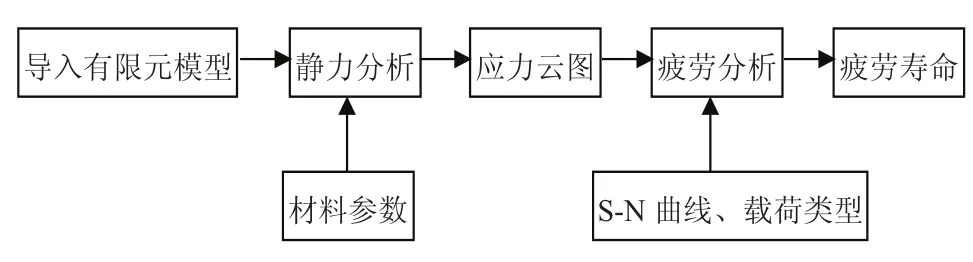
图4　虚拟疲劳分析流程图

2.2确定疲劳分析方法

疲劳通常分为两类，高周疲劳和低周疲劳。高周疲劳受应力幅控制，一般循环应力的最大应力低于材料屈服极限，弹性变形居主导地位；而低周疲劳主要受应变幅控制，一般循环应力高于材料屈服极限，塑性变形居主导地位[7]。根据疲劳破坏的形式不同，工程中常用有三种疲劳分析方法：名义应力法（也叫应力-寿命设计法）、局部应力应变法和损伤容限法，局部应力应变法只适用于零部件的应力集中处发生了塑性变形的低周疲劳，损伤容限法则是随着断裂力学的应用和发展, 将断裂力学中临界裂纹长度和裂纹扩展速度综合考虑而形成的一种疲劳分析方法，而名义应力法主要用于对弹性变形居主导地位的高周疲劳寿命进行计算[1]。

从上述分析的应力云图可知，卡爪在最薄弱部分的最大von-Mises应力为204.43MPa，低于材料的屈服极限345MPa[10]，因此，在疲劳分析中，弹性变形居主导地位，这样便可采用名义应力法对卡爪进行疲劳分析。名义应力法的关键在于确定卡爪的S-N曲线，精确的S-N曲线将确保疲劳分析结果更加准确和更具参考价值。

2.3估算材料的S-N曲线

材料的疲劳极限和S-N曲线，只能够代表标准光滑试样的疲劳性能，一般根据实验数据，采用最小二乘法来确定最佳拟合直线[4,6]，其拟合方程为：

式中σ-1为对称循环持久极限；X，Y为待定常数；Np为疲劳寿命。

X，Y由以下公式确定：

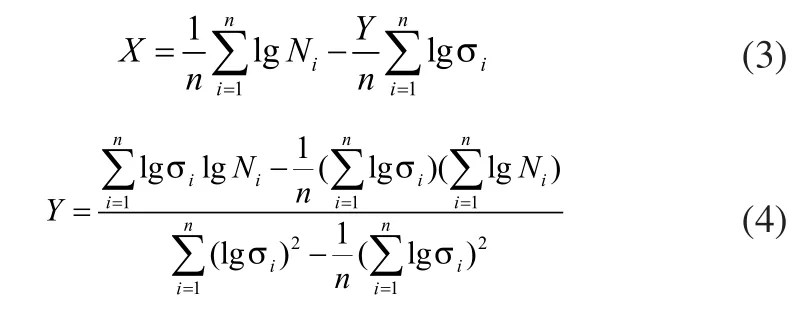
根据作者苏彬在论文《45号钢在不同应力比循环载荷下的微动疲劳特性》[11]中，可获得在轴向循环载荷应力比为0下，对45号钢做的疲劳寿命曲线实验数据，如表1所示，其中，R为轴向循环载荷应力比，R=σmin/σmax；σmax为轴向循环载荷的最大应力；σmin为轴向循环载荷的最小应力；N为45号钢微动疲劳寿命；S为轴向循环载荷应力幅S=(σmax-σmin)/2。

表1　45号钢微动疲劳寿命实验数据

根据式(3)、式(4)可计算得X=28.5342、Y=-10.3681所以拟合曲线表达式为：

2.4修正构件外形、尺寸、表面质量等因素对S-N曲线的影响

上述所拟合曲线方程是常温下用光滑小试样测定的。但实际构件外形、尺寸、表面质量等都将影响疲劳极限的数值，因此需要对S-N曲线进行修正。疲劳强度降低系数KσD是包含了影响疲劳极限诸多因素的一个综合因子，该系数的选择将对S-N曲线的修正产生很大影响，有多种经验表达公式[7]，常用的有：

式中，Kσ为有效应力集中因数，εσ为尺寸因数，β为表面质量因数；这三种表达式主要的不同是对表面加工系数β的处理不同，公式(6)认为Kσ、εσ、β三者互不影响，式(8)认为β随着Kσ/εσ值增加而减小，式(8)认为β随着Kσ的增加而减弱。从试用的情况来看，在Kσ较低的范围内三者的差别不大。在Kσ较大的情况下，式(6)的结果偏大，而式(7)的结果比式(8)的结果略大。虽然关于表面粗糙度等表面加工情况对有效应力集中因数的影响，并没有太多的研究，但根据相关研究结果可以推断，随着疲劳缺口变尖锐，表面粗糙度的影响不应增大，考虑材料强度对表面加工系数的影响，而对于塑性比较好的低中强度钢适合采用式(7)，高强度钢适合采用式(8)[8]。

该系数对疲劳极限的修正公式为：

所以数据计算采用式(7)，查询相关书籍[1]得：Kσ=1.3，εσ=0.84，β=0.95；得KσD=1.60。根据式(5)、式(9)计算出数据，如表2所示。

表2　疲劳寿命与疲劳极限数据

将该数据输入到Workbench中，绘制出S-N曲线如图5所示。

图5　S-N曲线

2.5平均应力对疲劳极限的影响

影响疲劳极限的因素除了上述构件的外形、尺寸和表面质量以外，平均应力也是一个重要因素[12]。在一定的平均应力范围内，压缩的平均应力可以提高疲劳极限，拉伸的平均应力降低疲劳极限，修正平均应力的影响可以采用平均应力修正理论，ANSYS Workbench提供Goodman理论、Soderberg理论和Gerber理论三种修正理论，Goodman理论适用于低韧性材料，对压缩平均应力没能做修正，Soderberg理论比Goodman理论更保守，并且在有些情况下可用于脆性材料，Gerber理论能够对韧性材料的拉伸平均应力提供很好的拟合，但它不能正确预测出压缩平均应力的有害影响[8]。以下求解中采用的是Gerber平均应力修正理论。

图6　寿命云图

2.6载荷类型设置和求解卡爪的疲劳寿命

在工作过程中，卡爪一直在做速度恒定定的旋转动作，四个微小弧面所承受的载荷是随时间按正弦曲线作周期性变化的应力，并且是应力比r=0的脉动循环，由于键槽工作面上的载荷与四个微小弧面上的载荷相互平衡，因此键槽工作面上的载荷也是应力比r=0的脉动循环，从而载荷类型设置在Workbench中为脉动循环（Zero-Based）。

另外，虽然S-N曲线上述已经经过修正，但Workbench还提供了疲劳强度因子的修正方法，为了获得比较高的安全系数，保守地取疲劳强度因子Kf=0.8，并且平均应力修正理论设置为Gerber方法。

疲劳结果求解：在Fatigue Tool中插入“life”，求解之后，得到life云图，life云图显示由于疲劳作用直到失效的循环次数，如图8所示。

3　结论

上述分析对45号钢材料的疲劳试验数据是采用最小二乘法进行了拟合，得到了拟合曲线，但影响该曲线的因素有很多，主要因素是火箭封头卡爪的外形、尺寸和表面质量，以及平均应力的影响，通过经验公式和Gerber平均应力修正理论对该拟合S-N曲线进行修正，得到最终的S-N曲线。基于该S-N曲线，通过Workbench对火箭封头卡爪进行疲劳寿命分析，获得的卡爪寿命云图是符合卡爪实际结构的；从卡爪的寿命云图中可以看出，设计参数微小弧面的实际接触面积S1为27mm2时，在最危险区域，卡爪的疲劳寿命只达到了2.3万次以上循环。因此，要改善卡爪的疲劳寿命，微小弧面的实际接触面积S1必须大于27mm2，而在实际加工过程中，实际接触面积S1越大，意味着加工卡爪的难度和成本增大，所以在要保证一定的疲劳寿命的情况下，并且需要考虑难度与成本时，通过Workbench对火箭封头卡爪进行疲劳寿命分析，将为重要的设计参数实际接触面积S1提供一个合理数值，这在设计过程中省去了大量繁琐的计算，很有效的提高了工作效率。

[1] 王彦伟,罗继伟,叶军,陈立平.基于有限元的疲劳分析方法及实践[J].机械设计与制造,2008,1(1):22-24.

[2] 高东明,王德成,王光辉,马晓刚,袁洪方.草地切根机切刀的疲劳寿命分析[J].江苏大学学报（自然科学版）2012,33(3):283-287.

[3] 苏高峰,薄玉成,孔静静,曲振森,徐煜星.杆端向心关节轴承动应力下疲劳寿命分析研究[J].机械设计,2013.33(3):89-92.

[4] 谢金标,姚卫星.疲劳S-N曲线拟合的双加权最小二乘法[J].宇航学报,2010,31(6):1661-1665.

[5] 吉凤贤,姚卫星.疲劳S-N曲线的加权最小二乘法拟合[J].南京航空航天大学学报,2004,21(1):53-57.

[6] 傅惠民,高镇同,梁美训.S-N曲线拟合法[J].北京航空学院学报,1987,11(1):115-119.

[7] 赵少汴,抗疲劳设计[M].北京:机械工业出版社,1994.

[8] 徐灏.疲劳强度[M].北京:高等教育出版社,1988.

[9] 潘金坤.大客车横向稳定杆的虚拟疲劳分析[J].制造业自动化,2011.33(1):145-147.

[10] 成大先.机械设计手册[M].北京:化学工业出版社,2010.

[11] 苏彬.45号钢在不同应力比循环载荷下的微动疲劳特性[D].浙江工业大学:化工过程机械.2010:30-42.

[12] 李淑兰,杨玉芬,徐人平.平均应力对45钢P-S-N曲线的影响[J].理化检验·物理分册,2007,43(12):611-613.