基于支持向量回归的整体翼梁结构应力强度因子预测技术

翟新康，王斌团，李小鹏，张彦军

（中航工业一飞院，西安 710089）

基于支持向量回归的整体翼梁结构应力强度因子预测技术

翟新康，王斌团，李小鹏，张彦军

（中航工业一飞院，西安 710089）

利用支持向量回归机理论，通过对样本空间的回归分析，构建了以整体翼梁结构截面参数尺寸为输入、应力强度因子为输出的回归模型。通过该模型，可以对任意一组参数下含裂纹整体翼梁结构裂纹尖端应力强度因子进行预测。经计算，整体翼梁裂纹尖端应力强度因子的预测值与有限元分析计算值的绝对误差平均值分别为1.2%，满足工程要求。采用该方法进行结构参数灵敏度分析和优化设计，可以大大减少计算量，提出的分析技术可供飞机结构设计参考。

支持向量回归；整体翼梁；含裂纹结构；应力强度因子

0　引言

对于含裂纹的整体翼梁结构，其裂纹尖端应力强度因子不能直接通过《应力强度因子手册》或相应的计算公式得到，虽然通过有限元的方法可以计算，但是却非常耗时。在对整体翼梁结构进行参数灵敏度分析和优化设计时，需要计算成千上万组参数下的应力强度因子，若每一步都调用有限元程序，则效率会十分低下。为了解决这个问题，提出了建立基于支持向量机的应力强度因子代理模型，该模型反映了整体翼梁结构截面参数与应力强度因子的关系，基于该模型，可以通过预测，得到任一组结构参数下的应力强度因子。

1　支持向量回归机介绍

支持向量机（Support Vector Machine，简称SVM），是20世纪90年代Vapnik等人提出的将统计理论、机器学习、优化理论等有机结合，根据结构风险最小化原则来自动学习模型的结构，通过调节控制参数来改变模型结构，成为继神经网络、模糊辨识等方法之后用于黑箱辨识的热点方法。支持向量机能较好地解决小样本、非线性、高维数识别和局部极小点等实际问题。

1.1支持向量回归机算法

支持向量回归的基本思想是，针对不满足线性关系的样本集(x1,y1),(x2,y2),…,(xm,ym)，通过输入空间到输出空间的非线性映射φ，将样本集中的数据x映射到高维空间F，并在特征空间F中用下述函数进行线性回归，即：

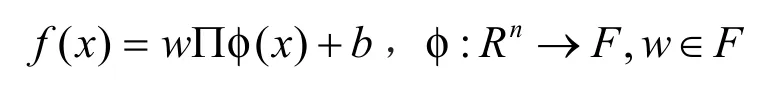
上式中，b为阈值，w为回归系数向量。影响w的因素有：经验风险的总和以及使其在高维空间平坦的。

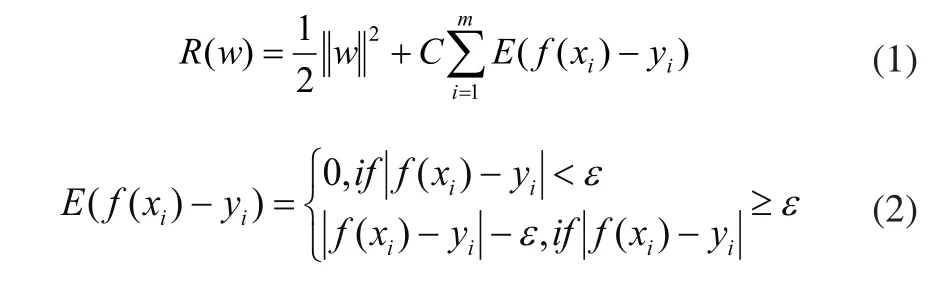
式中，m为训练样本个数，E(f(xi)-yi)是损失函数，C为惩罚因子。

为控制函数的复杂性，应使线性回归函数尽量平坦，并考虑可能超出精度的回归误差，引入松弛因子ξ和ξ*，以处理不满足上式的数据点。根据统计学习理论的结构风险最小化准则，SVR方法通过最小化目标函数来确定w和b：

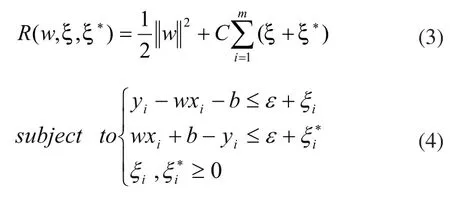
上式中，第一项是使回归函数更为平坦，泛化能力更好；第二项则为减少误差，惩罚因子C是一个常数，且C＞0，用来控制对超出误差ε的样本的惩罚程度。建立拉格朗日方程：

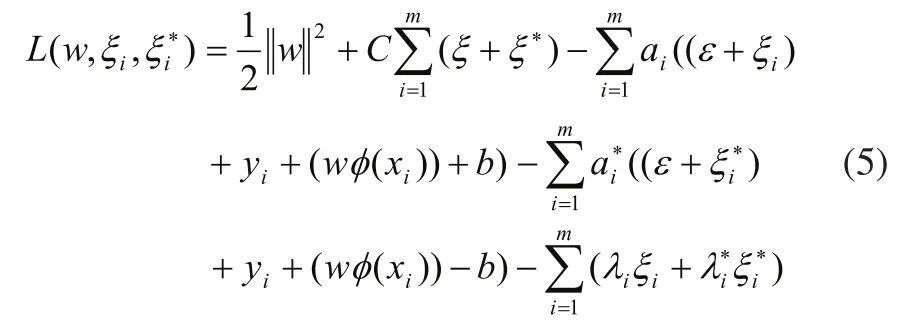
代入式(5)，可以得到对偶优化问题：

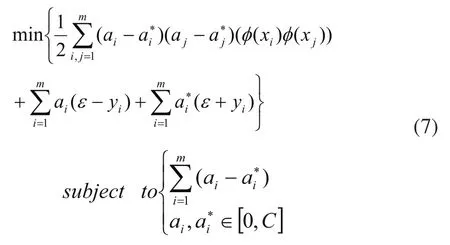
由此，SVM的函数回归问题就可以归结为二次规划问题(7)。求解该二次规划问题，可以得到用训练样本点表示的w：

式中，ai和是最小化的解。由此可求得线性回归函数：

1.2支持向量机建立回归模型的流程

采用MATLAB上的LIBSVM工具箱进行回归模型建立。采用高斯径向基核函数建立模型。影响支持向量机回归模型预测精度和泛化能力的参数包括惩罚函数C、不敏感参数ε以及核参数σ等。

高斯径向基核函数确定后，其参数σ、C和ε可以认为调节。这里采用数学规划法的方式来寻求最优参数C、ε和σ，然后用参数C、ε和σ来训练整个训练集。

对模型的检验有两个评价指标：

均方误差：

相关系数：

其中，n代表样本点个数；yi代表响应的真实值代表预测值；代表响应的平均值。MSE越趋近于0，说明模型的精度越高；R2在[0,1]之间变化，其值越接近1说明误差越小，拟合精度越高。其流程图如图1所示。

图1　建立代理模型流程图

2　整体翼梁结构参数及应力强度因子计算

翼梁结构参数如图2所示。梁的材料为7050-T7451，弹性模量E=70Gpa，泊松比μ=0.33，强度极限断裂韧性

为了分析止裂筋条对结构应力强度因子的影响，这里只分析腹板到止裂筋条这一段路径的裂纹扩展。假设初始裂纹存在于翼梁中间，下缘条完全断裂，并扩展至腹板上25mm处；临界裂纹位置为止裂筋条。假设整体翼梁结构上的裂纹按直线扩展。按照常规的有限元理论建模并进行裂尖有限元应力强度因子计算[1]。

3　基于支持向量回归机应力强度因子代理模型的建立

3.1样本空间设计

选择拉丁超立方的取样方式，使样本均匀地分布在整个取值范围内。进行整体翼梁结构代理模型样本空间设计时，对结构参数数据进行抽样，样本容量为100，记样本为X。将样本带入整体翼梁结构的参数化模型，模型中裂纹长度选择为1/3H-25mm（止裂筋条下25mm），计算应力强度因子的值，记所有的样本值为Y。

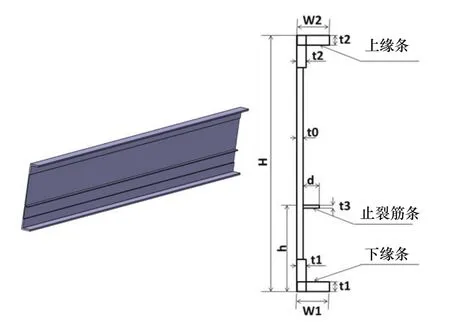
图2　整体翼梁结构截面示参数意图

3.2数据归一化处理

在进行建模预测之前，首先需要对各数据进行归一化处理，将所有具有不同量纲指标的值规范化到[-1，l]区间内以减少训练过程中数值计算的复度，以避免在指标中数值较大的数值控制了整个训练的过程。

首先找出每个参数样本当中的最大值及最小值及样本值的最大最小值，即ymin，然后利用公式(10)进行归一化处理。

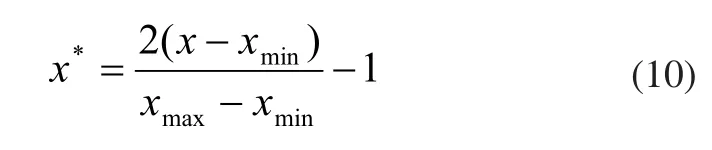
式中，x*为归一化后的值。

对模型的输入数据进行归一化操作后，同时也应该对模型的输出数据进行反归一化操作。反归一化操作和归一化操作是个互逆的过程，作用是还原计算数据恢复实际值，反归一化公式为：

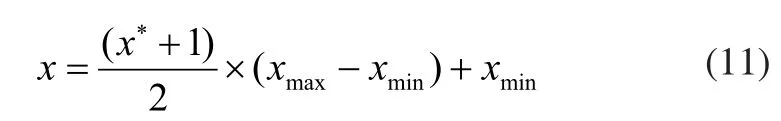
归一化后的样本及样本值分别记为X'，Y'。

3.3代理模型的建立

直接采用安装在MATLAB上的LIBSVM工具箱进行回归模型建立。核函数选择高斯核函数，选择好核函数及相关参数后，调用MATLAB中LIBSVM工具箱的svmtrain函数进行回归训练。

式中，Y表示样本值列向量；X表示样本矩阵；s表示选择支持向量机类型，3表示用支持向量机进行回归训练；t表示选择核函数，2为高斯核函数。a，b，c为支持向量机参数的值。通过运行得到了应力强度因子的代理模型。

在对应力强度因子进行预测时，调用LIBSVM中的svmpredict函数，调用格式如下：

式中，testx表示待预测的样本矩阵；psy表示预测结果列向量；testy表示预测结果估计值，可以给任意一组列向量；mse表示误差，当testy为任意时，该误差无参考价值。

通过数学规划法来对支持向量机参数进行优化，具体步骤如下：

1）确定设计变量，即惩罚函数C、不敏感参数ε以及核参数σ；

2）建立优化目标，优化目标是使支持向量机代理模型的精度最高，具体表示为将n个样本随机分为两组，一组容量为n-10，另一组容量为10，第一组作为训练样本，第二组作为检测样本。用第一组样本建立起来的模型对第二组样本进行预测，将第二组的实际值与预测者的均方误差最小作为优化目标；

3）约束条件，根据文献及经验，选择参数的取值范围，约束条件就为参数取值的上下限；

4）在MATLAB中编写数学规划法程序；

5）运行程序求最优值。

通过数学规划法优化，整体翼梁建立代理模型时，C的值为98965，ε的值为0.0114，σ的值为0.1025。根据优化出来的参数值，带入式(12)，建立代理模型。在以后的应力强度因子预测时，将预测样本带入式(13)即可。

3.4代理模型精度检验

为了检验代理模型的精度，利用拉丁超立方采样方法对整体翼梁结构截面参数进行采样，样本容量为5，如表1所示。

表1　整体翼梁结构检验样本数据

将表1数据带入整体翼梁结构参数化模型，通过ANSYS有限元分析软件计算得到应力强度因子。然后再根据应力强度因子代理模型model1对检验样本进行预测，得到应力强度因子预测值。应力强度因子计算值与预测值如表2所示。

【】【】

表2　应力强度因子计算值与预测值

将结果进行归一化处理，再计算代理模型的均方根误差和相关系数：

均方误差：MSE=0.0503，相关系数：R2=0.9947。

由均方根误差和相关系数可知，应力强度因子代理模型复合精度要求。

4　结论

提出的基于支持向量回归的整体翼梁结构应力强度因子预测技术，其计算结构与有限元分析计算结果吻合且误差较小，满足工程要求。使用该方法可以大大减小计算量，同时也适用于其他结构应力强度因子计算及优化分析。

[1] 翟新康,黄其青,殷之平,等.飞机整体翼梁结构裂纹扩展试验与分析[J].机械强度,2007,29(6):987-991.

[2] 翟新康,黄其青,殷之平,等.飞机整体翼梁结构断裂特性分析研究[J].航空计算技术,2007,(4):71-74.

[3] 黄其青,刘进征,殷之平.整体翼梁结构断裂特性分析方法与研究[J].航空计算技术,2006,(2):114-119.

[4] 翟新康,王新波.飞机整体翼梁止裂筋条结构参数研究[J].飞机工程,2010(4):33-35.

[5] 翟新康.飞机整体翼梁无量纲应力强度因子工程组合计算方法研究[J].飞机工程,2011(1):25-27.

[6] 翟新康,黄其青,殷之平,等.有限元软件在飞机结构打样设计中的应用[J].机械设计与制造,2007,(9):4-6.

[7] 翟新康,李小鹏,张彦军.含裂纹整体翼梁结构剩余强度载荷的估算方法[J].2015年第二届中国航空科学技术大会论文集,国防工业出版社,2015:10-13.

[8] 殷之平,黄其青,傅祥炯.变厚度壁板损伤容限特性研究[J].应用力学学报,2005,(4):665-668.

[9] 黄其青,刘进征,殷之平.整体翼梁结构断裂特性分析方法与研究[J].航空计算技术,2006,(2):114-119.

[10] 翟新康.螺栓群连接中单个螺栓连接失效后的分析评估[J].中国民用航空,2015增刊,(10):296-298.

[11] 焦良,张建华.飞机整体壁板战伤修理研究.航空学报,2000,21(1):64-66.

[12] 傅祥炯.结构疲劳与断裂[M].西安:西北工业大学出版社,1995.

Methodology for resdual strength evaluation of cracked wing beam integrated structure

ZHAI Xin-kang, WANG Bin-tuan, LI Xiao-peng, ZHANG Yan-jun

O346.1

A

1009-0134(2016)02-0142-04

2015-12-03

翟新康（1977 -），男，陕西洋县人，高级工程师，硕士，主要从事飞机结构强度、疲劳与损伤容限设计和试验工作。