数控机床滚动导轨结合面刚度的有限元分析
2016-11-29范晋伟王鸿亮张兰清
范晋伟,王鸿亮,张兰清,袁 帅,纪 实
(北京工业大学 机械工程与应用电子技术学院,北京 100124)
数控机床滚动导轨结合面刚度的有限元分析
范晋伟,王鸿亮,张兰清,袁 帅,纪 实
(北京工业大学 机械工程与应用电子技术学院,北京 100124)
直线滚动导轨是数控机床的重要零部件,其结合面的接触刚度直接影响对数控机床整机动态特性分析。对两种不同直线滚动导轨进行结构简化,运用Pro/E对简化后的滚动导轨进行几何建模,将几何模型转化为IGES中间格式导入ANSYS Workbench有限元分析软件中进行静力学分析。通过对滑块的法向和切向分别施加不同大小的载荷得到变形量的平均值,运用刚度计算公式得到了简化后滑块表面的法向刚度和切向刚度。提出了应用滑块表面刚度来估算结合面接触刚度,并通过反求法进行了验证,最后证明了该方法的正确性。
滚动导轨;结合面;有限元;接触刚度;弹簧刚度;等效
0 引言
机床及各类机械一般都是由零部件组成,而零部件之间相互接触的表面称为结合面(或接触面)。结合面包括固定结合面、半固定结合面和运动结合面。无论是哪种结合面,均是“柔性结合”,即结合面既表现出弹性又有阻尼,既储存能量又消耗能量[1]。许多研究表明,机床中结合面的刚度约占机床总刚度的60%~80%,结合面引起的变形量约占机床总体静变形量的85%~90%[2]。结合面刚度是机床总刚度的重要组成部分,甚至是机床的薄弱环节[3],结合面的变形不仅会影响组成结构的几何关系,甚至会影响机床的加工精度及寿命。在使用有限元软件对机床部件或整机进行动态特性分析时,结合面模型建立的正确与否直接影响分析的结果。
导轨是机床的重要组成部分,其中滑动导轨和滚动导轨是最常见的形式,而导轨与滑块之间的结合面是常见的运动结合面。滚动导轨是在滑动导轨的基础上发展起来的,滚动导轨相对于滑动导轨具有以下优点[4]:1)定位精度高;2)精度保持性好;3)运动速度高;4)工作效率高。随着机床加工精度和工作效率的提高,滚动导轨正在逐渐取代滑动导轨。考虑到滑动导轨结合面刚度的研究理论十分复杂且不够成熟,所得到的公式通用性也不强,目前为止尚未建立完整或通用的结合面动态特性参数数据库[5]。滑动导轨结合面刚度与接触表面粗糙度、所受载荷及移动速度等有关[6],具有强烈的非线性,求解十分复杂。故这里只对滚动导轨结合面的接触刚度进行了研究。随着科学技术的发展,有限元分析分析软件的应用越来越广泛,而且精度越来越高。常见的有限元分析软件有ANSYS、ABAQUS、MSC/NASTRAN等,一般都能进行线性和非线性的结构动力、静力学分析。论文主要采用ANSYS Workbench对滚动导轨法向和切向进行静刚度分析,将测量的变形量采用Excel曲线拟合得到结合面法向刚度和切向刚度。
1 滚动导轨的类型及结合面等效动力学模型
根据滚动导轨的工作状况的不同,常见的类型有三种,分别为[4]:径向载荷型、四方向等载荷型及高载荷型,如图1所示。径向载荷型滚动导轨用于表面承受径向载荷,适用于安装在水平面上,接触角为90°。四方向等载荷型滚动导轨四个方向具有相同承受载荷大小的能力,即四个方向结合面等效刚度相同(下述将对其进行验证),能用于安装在水平和垂直方向,适应能力强,接触角为45°。高载荷型滚动导轨用于对加工要求苛刻的机床,如施加载荷时伴随很大的振动等。

图1 常见滚动导轨类型
考虑到结合面“柔性结合”的特点,在对滚动导轨结合面的研究中,通常对滚动导轨结合面采用弹簧和阻尼器来等效。
等效后系统的动力学方程可统一表示为[7]:

式中:Ma、Mb是滑块和导轨的质量矩阵,Ca、Cb是滑块和导轨阻尼矩阵,Ka、Kb是滑块和导轨的刚度矩阵,Cj、Kj分别是结合间的阻尼矩阵和刚度矩阵,xa、xb是滑块和导轨的坐标向量。其中Cj、Kj又可以分别用结合面间的法向阻尼、切向阻尼以及法向刚度、切向刚度表示为:

2 滚动导轨的几何建模和有限元建模
由图1和图2可知径向载荷型滚动导轨动力学模型可由四方向等载荷型滚动导轨与高载荷型滚动导轨模型联合等效,故本文只对四方向等载荷型滚动导轨及高载荷型滚动导轨进行几何建模和运用ANSYS Workbench进行有限元分析。分析结合面的刚度问题就是求解在载荷的作用下发生的弹性变形量,考虑到直线滚动导轨滚珠的直径大小相同,为减少计算的重复性,可对导轨、滑块和滚珠进行简化[8]。下面分别以某高载荷型滚动导轨和四方向等载荷型滚动导轨为例进行刚度分析。运用Pro/E三维软件进行几何建模,为方便有限元分析,应简化几何模型,去掉小圆孔及倒角等对分析结果影响不大的结构。简化后的几何模型如图2所示。

图2 简化后滚动导轨几何模型
将几何模型转化为IGES中间格式导入ANSYS Workbench有限元分析软件中,使用Static Structural模块进行刚度分析。首先定义材料类型,由资料可知,滑块和导轨材料都是HT300,杨氏模量为1.43×1011N/m2,泊松比0.27,滚珠材料是0Gr18Ni12Mo2Ti,杨氏模量为1.93×1011N/m2,泊松比0.27。滑块与滚珠及导轨与滚珠之间的接触面类型系统默认设置为Bonded,而为接近真实情况这里将接触类型设置为No Separation。在有限元分析中,网格划分的质量好坏直接影响分析的结果,由于ANSYS Workbench具有强大的网格划分功能,在结合有限元网格划分的基本原则[9]的前提下,采用自动网格划分与接触面网格划分同时使用。最后得到的有限元模型如图3所示。导轨一般固定安装在床身或立柱上,故边界条件应定义为导轨底面固定约束。

图3 滚动导轨有限元模型
3 两种不同类型滚动导轨的刚度分析
3.1高载荷型滚动导轨的刚度分析
对高载荷型滚动导轨进行刚度分析,由于要求出结合面法向刚度和切向刚度,故需要在滑块法向和切向分别施加载荷,为了更接近实际受载情况这里所施加的载荷均为面力。为减小误差的影响,采用不同大小的载荷,在法向和切向分别施加100N、200N、300N、400N、500N的压力。为更好地反映出法向接触面和切向接触面的变形量,在滑块的上平面和左平面上均匀的取15的测点,测点的分布情况如图4所示。通过力与滑块表面变形量的关系来估算接触面刚度,各测点的变形量通过坐标探针测量,测量结果如表1和表2所示。
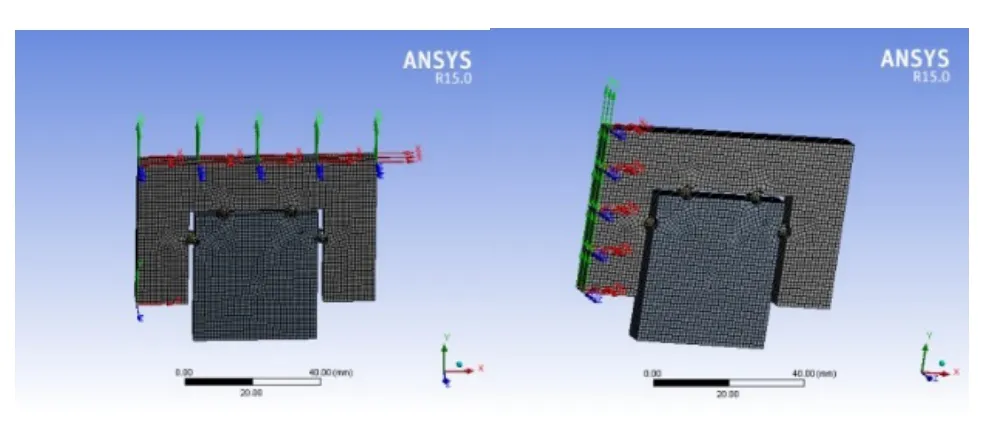
图4 高载荷型滚动导轨测点分布

表1 滑块法向测点的变形量

表2 滑块切向测点的变形量
滑块在100N、200N、300N、400N、500N的压力作用下法向和切向的平均变向量为将压力与法向及切向平均变形量之间的关系通过Excel曲线拟合如图5所示。

图5 载荷与变形量的关系曲线
由刚度计算公式:

可知,拟合曲线的斜率即为刚度,故简化后高载荷型滚动导轨的法向刚度Kn=184191N/mm、切向刚度Kt=72218N/mm。
在结合面的基础参数中,刚度主要影响结构系统的固有频率和振动幅值,阻尼一般不影响系统固有频率而影响振动幅值[10]。考虑到在静力学分析中阻尼的存在并不影响分析的结果,为验证所求刚度的正确性,可在导轨与滑块结合面之间使用弹簧来等效滚珠,并重新进行有限元分析查看法向及切向的变形量。等效弹簧的布置如图6所示,其中法向两根弹簧刚度为92095.5N/mm,切向两根弹簧刚度为36109N/mm。同样,在法向和切向分别施加100N、200N、300N、400N、500N的压力,并在相同位置布置测点探测变形量。有限元分析的过程与上述相同,分析结果如表3和表4所示。

图6 高载荷型滚动导轨等效弹簧分布

表3 等效后滑块测点的法向变形量

表4 等效后滑块测点的切向变形量
同样,采用Excel曲线拟合可得法向刚度Kn=171829N/mm和切向刚度Kt=68006N/mm,与先前所求滑块法向刚度和切向刚度相比误差分别为6.71%和5.83%,均在误差范围内,故简化后该直线滚动导轨结合面法向接触刚度约为184191N/mm,切向接触刚度约为72218N/mm。
3.2四方向等载荷型滚动导轨的刚度分析
四方向等载荷型滚动导轨结合面接触刚度的分析与高载荷型滚动导轨刚度分析的过程相似,同样运用力和滑块表面变形量的关系来估算接触面刚度。分别施加100N、200N、300N、400N、500N的压力于滑块的法向和切向,在滑块的上平面和左平面分别均匀布置15测量点。在不同大小力的作用下可以求出法向平均变形量分别为7.2631×10-4mm、1.4526×10-3mm、2.1789×10-3mm、2.9052×10-3mm、3.6315×10-3mm,切向平均变形量分别为1.5209×10-4mm、3.0418×10-3mm、4.5627×10-3mm、6.0836×10-3mm、7.6171×10-3mm。此时考虑到力和几何关系,计算接触面刚度时力的大小为故法向刚度通过刚度计算公式并结合Excel曲线拟合可得导轨法向结合面接触刚度为194718N/mm。由于该类型导轨的四方向刚度相等,故接触面切向刚度也为194718N/mm。
运用弹簧刚度来等效滚珠刚度并反向验证,等效弹簧的布置如图7所示,6根弹簧刚度均为97359N/mm。在滑块的法向和切向分别施加100N、200N、300N、400N、500N的压力,并在同样的位置布置测点。通过有限元分析的结果可得导轨法向平均变形量分别为7.5235×10-4mm、1.5047×10-3mm、2.2571×10-3mm、3.0094×10-3mm、3.7618×10-3mm,切向平均变形量分别为1.5903×10-3mm、3.1807×10-3mm、4.7711×10-3mm、6.3614×10-3mm、7.9518×10-3mm。通过反求法得到的滚动导轨法向刚度为187973N/mm,与先前所求结合面法向刚度相比误差为3.46%,应用弹簧刚度等效滚珠后滑块切向变形量与等效前相比误差约为4.35%,均在误差范围内,故简化后四方向等载荷型滚动导轨结合面的法向接触刚度和切向接触刚度约为194718N/mm。

图7 四方相等载荷型滚动导轨等效弹簧分布
4 结论
机床整机的动态特性直接影响机床的加工精度、可靠性及寿命等,在进行机床整机动态特性分析时结合面之间的接触刚度模型建立的正确与否十分关键。结合面刚度是机床整机刚度的重要组成部分,尤其是导轨结合面刚度对工件的加工精度影响很大。对滚动导轨建立了等效动力学模型,在动力学模型中结合面之间的接触刚度可以通过接触面的法向刚度和切向刚度来等效。对高载荷型滚动导轨和四方向等载荷型滚动导轨进行了结构简化,应用Pro/E软件进行了几何建模。将几何模型转化为中间格式导入ANSYS Workbench有限元分析软件中进行静力学分析,通过有限元分析求出了导轨滑块的法向刚度和切向刚度。提出了应用导轨滑块的法向刚度和切向刚度来估算导轨结合面之间接触面刚度的理论,并通过反向求解进行了验证,最后证明了所提出的理论是正确的。该理论不仅能用于求解滚动导轨结合面接触刚度,也为求解滚动导轨及机床整机动态特性提供了必要条件。
[1] 廖伯瑜,周新民,尹志宏.现代机械动力学及其工程应用[M].北京:机械工业出版社,2003.
[2] 温淑华.结合面接触特性理论建模及仿真[M].北京:国防工业出版社,2012.
[3] 赵宏林,丁庆新,曾鸣,等.机床结合部特性的理论解析及应用[J].机械工程学报,2008,(12):208-214.
[4] 苗青.数控机床导轨结合面的接触刚度分析[D].洛阳:河南科技大学,2014.
[5] 王维友.机床滑动导轨结合面动态特性参数识别实验研究[D].南京:南京理工大学,2011.
[6] 温淑华,张学良,武美先,等.结合面法向接触刚度分型模型建立与仿真[J].农业机械学报,2009,40(11):197-202.
[7] 朱爽.超高速磨床结构建模的研究[J].沈阳工程学院学报(自然科学版),2014,10(3):275-279.
[8] 刘称意.考虑导轨结合面影响的数控机床动态特性分析及结构优化[D].沈阳:东北大学,2010.
[9] 杜平安.有限元网格划分的基本原则[J].机械设计与制造,2000,(01):34-36.
[10] 崔中,文桂林,陈桂平,等.高速磨床整机动态特性研究[J].中国机械工程,2010,21(7):782-787.
Finite element analysis of NC machine rolling guide joint stiffness
FAN Jin-wei, WANG Hong-liang, ZHANG Lan-qing, YUAN Shuai, JI Shi
TH114;TG659
A
1009-0134(2016)02-0134-05
2015-11-29
国家科技重大专项:中高档国产数控磨床可靠性规模化提升工程(2013ZX04011013);国家自然科学基金项目:数控机床加工缺陷成因的逆向追踪理论与实验研究(51275014)
范晋伟(1965 -),男,河南西平人,教授,博士,研究方向为数控磨床可靠性与超精密加工。
