虚拟裂纹闭合法计算陶瓷材料断裂韧性的有效性研究

王家梁， 马德军， 孙 亮， 肖富君

(1.武警工程大学 装备工程学院，陕西 西安 712086；2.装甲兵工程学院 机械工程系,北京 100072；3.总装备部 南京军事代表局，江苏 南京 210024)



虚拟裂纹闭合法计算陶瓷材料断裂韧性的有效性研究

王家梁1*， 马德军2， 孙 亮2， 肖富君3

(1.武警工程大学 装备工程学院，陕西 西安 712086；2.装甲兵工程学院 机械工程系,北京 100072；3.总装备部 南京军事代表局，江苏 南京 210024)

基于有限元Abaqus软件，采用虚拟裂纹闭合法的基本原理对ISO15732-2003所提SEPB法测试陶瓷材料断裂韧性进行有限元数值计算.以Si3N4、ZrO2、Al2O3、ZTA、SiC五种陶瓷材料SEPB法标准实验为例，分别将虚拟裂纹闭合法计算所得断裂韧性值与标准实验测试值进行对比.结果表明：Si3N4、ZrO2、Al2O3、ZTA、SiC五种陶瓷材料断裂韧性的数值计算值与实验测试值较为一致，其偏差仅分别为1.77%、1.76%、1.82%、1.55%和1.82%.进一步验证了虚拟裂纹闭合法计算断裂韧性值的有效性，同时为该方法的工程应用提供一定的理论基础.

虚拟裂纹闭合法；断裂韧性；单边预裂纹梁法；陶瓷材料

断裂韧性作为材料重要的力学性能参数，一直以来受到国内外研究人员的广泛关注.目前，断裂韧性的计算方法很多，如边界元法[1]、有限差分法[2]以及无网格法[3]等.为利用有限元数值分析软件精确计算材料的断裂韧性值，部分学者提出了单元应力、节点位移外推法、J积分法和虚拟裂纹扩展法等.单元应力、位移外推法要求裂纹尖端具有非常细密的网格，建模过程较为麻烦；J积分计算结果虽然不受网格尺寸影响，但计算过程相对复杂繁琐；虚拟裂纹扩展法需要两步完成，使得计算工作量较大且不利于裂纹扩展问题的研究.针对上述问题，Rybicki和Kanninen于1977年首先提出了虚拟裂纹闭合法(virtual crack closure technique, VCCT)对材料断裂韧性值进行计算[4].由于其计算方法简单、高效，近年来引起了工程界、学术界的广泛关注.由于虚拟裂纹闭合法没有复杂的数学推导过程，其断裂韧性计算结果的有效性一直以来未见相关方面的研究.

本文基于有限元Abaqus软件，采用虚拟裂纹闭合法的基本原理对ISO15732-2003所提SEPB法测试陶瓷材料断裂韧性进行有限元数值计算.以Si3N4、ZrO2、Al2O3、ZTA、SiC五种陶瓷材料SEPB法实验为例，分析比较虚拟裂纹闭合法计算所得断裂韧性值与标准实验测试值的差别，从而对该方法的有效性进行验证.

1 虚拟裂纹闭合法的基本原理

1956年，Irwin提出了应变能释放率(strain energy release rate，SERR)的概念[5].假设一个二维列问题，裂纹长度为a，裂纹体厚度为B，则应变能释放率G定义为产生面积为ΔA的新裂纹面所需要的能量，即

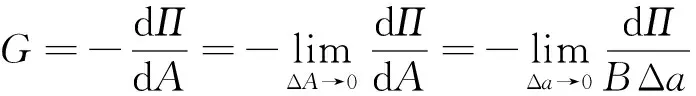
(1)

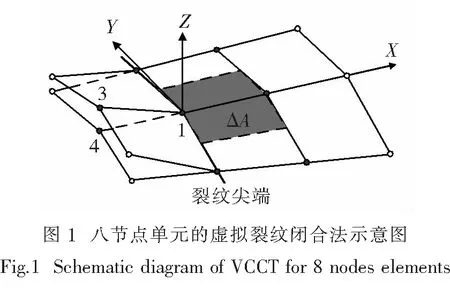
式中：Π=U-W为势能，W为外力功，U为裂纹体应变能.随后，Irwin发现，势能的改变与将裂纹闭合一个扩展增量所需的功等效.因此，Rybicki等人在假设虚拟裂纹尖端后侧的张开位移和实际裂纹尖端后侧的张开位移近似相等的前提下，提出了虚拟裂纹闭合法的基本方法，即计算裂纹尖端某一点的能量释放率G时，需要获取的有限元计算结果为：裂纹尖端处的节点力FZ，裂纹尖端处后侧的节点位移w、裂纹尖端前侧的网格单元面积ΔA.对于八节点线性单元，如图1所示，3节点和4节点位于1节点的后侧，则应变能释放率可表示为

，

(2)

式中：FZ1为节点1沿Z轴的节点力，Δw3,4为节点3和节点4之间的相对位移.由平面应变状态下临界能量释放率GIC和断裂韧性KIC的关系式[6]

(3)

计算得到断裂韧性KIC值.

2 断裂韧性的标准实验研究

表1 SEPB法弯曲试样尺寸参数

国际标准ISO15732-2003[7]因具有较高的理论测试精度和较好的重复性一直以来被广泛用于陶瓷材料的断裂韧性测试中.其基本原理为在弯曲试样表面预制一条长度为l的直通裂纹，通过三点或四点弯曲试验获得裂纹失稳扩展时的最大载荷Pmax，进而根据公式获得所测试样的断裂韧性值，其测试装置示意图如图2所示，弯曲试样示意图如图3所示，尺寸参数见表1.

实验选用氮化硅(Si3N4)、氧化锆(ZrO2)、氧化铝(Al2O3)、氧化锆增韧氧化铝 (ZTA)、碳化硅(SiC)五种陶瓷材料，根据ISO15732-2003的要求制备成40 mm×4 mm×3 mm的标准弯曲试样.所有试样均由中国建筑材料科学研究总院陶瓷科学研究院制备，采用高纯超细粉料通过等静压成型方法制得，其试样密度分别为3.21、6.02、3.95、4.28和3.10 g/cm3.应用MTS-Model 45力学性能试验机对五种陶瓷材料进行三点弯曲测试，如图4所示.其断裂韧性测试结果见表2.

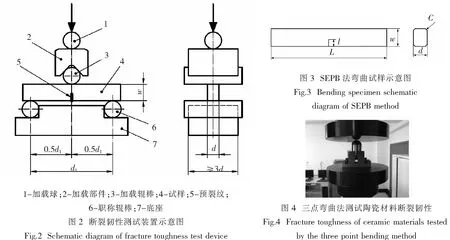
表2 基于ISO15732-2003方法测试得到的五种陶瓷材料断裂韧性值

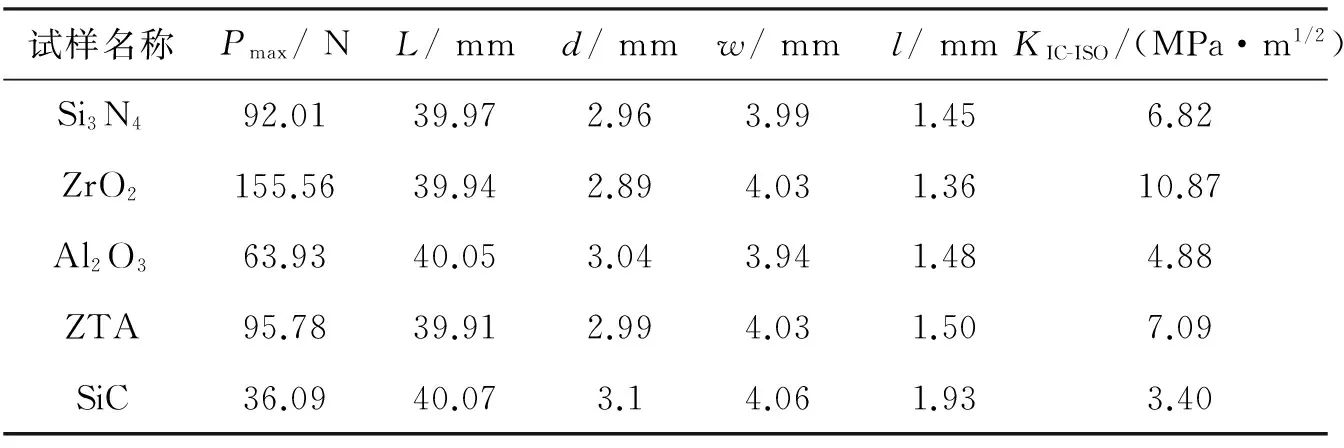
试样名称Pmax/NL/mmd/mmw/mml/mmKIC-ISO/(MPa·m1/2)Si3N492.0139.972.963.991.456.82ZrO2155.5639.942.894.031.3610.87Al2O363.9340.053.043.941.484.88ZTA95.7839.912.994.031.507.09SiC36.0940.073.14.061.933.40

3 数值计算及分析

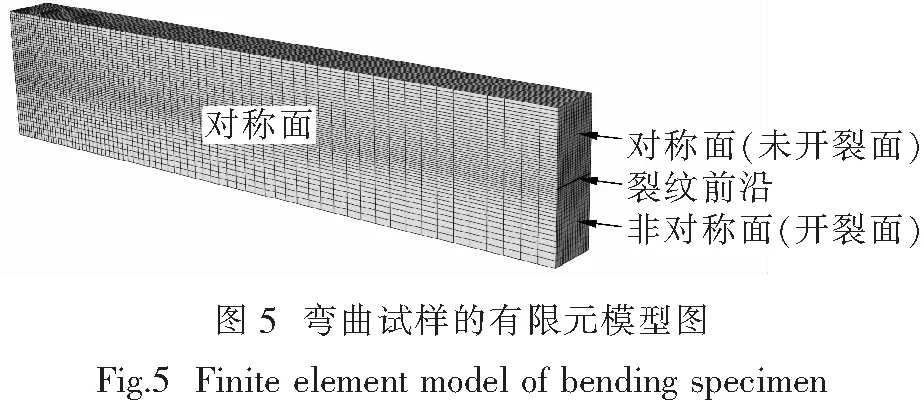
根据上述五种陶瓷材料标准断裂韧性实验所用各弯曲试样尺寸参数，应用商用有限元软件Abaqus，采用与实验相同弯曲试样尺寸进行建模.考虑到弯曲试样的对称性，模型沿裂纹开裂面取试样1/4进行分析.有关三点弯曲测试中滚圆与弯曲试样的接触问题，可直接简化为在弯曲试样的三个接触位置施加与实验条件相同的线载荷进行约束；而对于弯曲试样预裂纹面的建模，可通过定义弯曲试样沿裂纹面的对称性实现，即裂纹面不按对称面设置，未开裂面仍按对称面设置.网格采用C3D8R单元根据核心区(预裂纹尖端)精细，非核心区稀疏的原则进行划分，最终有限元模型图如图5所示.整个有限元数值计算采用非线性大变形理论.滚圆与弯曲试样间的摩擦系数取f=0.15.

根据上述所建有限元数值分析模型，分别采用虚拟裂纹闭合法计算Si3N4、ZrO2、Al2O3、ZTA、SiC五种陶瓷材料在不同预裂纹长度情况下的断裂韧性值，并将虚拟裂纹闭合法计算所得断裂韧性值与标准实验测试值进行比较，结果见表3.其中，有限元模型所涉及的材料参数——弹性模量E和屈服强度σy取值根据文献[8]的方法应用课题组先期研制的高精度宏观仪器化压入仪[9]多次实验测试获得，应变硬化指数n=0(陶瓷为低硬化水平材料).

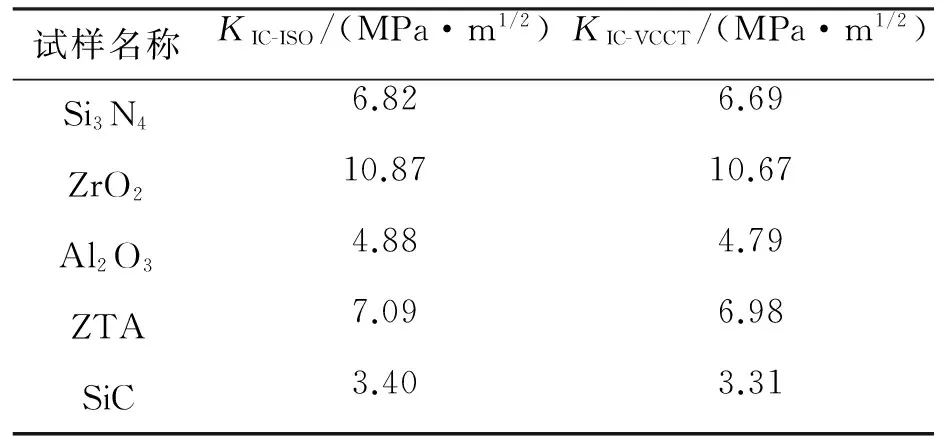
表3 基于虚拟裂纹闭合法计算获得的五种陶瓷材料断裂韧性值

由表3可以看出，基于虚拟裂纹闭合法计算获得的Si3N4、ZrO2、Al2O3、ZTA、SiC五种陶瓷材料断裂韧性值与ISO15732-2003标准实验测试值较为接近，偏差范围较为稳定.同时，考虑到有限元计算过程中使用的五种材料参数系基于仪器化压入测试方法获得，导致材料参数设定与真实参数值存在一定偏差.由此可以说明，采用虚拟裂纹闭合法计算材料的断裂韧性值具有一定的有效性.

4 结 论

基于有限元Abaqus软件，采用虚拟裂纹闭合法的基本原理对ISO15732-2008所提SEPB法测试陶瓷材料断裂韧性进行有限元数值计算.以Si3N4、ZrO2、Al2O3、ZTA、SiC五种陶瓷材料SEPB法实验为例，分别将虚拟裂纹闭合法计算所得断裂韧性值与标准实验测试值进行对比，结果表明：Si3N4、ZrO2、Al2O3、ZTA、SiC五种陶瓷材料断裂韧性的数值计算值与实验测试值较为一致.本文工作进一步验证了虚拟裂纹闭合法计算断裂韧性值的有效性，同时为该方法的工程应用提供一定的理论基础.

[1] 黎在良, 王乘. 高等边界元法[M] . 北京: 科学出版社, 2008.

[2] ZHONG M, ZHANG Y Y. The analysis of dynamicstress intensity factor for semi-circular surface crack using time-domain BEM formulation [J]. Applied Mathematics and Mechanics, 2001, 22(11): 1 344-1 351.

[3] ATLURI S N, SHEN S. The meshless local petrov-galerkin (MLPG) method [M] .Forsyth: Tech Science Press, 2002.

[4] RYBICKI E F, KANNINEN M F.A finite element calculation of stress intensity factors by a modified crack closure integral[J]. Engineering Fracture Mechanics,1977,9(4):931-938.

[5] IRWIN G R. One set of fast crack propagation in high strength steel and aluminum alloys [C]// Sagamore Research Conference Proceedings, 1956, 2:289-305.

[6] 赵建生.断裂力学及断裂物理[M].武汉:华中科技大学出版社,2003.

[7] Fine ceramics (advanced ceramics, advanced technical ceramics)-Test method for fracture toughness of monolithic ceramics at room temperature by single edge precracked beam (SEPB) method：ISO 15732-2003[S].

[8] 郭俊宏.材料弹塑性参数仪器化压入识别方法与测试技术研究[D].北京:装甲兵工程学院, 2013.

[9] 马德军,宋仲康,郭俊宏,等.一种高精度压入仪及金刚石压头压入试样深度的计算方法:CN102288500A[P]. 2011-12-21.

责任编辑：罗 联

Validity Study on Fracture Toughness of Ceramic Materials Calculated by the Virtual Crack Closure Technique

WANGJia-liang1*,MADe-jun2,SUNLiang2,XIAOFu-jun3

(1.Equipment Engineering College,Engineering University of Chinese Armed Police Force,Xi'an 712086； 2.Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072； 3.Nanjing Military Representative Bureau, General Armament Ministry,Nanjing 210024 China)

Based on the finite element analysis software Abaqus, the fracture toughness of ceramic materials determined by the single edge precracked beam(SEPB) method, which was proposed in ISO15732-2003,was calculated by using the virtual crack closure technique (VCCT). Taking SEPB standard test on 5 ceramic materials (Si3N4, ZrO2, Al2O3, ZTA, SiC) for example, the fracture toughness values calculated by VCCT were compared with those derived from SEPB standard tests. The results showed that, the fracture toughness values of 5 ceramic materials calculated by the numerical method and standard test were almost consistent, the deviations are only 1.77%, 1.76%, 1.82%, 1.55% and 1.82%, respectively. This paper further verified the validity of the VCCT on calculating fracture toughness and provided a theoretical basis for the engineering application of VCCT.

virtual crack closure technique; fracture toughness; single edge precracked beam method; ceramic materials

2015-10-05

军内科研计划项目(2014CJ011)

王家梁(1986-)，男，陕西 咸阳人，博士. E-mail:wjllongman@126.com

TQ174.75

A

1000-5900(2016)02-0029-04