基于数据库的部分Ramsey数R(3,l)下界的随机排序构造方法
2016-11-26王世祥
云 微, 张 岚, 王世祥
(长春大学 理学院,吉林 长春 130022)
基于数据库的部分Ramsey数R(3,l)下界的随机排序构造方法
云 微, 张 岚, 王世祥*
(长春大学 理学院,吉林 长春 130022)
利用随机排序的方法给出了Ramsey数R(3,3), R(3,4), R(3,5)和R(3,6)的下界.其中用到了黄金分割方法和数据库动态查询编程.
Ramsey数; 下界; 排序; 黄金分割; 查询
Ramsey数来源于英国数学家F. P. Ramsey于1928年发表的一篇论文[1]. Ramsey数是图论的一个分支,而图是表示系统复杂关系的有效工具,所以人们应用Ramsey数理讨论系统中事务的联系.对Ramsey数的研究涉及到多领域各个方面,特别是在通讯、管理和计算机领域中的应用更为广泛,在计算机领域中网络的设计与规划、大量信息的查询与检索等方面都借助Ramsey数的理论来解决实际问题.
Burr证明了Ramsey数是NP难题[2].计算Ramsey数有多种方法,1992年,Mckay和张克民利用计算机给出了R(3,8)[3],另外还有[4~7]中给出的方法, 这些只是众多研究成果中的一部分,本文主要讨论借助关系型数据库语言,利用动态查询语句解决部分Ramsey数R(3,l)下界的随机排序构造方法.
1 基本概念和思想
(1) 基础概念
n点团: 图中的n个结点组成的完全子图,即其任意两个结点都连接一边.
n独立集: 图中的n个结点,其任意两个结点都不连边.
设R(k,l) 为Ramsey数, 则结点数为R(k,l)-1,既不包含k点团也不包含l独立集的图称为Ramsey(k,l)图, 简记为R0(k,l) , 其结点个数记为m(k,l)[8].
(2) 基本思想
下面主要以图R0(3, 5)为例, 说明数据结构和模块算法.
图R0(3, 5) 无3点团(可称红3)和5独立集(可称蓝5), 其m(3, 5) =13. 此图的预备图(可变化)记为T(3, 5), 含13个结点, 相应的表为tabls0.
当所有边未连接时, T(3, 5)为13独立集, 当连接边(1,2)(称为选定边)时, T(3, 5)含2个12独立集:
1,3,4,5,6,7,8,9,10,11,12,13; 2,3,4,5,6,7,8,9,10,11,12,13.
当再选定边(3,4)时, T(3, 5)含4个11独立集:
1,3,5,6,7,8,9,10,11,12,13; 1,4,5,6,7,8,9,10,11,12,13;
2,3,5,6,7,8,9,10,11,12,13; 2,4,5,6,7,8,9,10,11,12,13.
继续下去,当一共选定6个边(1,2),(3,4),(5,6),…,(11,12)后(如果对m(3, 4) =8,则选到(1,2),(3.4),…,(7,8)),产生64个7独立集.
如果继续选边,按独立集分类,会产生3个层次(记为变量cshu=3):7独立集, 6独立集和5独立集(小于5的独立集都删除了,删除的独立集与别的独立集无关),每种独立集含若干个元.
主要数据表有3个:
tabls0,字段及数据类型为:id int, e varchar(100), count1 int, bz int.本表的数据是对应图T(3, 5)产生的独立集. 比如, 初始的13独立集在表中为1111111111111. 第1次选定边(1,2)时, 对应两个12独立集.表tabls0有1011111111111 和 0111111111111.如5独立集13579,在表中是长度为13的01字符串: 1010101010000. 含1的个数count1=5.
tabij, 主要字段为: bh, id, ei, ej, ci, cj, count0, bz, c1,…, c5. 它们的数据类型都是 int.
本表存放可选边的信息. 为简洁计, 去掉对称的, 这些边为(1,2),(1,3),…,(1,13), (2,3),…,(2,13),…, (12,13),呈三角形. 存放于(ei, ej)中. ci 和 cj 是记录点 ei 和 ej 的个数, 这个数必须小于 m(k,l) 中的l, 否则会出现红3. 标志 bz 取值为0或1. 0表示可选边,1表示已选边或停选边(为不形成红3而不能选的边),c1至c5是为排序用的, count0 为诸 ci 之和.
tabcanshu2, 类型为 int 的有: bh, id, cshu, ydian, count1, bz, 类型为 varchar(300)的有 ord, ord1~ord6.本表存放一些用到的参数, ord 等是排序的字符串表达式.
子模块主要有4个:
prodate1(m(k,l)): 根据m(k,l), 用双重循环生成表tabij中的数据.
profenlie(l,i,j): 根据选定边(i,j),将表tabls0中既含i又含j的独立集分裂为两个低一层的只含i和只含j的独立集.方法是将既含i又含j的所有独立集复制为两批,再将其中一批的j位改为0,另一批的i位改为0. 然后将count1小于l的所有独立集删除. 其中l即为m(k,l)中的l.
protongji (tablename, m(k,l)): 首先确定表tabls0中独立集的层次cshu, 如cshu=3, 即有三种独立集, 根据cshu从表tabcanshu2取得排序字符串(cshu不同, 则要点ydian不同, 此ydian是根据黄金分割确定的排序的首位). 对表tabij中的每个bz=0的元(ei , ej), 统计出表tabls0各cshu中包含的独立集的个数(既含ei又含ej的独立集的个数),分别放入该元的c1, c2, c3中, 以备下面排序用. 注意, 当m(k,l)=17,对cshu=3且2层与3层独立集个数之和小于1层独立集个数乘0.618,则排序为c1, c2, c3.
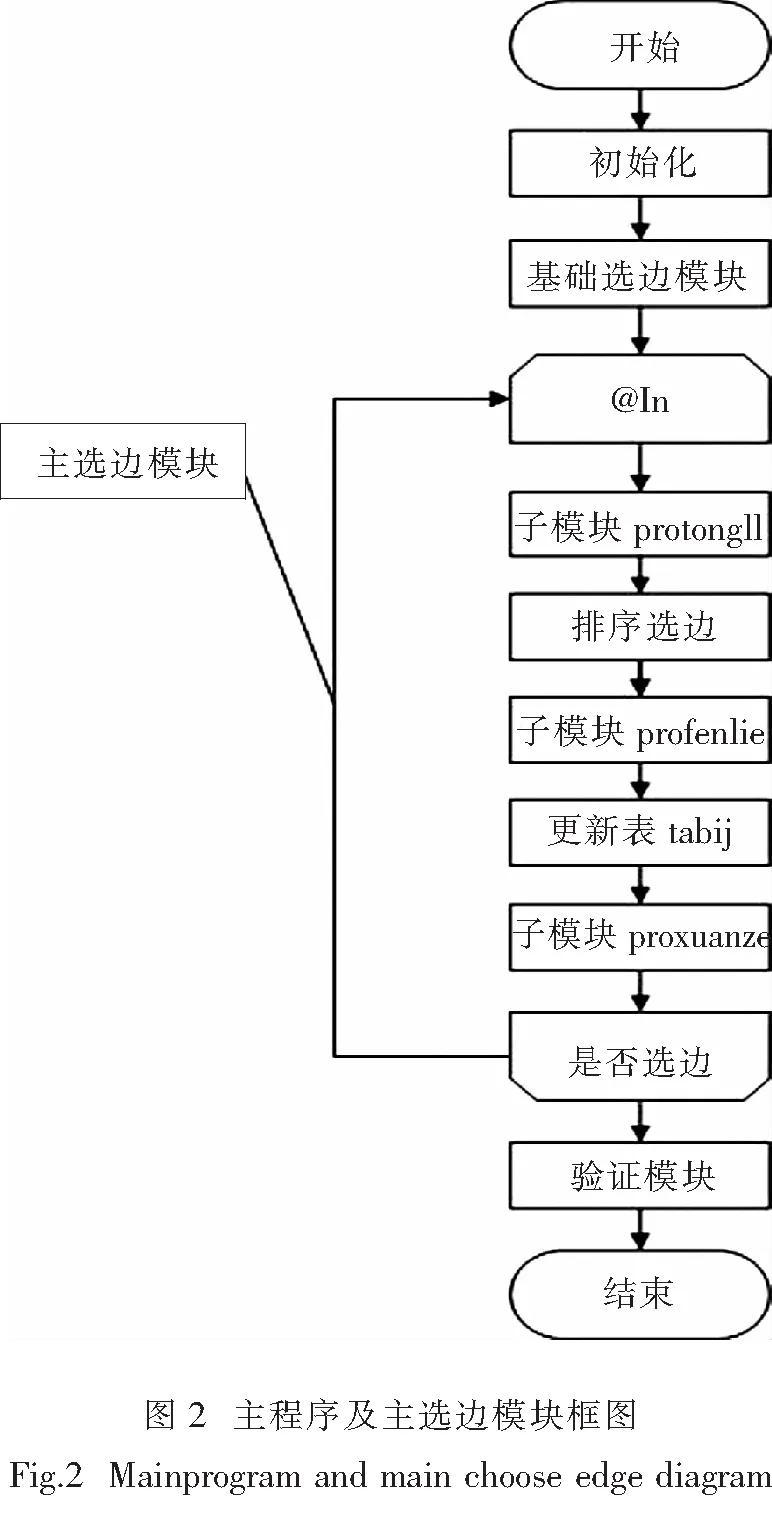
proxuanze(m(k,l), ei , ej, bz): 根据即时选定边(ei , ej)和已有选定边确定停选边(下一步不能选的边). 设(y, z) 为即时选定边, (w, y) 或 (w, z) 等为已有选定边. 则第3边为停选边. 按以下四种连接方式(注意: 按表 tabij 关于可选边的设定, 边 (y, z) 应满足y 有以下种可能情况:(1)(w, z); (2)(w, z),( z, w); (3)(y, w),(w, y); (4)(y, w). 它们就是停选边. 这样使得停选边的确定有了明确的依据. 主程序promain由3个模块组成.分别为基础选边模块、主选边模块和验证模块. 主程序设有3个参数m(k,l),k,l. 首先由子模块prodate1生成所有可选边的表tabij, 也要作一些其他初始化的工作. 基础选边模块是根据m(k,l)选定边: 当m(k,l)为偶数时,选定(1,2),(3,4),(5,6),…,( m(k,l)-1, m(k,l)),若m(k,l)为奇数则最后选定到(m(k,l)-2, m(k,l)-1). 这些边互不相连显然不会形成红3,故不需检验. 本模块是一个循环,In从1到con(根据参数m(k,l) 从表tabcanshu1中列con取值),循环体中,取 ei = In, ej = In+1, 对于选定边(ei , ej), 更新表tabij中的bz=1, 并将ci和cj加1. 根据(ei , ej),使用子模块profenlie分裂独立集. 为观察数据变化, 使用子模块protongji作一下统计. 主程序程序框图及主选边模块框图如图2. 主选边模块是一个循环.其主要步骤是: 先运行protongji对表tabls0作统计.排序选边就是一条SQL语句: select top(1) @ei=ei,@ej=ej from tabij where bz=0 order by count0 desc,c1 desc,c2 desc,c3 desc,c4 desc,c5 desc,ei,ej,ci,cj 它的排序是固定的, 不同的排序变化在protongji里处理. 选定边后执行profenlie, 并更新表tabij (参见基础选边模块), 如果表tabij中边满足bz=0 但对于m(k,l) 中的l有ci =l或 cj =l时就将其bz改为1(也成为停选点). 最后根据选定边运行proxuanze以确定下一步的停选边或说确定下一步的可选边. 验证模块可以单独执行. 这个模块由两部分组成: 第一部分是,验证由选定边的集合确定的图R0(3,5)确实不含5独立集. 方法是该集合可以消除所有5独立集(注意, 7独立集由7个6独立集组成, 6独立集由6个5独立集组成).这需要用到表tabls1, 它包含所有长度为13的5独立集,共有1 287个元.第二部分是,验证图R0(3, 5)不含3点团,只要对选定边的集合的每个元 (x, y), 如果有 (y, z), 则判定没有(x, z) 就行了, 这可以用一个双重循环实现. (1) 基础数据表 R0(k,l)(3,3)(3,4)(3,5)(3,6)(3,7)(3,8)m(k,l)5813172227可选边数102878136231321选定边数51226426694tabls1元10701287123761705442277660 (2) 排序取值数据 cshun1234567n×0.6180.6181.2361.8542.4323.0903.7084.329ydian1122344m(k,l)5,813172227 (3) 排序详细数据 cshu34序号(0)(1)(2)(3)(4)(5)(1)(2)(3)(4)(5)1C1C2C1+C2C2C2C2C2C2+C3C2C2C32C2C1C2C2C1C1C3C2C2C3C23C3C3C3C3C3C2C1C3C3C4C14C4C4C4C4C1C4 (4) 图R0(3, 5)的一个可行边集 (1, 2), ( 9, 10), ( 5, 7), (2, 12), ( 2, 4), (2, 8), (8, 10), (3, 4), (11, 12), ( 9, 11), (4, 10), (5, 12), (3, 7), (12, 13), (5, 6), ( 1, 13), ( 6, 8), (3, 11), ( 1, 6), (4, 5), (7, 8), ( 3, 13), (10, 13), ( 1, 9), ( 7, 9), (6, 11). 给出上面边集, 在个人电脑上运行时间0.656 s. 给出图R0(3,6)的可行边集, 需2.114 s. Ramsey数的原理在网络通信的规划和设计中应用广泛.通信网络中的中继器和各种中间设备抽象成结点,而结点之间的通信链路抽象成线,这样就得到一个图.为了避免在通信中因为某个结点或某条线路的问题导致通信中断,要设计任意两个结点之间至少有一条畅通的线路.假设有n个结点的网络为了保证通信的畅通,任意两点之间添加一条线路需要n*(n-1)/2条,但是如此之多的线路会增加成本以及给后期维护带来问题,如何减少结点之间的线路还要保证通信的畅通,解决这个问题可以用Ramsey数的原理,所以我们用数据的查询语句解决部分Ramsey数R(3,l)下界的随机排序构造方法十分有必要. [1] RAMSEY F P. On a problem of formal logic [J]. Proc Lond Math Soc, 1930,30:264-286. [2] BURR S A. Determining generalized Ramsey numbers is NP hard [J]. Ars Combinatoria, 1984, 17:21-25. [3] MCKAY, ZHANG K M. The value of the Ramsey number R(3,8) [J]. Journal of Graph Theory,1992, 16(1):99-105. [4] 苏文龙,罗海鹏,吴康.素数阶循环图与Ramsey数下界[J]. 梧州学院学报, 2005, 15(1):1-4. [5] 罗海鹏,苏文龙, 许晓东,等.4个经典Ramsey数R(3,q)的新下界[J].广西科学,2006,13(3): 161-163. [6] 陈红,吴康,许晓东,等.9个经典 Ramsey 数 R(3,t)的新下界[J]. 数学杂志, 2011, 31(3): 582-586. [7] 刘恩来.一种求解Ramsey数的计算机算法[D].扬州:扬州大学,2014. [8] 《现代应用数学手册》编委会. 现代应用数学手册(离散数学卷) [M].北京:清华大学出版社,2002. [9] NIELSEN P. MICROSOFT SQL Server 2000 宝典[M].刘瑞,陈微,闫继忠,等译.北京:中国铁道出版社,2004. 责任编辑:龙顺潮 Random Sort Constructor Section Ramsey Number R (3,l) Lower Bound YUNWei,ZHANGLan,WANGShi-xiang* (College of Science,Changchun University, Changchun 130022 China) In this paper, the method gives a randomly ordered Ramsey numbers R (3,3), R (3,4),R(3,5) and R (3,6) of the lower bound. It uses the golden section method and database programming dynamic query. Ramsey number;lower bound; sort; golden section; query 2016-03-21 吉林省教育厅项目(2016285) 王世祥(1956-),男,吉林 辉南人,教授.E-mail:467342609@qq.com O157.5;TP311.12 A 1000-5900(2016)02-0005-04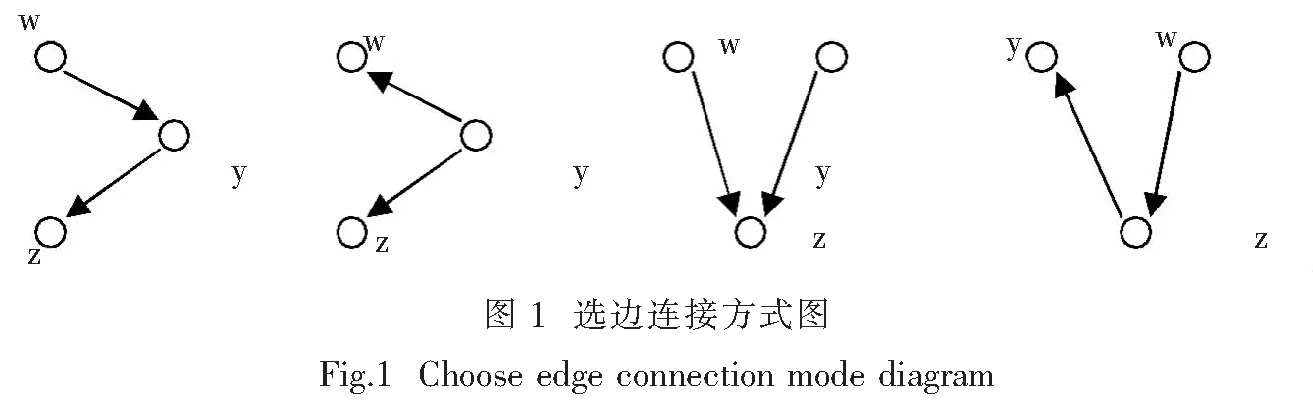
2 主程序算法
3 数据与结论