探寻等差数列前n项和公式的“自然”之路

☉浙江省象山县第二中学　郑洲

探寻等差数列前n项和公式的“自然”之路

☉浙江省象山县第二中学郑洲

中学数学绝大多数内容是人类在长期实践与反思中经过千锤百炼的数学精华和基础，其中数学概念、思想、方法的起源与发展过程都是自然的.每一种数学概念、思想与方法，从它的产生背景、形成过程及应用看，都是水到渠成、浑然天成的，不仅合情合理，而且很有人情味.［1］若在教学中，教师照本宣科，直接抛出数学概念、思想方法，就像魔术师“从帽子中突然掏出一个兔子”似的，这将不利于学生感受到数学的存在及领悟到数学的真谛，从而很难实现思维过程的“理性重建”.因此，教师在数学教学中必须顺应自然法则，遵循学生身心发展规律和基本特征，构建清新自然的数学课堂，使数学知识的形成发展和学生认知数学的思维过程有机地融合在一起，让学生在感受数学自然、亲切的同时，产生“看个究竟”的冲动，兴趣盎然地投入到数学学习中去.

一、引入和实际脱离怎能自然

众所周知，在“等差数列的前n项和公式”的推导中，教材（人教A版）给出的求和公式的推导过程是先从高斯求“1+2+3+…+100=？”的方法引入等差数列求和问题，然后利用“倒序相加”法推导一般的等差数列求和公式.这样的安排体现了两方面的意图：一是启发学生掌握从特殊到一般的数学研究方法，发展探究事物的能力，发展理性思维，提高思维品质；二是让学生感受成功的喜悦，培养学生的自信，逐步形成勇于探索的学习方式.但高斯算法就是把1到100这100个数两两配对后分成50组，且每组两个数之和都为101，从而迅速得出结果是5050.这种算法的本质应该是“配对求和”，而等差数列求和公式的推导最终使用的是“倒序相加”，这两种方法之间缺乏必然的联系，在实际教学中，学生很难从“配对求和”中自然想到“倒序相加”.为了能够顺利完成公式推导教学，很多教师的做法是在引入高斯求和后直接向学生抛出“倒序相加法”.但这样的“告知”无疑脱离了学生的思维发展实际，公式的探究过程就异化为灌输的过程.从接受式学习的角度来说，学生对“倒序相加”是非常容易理解和接受的.但从发现式（或者说探究式）学习的角度来看，教材的设计意图就没能实现，用高斯算法引入的思维价值没有恰当地发挥作用，只是为了引入而引入，更是违背了“数学是自然的”教学宗旨.［2］因此，我们不禁要思考，该如何设计一条顺乎自然，顺应学生认知规律的等差数列求和公式的探究过程.

二、因势利导，顺其自然

既然高斯求和无法自然地过渡到“倒序相加”，那么我们在教学时就没必要走“倒序相加”的路，顺着高斯求和的思维轨迹学生会想出什么方法呢？实践证明，多数学生在了解高斯的“配对求和”后，自然会想到用“配对求和”的方法求等差数列“1+2+3+…+n=”的和，无非在配对的过程中考虑n的奇偶性，最终他们发现不论n是奇还是偶，“1+2+3+…+n=的推导思路，很容易推导出等差数列的求和公式.由此可见，“配对求和”的思想不仅能够顺利解决等差数列求和问题，而且比起“倒序相加”学生能够自然想到的，更加难能可贵.

三、归纳猜想，延续自然

我们知道知识的学习具有连续性，前面所学的知识往往对后续知识的学习具有引导作用.学生在前面推导等差数列通项公式时，教材采用的是归纳法，学生对此应该印象颇深.如果我们能够延续前面的思路推导等差数列求和公式是不是会更显自然，更加容易被学生接受.

先让学生计算S1，S2，S3，S4的值，学生容易求得S1=a1，S2=2a1+d，S3=3a1+3d，S4=4a1+6d，由此可以初步归纳出Sn= na1+f（n）d，那么问题就归结为对公差d前面系数的确定.然后，教师引导学生把d前面的数字进行拆分就很容易猜测出其中的规律.S2=2a1+1×d，S3=3a1+（1+2）d，S4=4a1+（1+2+3）d，依次类推可以归纳出Sn=na1+（1+2+3+…+n－1）d，最后问题就归结为对“1+2+3+…+n－1”的求和.［3］处理这个求和问题可以利用高斯求和，也可以引入倒序相加.当然，用归纳猜想的方法推导求和公式或许存在着严密性的不足，但这是学生借助“配对求和”自然想到的可贵之处.让学生从已有的知识出发进行探索，尝试了原有方法解决的可能性，并在此基础上进行再探索研究，所学知识进行了一次新的整理，从中发现出一些有价值的东西，并应用于新的知识的探求，因此探究过程更加自然流畅.

四、数阵助力，回归自然

数形结合思想是高中数学最基本的数学思想之一.从具体图形入手，通过直观感知，观察分析，最后获得解决问题的灵感是学生最常用的探究方式，当然也是最自然的学习方式.教师先启发学生把数列各项用基本量a1和d表示出来，然后把它们排列成如图1所示的数阵，则要求数列的和只需求出a1和d的个数即可.易得a1的个数为n，d的排列图形呈现出三角形的形状，直接利用三角形不容易获得d的个数.接下来，教师就可以引导学生通过“补形”的方式，构造出如图2所示的数阵.如此一来，d的排列图形转化成了矩形，只需求出矩形中d的个数即可，易求d的个数为d.不仅如此，这种“补形”的思想其实也蕴含着“倒序相加”的“影子”.我们前面提到由高斯算法学生很难自然想到“倒序相加”，真是“无意带将花一朵，却挑蝴蝶下山来”，现在这个数阵就架起了跨越这一思维障碍的桥梁，实现了思维的自然回归.

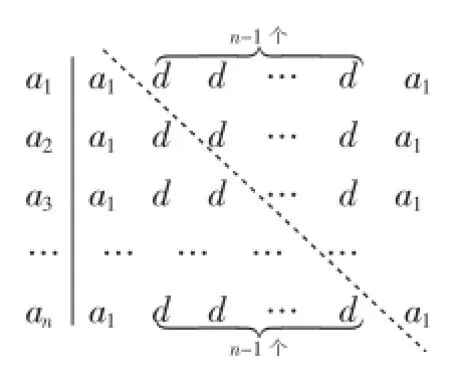
图2　

图1　

至此，笔者不由的想起教材（人教A版）寄语中有关“数学是自然的”描述：“数学概念、数学方法、数学思想的起源与发展都是自然的.如果有人感到某个概念不自然，是强加于人的，那么只要想一下它的背景，它的形成过程，它的应用，以及它与其他概念的联系，你就会发现它实际上是水到渠成、浑然天成的产物，不仅合情合理，甚至很有人情味.这将有助于大家的学习.”尽管“条条大路通罗马”，但我们要尽量选择“自然”之路.

1.王峰．概念教学要崇尚自然［J］．中学数学研究，2012（5）．

2.陈朝晖．“等差数列的前n项和公式推导”的商榷［J］．数学通报，2007（5）．

3.冯寅．研究性学习的个案分析——等差数列前n项和公式的教学实录［J］．数学教学研究，2002（12）．F