磁性液体阻尼减振器的实验研究
2016-11-23朱姗姗李德才崔红超
朱姗姗, 李德才, 崔红超
(1.北京交通大学 机械与电子控制工程学院,北京 100044; 2.北京工业职业技术学院,北京 100042)
磁性液体阻尼减振器的实验研究
朱姗姗1,2, 李德才1, 崔红超1
(1.北京交通大学 机械与电子控制工程学院,北京 100044; 2.北京工业职业技术学院,北京 100042)
基于二阶浮力原理,着重研究了磁性液体阻尼减振器不同壳体内壁、不同端盖锥角对减振器减振性能的影响。通过试验分析得知粗糙内壁的壳体减振性能优于光滑内壁的壳体;在一定范围内,端盖锥角大的减振器减振性能比端盖锥角小的减振器减振性能好。
磁性液体;壳体;端盖锥角;减振性能
在理想状态下,长期载人空间站在轨期间处于失重状态,有很多因素引起振动,而且在失重状态与真空环境的双重影响下,振动会对空间站的运行产生严重影响。在特殊的工作环境中,对减振设备也提出了更高的要求。首先空间站的减振器要求结构简单、体积小、质量轻且可靠性高。其次,因为航天器中较长物体(如太阳能帆板、卫星天线等)的局部振动具有频率低、位移小、加速度小的特征,所以要求减振器对惯性力非常敏感。
普通减振器结构复杂,很难满足空间环境的特殊要求,而基于磁性液体二阶浮力原理的磁性液体阻尼减振器在很大程度上满足了空间环境的特殊要求。磁性液体是一种由包覆有表面活性剂的纳米铁磁性或亚铁磁性颗粒分散于液态载液中形成的稳定的胶态悬浮液。在磁性液体研究早期,美国NASA宇航局最先开始了对磁性液体阻尼减振的研究,随后磁性液体阻尼器和调谐磁性液体阻尼器等多种阻尼器成为科研人员的研究热点[1]。
1 磁性液体阻尼减振器的结构及其工作原理
磁性液体是一种新型的功能材料,它既具有液体的流动性又具有固体磁性材料的磁性,在磁场的作用下,呈现出普通液体所没有的特性。一方面,磁微粒子在基载液中不停地做布朗运动,即使在重力、磁力、离心力同时作用下也不会发生固液分离;另一方面磁性液体具有超顺磁性,在外加磁场下,会出现相应的磁特性、黏滞性、流变性和双折射性等独特的性能。基于磁性液体二阶浮力原理的磁性液体阻尼减振器既不需要外加磁场或任何激励、减振性能稳定,并且寿命长、无泄漏[2]。磁性液体二阶浮力原理是指磁性液体可以将浸在其中的比重比磁性液体大的永久磁铁悬浮起来。利用磁性液体的双重特性以及永久磁铁在磁性液体中自悬浮的性质,通过永久磁铁在磁性液体中做往复运动需要吸能而达到消能减振的效果,设计了磁性液体阻尼减振实验台,减振器的减振原理如图1所示,对磁性液体阻尼减振器减振性能进行研究[3]。

图1 磁性液体阻尼减振原理Fig.1 The theory of magnetic fluid damper
磁性液体阻尼减振器由非磁性外壳、圆柱形永久磁铁和磁性液体组成。当永久磁铁浸没于磁性液体中时,在垂直方向上,永磁体受到自身重力Fg的作用而向下运动,同时还受到磁性液体对它产生的方向向上的浮力Ff和阻力Fr作用;当永磁体接近壳体时,由于壳体为非磁性的,永磁体下方的磁力线被压缩,在永磁体下方产生比上方更大的磁场强度梯度,从而在永磁体上下表面产生一个向上的磁压力Fm与重力平衡,使永磁体悬浮在磁性液体中。在整个运动过程中,力的平衡方程为:
F=Fg-Fm-Ff-Fr
式中:F为永磁体运动过程中所受的合力。当永磁体达到自悬浮时,Fr=0,永磁体只受到Fg,Ff和Fm的作用,此时力的平衡方程为:
Fg=Ff+Fm
理想状态下,空间站在轨期间处于失重状态,则力的平衡方程为:
Ff+Fm=0
根据这种自悬浮的原理,永磁体便能稳定的悬浮在磁性液体中。当减振器受到外界的冲击时,永磁体会偏离平衡位置向壳体的一侧移动,压缩磁力线,从而产生一个指向平衡位置方向的磁压力,使永磁体往复运动,直至稳定在平衡位置。这样永磁体在运动过程中带动磁性液体运动做功而吸收能量,最终达到消能减振的效果[4]。
2 磁性液体阻尼减振实验
2.1 磁性液体选择
由于氟碳化合物基磁性液体具有良好的稳定性,耐酸碱性和抗辐射性。本试验选用购买的黏度为232 mPa·s 的氟碳化合物基磁性液体[5]。
2.2 永久磁铁的选择
由于铷铁硼(NdFeB)属第三代稀土永磁材料,是当代磁性最强、性能最好的永磁材料。在磁性液体阻尼减振器中使用烧结钕铁硼永久磁铁[6]。经过特殊处理的永久磁铁,其最高工作温度可达200℃。而且前期的科研人员在太空的射线收集试验中也是使用了铷铁硼,证明铷铁硼能够应用于宇宙空间环境中的宇航设备上[7]。
由于试验是利用永久磁铁在N-S两极所吸附的磁性液体与减振器的上下两个面的压力来产生速度梯度,进而产生摩擦力,消耗能量。圆柱形永久磁铁吸附磁性液体时,圆周面和上下两个面的磁性液体也比较饱满,由此在试验过程中产生的压力大,使得磁性液体的速度梯度大,减振效果更加明显。由此根据减振器的大小选择两个铷铁硼φ30 mm×10 mm的永久磁铁叠加试验。
2.3 磁性液体阻尼减振器的设计
2.3.1 黏性液体管内流动沿程损失与局部损失理论推导
根据流体力学中黏性流体管内流动的总流Bernoulli方程:

hw=∑hf+∑hj
即黏性流体在管道中流动时,产生的能量损失可分为hf和hj两类,其中hf为单位重力流体的沿程损失,hj为单位重力流体的局部损失。
而l为流程长度或管道长度;d为管道内径;λ为沿程损失系数,无量纲。
并且ζ为局部损失系数,无量纲。
2 320 反算出Δ,得出工业管道的当量粗糙度。之所以是当量粗糙度,是因为实际管道的粗糙凸出程度是不均匀的,将反算出的均匀的粗糙度代替一个不均匀的粗糙度,不是实际的粗糙度[8]。 2.3.2 减振器结构设计 本试验采用不导磁的ABS材料加工的减振器外壳进行减振试验。为了得到更好的减振效果,将减振器外壳的端盖的内表面加工为锥形,如图2所示。以粗糙度测量仪测量端盖内表面Ra值分布在[3.84 μm,46.72 μm]范围内。当永久磁铁偏离中心时,端盖的锥形内表面会作用于磁性液体一个回复力,不同端盖锥角时磁性液体的受力状态如图3所示。端盖锥角作用于磁性液体的回复力可以保证在失重环境下永久磁铁始终处于减振器的中心位置。 图2 磁性液体阻尼减振器结构简图Fig.2 The structure of magnetic fluid damper 图3 磁性液体在不同端盖锥角下受力状态Fig.3 The forced state of magnetic fluid in different cone angle 为了验证不同端盖锥度对减振性能的影响,端盖采用不同角度,分别为175°、170°。 本设计选用内壁为规则圆柱面为磁性液体的壳体,没有弯管、孔板、渐放管和渐缩管结构,因此先不考虑磁性液体壳体内的局部损失。根据黏性液体管内流动沿程损失与局部损失的理论推导,hf∝λ∝Δ,前人在试验中均选择光滑的金属或者非金属作为阻尼减振器的磁性液体的壳体,本设计中选择壳体内表面极其粗糙的由3D打印成型的ABS壳体作为磁性液体阻尼减振器的外壳,与光滑内壁的外壳试验对比减振性能,壳体内壁均为φ60 mm×25 mm。 2.4 振动系统的力学模型 对于黄铜板,以黄铜板的集中质量代替分布质量来建模;针对参数化模型不能直接反映阻尼器逆向动态特性、非参数化建模需大量试验数据问题[9],结合两者则黄铜板与阻尼减振器两个质量块的振动微分方程为: 假设其解的形式为: xj(t)=Xjeiωt,j=1,2 则 X1= 引入以下符号: μ=m2/m1 X1/δst= X2/δst= 如果阻尼为零(即c2=ζ=0),则共振发生在系统的两个无阻尼共振频率处,共振将导致X1=∞,因此当c2=0和c2=∞时,X1的峰值为无穷大,所以在两个极限之间必定存在某个阻尼值使X1的峰值最小。将ζ=0和ζ=∞两种临界情况代入式 X1/δst= 并令两者相等,可以确定这两点: ga=ωa/ω,gb=ωb/ω,分别代入式X1/δst= 即: 基于试验要求振动频率低、振幅小的特点,振动装置选用黄铜板。该实验采用自由振动实验,以初始位移作为激励条件,以消振时间长短作为反映阻尼器性能的指标。采用其一端固定, 另一端自由端安装磁性 液体阻尼减振器。为了得到不同频率的振动,选取不同长度的铜板进行试验,铜板的宽度和厚度分别为50 mm 和5 mm。铜板长度为0.5 m~2.0 m,铜板悬臂梁频率范围为0.75 Hz~5.80 Hz的振动,悬臂梁提供振幅范围10 mm~20 mm。 3.1 试验结果 试验装置采用压电式加速度传感器(内部集成了信号放大器),数据采集系统、分析处理软件DASP和计算机组成。实物连接如图3所示,试验数据分别如表1和表2所示。其中图4中所示有两个传感器信号,铜板下端的传感器位于铜板振幅最大处,实验中采集的数据来源于铜板下端的传感器信号。 图4 振动分析试验装置Fig.4 The device of analysis on vibration 铜板长度/m0.51.01.52.0铜板自由端初始偏移量/mm1020102010201020端盖锥度/(°)10°5°10°5°10°5°10°5°10°5°10°5°10°5°10°5°消振时间/s3.026.139.0813.735.258.4512.0418.577.579.2314.8919.648.9410.6116.8221.27 表2 磁性液体阻尼减振粗糙内壁壳体试验研究 3.2 试验分析 试验中首先考虑磁性液体阻尼减振器的内表面粗糙度相对于较光滑内表面减振器的减振性能。黏性流体在管道中流动时,产生的能量损失可分为hf和hj两类,即hw=∑hf+∑hj。从试验数据得知,在相同铜板长度、相同铜板自由端初始偏移量、相同的端盖锥度的试验中,粗糙内表面的减振器的消振时间明显较光滑内表面的消振时间短。 试验中,采用同样的振动激励时,不同长度的黄铜板在减振中表现的消振时间不同。由于 不同长度的黄铜板与减振器的质量比不一致,减振器的固有频率ωa和主质量的固有频率ωn比不一致,所表现的减振性能也不一致。 试验中采用长度相同的黄铜板和相同的振动激励时,不同端盖锥角的减振器的减振时间也不一致。试验中采用的减振器的端盖锥角分别是5°和10°,在本试验范围内,采用10°的端盖锥角比采用5°的端盖锥角减振时间短。根据图3所示,不同端盖锥角对磁性液体的回弹力不同。在相同的振动状态下,在一定范围内,端盖锥角越大,端盖对磁性液体沿水平方向的分力,也即能够使磁性液体回弹的力越大。 (1) 利用二阶浮力原理设计的磁性液体阻尼减振器,选用不同壳体,其内表面粗糙度不同,对减振时间有明显的影响; (3) 磁性液体阻尼减振器的端盖锥度对减振性能也有一定的影响,在一定范围内,端盖锥度较大的减振器比端盖角度较小的减振器减振性能好。 [1] BASHTOVOI V G, KABACHNIKOV D N, KOLOBOV A T. Research of the dynamics of a magnetic fluid dynamic absorber[J]. Journal of Magnetism and Magnetic Materials. 2002, 252:312-314. [2] QIAN Jiguo, YANG Zhiyi. Characteristics of a magnetic fluid seal and its motion in an axial variable seal gap[J]. Journal of China University of Mining & Technology,2008(3)634-636. [3] LI Decai, YUAN Zuyi. The theoretical analysis and experiment study of magnetic fluid seal [C]//The SICP.Beijing, 1995. 125-130. [4] 李德才. 磁性液体理论及应用[M]. 北京: 科学出版社, 2003. [5] ROSENSEIG R E. Fluid magnetic buoyancy [J].AIAA Journal, 1966, 4(10):1751-1758 . [6] LI Decai, YUAN Zuyi. The theoretical study of reciprocating axle magnetic fluid seal[J]. Journal of Mechanical Engineering, 1998(1):1-5. [7] BASHTOV OI V G. Modelling of magnetic fluid support [J]. Journal of Magnetism and Magnetic Materials, 2002(252):315-317. [8] BASHTOVOI V G, KABACHNIKOV D N, KOLOBOV A Y. Research of the dynamics of a magnetic fluid dynamic absorber[J]. Journal of Magnetism and Magnetic Materials, 2002(252): 312-314. [9] 潘公宇,杨海,徐腾跃,等.磁流变液阻尼器试验与建模研究[J].振动与冲击,2015,34(6):36-40. PAN Gongyu,YANG Hai,XU Tengyue,et al.Tests and modeling for magneto-rheological(MR) dampers[J].Journal of Vibration and Shock,2015,34(6):36-40. [10] 何新智.磁性液体加速度传感器的理论及实验研究[D].北京:北京交通大学,2011:56-65. Tests for magnetic fluid dampers ZHU Shanshan1,2, LI Decai1, CUI Hongchao1 (1.School of Mechanical, Electronic and Control Engineering Beijing Jiaotong University, Beijing 100044, China; 2.Beijing Vocational Technical College, Beijing 100042,China) Here,the effects of different inner surfaces and cone angles of a magnetic fluid damper on its vibration reduction performances were studied with tests based on the theory of second-order buoyancy. The test analysis results showed that the vibration reduction performance of a shell with rough inner surface is better than that of a shell with smooth inner surface; the vibration reduction performance of the damper with a larger cone angle is better than that with a smaller one in a certain range. magnetic fluid; shell; cone angle; vibration reduction performances 2015-05-08 修改稿收到日期:2015-10-11 TH212;TH213.3 A 10.13465/j.cnki.jvs.2016.19.031 作 者 朱姗姗 女,博士生,讲师
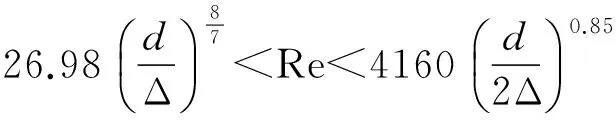






3 实验结果及分析



4 结 论
