钢连桥人致振动及TMD减振效应实测与分析*

2016-11-23王洪涛施卫星韩建平单伽锃

振动、测试与诊断 2016年3期

关键词：人行阻尼比测点

王洪涛，施卫星，韩建平，单伽锃

(1.同济大学结构工程与防灾研究所上海，200092)(2.兰州理工大学甘肃省土木工程防灾减灾重点实验室兰州，730050)

钢连桥人致振动及TMD减振效应实测与分析*

王洪涛1，施卫星1，韩建平2，单伽锃1

(1.同济大学结构工程与防灾研究所上海，200092)(2.兰州理工大学甘肃省土木工程防灾减灾重点实验室兰州，730050)

以某室外大跨轻柔钢结构人行桥为案例，介绍了该结构的设计概况及调谐质量阻尼器(tuned mass damper，简称TMD)减振设计，分别在结构施工完成后以及TMD装置安装后对其进行了实地动力测试，测得了该结构减振前后的模态特性以及在多种人行荷载工况下的振动响应，采用加速度峰值和均方根值为评价指标，分析了钢连桥人致振动情况及特性。结果表明：一端设计为滑动连接的钢连桥人致振动主要由第1阶竖向振型控制，扭动及水平振动响应相对较小；安装经优化设计的TMD装置后，整体连桥的频率特性没有明显变化，分布式TMD对多种频率激励工况均有良好的调谐减振作用，减振率达到35%～70%；共振激励下测得的原结构阻尼比较小，安装TMD后结构的阻尼比提高4倍，并且呈现出在自由振动衰减的前期较大，随着振动幅度变弱阻尼比降低；测试中发现TMD装置的减振效率对其阻尼比的变化不敏感。

人行桥；人致振动；调谐质量阻尼器；均方根响应；现场测试

引言

现代结构中一些跨度大、阻尼低的人行桥、楼板、廊桥以及楼梯等结构易在人活动荷载下发生较大振动，虽不至于使结构产生严重安全问题，但可能引起结构上使用者的不安全感和振动舒适性问题。现阶段对于上述结构的设计，最基本的原则是控制结构的基本振动频率，比如很多规范都控制其不小于3 Hz甚至5 Hz[1]。国内外现行的一些规范和技术指南也进一步采用加速度响应峰值、均方根值等指标进行振动舒适性的评价和控制[2-4]。在结构设计以及使用阶段，如果预测到结构的振动舒适度不满足，单纯加大设计截面以及加固原结构往往存在某些困难，比如建筑造型设计的要求、结构形式及造价等方面的限制，基于这一点，采用减振控制技术是一条可行且有效的途径。

TMD是一种实用、可靠的被动减振装置，常被应用于大跨轻质楼盖、人行桥以及高耸结构的减振中。TMD减振装置主要由调谐质量块、弹簧和阻尼装置三个部分组成。在对结构频率能准确调谐时，单TMD减振就能起到良好的减振效果，但为了提高调谐减振系统的鲁棒性，多质量调谐阻尼器(multiple tuned mass dampers，简称MTMD)得到越来越多的研究和应用[5-7]。中心TMD对结构主控频率调谐，考虑一定的频带宽度在主控频率上下一定范围内分布若干TMD，能有效改善单TMD 控制效果不稳定、适用激励频带过窄的缺点。以往的TMD减振控制研究中，主要是以数值模拟以及参数优化分析为主，对典型实际工程减振效果的现场测试分析较少，而这种分析能更加客观、真实地反映TMD减振装置的有效性，更具有工程指导价值。文献[8]对上海世博文化中心悬挑钢结构屋盖TMD减振控制做了研究，主要进行了有无TMD数值分析对比和实地测试的验证，得出了对同类工程有参考性的结论，但结构减振后的动力特性，比如阻尼特性以及不同人行荷载工况下的实际减振效率等还有待更具体的研究。

笔者以某大跨轻柔钢结构人行桥为案例，在主体结构施工完成后以及TMD系统安装后分别进行了现场动力测试，着重对比分析了连桥结构减振前后动力特性的变化、多种人行频率激励下的减振特性及效率。现场测试和分析的结果对人行桥人致振动及其控制措施的应用具有参考价值。

1 实测钢连桥的概况

笔者所测试分析的连桥为山西省某市文化综合展览馆中的一室外钢结构人行桥，桥体总长为62.9 m，桥面标高与室外地面平齐，横跨在该综合体结构负一层疏散楼梯的正上方，主要用于馆内外流动人员的疏散。其结构形式为单跨桁架，其上弦、下弦以及竖杆、斜杆均采用箱型截面钢构件，钢桁架高为2.2 m，宽为1.25 m。桥面板为20 mm厚钢板，上面浇筑一层100 mm钢筋混凝土板，桥面宽度为2.4 m。

由于钢连桥地处地震高烈度区，如与主体结构之间采用强连接，由于钢桥整体刚度较小，无法协调主体结构共同工作，在地震等作用下往往造成连桥结构的局部严重破坏。因此实际设计时连桥与主体结构之间采用了弱连接，在温度和地震等作用下，可以减小连桥和两端主体结构之间的相互影响，连桥的受力大大减轻。该人行桥的边界约束条件设计为一端刚接，一端采用抗震球形滑动支座。

该连桥结构设计采用轻质的型钢材，跨度大，又受到建筑设计的限制，造成其自振频率较低。设计阶段有限元分析该连桥第1阶竖向振动频率为1.95 Hz，振动模态振型为标准半正弦曲线，第1阶横向振动频率为1.76 Hz。结构主要频率在人体活动的主要频率范围内，服役期间可能引发人活动激励下的较大响应甚至引发共振响应，继而造成振动的舒适度问题。在满足安全的情况下，设计中采用质量调频阻尼器技术来改善结构的振动舒适度问题。

该连桥结构简图及测试测点布置如图1所示。

图1 钢连桥结构简图及测点布置Fig.1 The diagram of connecting bridge and measuring-point arrangement

2 环境振动测试及人行激励下响应测试

2.1 测试方法及测点布置

为了分析该钢连桥的动力特性以及在人行荷载下的振动响应，对其进行了环境激励下的振动测试和人行荷载下的振动测试。测试采用同济大学SVSA数据采集分析系统，灵敏度为50 V/g的Lance LC0132T和灵敏度为16.89 V/g的KD12000L的压电式加速度传感器。分别在连桥的桥面混凝土板结构层以及桁架下弦位置设置测试点，进行一定时间的连续观测，并记录振动时程数据。测点位置如图1所示。黑色方框为竖向测点，黑色三角框为水平向测点，原结构测试时布置TP1～TP6，TP13，TP14共8个测点，TMD安装后的测试布置TP4，TP7～TP15共10个测点，现场测试照片如图2所示。

环境振动测试期间为了尽量减小噪声的干扰，叫停周围一切施工、人体走动，采样频率均为100 Hz。

图2 钢连桥结构及现场测试照片Fig.2 Photos of the structure and in-situ test

2.2 环境振动测试动力特性识别

跨中竖向测点TP4以及横向测点TP14的振动加速度响应及其功率谱如图3所示。利用峰值拾取法和半功率点法，识别结构的振动频率和阻尼比。

图3 环境振动测试测点加速度时程及功率谱Fig.3 Accelerations and PSD of ambient vibration test

由图3(a)知，该连桥结构实际的竖向1阶振动模态频率为1.86 Hz，模态阻尼比为0.58%，其他竖向模态的振动相对于第1阶模态振动能量较低，可以判定该连桥竖向振动主要由1阶模态控制。由图3(b)知，横向1阶振动频率为1.66 Hz，其振动响应相对竖向振动小很多。

经典的结构动力学中用不同测点在固有频率处响应自功率谱的幅值比或者传递函数的幅值比可以获得结构的固有振型，另外也采用了更加精确的有理分式多项式方法来识别该结构的振型特性。由测点TP1～TP6的响应识别出的第1阶竖向模态振型呈现出近似半正弦形状，与结构原设计分析模态相同。

2.3 人行激励测试响应分析

由于该连桥结构主要设计功能为展览馆人行通道，服役期间可能承受多种情况的人活动荷载。对结构主体施工完成后进行人行激励下的动力测试，分析其人致振动特性，评估其振动响应。

分别进行单人在连桥跨中跳跃激励测试和人行走、跑动激励测试工况。

自由振动测试是一种常用的动力特性识别手段，特别是模态阻尼比的识别。由图3环境振动测试结果可知，1阶竖向模态占据主导地位。对于单一模态占主导的自由振动响应，模态阻尼比的估计可以通过用指数函数y=Ae-2πfξt拟合自由衰减响应的包络值而得出[9]。

2.3.1 单人跨中跳跃激励测试

选定单人(质量约为70 kg)在连桥跨中点以结构共振频率进行有节奏性的跳跃运动，跳跃的节奏由节拍器来精确控制。当激起结构较大振动时停止，同时测得人行桥自由振动测试加速度响应。

图4为在1.86 Hz激励频率下测点TP4所测得的振动响应时程及指数函数拟合识别阻尼比，其中为了验证拟合的精度，由希尔伯特变换方法做出了响应的包络值。

图4 自由振动测试加速度时程及阻尼比拟合Fig.4 Acceleration response of free vibration test and fitted exponential function

图4结果表明，自由振动测试使结构产生了较大的振动，加速度峰值接近40g。同时在现场测试中，激励个体及数据采集者在该桥上均感受到了较强的振颤，感官上产生了不舒适感。指数函数拟合法识别出的原结构模态阻尼比较小，仅为0.24%。

2.3.2 人行走及跑动激励测试

基于行人正常的步行、跑动频率范围，选定单人(质量约为70 kg)分别以1.74，1.86和1.95 Hz 3种频率进行有节奏性的步行，以2.06，2.24和2.5 Hz 3种频率进行有节奏性的跑动运动，其节奏均由节拍器精确控制。走动工况路径为从桥的一端走到另一端，再返回。因为桥面留有TMD装置安装孔，考虑到测试的安全性，跑动工况选定在跨中区域转圈跑动。选取测试中响应较大的跨中测点TP4为代表，图5中灰线为测得加速度响应时程。

图5 单人活动时连桥振动响应Fig.5 Response of bridge under single person excitation

国际上有关人行桥、楼板等结构人致振动方面的规范大都将加速度的峰值和均方根值(root mean square，简称RMS)作为评价指标。文献[10]指出，评估响应均方根指标时，选取不同时间步得到的均方根值存在差别。对于人行荷载响应，若选择1s或更大的时间步内产生单个脉冲的RMS响应估计，可能会忽略该段时间内其余激励步的脉冲。因此笔者对实际测得的加速度响应进行了连续(1/sf)s RMS响应计算，其中sf为人行走步频，取2 Hz。对各测试工况各测点加速度时程数据分别求整体均方根值和(1/sf)s时间步的连续均方根值。

由图5知，(1/sf)s连续RMS值比整体RMS值更能真实地反映瞬态振动响应，在一些时间段，前者明显高于后者，整体RMS值并不能表达振动整个时间段的响应变化情况，从而会低估结构的响应。

对比文献[4]中所建议的振动加速度峰值，在上述测试的共振激励工况中，虽然单人跳跃时结构竖向加速度峰值小于50 cm/s2，单人行走及跑动时小于15 cm/s2，但某些时间段的振动还是使桥上的人感受到了较强的振颤，感官上产生了不舒适感，因此有必要采取减振措施进行竖向振动控制。

测试中发现水平向振动相对较小，其加速度峰值、均方根值仅为竖向振动的1/5～1/8。测点TP13测得响应与测点TP4没有较大差异，说明该桥没有明显的扭转效应。

3 TMD减振后的减振效应实测与分析对比

3.1 TMD减振设计概述

TMD的参数优化主要是确定TMD装置最优的调谐质量以及阻尼比，选取 TMD 的最优刚度和阻尼系数的问题可转化为求解输入与输出的传递函数问题[11-12]，基于经典的Den Hartog公式确定了TMD减振的理论主控频率比和阻尼比分别为0.99和6%。考虑到本研究钢结构连桥的实际情况，为了提高减振效果的鲁棒性以及避免造成过大附加集中质量，考虑主控频率周围一定的频带宽度，分别在连桥中部区域的纵向下弦上安装3个TMD装置，其理论频率依次为1.67，1.84和2.03 Hz。TMD产品由上海路博橡胶减振器技术有限公司设计生产，单个TMD质量为1.2 t。TMD装置的安装示意以及现场照片如图6所示。

根据原结构施工完成后的现场测试结果，对TMD进行了出厂前调频，使各TMD的调频频率更适合实际结构。阻尼比的调整可以通过现场调整阻尼杆的高度，以使减振效果达到期望的程度。

TMD减振装置安装完成后，首先进行了环境振动测试。对比第2.2节，TMD安装前后，该连桥结构主要振动模态并没有明显变化，主频仍为竖向1.86 Hz，横向1.66 Hz，振动的频谱成分也相似。

3.2 减振前后人行激励测试对比分析

分别进行了单人在连桥跨中跳跃激励测试、行走及跑动激励测试。测试工况及处理方法同2.3节。

3.2.1 单人跨中跳跃激励测试对比

图7(a)为安装TMD后测点TP4在1.86 Hz激励频率下所测得的自由振动响应时程及指数函数拟合识别阻尼比。图7(b)为跨中测点TP7(中TMD上)在1.86 Hz激励频率下所测得的自由振动响应时程及指数函数拟合识别阻尼比。

图7 减振后自由振动测试时程及阻尼比拟合Fig.7 Acceleration response of free vibration test after TMD installed and fitted exponential function

比较图4和图7(a)，可以看出该钢结构连桥的阻尼比在安装TMD装置后有显著增大，在单人激起的最大加速度响应为5 cm/s2左右时，安装TMD后整体结构的阻尼比较原结构提高了4倍。减振后整体结构的阻尼比在自由振动衰减前5 s较大，随着衰减时间加长阻尼比降低，由0.96%降为0.56%。

由图7(b)可以看出，TMD装置的阻尼比也表现出与图7(a)中相同的特性，测试中最大的阻尼比能达到3%，随后阻尼比随振动强度减小而降低到1%以下，即TMD附加给主结构的阻尼变小，造成了主结构的阻尼特性发生了变化。

本研究所测试的各工况下，TMD装置的实测阻尼比没有达到设计中理论最优的阻尼比6%。这是因为现场TMD调试时，根据减振前后测试效果的比对，对TMD本身的阻尼比进行了调节；另外的原因可能是TMD的阻尼是速度相关型，在所测试的工况中并未达到一定的速度响应。但由以上实际对比分析看，在实际的阻尼比下整体结构的自由振动响应较原结构大大减小，衰减也明显加快，表明TMD的减振效果良好。文献[13]指出，在人活动激励下TMD的减振效率对自身阻尼比的变化不敏感，有时TMD阻尼比大并不一定会更大地减小整体结构的响应，而只是会减小TMD本身的振动。此外，各种TMD优化方法的阻尼比的预测差异也很大，但都能取得较好的减振效果。

3.2.2 人行走及跑动激励测试对比

分别以加速度峰值、整体均方根值以及(1/sf)s连续均方根值为指标，表1为各测试工况跨中测点TP4的TMD减振性能对比。可以看出单人步行时，1.86 Hz共振工况减振率最好，3种指标均能达到65%左右，另外两种激励工况TMD也有约50%的减振效率。单人跑动时，3种频率都不是共振频率，但也能得到较好的减振效果。2.06，2.5 Hz时均能达到50%以上的减振率，2.24 Hz激励工况TMD减振率较小，为35%左右。

图8为安装TMD前后测点TP4在共振工况下响应的(1/sf) s连续均方根响应对比，可以看出在共振激励下，TMD减振装置对整体结构的振动有较好的调谐减振作用。跳跃共振时，减振后结构响应均方根最大值较原结构降低了70%，而TMD质量块的振动响应均方根最大值约为主结构振动的6倍，说明TMD装置利用自身的振动对主结构的振动产生了良好的调谐作用，吸收部分振动能量，大大降低了主结构的振动响应。

对安装TMD后的结构进行了20人人群走动测试，人群中个体按照个人正常步态行走，如图9所示。图9(b)为测点TP4测得的加速度响应及均方根值，对照表1可以得出该工况振动中各评估指标均在可以接受的响应范围内。

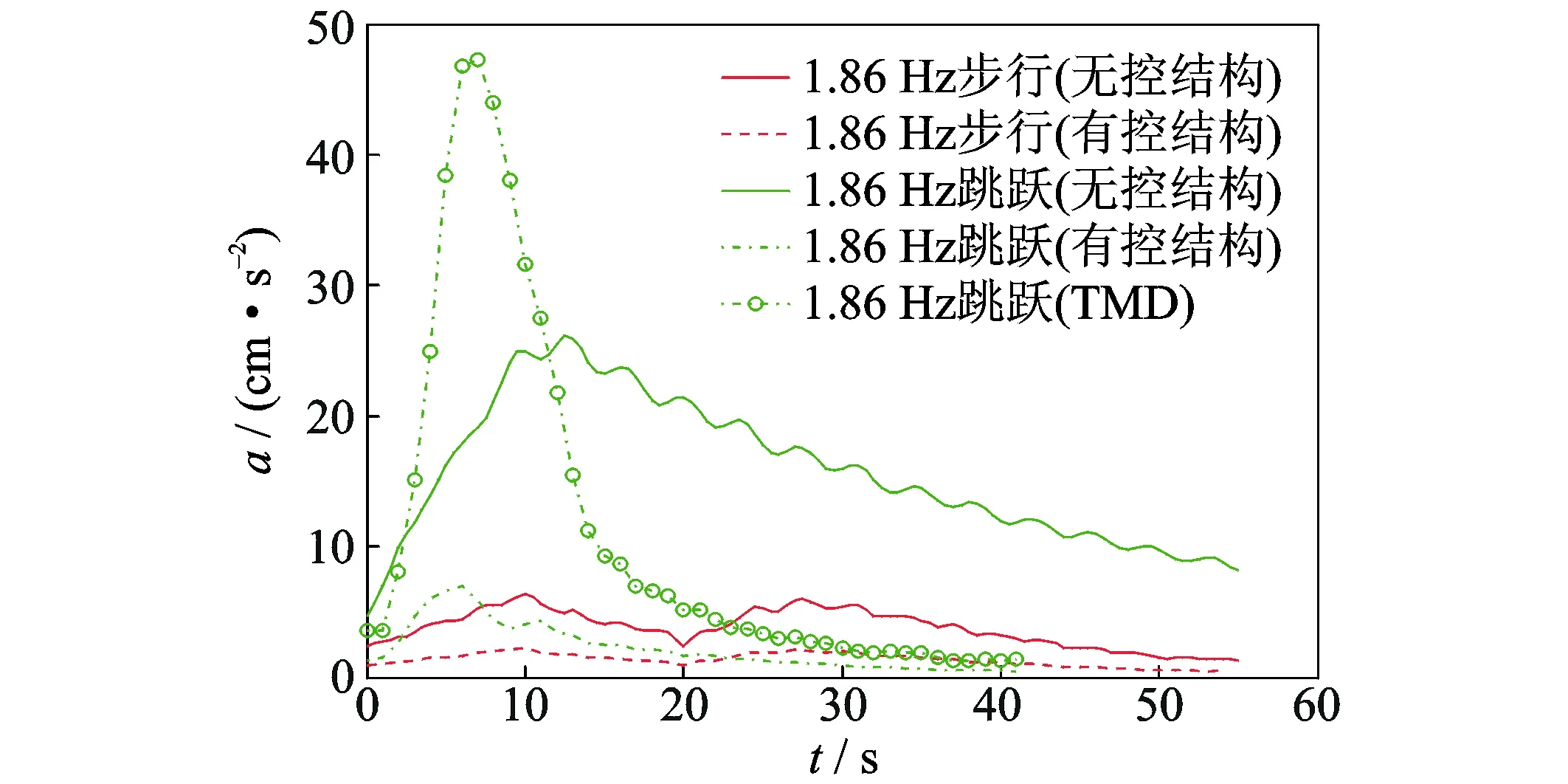
图8 减振前后共振激励测试的连续RMS值Fig.8 (1/sf)s RMS response with and without TMD under resonance excitation

4 结论

1) TMD装置安装后，连桥结构的振动频率没有明显变化，分布式TMD的设置形式对多种频率激励工况均有良好的调谐减振作用，减振率能达到35%～70%。

2) 安装TMD后整体结构的阻尼比较原结构提高4倍，并且呈现出在自由振动衰减的前期较大，随着振动幅度变弱阻尼比降低。

图9 20人群走动测试Fig.9 Test of footbridge under 20 persons walking

表1 TMD减振系统的竖向振动实测性能评估

Tab.1 Experimental performance assessment for vertical vibration of structure with TMD devices

cm/s2

3) 实际服役中TMD的阻尼比可能达不到理论最优的阻尼比，但也能得到良好的减振效果，在人活动激励下TMD的减振效率对自身阻尼比的变化不敏感。

4) 对TMD这种对调谐频率较敏感的减振装置，应在现场动力测试识别出结构的实际动力特性后再进行设计、调试，并且TMD的减振效率应得到实际测试对比的检验。

[1] Schlaich M. Guidelines for the design of footbridges: guide to good practice[M]. Switzerland: International Federation for Structural Concrete, 2005:55-60.

[2] Sétra F. Assessment of vibrational behaviour of footbridges under pedestrian loading[M]. France: Technical Guide Setra, 2006: 19-24.

[3] International Organization for Standardization. ISO 2631-2-2003 Mechanical vibration and shock-evaluation of human exposure to whole body vibration—part 2: continuous and shock-induced vibration in buildings (1 to 80 Hz)[S]. ISO 2631-2: 2003.

[4] GB13441.1-2007. 机械振动与冲击人体暴露于全身振动的评价——第一部分：一般要求[S]．北京: 中国标准出版社，2007.

[5] Zuo L, Nayfeh S A. Optimization of the individual stiffness and damping parameters in multiple-tuned-mass-damper systems[J]. Transactions of the ASME-L-Journal of Vibration and Acoustics, 2005, 127(1): 77-83.

[6] 樊健生，陈宇，聂建国．人行桥的 TMD 减振优化设计研究[J]．工程力学，2012，29(9) :133-140.

Fan Jiansheng, Chen Yu, Nie Jianguo. Optimum design of tuned mass damper for footbridge[J]. Engineering Mechanics, 2012, 29(9): 133-140. (in Chinese)[7] 马斐，张志强，李爱群. 大跨钢楼盖人群荷载激励下减振控制分析[J]．振动、测试及诊断，2013，33(3): 514-520.

Ma Fei, Zhang Zhiqiang, Li Aiqun. Vibration control analysis of large-span steel structure floor under crowd load[J]. Journal of Vibration, Measurement & Diagnosis, 2013，33(3): 514-520. (in Chinese)

[8] 吕西林，丁鲲，施卫星，等．上海世博文化中心TMD减轻人致振动分析与实测研究[J]．振动与冲击，2012，31(2): 32-37.

Lü Xilin，Ding Kun，Shi Weixing，et al．Analysis and field test of human-induced vibration reduction with TMD in Shanghai EXPO culture center[J]. Journal of Vibration and Shock，2012，31(2): 32-37. (in Chinese)

[9] Magalhães F, Cunha, Caetano E, et al. Damping estimation using free decays and ambient vibration tests[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1274-1290.

[10]Zivanovic S, Pavic A. Probabilistic modeling of walking excitation for building floors[J]. Journal of Performance of Constructed Facilities, 2009, 23(3): 132-143.

[11]李晓玮，何斌，施卫星. TMD减振系统在人行桥结构中的应用[J]．土木工程学报，2013，46(S1): 245-250.

Li Xiaowei, He Bin, Shi Weixing. Application of TMD seismic vibration control system in the bridge structures[J]. China Civil Engineering Journal, 2013，46(S1): 245-250. (in Chinese)

[12]同长虹，张小栋. 调谐质量阻尼器参数优化及其应用[J].振动、测试与诊断，2007，27(2): 146-149.

Tong Changhong, Zhang Xiaodong. Parameter optimization of toned mass dampers and its application to bridge vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2007, 27(2): 146-149. (in Chinese)

[13]Tubino F, Piccardo G. Tuned mass damper optimization for the mitigation of human-induced vibrations of pedestrian bridges[J]. Meccanica, 2015, 50(3): 809-824.