局部损伤的机械弹性车轮的静动态特性*

2016-11-23臧利国赵又群李小龙

振动、测试与诊断 2016年3期

关键词：固有频率车轮轮胎

臧利国，赵又群，李波，王健, 李小龙

(1.南京航空航天大学能源与动力学院南京，210016) (2.南京工程学院汽车与轨道交通学院南京，211167)

局部损伤的机械弹性车轮的静动态特性*

臧利国1，2，赵又群1，李波1，王健1, 李小龙1

(1.南京航空航天大学能源与动力学院南京，210016) (2.南京工程学院汽车与轨道交通学院南京，211167)

研究了輮轮的局部损伤对机械弹性车轮静动态特性的影响规律。根据车轮工作原理和结构特征，建立了非线性车轮有限元模型，利用模态分析的有限元方法计算了无损伤车轮的固有频率和振型；结合车轮的力学特性和充气轮胎的常见失效形式，对车轮的失效形式和危险区域进行了分析；采用刚度退化模型模拟车轮局部损伤，分析了不同位置、不同损伤状态下车轮固有频率的变化规律和静接地承载工况下的受力特征；将B级随机路面不平度作为动态激励输入，研究了局部损伤车轮的动态响应规律。研究表明：随着輮轮局部损伤程度的加深，车轮的固有频率逐渐降低，最大应力的位置不变，应力峰值变大；无损伤车轮的动态应力响应峰值小于局部损伤车轮的动态应力响应峰值；随着损伤程度的加深，在共振频段动态应力响应峰值变大，其他频段内变化不大。

车辆；机械弹性车轮；模态；局部损伤；静动态特性

引言

轮胎作为汽车行驶系统的重要组成，其功用主要有支撑整车质量、缓和路面冲击及产生驱动/制动力等，对汽车舒适性、平顺性等影响显著。采用充气轮胎的车辆存在刺破泄气和爆胎隐患，尤其是在高速行驶时，轮胎故障会引发重大交通事故。据统计，高速公路46%的交通事故是由轮胎发生故障引起的，仅爆胎一项就占轮胎事故总量的70%。车辆在160 km/h以上发生爆胎时，事故造成的死亡率接近100%[1]。因此，研发具有防爆胎、防刺破的高性能安全轮胎成为世界各大轮胎生产商的共识。

安全轮胎又称零压轮胎或跑气保用轮胎，常见形式主要有两种：非充气结构和充气结构。非充气结构安全轮胎主要有米其林的Tweel车轮[2]、仿生非充气车轮[3]、金属弹性车轮[4]和可变直径轮[5]等；充气结构安全轮胎在原有充气轮胎结构上进行改进，主要有自体支撑型和辅助支撑型两种[6]。但是，应用于机动车辆的安全轮胎仍存在自重过大、平顺性差及散热等问题[7]。

为解决以上问题，课题组提出一种基于某型越野车的机械弹性车轮，并在有限元建模、力学特性和通过性等方面进行了理论与试验研究[8-10]。与传统的充气轮胎不同，机械弹性车轮利用非充气结构的弹性材料替代轮胎的气体实现支撑、缓冲减振等功能。由于机械弹性车轮在与路面接触时承受随机交变载荷，加上复杂的行驶环境，不可避免地会出现损伤。笔者在前期研究的基础上，建立了考虑非线性因素的车轮有限元模型，通过车轮负荷特性试验验证模型的有效性，利用模态分析的有限元方法计算了无损伤状态车轮的固有频率和振型，并对机械弹性车轮的主要失效形式和危险区域进行了分析，采用刚度退化模型研究了輮轮局部损伤对机械弹性车轮静动态特性的影响规律。

1 机械弹性车轮结构与原理

机械弹性车轮突破传统车轮和轮胎的分体设计，采用铰链组连接弹性輮轮和轮毂的非充气结构，因此，不存在爆胎和刺破泄气的可能。车轮结构包括輮轮、铰链组及轮毂等部件，如图1所示。其中輮轮由弹性环、弹性环组合卡及橡胶层组成。

图1 机械弹性车轮结构示意图Fig.1 Mechanical elastic wheel simple mechanism

铰链组为弹性材料，由3节铰链构成，连接在輮轮和轮毂之间。其中，铰链1允许一定角度范围内的侧向运动，保证车轮具有良好的侧向稳定性和一定的侧向刚度。

机械弹性车轮的承载和变形如图2所示。当车轮静止承受垂直载荷时，輮轮受力变形，接地区域变平。除地面接触区域的铰链组外，其余均承受拉力。该承载方式既有顶部承载单位质量承载能力高的特点，又能从结构上保证车轮具有良好的附着性能。车轮滚动时，轮毂承受垂直载荷和力矩，并通过铰链组的拉伸将力传递到輮轮，使其产生设定范畴内的类椭圆弹性变形。

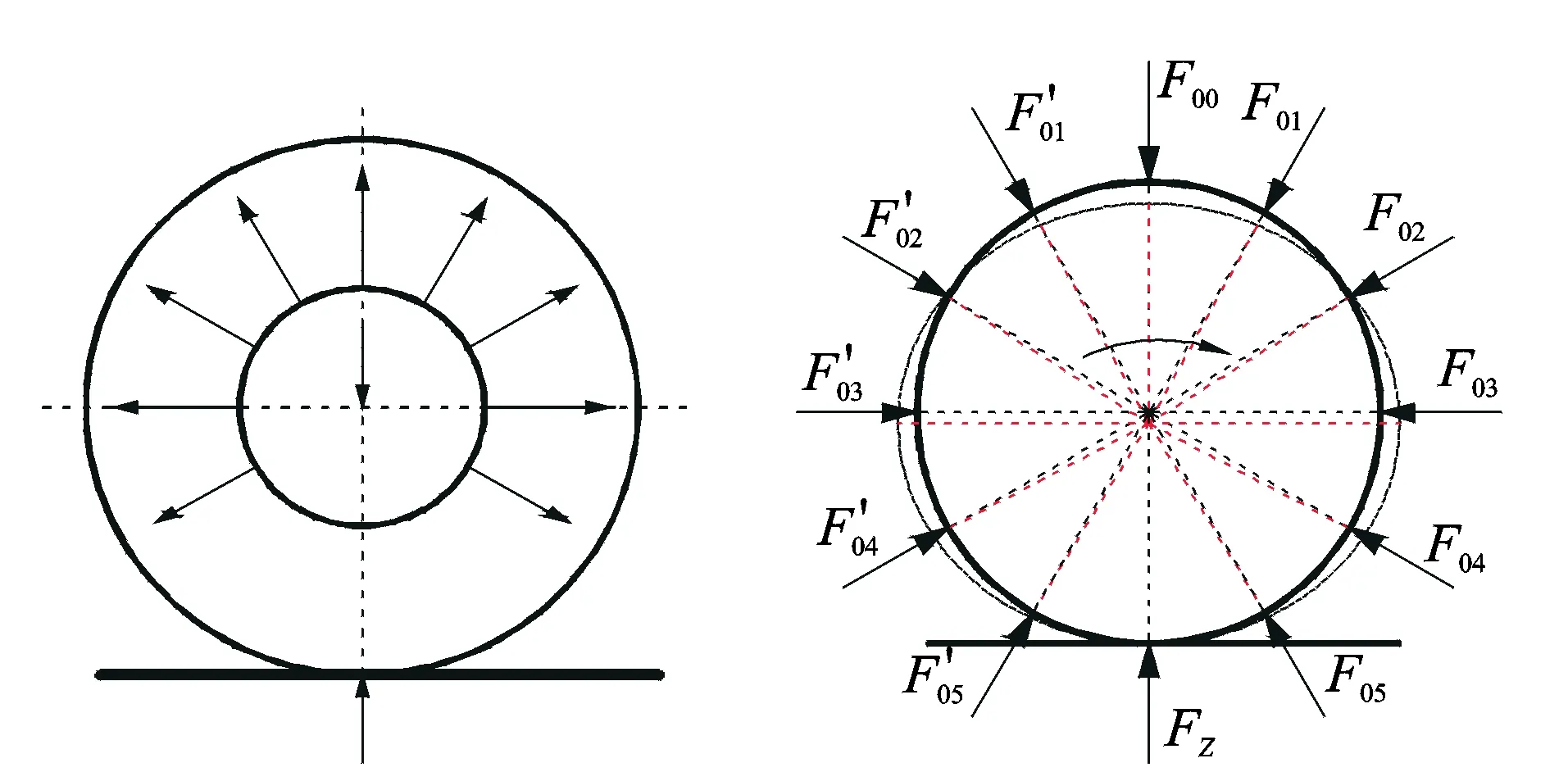
图2 机械弹性车轮的承载和变形Fig.2 Mechanical elastic wheel load way and deflection

2 机械弹性车轮模态分析

2.1 模态分析的有限元法

轮胎的模态参数是其本质特性，反映了轮胎的固有动力学特性。对不同结构轮胎的试验表明，模态参数与轮胎的结构特征和宏观特性有良好的对应关系，可应用于轮胎模型的建立和基本特性的研究[10]。模态分析的有限元法将结构模型离散化，建立单元特性矩阵，从而得到结构整体的运动微分方程

(1)

固有频率和主振型是结构振动系统的自然属性，是结构动态特性的重要部分。可以利用无阻尼自由振动求解，结构无阻尼自由振动微分方程为

(2)

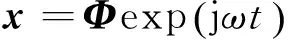
(3)

其中：Φ为结构的振幅列阵，即特征矢量；ω为系统的固有频率，即特征值。

式(3)为齐次线性方程组，有非零解的条件为系数行列式等于零，即

(4)

系统的主振型为

(5)

其中：Φ1，Φ2和Φn为各阶固有频率对应的主振型。

在建立车轮有限元模型时进行必要的简化处理，利用CATIA完成零部件的建模，再对车轮进行几何装配，通过沿中心轴的旋转而得到整个车轮的几何模型。利用HyperMesh划分有限元网格，赋予材料属性，设置接触方式，建立考虑接触非线性、材料非线性及几何非线性因素的有限元模型[7]，如图3所示。

图3 车轮有限元网格模型Fig.3 Mechanical elastic wheel mesh model

2.2 固有频率与负荷特性

利用模态分析技术对机械弹性车轮进行计算，得到车轮固有频率及振型。路面不平度对车轮的激励能量主要集中在低频段，因此实际行驶过程中，前几阶模态就能反映轮胎的动态特性[11]。利用模态分析的有限元法对机械弹性车轮的自由模态进行分析，得到机械弹性车轮的前8阶固有频率和振型，如表1所示。

在轮毂处施加不同的垂直载荷，并测得车轮的下沉量，可得到车轮负荷挠曲特性曲线，与样机负荷特性曲线进行对比，如图4所示。有限元分析结果与试验结果具有一致性，因此可以利用该有限元模型分析机械弹性车轮的力学性能。

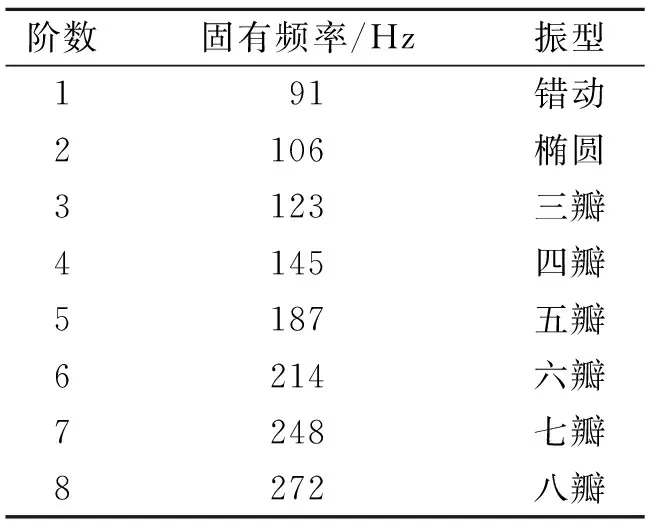
表1 固有频率与径向振型

图4 机械弹性车轮负荷挠曲特性曲线Fig.4 Mechanical elastic wheel load-deflection curve

静接地承载的工况下，在轮毂中心节点处施加6.8 kN的垂向载荷，机械弹性车轮的輮轮和弹性环的应力分布见图5。輮轮的最大应力位于最上方的中间位置，应力值σr=23.77 MPa，弹性环的最大应力位于最下部接地位置，应力值σl=17.09 MPa。

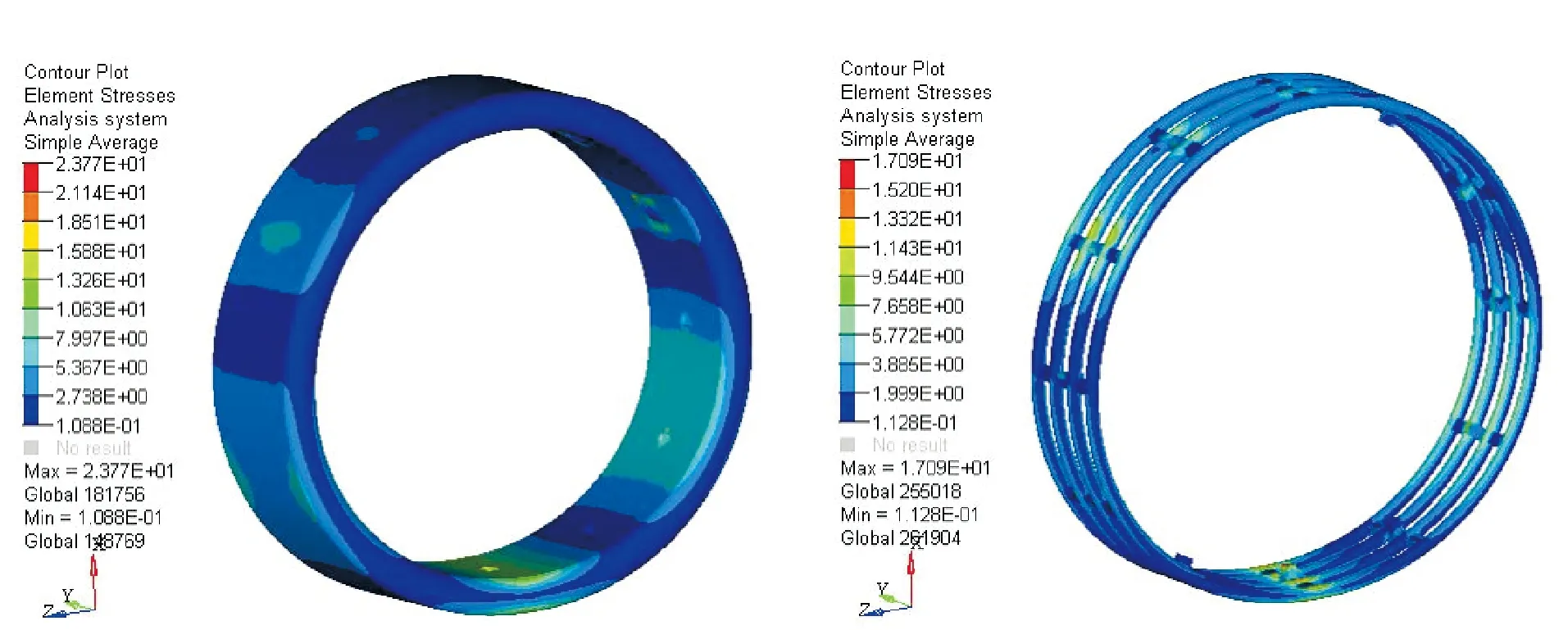
图5 静接地工况輮轮和弹性环的等效应力云图Fig.5 Von-Mises stress distribution of elastic wheel disk and elastic ring

3 失效形式与损伤模拟

3.1 失效形式分析

机械弹性车轮是传递力和力矩给车辆以响应驾驶员和车辆动态指令的部件，此外，还要承受多种道路路面、操作条件等复杂环境下的激励。在使用过程中，来自路面的随机激励和冲击会使车轮的主要承载部件产生疲劳损伤，车轮的承载、行驶速度还会影响橡胶胎面的强度。在模态分析的基础上，结合车轮实际工况和充气轮胎常见的失效形式，得出机械弹性车轮的基本失效形式有輮轮的疲劳损伤、冲击和道路危险损伤、胎面的磨损与脱落、铰链组的疲劳损伤、铰链组运动副的磨损等。其中輮轮是机械弹性车轮与地面直接接触、承受交变载荷的部件，也是决定车轮性能的关键部件，因此研究輮轮的损伤及对车轮性能的影响，对提高机械弹性车轮可靠性和安全性有重要的意义。

3.2 危险区域分析

依据机械弹性车轮力学特性和振型，分析机械弹性车轮輮轮的危险区域。利用刚度退化模型在危险区域设置刚度损伤模拟裂纹扩展，建立含輮轮局部损伤的有限元模型。

根据机械弹性车轮的结构力学特性和振型，輮轮的危险截面在振动剧烈和引起交变应力的振型节点附近。根据车轮的悬毂式承载特点，弹性环与铰链组的连接处承受随机交变载荷，且在车轮滚动过程中，与地面直接接触发生挠曲变形，因此这里是輮轮结构中的危险区域。图6所示为輮轮危险截面的4个节点。

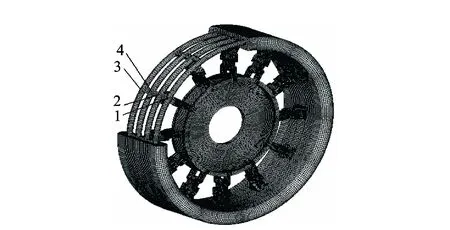
图6 輮轮内弹性环损伤位置Fig.6 Damaged location of elastic wheel

3.3 輮轮损伤模拟

材料刚度是一个宏观无损检测参数，能够描述材料在使用过程中的损伤状态[12]。在交变载荷作用下疲劳损伤不断累积，材料性质的劣化表现为材料刚度的下降[13]。

疲劳损伤耦合几何方程[14]为

(6)

其中：ui为位移分量的变程；εij为应变分量的变程。

引入损伤度D来表示材料劣化的程度，对于金属材料，损伤度可被看作标量，取值范围为[0,1]。

(7)

其中：E为材料无损伤时的弹性模量；ED为材料损伤度为D时的弹性模量。

考虑损伤度后，材料含损伤时的本构关系变为

(8)

其中：σij为应力分量的变程；Cijkl为弹性常数。

这一本构关系反映了损伤场与应力、应变场之间的耦合关系。

平衡方程为

(9)

其中：Bi为体力分量的变程。

引入等效应力变程

(10)

一般情况下，损伤演化方程[15]为

(11)

其中：N为应力循环次数；σMe为材料受到最大载荷时对应的等效应力；σme为材料受到最小载荷时对应的等效应力；E为材料的弹性模量；α，p为材料的损伤力学参数；σth应力门槛值，可由材料的疲劳性能曲线确定。

应力门槛值可表示为

(12)

其中：σth0为无初始损伤时对应的应力门槛值；ν为材料损伤参数。

将式(12)代入损伤演化方程，可得

(13)

通过修改损伤部位的单元刚度来模拟裂纹类损伤，利用损伤力学-有限元法可计算新的损伤场条件下的固有频率。

4 局部损伤对车轮静动态特性的影响

4.1 固有频率与静态特性

分别计算弹性环上4处不同节点的单元刚度下降10%，20%和30%的机械弹性车轮的固有频率，其中节点1在不同损伤下的车轮固有频率如表2所示。

表2 不同损伤下的固有频率

由表2可以看出,随着局部损伤的加深，车轮固有频率呈下降趋势。在其他3处节点的损伤对车轮固有频率的影响与上述结果基本一致。

当弹性环有不同程度的损伤时，分别计算了车轮在静接地承载工况下车轮的应力分布情况。研究表明,輮轮和弹性环产生最大应力的位置不变，且最大应力值数值变化不大。但是在损伤节点位置处，随着损伤的加剧，应力值逐渐变大，出现应力集中现象。由于车轮结构的对称性，其他3处节点的损伤对车轮结构力学特性的影响与上述结果基本一致。

4.2 动态响应特性

分别对无损伤和局部损伤的机械弹性车轮在路面激励下的响应进行分析，研究局部损伤对车轮动态特性的影响规律。根据随机过程采样定理和路面不平度分级，编写Matlab程序生成B级随机路面不平度,如图7所示。

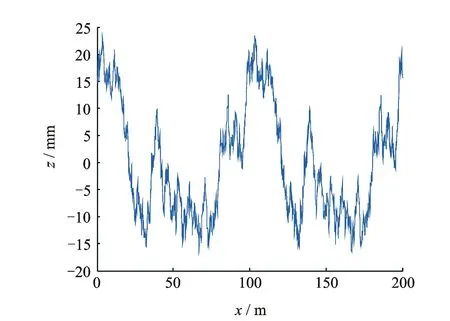
图7 B级随机路面不平度Fig.7 Random road roughness of level B

将此路面不平度作为动态特性分析的输入激励，得到损伤节点的动态应力响应。计算了在同一损伤状态下，不同位置节点1和节点2单元刚度分别下降20%的动态应力响应，如图8和图9所示。

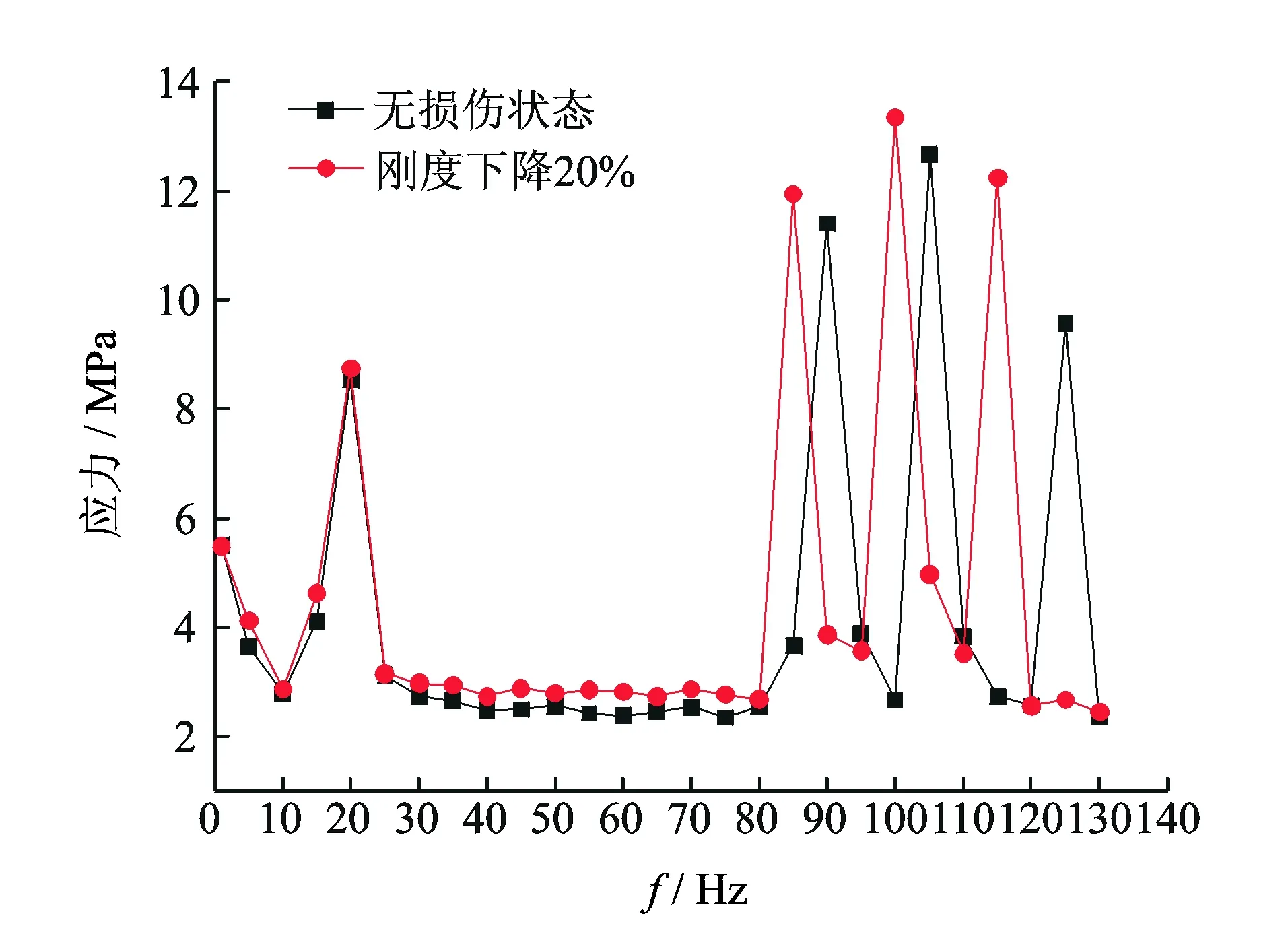
图8 损伤状态下节点1的动态应力响应Fig.8 Dynamic stress responses of element 1 in damaged condition

图9 损伤状态下节点2的动态应力响应Fig.9 Dynamic stress responses of element 2 in damaged condition

由图可知，机械弹性车轮在10～30 Hz和80～130 Hz频带内有较明显的动态应力响应，这是由于路面不平度激励与车轮产生共振引起的。无损伤状态下车轮的动态应力响应峰值小于局部损伤状态下的动态应力响应峰值，且局部损伤车轮的共振频率点发生偏移，共振频率点的偏移规律与损伤状态下固有频率的计算结果一致。由于车轮结构的对称性，其他危险区域节点3和节点4损伤状态下的动态应力响应规律与节点1和节点2的基本一致。

此外，还计算了同一节点位置在不同损伤状态下的动态应力响应规律，如图10所示。由图可知，随着损伤程度的加深，在共振频率处动态应力响应峰值变大，其他频段内的动态应力响应变化不大。

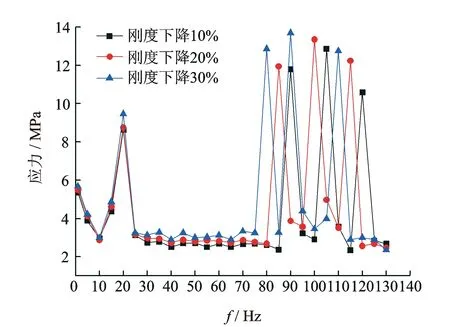
图10 节点1在不同损伤下的动态应力响应Fig.10 Dynamic stress responses of element 1 in different damaged conditions

由于机械弹性车轮的结构特征，弹性环位于輮轮内部，含局部损伤的车轮的试验研究比较困难，且费用昂贵。利用模态分析的有限元方法，采用刚度退化模型模拟计算局部损伤状态下车轮的固有频率和静态特性。根据随机过程采样定理，生成B级随机路面激励，通过响应分析方法获得无损伤状态和不同损伤状态的动态响应规律，为车轮健康状态监测和故障诊断提供了参考。

5 结论

1) 面机械弹性车轮的輮轮是与地面直接接触、承受交变载荷的部件，輮轮的疲劳失效是机械弹性车轮的主要失效形式之一。

2) 随着损伤程度的加深，机械弹性车轮的固有频率逐渐降低，在静接地承载工况，輮轮产生最大应力的位置不变，应力峰值变大，更容易出现应力集中现象。

3) 无损伤状态的车轮动态应力响应峰值小于含局部损伤车轮的动态应力响应峰值，且含局部损伤车轮的共振频率点发生偏移。随着损伤程度的加深，在共振频率处动态应力响应峰值变大，其他频段内的动态应力响应变化不大。

[1] Jang I G, Sung Y H, Yoo E J, et al. Pattern design of a non-pneumatic tyre for stiffness using topology optimization [J]. Engineering Optimization, 2011, 42(2): 119-131.

[2] Bras B, Cobert A. Life-cycle environmental impact of michelin Tweel tire for passenger vehicles[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2011, 4(1):32-43.

[3] Kim K, Kim D M. Contact pressure of non-pneumatic tires with hexagonal lattice spokes[C]∥SAE Congress and Exhibition. Warrendale:SAE International,2011.

[4] 李莉，胡立臣，邵朋礼. 一种新型轮胎的设计与分析[J].工程设计学报，2008，15(3)：220-224.

Li Li, Hu Lichen, Shao Pengli. Design and analysis of a new tire[J]. Journal of Engineering Design, 2008,15(3):220-224.(in Chinese)

[5] Chen Xinbo, Gao Feng, Wang Zhe, et al. Mechanism principle and dynamics simulation on variable diameter walking wheel[C]∥ 2011 Second International Conference on Digital Manufacturing & Automation. Piscataway:IEEE Computer Society,2011:723-727.

[6] 佟金，杨欣，张伏，等. 零压续跑轮胎技术现状与发展[J]. 农业机械学报，2007,38(3):182-187.

Tong Jin, Yang Xin, Zhang Fu, et al. Development of run-flat tire technology[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(3):182-187. (in Chinese)

[7] Rhyne T B, Cron S M. Development of a non-pneumatic wheel[J].Tire Science and Technology, 2006, 34(3): 150-169.

[8] 岳红旭，赵又群. 一种新型安全车轮的非线性有限元分析[J]. 中国机械工程，2012，23(11)：1380-1385.

Yue Hongxu, Zhao Youqun. Nonlinear finite element analysis of a new safety wheel[J]. China Mechanical Engineering, 2012, 23(11):1380-1385. (in Chinese)

[9] Wang Wei, Zhao Youqun, Wang Jian, et al. Structure analysis and ride comfort of vehicle on new mechanical elastic tire[C]∥Proceedings of the FISITA 2012 World Automotive Congress. Beijing: Springer Berlin Heidelberg,2013:199-209.

[10]汪伟，赵又群，姜成，等. 新型机械弹性车轮的建模与通过性研究[J]. 中国机械工程，2013，24(6)：724-729.

Wang Wei, Zhao Youqun, Jiang Cheng, et al. Ride comfort of vehicle on new mechanical elastic wheel[J]．China Mechanical Engineering，2013，24(6)：724-729．(in Chinese)

[11]Fan Chengjian, Guan Dihua. The quantitative analysis and experimental verification of the tire static enveloping model using experimental modal parameters[J].Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility,2006,44(9):675-688.

[12]张晓阳，孙蓓蓓，陈南，等. 基于修正Craig-Bampton方法的轮胎动态子结构模型[J].农业机械学报，2009，40(9)：41-45.

Zhang Xiaoyang, Sun Beibei, Chen Nan, et al. Dynamic substructure tire model based on modified Craig-Bampton method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2009, 40(9): 41-45. (in Chinese)

[13]张旭，邢静忠. 叶片局部损伤对大型水平轴风力机静动态特性影响的仿真分析[J].工程力学，2013，30(2)：406-412.

Zhang Xu, Xing Jingzhong. Simulation analysis on the effect of local damage of blade on static and dynamic characteristics for large horizontal axis wind turbine[J].Engineering Mechaanics,2013, 30(2): 406-412. (in Chinese)

[14]张君男，殷之平，黄其青，等. 基于损伤力学方法的铆接结构疲劳寿命预估[J].应用力学学报，2013，30(5)：747-752.

Zhang Junnan, Yin Zhiping, Huang Qiqing, et al. Fatigue life prediction of the aircraft riveted structure based on damage mechanics[J]. Chinese Journal of Applied Mechanics, 2013, 30(5): 747-752. (in Chinese)

[15]杨继运，张行，张珉. 基于疲劳裂纹形成曲线的裂纹扩展分析数值方法[J].机械工程学报，2004， 40(7)：55-62.

Yang Jiyun, Zhang Xing, Zhang Min. Numerical method for crack extension analysis based on fatigue crack formation curve [J]. Journal of Mechanical Engineering, 2004, 40(7): 55-62. (in Chinese)