超大口径天线结构的风振响应*

2016-11-23钱宏亮

振动、测试与诊断 2016年3期

关键词：风振反射面风洞试验

刘岩，钱宏亮，范峰

(1.长安大学建筑工程学院西安，710061) (2.哈尔滨工业大学土木工程学院哈尔滨，410075)

超大口径天线结构的风振响应*

刘岩1，钱宏亮2，范峰2

(1.长安大学建筑工程学院西安，710061) (2.哈尔滨工业大学土木工程学院哈尔滨，410075)

为明确大型天线结构风振响应特性，以待建的110 m全可动天线为研究平台，对其展开各迎风姿态下的风荷载特性分析。根据刚性模型风洞试验结果，探讨了反射面平均风压分布规律及最不利风向角。在此基础上，采用基于随机振动理论的非线性时程分析法进一步对结构的风致动力响应展开研究，总结了风振响应特性。结果表明，该结构自振频率分布密集，结构较柔，其风振响应是一个窄带过程，振动能量随着俯仰角的增大而逐渐提高，且高阶振型逐渐对风致振动有所贡献。该成果可为天线结构抗风设计提供较为全面的荷载取值参考。

天线结构；刚性模型；风振响应；自振频率；抗风设计

引言

风荷载作用会造成天线结构反射面几何形状的变化，严重影响其分辨率和灵敏度，致使工作性能降低[1-3]。因此，对反射面风荷载特性的分析显得尤为重要。早期对于天线结构风压及风荷载的研究，主要采用的是理论计算或风洞试验。刘彦等[4]研究了反射面变形对天线辐射性能的影响，结果表明在对水平面方向图的影响因素中，反射面变形占据了主导地位，而这一因素对垂直面方向图影响较小。由此，风荷载对于天线性能的影响引起普遍关注，尤其是风致天线结构变形得到了进一步研究。Lombardi等[5]通过风洞试验研究了天线结构的风荷载，获得了反射面风压系数，同时研究了反射面镂空度、方位枢轴位置等因素对天线风荷载的影响，并与静态下的模型试验结果进行了比较，结果表明两种模型所受风荷载差别较大。Gawronski等[6]对深空站天线结构DSS-13进行了风洞试验研究，获得了风力矩系数，并与现场实测数据进行了比照，结果表明现场实测数据与风洞试验数据误差小于10%，并在试验的基础上，对作用在天线上的风荷载进行了计算，进一步分析了天线结构的风致指向误差。

近些年，计算流体动力学(computational fluid dynamics,简称CFD)数值模拟技术在结构风工程研究领域得到了广泛应用，并已成为研究结构风荷载的主要手段之一，这一技术开始逐步应用于射电天文领域。Mahmoud等[7]对大型天线结构的球形保护罩分别进行风洞试验和CFD数值模拟，对两种不同研究途径下的数据进行比较，发现二者吻合较好。Polsky等[8]采用CFD求解器COBALT对船舰上天线桅杆的流场尾流进行过大涡数值模拟计算。杜强等[9]对雷达天线的平均风荷载特性进行了数值模拟研究，并提出了采用工业风洞试验研究天线平均风荷载特性时的洞壁干扰修正方法。

综上所述，国内外对于天线结构风场的研究主要集中在对光学天线及其球形保护罩内、外流场的数值模拟方面，而采用风洞试验进行研究的天线结构形式又较为特殊，种类偏少，存在一定局限性，且相关研究成果对于全可动天线结构风荷载特性的全面把握显得十分匮乏。因此，对巨型全可动天线反射面结构的风压分布规律、整体风力系数及风振响应特性的研究亟待展开。

笔者以待建的新疆110 m天线为研究平台，根据其典型工况下的风洞试验结果，分析了反射面平均风压分布及结构自振特性。在此基础上，采用非线性时程分析方法对结构的风致动力响应展开研究，总结其风振响应特性及分布规律，并为结构任意迎风姿态下的抗风设计提供了荷载取值参考。

1 计算模型及动力特性

1.1 有限元模型

全可动天线结构主要由副反射面、主反射体、俯仰机构、方位座架及轮轨系统等组成，如图1所示。

图1 全可动天线结构模型Fig.1 All movable telescope structure model

副反射面采用铝蜂窝夹层结构，在45°方向由4榀钢桁架作为支撑系统将其支撑在主反射面表面；主反射体由铝蜂窝面板和调整促动器构成，连接于背架结构上弦，背架结构通常采用空间桁架体系，其主要作用是承接主反射面并维持其几何面型；俯仰机构由扇形大齿轮、俯仰轴承座及俯仰平台构成，俯仰轴承座安装于方位座架的两个顶点，整个俯仰机构通过扇形大齿轮的驱动便可绕这两点轴承座从5° 转至90°，如图2所示；方位座架为箱型截面构成的空间框架结构，支承于底部的方位滚轮之上[10-11]。针对天线结构各部分受力特点，研究分析中采用不同的计算单元予以模拟。表1为模型中单元使用情况说明，而平台、护栏、馈源和机房等附属部分均以集中质量的形式施加于结构相应节点[12]。

图2 俯仰角转动范围Fig.2 Pitch angle coverage

组成部分模拟单元背架结构Pipe16核心筒、扇形大齿轮Shell63俯仰机构、方位座架、促动器Beam4驱动杆Link8配重Mass21反射面板Shell181

1.2 自振特性分析

自振频率是分析结构动力响应的重要参数，结合风洞试验典型工况，选取天线结构变位中的4种典型俯仰姿态，采用子空间迭代法对结构自振特性进行分析。这里以90°俯仰角模型为例，表2给出模型前10阶自振频率值，可见该结构自振频率分布密集，各相邻振型间频率十分接近，且基频较低，结构较柔。限于篇幅，只给出模型前2阶振型及振型描述，如图3所示。其余振型多表现为结构的局部振动或者扭转。

表2 结构前10阶自振频率

Tab.2 Ten order Frequencies of the telescope structure

阶次f/Hz阶次f/Hz10.88761.54521.03271.68131.15881.84341.21491.97251.358102.125

图3 结构振型Fig.3 Mode of vibration

2 风洞试验

2.1 试验模型及测量系统

风洞试验在哈尔滨工业大学边界层风洞与浪槽联合试验室中进行，该试验段尺寸宽为4 m，高为3 m，长为25 m。试验风速在3～50 m/s范围内连续可调。流场校测和实际使用结果均表明，该风洞流场的速度均匀性、平均气流偏角和湍流度等流场质量良好，能量比较高，噪声与振动较低，均满足相关设计要求[13]。测压系统采用美国Scanivalve电子式压力扫描阀系统。

试验模型如图4所示，采用缩尺比为1/200的刚性模型，模拟大气边界层风场的地貌类型为B类，地面粗糙度指数为0.16。

图4 风洞试验模型Fig.4 Experimental model in the wind tunnel

反射面镜面采用亚克力有机玻璃制作，厚为5 mm，管线布置夹层厚度最小值取10 mm，如图5所示。反射面凹面和凸面各布置91个测压点，其布置如图6所示。风向角定义如图7所示，试验中，在0°～180°范围内，每隔30°转动1次作为试验风向角，俯仰角在5°～90°内选取5°，30°，60°及90°为试验定位俯仰角。测量分析工况共计22个(90°俯仰角下，关于中心轴任意风向角呈极对称，因此只需选1种风向角即可)。

图5 反射面剖面图(单位:mm)Fig.5 Reflector section plan of the test mode (unit: mm)

图6 测点布置Fig.6 Pressure tap arrangement

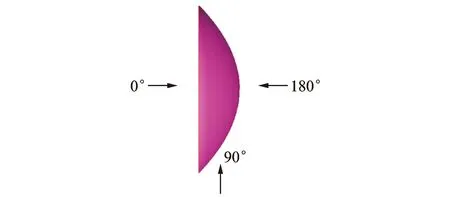
图7 风向角示意Fig.7 Wind direction angle

2.2 平均风压测试

根据相似理论，试验数据处理为

(1)

其中：n为频率；L为尺寸；U为风速；m为缩尺后的模型；p为真实结构。

由此可得相关变量相似比如表3所示。

表3 变量相似比

Tab.3 Scaling laws for variables

名称模型值原型值相似比直径/mm5501100001∶200速度/(m·s-1)14561∶4时间/s209961∶50

模型上各测压点的风压值采用无量纲压力系数表示

(2)

其中：Cpi(t)为第i测压孔的风压系数；Pi(t)为结构表面测点压力值；P0和P∞分别为参考点处平均总压和平均静压。

通过分析比较各俯仰角姿态下不同风向角的平均风压分布规律，发现风向角对反射面的风压分布有较大影响。从现有风洞试验数据中看，当风向角在0°左右时，上述风洞试验中反射面表面皆表现为正压。随着风向角增大至90°时，结构表面风压力逐渐减小，并从反射面边缘开始出现风吸力。对于0°俯仰姿态下的180°风向角工况，反射面总体上皆处于负压作用，主要由于反射面凸面受到正压，而凹面在分离流和尾流作用下受到风吸力作用引起。针对天线同一俯仰角姿态，在不同风向角下，由于壁面气流的分离点位置和尾流作用有所差异，因此反射面平均风压(风压力或吸力)最大值出现位置也不同。此外，对于大多数俯仰角及不同风向角工况，来流通常在反射面边缘处产生明显的气流分离，故反射面最大负压值一般出现在迎风边缘区域。

图8 5°俯仰角不同风向角反射面平均风压分布Fig.8 Mean wind pressure coefficients of the reflector in different wind directions for 5°pitch angle

图9 30°俯仰角不同风向角反射面平均风压分布Fig.9 Mean wind pressure coefficients of the reflector in different wind directions for 30°pitch angle

图10 60°俯仰角不同风向角反射面平均风压分布Fig.10 Mean wind pressure coefficients of the reflector in different wind directions for 60°pitch angle

图11 90°俯仰角不同风向角反射面平均风压分布Fig.11 Mean wind pressure coefficients of the reflector in different wind directions for 90°pitch angle

3 风振响应计算

3.1 风振响应分析方法

采用非线性时程分析法对天线结构进行风振响应分析，这里求解结构动力响应时采用Newmark-β法直接进行时程计算，具体步骤如图12所示。笔者对结构风振响应分析中采用风压时程序列取自风洞试验。通过试验中刚性模型表面测点布置，采用空间插值加密法，根据大气边界层风场中真实结构测点处的来流风速确定作用在结构上的脉动风压时程[14-15]。

图12 Newmark-β法计算流程Fig.12 Calculating flow chart for the method of Newmark-β

3.2 风振系数的确定方法

3.2.1 位移风振系数和内力风振系数

进行结构动力响应分析目的是为了获得脉动风荷载对结构的影响，并将之转化为工程设计人员直接使用的设计荷载。根据《建筑结构荷载规范》，通常采用风振系数来考虑风荷载的动力效应，其表达式为

(3)

由于天线结构反射面部分属于典型的大跨空间结构，风荷载复杂，准定常假定一般不适用，这使得结构脉动风的动力作用难以估算。这种天线结构自振周期较大，结构偏柔，对脉动风荷载十分敏感。为此，笔者采用直接基于结构响应的风振系数，即采用位移风振系数和内力风振系数，其表达式为

(4)

具体计算如下

(5)

其中：sign代表符号函数；σy为脉动风响应均方差；g为峰值因子。

按式(6)计算

(6)

其中：T为观测持时(通常为1 h)；v为水平跨越数，通常取值在3.0～4.0，这里取3.5。

3.2.2 整体风振系数

采用式(4)即可得到结构各点的位移风振系数和各根杆件的内力风振系数。大跨度结构的自振频率分布密集，各相邻振型间频率十分接近，且基频较低，主要贡献模态往往出现在高阶振型，因此风振控制点准确位置难以判断。笔者进一步采用最大动力响应为控制指标的整体位移风振系数和整体内力风振系数的概念，具体方法为

(7)

(8)

另外，考虑到脉动风实际上是一个随机过程，响应均方差只是一个具有一定保证率的动力响应幅值(均为正值)，因此在与静风效应叠加时，应考虑正向和负向叠加，即应考虑Uwi±gσUwi和Swi±gσSwi两种组合。

3.3 分析方案及响应指标

根据风洞试验分析结果，天线结构在3种俯仰姿态下的整体阻力系数如图13所示。阻力系数均在0°风向角时最大(此时为凹面迎风，受力投影面最大)，因此风振响应分析时统一选取0°风向角，具体俯仰角分别为5°，30°和60°。结合大跨空间结构的特点和设计人员所关心的风振响应，以反射面节点法向位移和杆件轴向应力+弯曲应力作为风振响应指标。

图13 阻力系数随风向角变化曲线Fig.13 Cd in different directions

3.4 结构风振响应结果分析

3个模型极值应力时程及极值位移时程如图14(a)～图19(a)所示。为了在频域内分析结构在脉动风荷载作用下的响应特性，采用傅里叶变换，将响应时程进行时域到频域的转换，得相应的极值应力与位移功率谱密度函数如图14(b)～图19(b)所示。根据功率谱密度函数可以看出，天线结构的风振响应是一个窄带过程。对于同一俯仰角模型而言，极值应力功率谱与位移功率谱在对结构的动力响应特征上呈现高度一致。结合前述结构自振频率，对于5°俯仰角，均表现出振动的能量主要集中在结构第1阶频率(0.7 Hz)附近；对于30°俯仰角，依然表现出振动的能量主要集中在结构第1阶频率(0.7 Hz)附近，不过能量幅值有所增大；对于60°俯仰角，结构表现出振动的能量开始往高阶频率发展，从能量分布图可以看出，在0.9和1.1 Hz附近均出现了峰值(分别对应3阶、4阶频率)，即高阶振型明显参与进来，开始对风致振动有所贡献。能量幅值和俯仰角间的变化关系表现出振动能量随着俯仰角的增大而逐渐增高。后续给出各模型的极值应力分布及极值位移分布，分别如图20～图22所示，图中极值应力和极值位移分布是根据式(6)计算获得的在整个时程当中各杆件单元最大应力值和各节点最大位移值(主要表现为z向振动)。从极值应力分布图看出，在0°风向角下，3个模型中最大的应力主要集中在上弦第2环的径向杆，最大值可达170 MPa，出现在30°俯仰角姿态；从极值法向位移图看出，在0°风向角下，位移表现为沿竖向轴左右对称，且各模型的位移极值主要集中在反射面的上、下悬挑端和两侧悬挑端，3个模型中法向位移最大为24 cm，出现在5°俯仰角姿态。限于篇幅，其他俯仰角的计算结果可参见表4。根据时程分析结果确定了天线结构在各俯仰角下的极值响应后，同时未来结构抗风设计分析提供了风振系数取值依据，如表4所示。

图14 5°俯仰角模型极值应力Fig.14 The extreme stress for the 5°pitch angle model

图15 30°俯仰角模型极值应力Fig.15 The extreme stress for the 30°pitch angle model

图16 60°俯仰角模型极值应力Fig.16 The extreme stress for the 60°pitch angle model

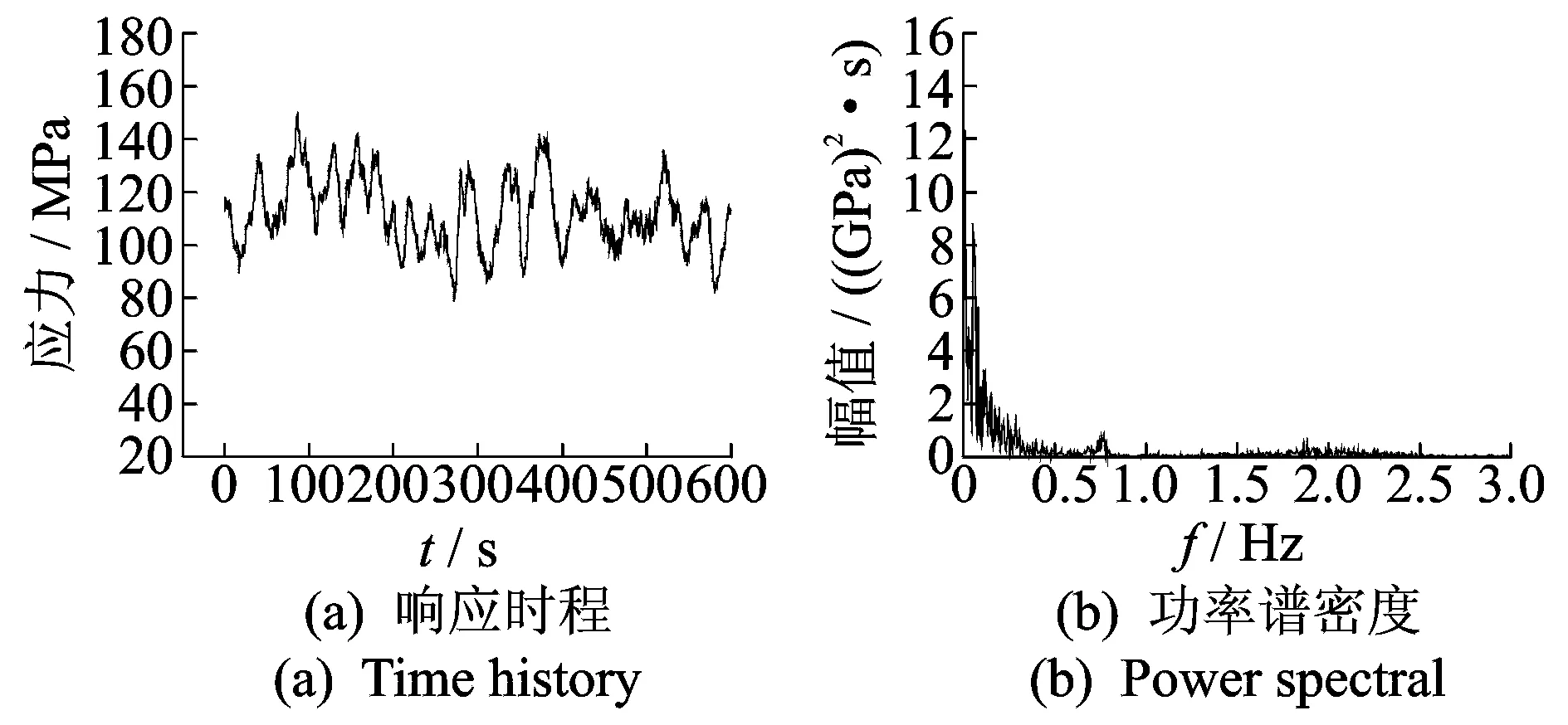
图17 5°俯仰角模型极值位移Fig.17 The extreme displacement for the 5°pitch angle model

4 结论

1) 天线结构自振频率分布密集，各相邻振型间频率十分接近，且基频较低，结构较柔。

图18 30°俯仰角模型极值位移Fig.18 The extreme displacement for the 30°pitch angle model

图19 60°俯仰角模型极值位移Fig.19 The extreme displacement for the 60°pitch angle model

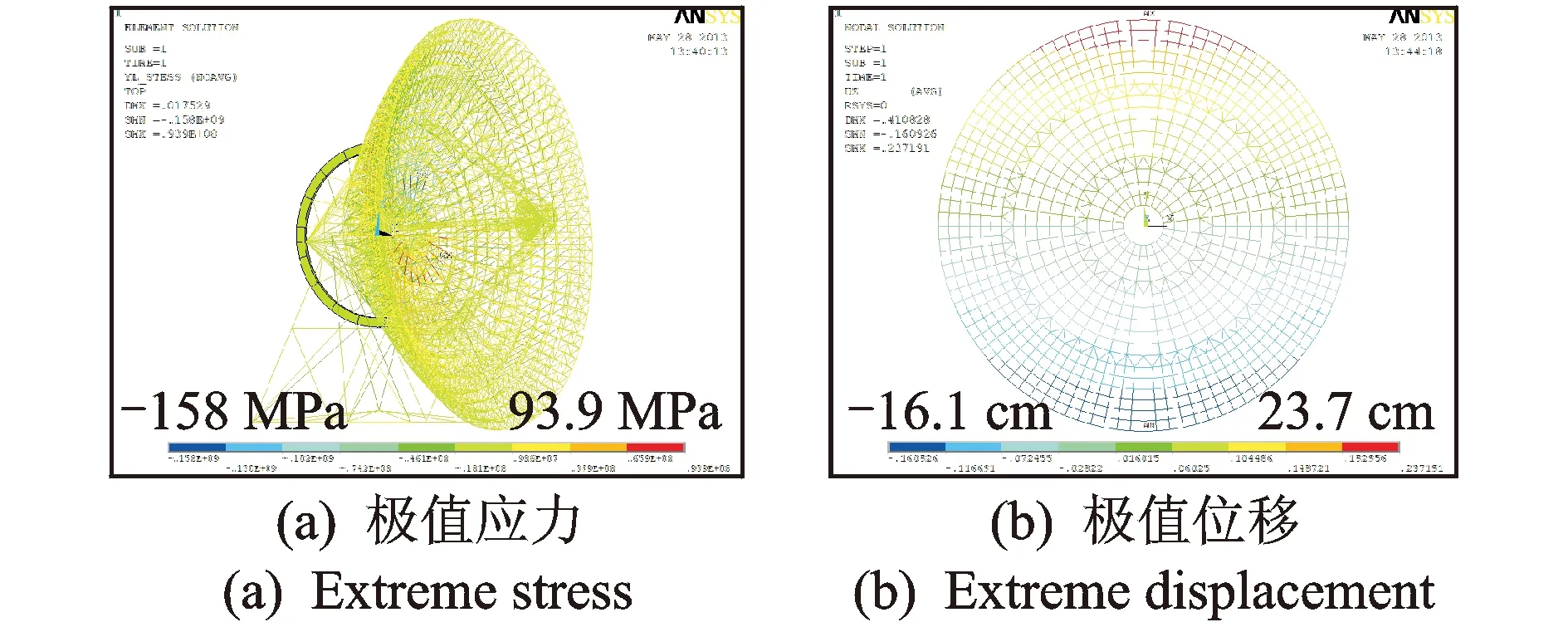
图20 5°俯仰角模型Fig.20 The 5°pitch angle model

图21 30°俯仰角模型Fig.21 The 30°pitch angle model

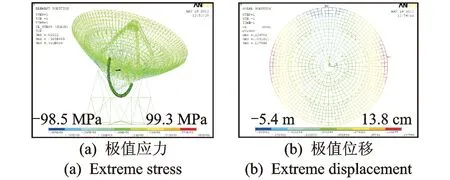
图22 60°俯仰角模型Fig.22 The 60°pitch angle model

Tab.4 Extreme response and wind vibration factors of the structure at different pitch angles

俯仰角/(°)最大位移/cm最大应力/MPa整体位移风振系数整体内力风振系数5241582.371.4130191741.731.546014991.821.5790221521.922.18

2) 从其功率谱密度函数可以看出，天线结构的风振响应是一个窄带过程。对于同一俯仰角模型而言，极值应力功率谱与位移功率谱在对结构的动力响应特征上呈现高度一致。结合前述结构自振频率，可以看出振动能量随着俯仰角的增大而逐渐提高，即高阶振型明显参与进来，开始对风致振动有所贡献。

3) 结合前述的静风效应分析得出的平均风压系数，以及动力非线性时程分析确定的各响应风振系数，可为天线结构抗风设计提供较为全面的风荷载取值。

[1] 刘岩，钱宏亮，范峰. 大型射电望远镜结构风荷载特性研究[J]. 红外与激光工程，2015，44(1)：148-156.

Liu Yan, Qian Hongliang, Fan Feng. Wind load characteristics of large radio telescope[J]. Infrared and Laser Engineering, 2015,44(1): 148-156. (in Chinese)

[2] 庞毅. 深空大天线结构设计关键技术[J]. 电子机械工程, 2011,27(3):28-30.

Pang Yi. Key technologies of large antenna mechanical design[J]. Electro-Mechanical Engineering, 2011,27(3):28-30. (in Chinese)

[3] Solari G, Piccardo G. Probabilistic 3-D turbulence modeling for gust buffeting of structures[J]. Probabilistic Engineering Mechanics, 2001, 16: 73-86.

[4] 刘彦，张庆明，黄风雷，等. 反射面变形对天线辐射特性的影响[J]. 北京理工大学学报, 2004,24(6):541-545.

Liu Yan, Zhang Qingming, Huang Fenglei, et al. Influnence of distortion of a shaped beam reflector on the radiation characteristics of an antenna[J]. Transaction of Beijing Institute of Technology, 2004,24(6):541-545. (in Chinese)

[5] Storrie-Lombardi M C, Irwin M J, Hippel T V, et al. Spectral classification with principal component analysis and artificial neural networks[J]. Vistas in Astronomy, 1994, 38(3): 331-340.

[6] Gawronski W, Mellstrom J A, Bienkiewicz B. Antenna mean wind torques: a comparison of field and wind-tunnel data[J].IEEE Antennas and Propagation Magazine, 2005, 47(5):55-59.

[7] Mahmoud M, Youssef M, Ali T. Unsteady computational and experimental fluid dynamics investigations of aerodynamic loads of large optical telescopes[J]. Computational Fluid Dynamics, 2010(1): 200-226.

[8] Polsky S. CFD prediction of airwake flowfields for ships experiencing beam winds[C]∥21st AIAA Applied Aerodynamics Conference. Orlando: AIAA, 2003.

[9] 杜强, 杜平安. 大气边界层中天线风荷载特性的数值分析[J]. 电子科技大学学报, 2010(2):170-171.

Du Qiang, Du Pingan. Numerical analysis for characteristics of wind loads on antennas in atmospheric boundary layer[J]. Journal of University of Electronic Science and Technology of China, 2010(2):170-171. (in Chinese)

[10]张亚林. 50米口径射电天线天线结构静动力分析[J]. 电子机械工程, 2004,20 (6): 37-40.

Zhang Yalin. The static and dynamic analysis of the 50m-diameter radio telescope antenna structure[J]. Electro-Mechanical Engineering, 2004, 20(6): 37-40. (in Chinese)

[11]张亚林, 刘维明. 50米射电天线天线座架结构动力设计[J]. 无线电通信技术, 2003 (5): 5-6.

Zhang Yalin, Liu Weiming. Dynamic design of 50m-diameter radio telescope antenna pedestal structure[J]. Radio Communications Techniques, 2003(5): 5-6. (in Chinese)

[12]钱宏亮, 刘岩, 范峰. 上海65m全可动天线结构变位疲劳作用分析[J]. 电波科学学报, 2012(11): 3027-3033.

Qian Hongliang, Liu Yan, Fan Feng. Rotational fatigue analysis on Shanghai 65 m fully steerable antenna structure[J]. Chinese Journal of Radio Science, 2012(11): 3027-3033. (in Chinese)

[13]张相庭. 工程抗风设计计算手册[M]. 北京: 中国建筑出版社, 1998: 20-23.

[14]Murakami S, Mochida A. Development of a new model for flow and pressure fields around bluff body [J]. Journal of Wind Engineering and Indusrial Aerodynamics, 1997(67/68): 169-182.

[15]林斌. CFD模拟技术在大型复杂结构工程中的应用[D]. 哈尔滨：哈尔滨工业大学, 2005.