基于应变的变形副反射面位姿形貌快速重构方法∗
2020-09-28王从思易乐天
许 谦 王从思 易乐天
(1 中国科学院新疆天文台乌鲁木齐830011)(2 中国科学院射电天文重点实验室乌鲁木齐830011)(3 西安电子科技大学电子装备结构设计教育部重点实验室西安710071)
1 引言
随着科学技术的不断进步, 反射面天线日益广泛地应用在天文观测、雷达与卫星通信等方面. 其中, 大型双反射面天线因其增益高且结构简单的特点成为最常用的地面卫星通信站天线.
近年来卫星通信发展迅猛, 大型双反射面天线的口径、频段也在不断地增加, 对天线的指向精度、增益损失等技术指标的要求也越来越严格, 这给天线的结构设计带来了很多挑战. 然而, 为实现大口径、高频段双反射面天线的高灵敏度和高分辨率, 其方位座架需要能够对反射体部分进行方位俯仰的实时性调整, 这要求反射体部分的刚度不能过强, 否则将导致天线结构过于笨重. 与此同时, 在实际工作时天线需要长期暴露在自然环境中, 其反射体容易受到自重以及风荷、雨雪、太阳照射等环境因素的影响而产生变形, 其中副反射面的位姿和形貌很容易发生变化, 这会导致主副反射面位置匹配失调, 使天线的电性能逐步恶化, 如增益下降、指向偏离和副瓣电平升高. 因此, 如何快速、实时且更加精准地重构副反射面位姿、形貌, 对于提升大型双反射面天线工作性能有很重要的意义[1–7].
为了获取更精准的副面, 常用的方法是基于反射面天线机电耦合的思想, 通过远场方向图与口径场的相位误差来反推副面形貌. 文献[8]采用高效的射线追踪和新的插值方法来达到对副反射面更高精度的拟合, 文献[9]用Jacobi-Fourier全局展开式来表示成形的反射器表面. 区别于上述方法, 本文基于应变传感器和模态叠加原理, 分别通过采集天线发生变形后副反射面支撑腿、副反射面自身的应变值来重构副反射面的位姿、形貌[10–11].
2 副反射面位姿形貌重构
假设在副反射面支撑腿上按照一定的规律布置n个应变传感器, 应变传感器的测量值为εn×1= [ε1,ε2,···,εn]T, 且设副反射面支撑腿与副反射面连接处的节点个数为m,其中εn表示第n个应变传感器的测量值.
利用ANSYS软件对大型双反射面天线的结构有限元模型进行模态分析, 可以获得前N阶位移模态振型和前N阶应变模态振型, 且为了避免广义模态坐标矩阵奇异, 传感器数量应不小于截取模态数, 即nN. 并可以从中提取副反射面支撑腿与副反射面连接点处节点对应的位移模态振型矩阵βm×N以及副反射面支撑腿上应变传感器处节点对应的应变模态振型矩阵γn×N, 分别为:

其中,p1,p2,···,pm表示副反射面支撑腿与副反射面连接点处的节点,q1,q2,···,qn表示副反射面支撑腿上应变传感器处的节点,表示副反射面支撑腿与副反射面的第pm个连接点处节点的第N阶位移模态振型,γqn N表示副反射面支撑腿上第qn个应变传感器处节点的第N阶应变模态振型.
根据模态叠加原理, 载荷作用下副反射面支撑腿结构的应变可表示为各阶应变模态的线性组合, 从而可以利用最小二乘法反推出最优的广义模态坐标rN×1= [r1,r2,···,rN]T, 即求在欧几里得空间以2-范数作为距离, 使得模态矩阵γn×NrN×1与εn×1之间距离
最小的模态坐标rN×1, 如下式所示:

将(3)式平方后对广义模态坐标求导:

于是可以得到最优的广义模态坐标rN×1:

根据最小二乘法原理,数据量越大,系统参数估计的精度越高.当传感器的数量nN时,所求得的广义模态坐标rN×1比较准确. 重构结果受应变传感器读数误差影响的程度较低, 保证了位移重构的准确度.
同理, 载荷作用下副反射面支撑腿与副反射面连接处节点的位移也可表示为各阶模态的线性组合, 则该位移向量χm×1=[χ1,χ2,···,χm]T可表示为:

其中,χ1,χ2,···,χm表示副反射面支撑腿与副反射面连接点处的节点在x、y、z方向的位移.
假设双反射面天线的副反射面只发生刚体位移和刚体转动, 并以副反射面顶点为原点建立局部坐标系O-xyz, 且天线变形后副反射面的顶点坐标为(x′i,y′i,z′i)′, 其中i= 1,2,3,···,n表示双反射天线的n种不同变形, 结合变形前副反射面支撑腿与副反射面连接处的节点坐标(xi,yi,zi), 则可获得变形后连接点处的节点坐标(x′i,y′i,z′i). ∆x、∆y、∆z分别表示副反射面顶点变形前后在x、y、z方向上的平移分量. 根据变形前后连接处节点与副反射面顶点之间的相对距离不变, 即:

取3组变形前后连接处的节点坐标代入(7)式即可求得副反射面顶点变形前后的平移量∆x、∆y、∆z.
假设在坐标系O-xyz中副反射面处于初始指平状态, 其几何示意图如图1所示, 则变形前后副反射面支撑腿与副反射面连接处节点坐标之间的关系是:

式中,

其中,φ、ϑ分别为副反射面绕z轴、x轴右手转动的角度.

图1 副反射面坐标系示意图Fig.1 Sketch of subreflector coordinate system
综上, 变形后副反射面的位姿是由变形前的副反射面经过平移量∆x、∆y、∆z与转动量φ、ϑ得到的. 在外载荷作用下, 发生变形的大型双反射面天线, 可以利用副反射面补偿技术即通过调整副反射面位置、姿态来进行主面变形补偿时, 上述结果可以与由主面变形后的最佳吻合抛物面求得的副反射面顶点位置相结合[12], 有助于获得更精准的最佳副反射面位置, 实现主副反射面之间的最佳匹配调整.
与上述方法中通过采集副反射面支撑腿上的应变值来计算天线发生变形后副反射面支撑腿与副反射面连接处位移的工作原理相同, 在副反射面结构上选择一定数量的特征点并布置应变传感器, 并基于模态叠加原理可以获得副反射面上一系列离散特定目标节点处的位移. 当利用副反射面补偿技术, 可以通过分片可调的副反射面来更精确地消除主反射面变形造成的光程差, 优化天线口径场幅度和相位分布[13].
3 模型仿真
以某大型双反射面天线进行实例分析, ANSYS结构模型如图2所示.
在副反射面支撑腿结构中共布置了16个应变传感器, 其分布位置如图3所示, 图中应变传感器的位置为对应的单元中点. 如果考虑到大空间跨度温度梯度以及传感器的测量误差等因素时, 传感器应布置于距离副面较近的地方.
并且, 副反射面结构上应变传感器和目标点的位置分布分别如图4、5所示.

图2 ANSYS结构模型示意图Fig.2 Schematic diagram of ANSYS structural model

图3 支撑腿应变传感器分布示意图Fig.3 Schematic diagram of strain sensor distribution on supporting legs

图4 副反射面应变传感器分布示意图Fig.4 Schematic diagram of strain sensor distribution on subreflector

图5 副反射面目标点分布示意图Fig.5 Distribution of target points on subreflector
4 结果分析
通过ANSYS软件对理想情况下的天线模型施加重力载荷, 并进行网格划分和模态分析. 通过(3)式、(4)式, 计算出天线支撑腿与副反射面连接点处的节点位移, 将应变传感器测量的应变数据计算得到的位移与提取出来的ANSYS有限元法计算位移进行比较,两种测量的对比结果如表1所示.
同理, 可以通过在副面布置应变传感器来计算副面目标节点位移, 由于所选目标节点数目多, 为便于分析, 本文只对副反射面z轴方向目标节点位移数据进行对比, 如表2所示,x、y轴方向的目标节点位移如表3所示.
根据模态叠加原理计算的目标节点位移, 除个别点位移误差较大之外, 其他均在10%以内, 在可接受的误差范围内, 满足精度要求, 说明双反射面天线在外载荷下, 使用应变传感器和模态叠加原理计算得到的目标点位移满足精度的要求. 副反射面平动、转动参数分别如表4、表5所示.

表1 两种方法测量天线支撑腿与副面连接点处节点位移Table 1 The node displacement at connection points between antenna supporting legs and subreflector calculated by two methods
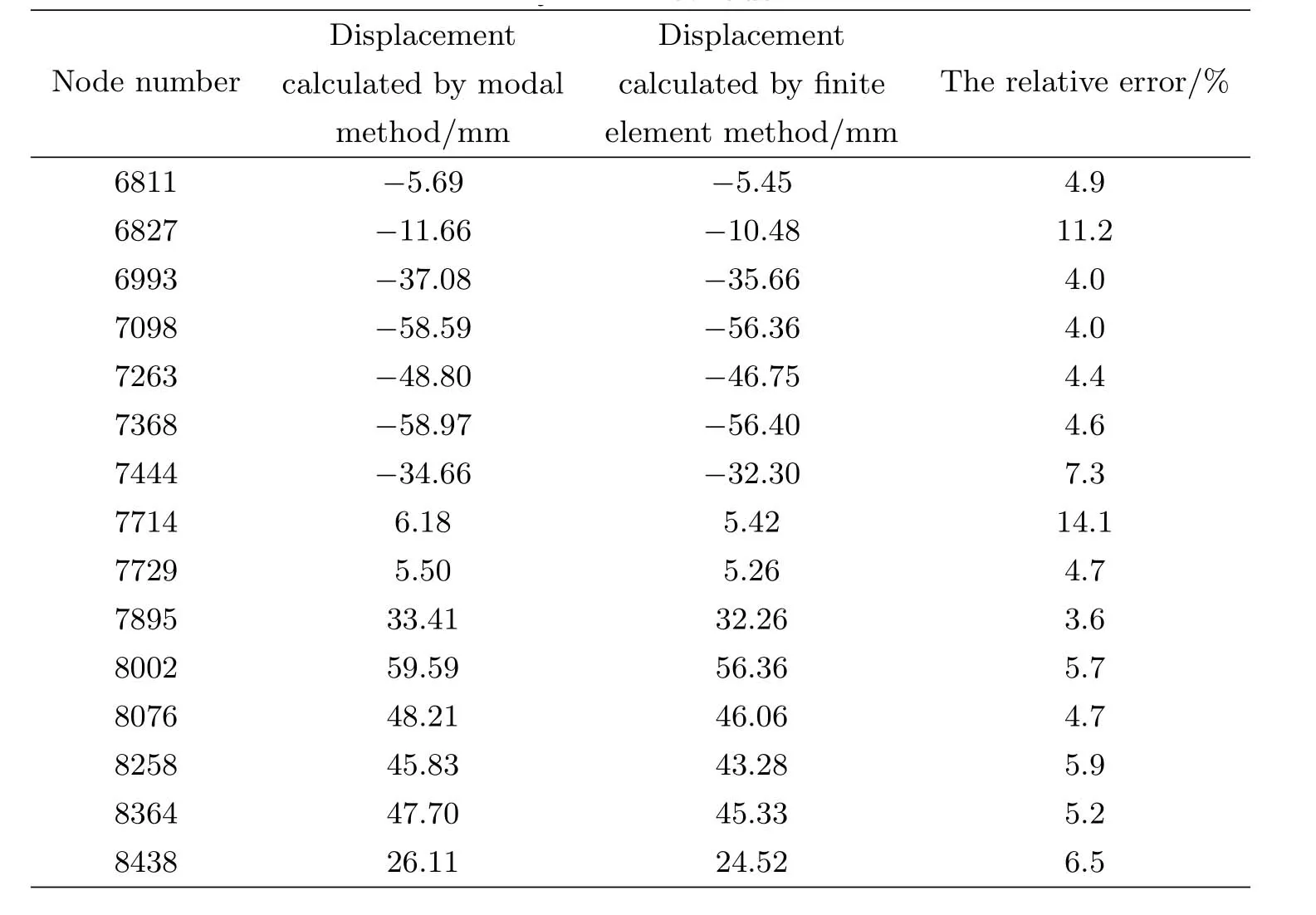
表2 两种方法测量副面z轴方向目标节点位移表Table 2 The displacement of target node in z axis of subreflector calculated by two methods
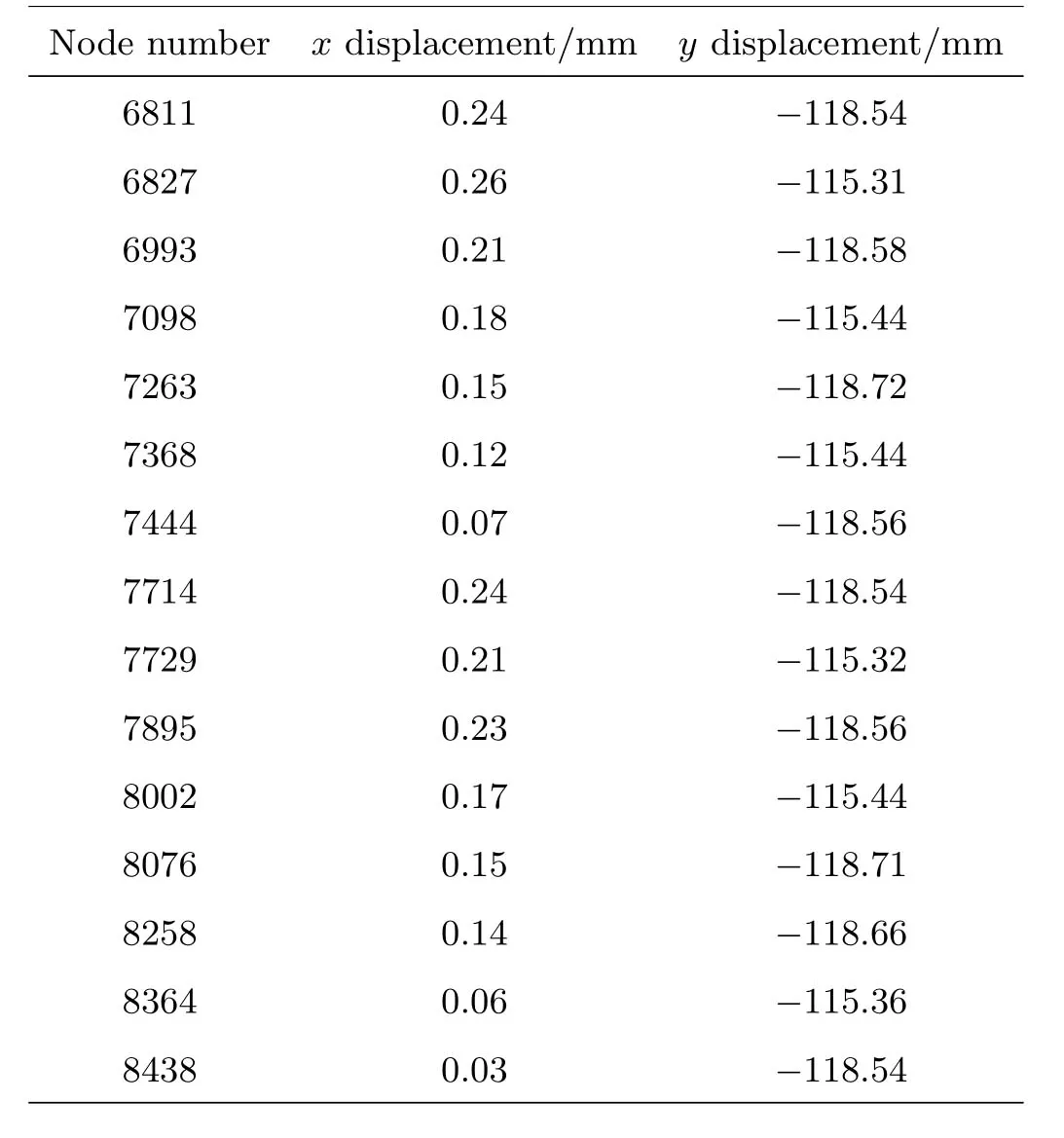
表3 副面x、y轴方向目标节点位移Table 3 The displacement of target nodes in the x, y axes of the subreflector

表4 副反射面平动参数Table 4 The translational parameters of the subreflector

表5 副反射面转动参数Table 5 The rotation parameters of the subreflector
5 结束语
本文研究了基于应变的变形副反射面位姿形貌快速重构方法, 该方法的先进性在于即使大型双反射面天线的结构载荷信息未知, 也可以通过这种方法, 利用少量应变传感器测量的应变值, 快速、准确地重构出变形后副反射面的位姿、形貌, 该方法步骤简单,容易实现, 结果精确. 特别是针对副反射面受到重力作用发生下垂变形的情况, 因为重力是造成副反射面姿态变化的主要因素. 通过结合案例建模仿真, 将使用该方法算出来的目标节点位移与ANSYS有限元法计算出来的位移相对比, 两者之间的误差满足精度要求, 证实了该方法的有效性. 实际工程中, 只需应用此坐标系与实际工程中指定坐标系之间的转换关系即可获得实际工程所需的平移和转动关系, 并且可以预先计算天线在不同工况下的副反射面相关调整数据并存入数据库以实现对副反射面的实时修正, 从而保证天线在不同工况下都能获得最佳的观测效率.
