由激光辐照固体表面引起的非Fourier三维传热问题的解析解

张丽静， 尚新春

(北京科技大学 数理学院，北京 100083)



由激光辐照固体表面引起的非Fourier三维传热问题的解析解

张丽静， 尚新春

(北京科技大学 数理学院，北京 100083)

针对激光束瞬间加热物体表面时，材料表面附近温度场变化的问题，建立了基于非傅里叶热传导理论的三维热传导数学模型. 考虑了激光束的聚焦特征，即热量或高温主要集中在光束中心附近的局部区域，且沿材料表面切向呈非均匀分布. 利用积分变换技巧，得到了问题Laplace逆变换的解析形式，从而给出了新的温度场解析解，并据此分析了传热过程中固体内部的温度场演化规律及特征. 数值计算结果显示，该问题的温度场呈现出明显的非傅里叶传热特征，与经典的热传导的扩散形式不同，它是以波的形式进行传热的.

激光辐照；热波效应；非傅立叶热传导；积分变换解析解

激光材料表面处理技术是一种现代材料加工过程中的常用方法[1]. 由于激光具有能流密度高且容易聚焦的特点，激光束辐照的物体表面温度分布主要集中在光束中心附近，辐照对材料的影响仅限于局部区域[2]，故该处理方法可将对材料的影响限制在一个较小的局部区域. 深入分析材料表面在局部受热时的热传导过程，对提高材料表面处理水平具有重要的意义. 由于激光辐照时间短，热源密度很大，此类传热问题中热量往往是以“热波”形式传导的，这便是非Fourier传热效应[3].

基于非Fourier传热数学模型的研究已有许多成果. 由于非Fourier传热在解析求解方面存在很大的困难，很多学者采用了数值的方法来寻求问题的数值解. 常用的数值方法主要有差分法[4]、有限元法[5-6]、有限体积法[7]等. 对解析解的研究则大多数局限于空间一维的问题[8-10]，即表面受均匀分布热源加热的物体内瞬态温度场的一维解，但该解并不能较为准确地用于激光束辐照材料表面时材料内温度场的分析.

针对激光束辐照的实际情况，考虑到激光束的聚焦特征，可设激光束加热物体表面时，其温度沿径向负指数衰减并呈轴对称分布. 考虑到热量分布的对称特性，利用柱极坐标系，该问题可转化为一个物体内部温度的二维空间瞬态响应问题.

基于非Fourier热传导热波理论，应用积分变换方法可以给出该问题积分形式的解析解，从而可据此分析非Fourier传热效应. 应该指出的是，在应用积分变换求解时，一般难以精确地给出积分逆变换的解析结果，大多采用数值方法进行逆变换，而本文得到了问题Laplace逆变换的解析形式，使问题的求解大为简化. 此外，通过与基于经典热传导理论稳态和非稳态结果相比较，非Fourier效应可被清晰呈现.

1 数学模型及积分变换

考虑激光束垂直辐照在半无限大物质表面时的传热问题. 由于激光束会在材料表面产生一定的能量沉积，故在物体表面会出现一薄层热源. 当激光透射深度很小时，可将热源简化为物体表面给定温度的情形. 若采用柱极坐标系(r，φ，z)，则由问题的轴对称性知温度场T与环向坐标φ无关，即T=T(r，z，t)(r≥0，z≥0，t≥0)，其中：r为与竖直坐标轴水平距离的变量；z为材料内的点到材料表面距离的变量；t为时间的变量.

非Fourier传热的温度场控制方程为[11]

(1)

式中：τ0为材料的松弛时间；γ=ρ0c0/k0为材料的导温系数之倒数，ρ0为材料的密度，c0为材料的比热，k0为热传导系数.

激光辐照使物体表面突然加热，并可设其表面温度沿径向负指数衰减，故边界条件可描述为

(2)

式中：H(t)为Heaviside阶跃函数；p>0为表面温度的衰减常数；Tc为辐照激光束的最高温度. 激光束在材料表面的温度分布如图1所示.

另外，温度场的轴对称性条件及无限远处条件为

(3)

设初始时物体内无温度变化，则初始条件为

(4)

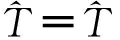
(5)

边值条件(2)及(3)中最后一个条件变换后为

(6)

利用条件(6)可得式(5)的解为

(7)

原问题的解可以通过如下逆Hankel变换和逆Laplace变换表示为

(8)

2 激光表面辐照问题的解析解

由于式(7)的逆Hankel变换不易解析求出，将表达式(8)中两个逆变换交换次序.

(9)

式(9)中逆Laplace变换的解析结果为

(10)

其中

(11)

且

原问题的解析解为

(12)

经典Fourier热传导理论问题的解，可令式(7)中的松弛时间τ0=0. 此时，去掉式(4)中最后一个初始条件，式(7)化简为

(13)

其Laplace逆变换为

(14)

其中

基于经典Fourier热传导理论问题的解析解为

(15)

对于稳态情形的解，可在式(7)中令γ=0，同理可得原问题的稳态解为

(16)

3 温度场的非Fourier效应

作为数值算例，考虑当激光辐照在半无限大体表面时，材料内温度的空间分布和随时间变化的情况. 对基于非Fourier理论(τ0取0.03，0.08)、经典热传导理论(τ0=0)和稳态情形(γ=0)的温度场解(12)(15)(16)分别进行数值计算. 其他参数分别取为ρ0=2 770 kg/m3，c0=921 J/(kg·K)，k0=120 W/(m·K)，p=1 000.

图2给出了材料内部距辐照中心深度为1 mm处，从辐照开始到0.5 s，量纲一温度T(r，z，t)/Tc的变化曲线. 从图2明显看到与经典理论所得温度不同的是: 基于非Fourier热传导理论的温度，在初始的短暂时间内保持为0，这是由于松弛时间τ0的影响而呈现出的传热滞后效应. 随后温度突增，达到峰值后迅速下降，再逐渐趋于稳态解. 松弛时间τ0越大，达到温度峰值所需的时间也越长，峰值温度也越高. 因此，温度的非Fourier理论解与经典理论解在初始瞬间的性态上存在较大的差异. 这说明文中给出的解析解能够很好地反映激光辐照问题所具有的非Fourier效应.

图3(a)给出了松弛时间τ0=0.03时量纲一温度T/Tc在不同时刻沿z轴(r=0)变化的曲线. 由图3(a)可以看出：由于非Fourier传热效应，温度以热冲击波的形式向深度方向传播. 例如，热波传播前沿(间断面)在0.01，0.05，0.11 s时深度分别达到0.4，2.0，4.4 mm. 热波前沿的运行速度约为40 mm/s. 热波传播前沿的温度呈现局部峰值，随着时间的增加，前沿温度逐渐减小，且温度沿z轴的分布曲线趋于稳态解的曲线. 而由经典Fourier传热理论所得温度是以无限速率沿深度方向扩散、衰减至0的，如图3(b)所示. 在同一深度温度随时间的增加而增高，并且逐渐趋于稳态情形. 这说明非Fourier理论解在传播形式和空间分布上与经典理论解有着本质的不同.

图4给出了T/Tc=1/4等温线在不同辐照时间时的空间位置. 随着时间的增加，由经典传热理论(τ0=0)得到的等温线逐渐向深处移动，并趋向于稳态情形的等温线，而非Fourier传热理论(τ0=0.03)所给出的等温线则向相反方向移动，但亦趋向于稳态情形. 在辐照开始的瞬时，两者温度的空间分布存在很大差异，但是这种差异随着时间的增加而逐渐变小. 因为激光辐照是以热冲击的形式，将物体表面突然加热到一个恒定的温度，故在辐照开始的瞬时，热波效应较为明显.

图5给出了τ0=0.03，t=0.01，t=0.03和t=0.07 s时温度场在材料内部的分布. 过z轴(垂直)纵剖面上的温度场解析解，可以清晰地展现出导热的非Fourier效应，即显示出热传播的“热波”特征. 易见，材料内部给定点处的温度， 在热波前峰面到达之前并没有受到材料表面温度变化的影响，而在热波前峰面抵达后则出现了一个较为显著的升高，并在热波峰面经过后开始逐渐回落，最终达到其稳定状态. 这一结果与基于传统的傅里叶热传导理论所建立的数学模型有明显的不同. 传统傅里叶热传导问题的解显示，在材料表面温度提高时，材料内部各点温度也会同时升高，热在材料内部的传播速度是无穷大，热的传播并不表现出“热波” 特征，而是以“扩散”形式进行传播的.

4 结 论

针对激光束瞬间照射半无限大材料表面而引起内部温度变化的问题，建立了一种基于非傅立叶热传导理论的三维热传导数学模型，并考虑了激光光源能量密度的分布特征. 由于实际问题具有空间轴对称的特性，从数学上看，分析了材料表面辐照的非均匀性及二维空间的传热. 利用Laplace变换和Hankel变换及其逆变换，选择了适当的积分顺序及变量替换，给出了含有松弛时间的双曲型热传导方程单积分形式的解析解，从而给出材料内部温度场分布的单积分形式解析解. 数值仿真的结果显示，该解析解能清晰地反映出非傅立叶热传导理论中出现的“热波”现象，同时也说明非傅立叶热传导理论与传统的傅立叶热传导理论有着本质的不同.

[1] Yilbas B S， Al-Dweik A Y. Closed form solutions for thermal stress field due to non-equilibrium heating during laser short-pulse irradiation[J]. Physica B: Condensed Matter， 2012，407(12):2169-2175.

[2] Yilbas B S， Kalyon M. Analytical solution for pulsed laser heating process: convective boundary condition case[J]. International Journal of Heat and Mass Transfer， 2002，45(7):1571-1582.

[3] Maurer M J， Thompson H A. Non-Fourier effects at high heat flux[J]. International Journal of Heat and Mass Transfer， 1973，92(2):284-286.

[4] Carey G F， Tsai M. Hyperbolic heat transfer with reflection[J]. Numerical Heat Transfer， 1982，5(3):309-327.

[5] Loh J S， Azid I A， Seetharamu K N， et al. Fast transient thermal analysis of Fourier and non-Fourier heat conduction[J]. International Journal of Heat and Mass Transfer， 2007，50(21-22):4400-4408.

[6] Tamma K K， Railkar S B. Specially tailored transfiniteelement formulations for hyperbolic heat conduction involving non-Fourier effects[J]. Numerical Heat Transfer Part B， 1989，15(2):211-226.

[7] Mishra S C， Sahai H. Analyses of non-Fourier heat conduction in 1-D cylindrical and spherical geometry-an application of the lattice Boltzmann method[J]. International Journal of Heat and Mass Transfer， 2012，55:7015-7023.

[8] Lam T T， Fong E. Application of solution structure theorem to non-Fourier heat conduction problems: analytical approach[J]. International Journal of Heat and Mass Transfer， 2011，54(23-24):4796-4806.

[9] Yilbas B S， Al-Aqeeli N. Analytical investigation into laser pulse heating and thermal stresses[J]. Optics & Laser Technology， 2009，41(2):132-139.

[10] Ahmadikia H， Fazlali R， Moradi A. Analytical solution of the parabolic and hyperbolic heat transfer equations with constant and transient heat flux conditions on skin tissue[J]. International Communications in Heat and Mass Transfer， 2012，39(1):121-130.

[11] Andarwa S， Tabrizi H B. Non-Fourier effect in the presence of coupled heat and moisture transfer[J]. International Journal of Heat and Mass Transfer， 2010，53(15-16):3080-3087.

(责任编辑：刘雨)

Non-Fourier Effect in Three-Dimensional Heating Conduction by Laser Irradiation on Surface

ZHANG Li-jing， SHANG Xin-chun

(School of Mathematics and Physics， University of Science and Technology Beijing， Beijing 100083， China)

To the heat conduction problem rising as laser beam irradiating on the metallic surfaces, a three dimensional mathematical model was established based on non-Fourier heat conduction theory for thermal distribution near the surface of material. The focusing property of laser beam was considered, that the high temperature mainly focus in a local area around the center of the laser beam and distributes non-uniform in direction along the surface. Based the techniques of integral transform, the analytic solution of the problem in form of inverse Laplace transform was derived and the patterns and characters of the thermal field were analyzed based on the two dimensional analytic solution. The numerical solutions show that the thermal field has clear property of non-Fourier heat conduction. Being different from the classical thermal conduction, the heat travels with waveform in the material.

laser irradiation; heat wave effect; non-Fourier heat conduction; analytic solution of integral transformation

2015-01-15

国家自然科学基金资助项目(10772024)；北京理工大学爆炸科学与技术国家重点实验室开放基金(KFJJ12-12M)

张丽静(1973—)，女，博士生，E-mail:zhanglij@ustb.edu.cn.

尚新春(1958—)，男，教授，博士生导师，E-mail:shangxc@ustb.edu.cn.

O 39

A

1001-0645(2016)08-0876-05

10.15918/j.tbit1001-0645.2016.08.018