固定翼鸭舵式双旋弹的制导控制算法研究
2016-11-21张衍儒肖练刚
张衍儒,肖练刚,周 华,曹 莹
(1.北京航天自动控制研究所,北京 100854; 2.中国人民解放军第四五六医院,山东 济南 250031)
固定翼鸭舵式双旋弹的制导控制算法研究
张衍儒1,肖练刚1,周 华1,曹 莹2
(1.北京航天自动控制研究所,北京 100854; 2.中国人民解放军第四五六医院,山东 济南 250031)
从降低制导武器成本和体积的角度出发,在GPS接收机和x轴陀螺仪等少量信息的基础上,根据双旋弹的抛物线飞行特性,提出一种基于调整固定翼鸭舵控制力矢量方向进行弹道修正的制导算法。此种制导方式并不需要精确的弹体姿态信息,通过GPS接收机数据估算弹体的当前姿态,并通过弹体的静稳定裕度保证飞行稳定性,实现落点偏差的有效修正。最后在分析姿态信息采集算法的误差范围的基础上,对制导控制算法的适用性进行了分析与验证。
自动控制技术 ;固定翼鸭舵;双旋弹;制导控制;姿态信息采集
固定翼鸭舵式双旋制导迫击炮弹[1-3]相对于十字鸭舵式制导迫击炮弹[4]的优势在于:简化十字鸭舵为固定舵角的固定翼鸭舵,降低了控制舱成本和体积;利用斜切尾翼带动弹体旋转,利用鸭舵舵片带动鸭舵旋转,通过弹体与鸭舵之间的相对旋转发电提供控制舱的电能;仅利用GPS接收机和x轴陀螺仪,根据迫击炮弹的静稳定性,实现迫击炮弹的姿态信息采集。
在未知风速的条件下,利用GPS接收机和x轴陀螺仪等少量信息,提出一种基于调整固定翼鸭舵控制力矢量方向进行弹道修正的制导算法用于固定翼鸭舵式双旋制导迫击炮弹的落点修正,并在分析姿态信息采集算法的误差范围的基础上,对制导控制算法的适用性进行了分析,验证了此种制导控制算法适用于固定翼鸭舵式双旋制导迫击弹。
1 双旋弹的制导控制原理
基于十字鸭舵的六自由度控制方式,虽然可以精确实现横、法向过载修正,但是整体设计成本较高,固定翼鸭舵式双旋弹从降低制导迫击炮弹控制舱成本和体积的角度出发,简化十字鸭舵为固定舵角的固定翼鸭舵[5],固定翼鸭舵的一对舵片用于提供鸭舵绕弹体纵轴反向旋转的导转力矩,图1为双旋弹的绕质心运动,其中滚转舵片1、3,俯仰舵片2、4用于提供弹体绕质心运动的控制力矩。

固定翼鸭舵通过内部的轴承绕弹体纵轴旋转,当固定翼鸭舵的滚转角速度为零时,固定翼鸭舵相对弹体纵轴静止。此时固定翼鸭舵的俯仰舵片产生鸭舵气动控制力,考虑绕质心运动,可以得到鸭舵气动控制力矩。由于双旋弹为静稳定弹,因此弹体压心在质心后,考虑弹体绕质心的动力学方程,可知弹体静力矩和鸭舵气动控制力矩能够满足力矩平衡条件,使双旋弹产生相应的合成攻角,考虑全弹质心运动的动力学方程,可知弹体纵轴向鸭舵气动力矢量方向移动,根据上述原理实现双旋弹的制导飞行控制。
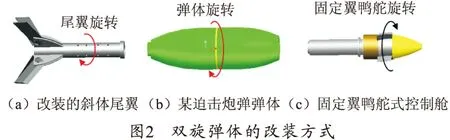
为了进一步降低控制舱的成本和体积,改装迫击炮弹的群式尾翼为斜切尾翼,用于提供导转力矩带动弹体旋转,改进弹体为双旋弹体,如图2所示。
为了保证双旋弹的弹道能够按照抛物线方式命中目标点,需要保证双旋弹为静稳定弹,双旋弹的稳定性可以用稳定储备量T来表示:
(1)
式中:XF表示双旋弹焦点至弹头的距离;Xg表示双旋弹质心至弹头的距离;bA表示弹翼的平均气动弦长,可取全弹长度。
由于双旋弹质心位置Xg和焦点位置XF的计算误差,需要在确定稳定度时留一定余量。焦点位置误差可取
ΔXF≈0.005LB~0.01LB
(2)
式中,LB为双旋弹全弹长度。
由于迫击炮弹前端安装了固定翼鸭舵,降低了迫击炮弹的静稳定性,为综合平衡上述这些影响,并留有一定余量,稳定储备量T的取值范围为8%~20%,即
0.08LB≤XF-Xg≤0.2LB
(3)
-0.2CLαLB≤Cmα+xcScCNδ≤-0.08CLαLB
(4)
式中:Cmα表示弹出式尾翼和弹体的静力矩系数; xcScCNδ表示固定翼鸭舵的静力矩系数;CLα表示弹体的升力系数。
利用式(4)计算弹出尾翼的稳定储备量为11.1%~16.8%,满足稳定储备量8%~20%之间的要求,其阻力和升力特性也均满足使用的要求,弹出尾翼可以根据不同的后掠角和展弦比,调整双选弹稳定储备量T大小,因此可以通过设计合理的弹出尾翼作为双旋弹的稳定装置,保证双旋弹的飞行稳定。
从降低成本的角度,取消六自由度IMU惯组模块的安装,根据双旋弹的静稳定性,利用GPS接收机提供的速度信息近似计算弹体的俯仰和偏航姿态角,并利用x轴陀螺仪采集固定翼鸭舵绕弹体纵轴的角速率,实现双旋弹绕质心运动的三自由度姿态信息采集。
根据上述改进措施,利用GPS接收机、x轴陀螺仪、固定翼鸭舵和双旋弹体设计了双旋弹的控制系统,实现了双旋弹的落点偏差修正。
2 双旋弹绕质心三自由度信息采集
为实现双旋弹的制导飞行控制,利用GPS接收机和x轴陀螺仪实现双旋弹质心运动和绕质心运动的信息采集。
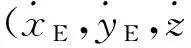
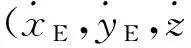
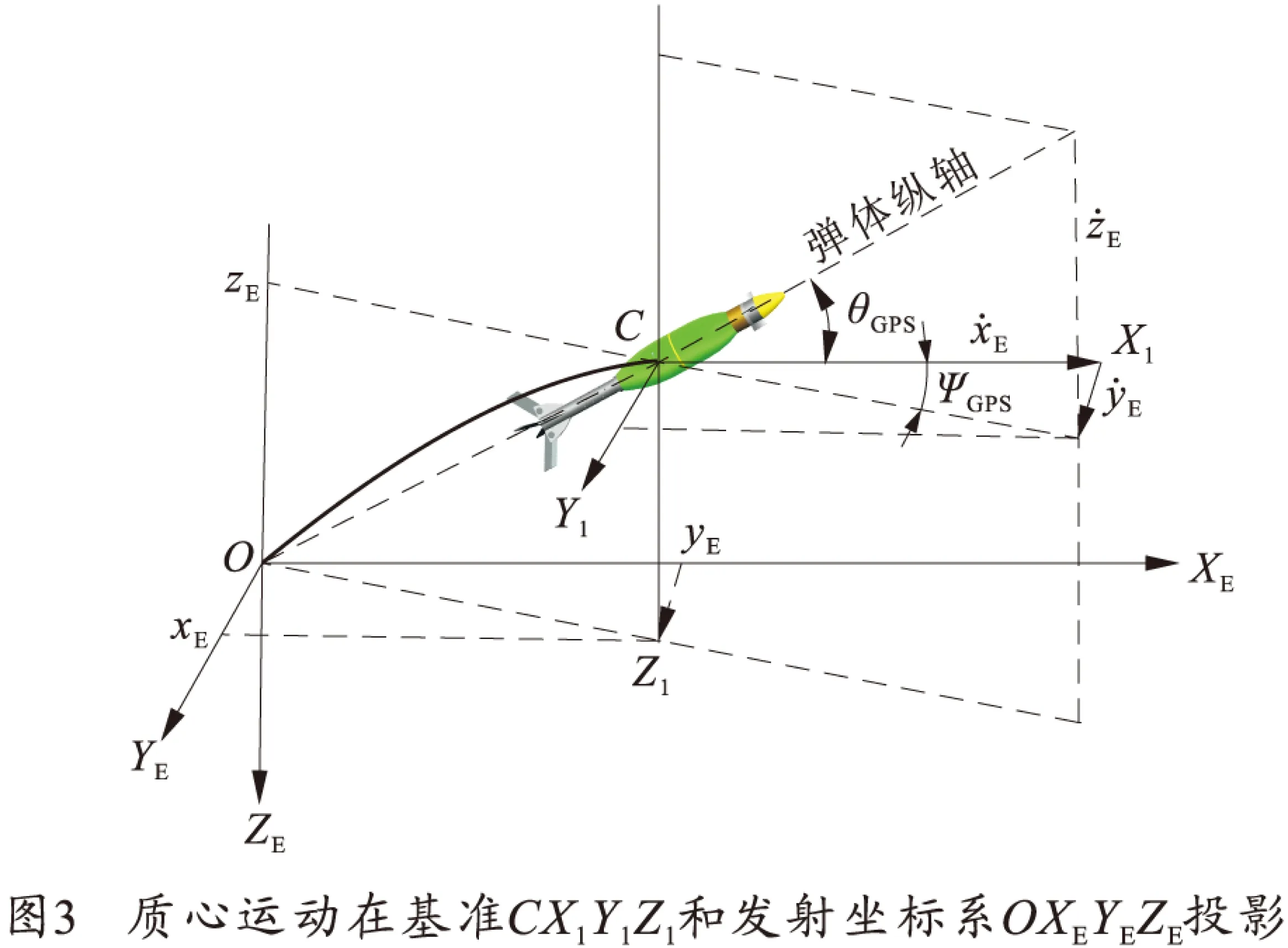
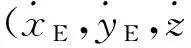
速度偏航角ψGPS和速度俯仰角θGPS求取公式如下:
(5)
当攻角和侧滑角为极小值时,弹体的速度轴和弹体纵轴重合,因此弹体在基准坐标系下的俯仰角θ和偏航角ψ,与通过GPS接收机计算得到弹体在基准坐标系下得到的俯仰角θGPS和速度偏航角ψGPS一致。
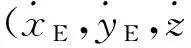
飞行控制过程中,需要实时测量固定翼鸭舵在弹体固定坐标中的滚转姿态,因此在弹体头部安装x轴陀螺仪,随固定翼鸭舵同步旋转,用于测量固定翼鸭舵的滚转角速度。鸭舵绕弹体纵轴转动的运动学方程如下:
(6)
综上所述,由于双旋弹为静稳定弹,因此并不需要精确的弹体姿态用于稳定控制,利用GPS接收机和x轴陀螺仪模块便可以实现双旋弹绕质心的三自由度信息采集。
3 姿态信息采集算法的误差分析
姿态测量主要利用GPS速度和陀螺角速度信息获取,其中GPS的采样周期为20 ms,可以通过卡尔曼滤波算法滤除GPS定位白噪声对姿态采集算法的影响,具体方法可以参考文献[6]中滤波算法的介绍,通过滤波算法计算后可以保证通过GPS求取的姿态误差在 2°以内,由于笔者设计的制导算法并不需要精确的姿态信息,能够体现姿态的变化趋势即可实现制导控制,因此通过GPS近似采集姿态信息可以满足本文的设计需要。
当利用x轴陀螺仪采集鸭舵的滚转角速度信息时,如果陀螺仪量程设定较大,则鸭舵的转速可调节范围越大,鸭舵的转角调节时间就越短,但是考虑陀螺仪测量角速度的精度随量程增大而成比例降低的影响,为保证角速度精度满足0.06(°)/s(50 s飞行时间累计误差3°)的精度指标,因此选用量程范围为±2 000 (°)/s、分辨率为216次和抗瞬时大过载的陀螺仪作为姿态测量系统,由于陀螺仪全程累积误差不超过3°,因此对姿态采集算法的影响较小,可以近似忽略。
由于双旋弹为静稳定弹,具有良好的追随稳定性,因此弹体纵轴与飞行速度矢量之间的合成攻角幅值应该小于追随攻角δpm,一般δpm的取值范围为12°~15°。由上述可知,双旋弹绕质心三自由度信息采集算法中偏航角ψGPS、俯仰角θGPS与实际偏航角ψ、俯仰角θ之间的最大误差为追随攻角δpm。
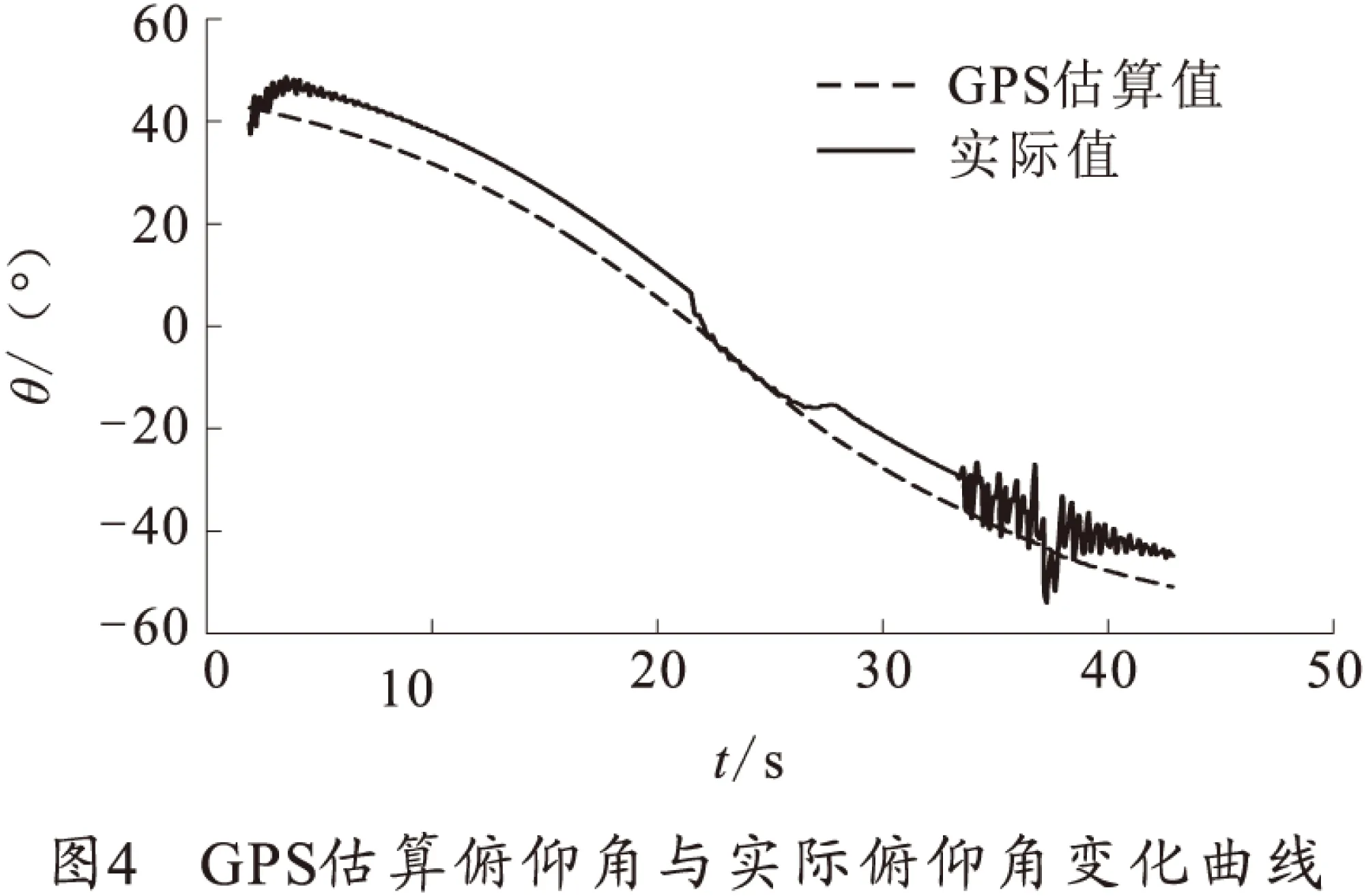
利用六自由度弹道方程编写仿真软件,计算制导控制过程中姿态信息采集算法的估算误差范围。GPS估算俯仰角与实际俯仰角变化曲线如图4所示,GPS估算俯仰角θGPS与实际俯仰角θ之间的误差范围为0°~11.5°,符合追随攻角δpm的变化范围。
GPS估算偏航角与实际偏航角变化曲线如图5所示,GPS估算偏航角ψGPS与实际偏航角ψ之间的误差范围为0°~13.542°,同样符合追随攻角δpm的变化范围。

4 调整鸭舵控制力矢量的制导算法


(7)
式中:vMx,vMy,vMz表示弹体在目标坐标系中的飞行速度;xT,yT表示目标点的坐标。
(8)
目标坐标系中速度的模值VM为
(9)
目标系中高低角λD和方向角λT的定义如图6所示。


(10)
定义视线坐标系,原点位于弹体质心M,MXT轴指向目标点方向,MZT轴垂直于MXT轴并且方向向下,MYT轴根据右手定则由MXT轴和MZT轴的指向确定。
(11)
(12)
式中:kψ,kφ为制导控制参数,为正数;m为双旋弹的全弹质量。
双旋弹抛物线弹道上升段时,固定翼鸭舵的目标滚转角为
(13)
下降段时,固定翼鸭舵的目标滚转角为
(14)
当鸭舵绕弹轴滚转角φN和目标滚转角φCMD一致时,鸭舵控制力矩能够使弹体纵轴的指向位置靠近目标落点,从而修正迫击炮弹的落点偏差。
5 制导算法的适用性仿真验证
利用六自由度弹道方程编写仿真软件,仿真制导算法的鸭舵滚转角、预测落点偏差、攻角和弹道曲线,初始条件为发射初速300 m/s,射角45°,风速范围为6级强风10.8~13.8 m/s,目标落点为射向7 km,横向为0 m,高度与发射点同一水平高度。
制导算法的修正过程较为平滑,如图7中预测落点曲线中射向偏差和横向偏差曲线在制导算法的修正下逐渐收敛到0,验证了制导算法可以满足双旋弹的弹道修正。

如图8所示,制导算法能够利用双旋弹的静稳定特性,保证双旋的飞行稳定,并且保证飞行姿态的估算误差小于追随攻角δpm。

6 结束语
根据双旋弹的抛物线飞行特性,笔者提出一种基于调整固定翼鸭舵控制力矢量方向进行弹道修正的制导算法,此种制导方式并不需要精确的弹体姿态信息,能够利用双旋弹的静稳定特性包容姿态信息的估算误差,在制导过程中有效修正双旋炮弹的落点偏差。在弹道模型中模拟双旋弹的实际飞行状态,通过仿真验证了该制导算法的适用性和可行性。
References)
[1]BURKE P, PERGOLIZZI A. XM1156 precision guidance kit (PGK) overview[C]∥The 53rd Annual Fuze Confe-rence. US: NDIA, 2009:12-15.
[2]YOUSEF H. Roll control guided mortar (RCGM)[C]∥Presentation at NDIA Joint Armaments Conference. Seattle: NDIA Joint Armaments Conference, 2012:14-17.
[3]ASAD K. Project overview-precision air dropped guided munition(PADGM)[C]∥46th Annual Gun & Missile Systems Conference & Exhibition. USA:NDIA, 2011:1-7.
[4]COLONEL Ole Knudson. Cannon artillery and mortar cannon artillery and mortar precision effects[R]. Combat Ammunition Systems, 2003.
[5]CLANCY J A, BYBEE T D, FRIEDRICH W A.Fixed canard 2-D guidance of artillery projectiles, US, US6981672B2[P]. 2006-1-3.
[6]张衍儒, 肖练刚,张继生,等. 旋转控制固定鸭舵的导航初始化与控制算法研究[J]. 航天控制,2014,32(6):34-39.
ZHANG Yanru, XIAO Liangang,ZHANG Jisheng,et al. Navigaion initialization and control algorithm of roll control fixed canards[J]. Aerospace Control, 2014,32(6):34-39. (in Chinese)
Research on Guidance Control Algorithm of Dual-spin Projectile with Fixed Canards
ZHANG Yanru1, XIAO Liangang1,ZHOU Hua1,CAO Ying2
(1.Beijing Aerospace Automatic Control Institute, Beijing 100854 China; 2.Chinese People’s Liberation Army 456th Hospital, Jinan 250031, Shandong, China)
According to the parabolic flight characteristics of the dual-spin projectile, a guidance algorithm was proposed for the purpose of reducing the cost and volume of guided weapon from the perspective of controlling the direction of the control force vector of the fixed canards based on GPS receiver andxaxis gyroscope. With no need for precise attitude information, the current attitude information in the proposed guidance method was computed by GPS receiver with flight stability realized by the static stability of the body, resulting in a correction of point difference. Finally, the applicability of the gui-dance control algorithm was analyzed and verified through an analysis of the error range of the attitude acquisition algorithm.
automatic control technology; fixed canards; dual-spin projectile; guidance control; attitude information collection
10.19323/j.issn.1673-6524.2016.03.005
2015-10-12
张衍儒(1985—),男,工程师,博士,主要战术武器系统综合技术研究。E-mail:457133417@qq.ccom
TJ412.+1
A
1673-6524(2016)03-0020-05
