一种适用于低成本制导火箭弹的坐标转换方法

刘 芳，王斌翊，何 浩，范 继，徐建锋

( 西北机电工程研究所，陕西 咸阳 712099)



一种适用于低成本制导火箭弹的坐标转换方法

刘 芳，王斌翊，何 浩，范 继，徐建锋

( 西北机电工程研究所，陕西 咸阳 712099)

基于某低成本制导火箭弹工程的研制背景，研究了制导火箭弹在飞行过程中不同坐标系间的转换关系。为了消除转换过程中的精度损失，深入分析了转换误差产生的原因；考虑弹载制导控制系统的实时处理能力，提出了一种适用于低成本制导火箭弹的坐标转换方法，并成功应用到数值仿真中。仿真结果表明：该方法能很好地兼顾误差和运算负荷，适于制导火箭弹的工程应用。

兵器科学与技术；制导火箭弹；坐标转换；误差分析；工程应用

常规武器成本低，但精度差；精确制导武器虽然命中精度高，但造价昂贵，生产和维护技术复杂，装备数量有限。低成本制导火箭弹是一种对点目标具有较高命中率的低成本灵巧弹药，能够以较低的成本显著提高现有武器系统的作战效能，具有较高的作战效费比。仅通过在常规火箭弹上加装GPS/INS组合导航系统及简单的控制组件，即可实现火箭弹的制导功能。由于GPS/INS组合导航系统提供的是WGS-84坐标系下弹体的位置与速度信息，而火箭弹的制导系统需要在发射坐标系下完成制导控制，为实施导航和控制，必须实时将GPS接收机给出的WGS-84坐标信息转换到发射坐标系，供给导航系统应用。

文献[1]在假设地球为圆球模型的前提下，提出了一种含有修正参数的坐标转换简化算法，并通过半实物仿真试验验证了模型的可行性；文献[2]提出了一种由GPS坐标系到当地水平游移坐标系的转换方法，并由跑车试验验证了偏航角理论值为0°时由惯性仪表测量数据和GPS数据解算出的偏航角基本一致；文献[3-5]分析了坐标转换过程中3个方面产生的误差，并阐述了相应的修正方案，对提高机载简易制导炸弹的命中精度起到了一定的作用。但上述文献在转换过程中均需要先转换至导航坐标系，再转换至发射坐标系。在弹体飞行过程中，必须实时计算导航坐标值，对于低成本制导火箭弹的简单控制组件而言，计算过于复杂。

笔者提出的坐标转换方法仅仅根据WGS-84坐标系和发射坐标系两者存在的固有转换关系，完成了坐标系间的一次转换，并通过引入准发射坐标系，在弹道轨迹开始和结束的关键时刻有效地消除了误差，提高了坐标转换精度，更适于低成本制导火箭弹的工程应用。

1 转换过程中涉及到的坐标系

1.1 WGS-84坐标系(Ow-xwywzw)

WGS-84坐标系是一个地球惯性坐标系，该坐标系有两种表达形式，即地心直角坐标系和大地坐标系。如图1所示，地心直角坐标系的原点Ow与地球质心重合，Owzw轴指向国际协议地球极方向，Owxw轴指向格林尼治本初(起始)子午面(即BIH国际时间局定议的起始子午面)和赤道的交点，Owyw轴与Owzw、Owxw轴构成右手直角坐标系。大地坐标则用纬度B、经度L和大地高h表示。GPS接收机输出的就是基于WGS-84大地坐标系的信息。

1.2 导航坐标系(On-xnynzn)

导航坐标系,也称地理坐标系,如图2所示，是以弹体的质心On为原点，Onxn轴沿参考椭球卯酉圈方向指向东，Onyn轴指向北，Onzn轴则与Onxn、Onyn轴构成右手直角坐标系。坐标值随着弹体的移动不断变化。

1.3 发射坐标系(Of-xfyfzf)

发射坐标系，也称地面坐标系，如图3所示，它主要用来描述弹体质心相对于发射点的运动，在弹体发射瞬间建立。以发射点到地面的投影Of为原点，Ofxf轴在Of点椭球面的切平面内指向目标点方向，Ofyf轴与Of点椭球面的法线重合，指向朝上，Ofzf轴则按右手坐标系确立。

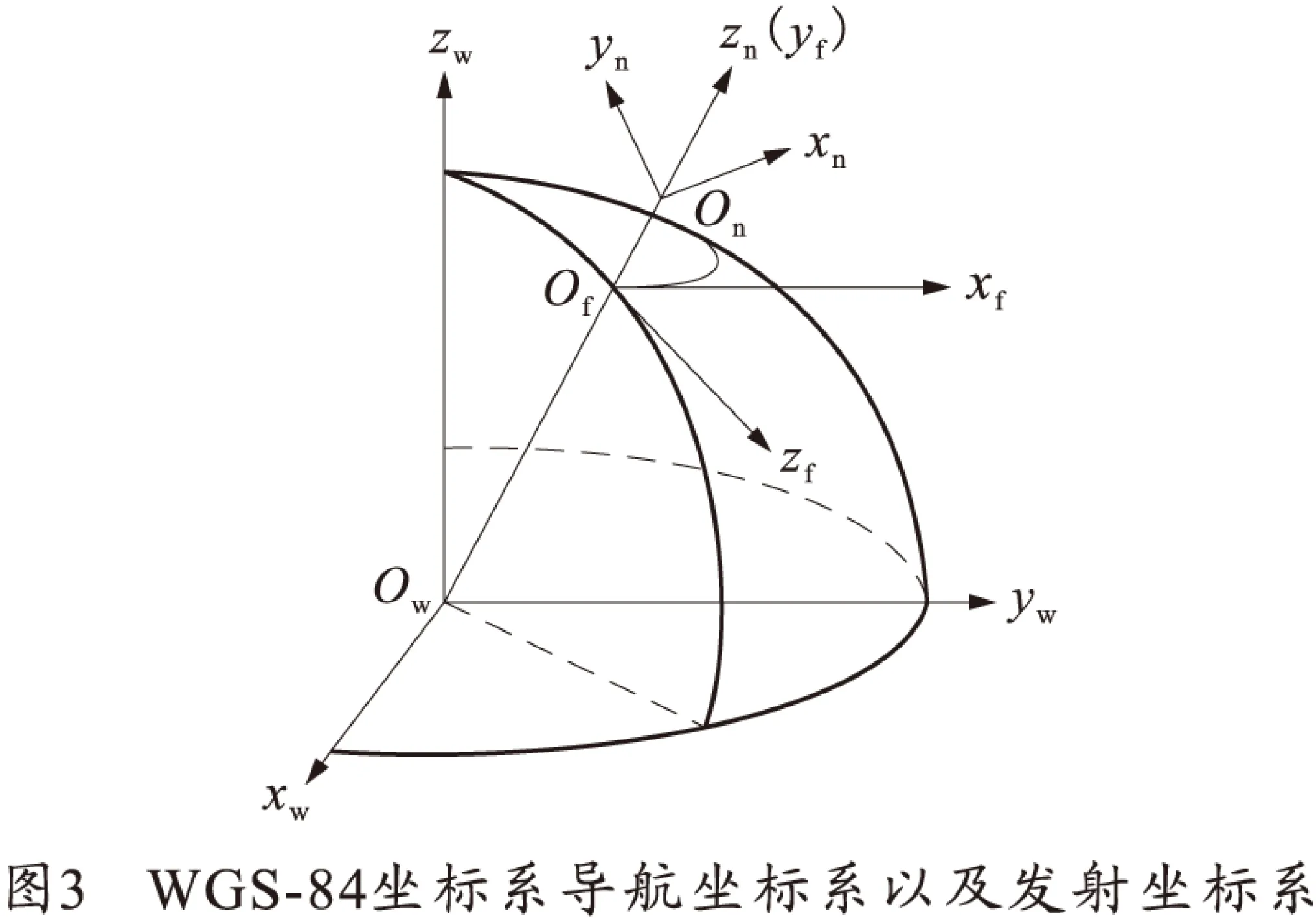
2 坐标转换

弹体飞行时坐标转换的过程为通过发射点L、目标点T以及弹体质点在空中任意时刻位置Fn的GPS信息，最终获取Fn在发射坐标系下的位置信息，经以下2个步骤即可完成。

2.1 WGS-84大地坐标系到WGS-84地心直角坐标系的转换

弹载GPS接收机输出的是基于WGS-84大地坐标系的信息。在已知地球空间某点P的WGS-84大地坐标[BPLPhP]T，由式(1)可以获得该点的WGS-84地心直角坐标[6]：

(1)

2.2 WGS-84地心直角坐标系到发射坐标系的转换

发射坐标系也是一个惯性坐标系，与WGS-84地心直角坐标系仅存在固有的转换关系，通过3次旋转和1次平移便可实现。其步骤如下：先将WGS-84地心直角坐标系绕z轴旋转-(90°-LL)，再绕x轴旋转BL，接着围绕y轴旋转-(90°+ψA)，最后将原点由Ow平移至Of。其中，LL、BL分别是发射点L在WGS-84大地坐标下的经度和纬度；ψA是发射平面与北向的夹角[1]，随发射坐标系确立而固化，由地面发射控制系统给出。旋转矩阵的计算[7]为

(2)

式中：

3 发射坐标系建立时产生的误差

3.1 误差分析

由发射坐标系的定义可知发射坐标系的原点是发射点L在地面的投影Of，Ofxf轴在Of点椭球面的切平面内指向目标点T方向，如图4所示。

假设发射坐标系建立瞬间，发射点L和目标点T的GPS信息已知且都在椭球面上,那么实际地面的目标点T并不是由发射坐标系得到的目标点T′，这就产生了水平方向误差Δx和高度方向误差Δh。

3.2 该误差对坐标转换的影响及修正方法

由3.1分析可知，发射坐标系建立时产生的误差将会随射程增大而增加，具体影响如表1所示。

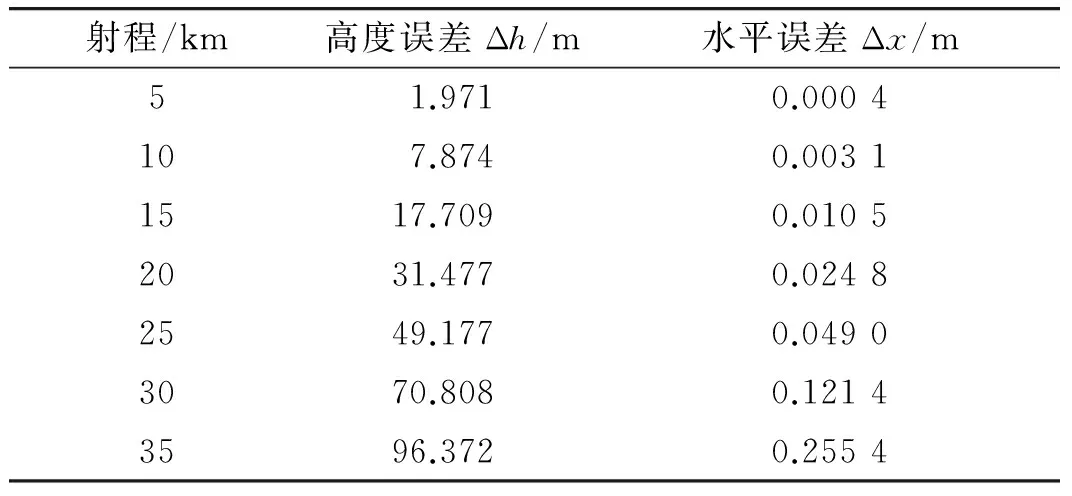
表1 高度和水平方向误差随射程的变化

由表1可以看出，在射程变化范围内水平误差相对很小，高度误差则很大，当射程超过10 km，高度误差难以忽略。而本文的研究背景射程都在30 km以上。因此，在弹体飞行过程中需要对误差进行实时修正。一般的修正方法：一是推导公式，即通过存储在弹载计算机中的公式来实时计算误差量，从而进行补偿；二是查表法，将射程内的误差尽可能精细的列出并存储在弹载计算机上，通过查表补偿。

文献[1]提出的是一种基于迭代的坐标转换方法,由于没有考虑误差的因素，将给系统带来不断增大的误差积累。文献[5]则在此基础上提出了一种基于目标点跟踪的坐标转换方法，并分析了误差的来源和修正方法，虽然随着弹体不断接近目标，误差能够收敛，但就试验结果看，研究者并未对所分析的误差进行直接处理，仅仅是将该误差转移到了炸弹的投射时刻，对于水平射程为10 km以内的机载炸弹而言，这样做是简便有意义的，但就本文的研究背景来说，这种初始误差会对弹体造成致命的影响。笔者提出的坐标转换方法将引入准发射坐标系这一概念，并在该坐标系下完成飞行数据比较，该方法能够在弹道轨迹开始和结尾的关键时刻有效地消除发射坐标系建立产生的误差。

4 基于准发射坐标系的坐标转换

在发射平面内，以发射点L为原点，发射点L指向并经过弹着点T的方向为x轴，取过发射点L的铅垂线作为y轴，使z轴过发射点且垂直于发射平面，建立准发射坐标系L-xf′yf′zf′， 如图5所示。

由3.1所述，假设条件是发射点L和弹着点T都在椭球面上，更普遍的情况则是发射点L和弹着点T均不在椭球面上。根据准发射坐标系的定义可知：准发射坐标系与发射坐标系存在固有的旋转和平移关系，其旋转矩阵为

(3)

式中：α是发射坐标系围绕z轴旋转形成准发射坐标系时所旋转的角度，且α=arctan[(yTf-hL)/xTf]，[xTfyTy0]T是弹着点T在发射坐标系下的坐标值，hL是发射点L的GPS大地高。

4.2 基于准发射坐标系的坐标转换

引入准发射坐标系后，坐标转换是为获取准发射坐标系下Fn的位置坐标。

已知发射点L、目标点T以及弹体质点在空中任意时刻位置Fn在WGS-84大地坐标系下的坐标分别为[BLLLhL]T、[BTLThT]T、[BFnLFnhFn]T，且发射点与目标连线与北向的夹角ψA已知，将弹体的坐标信息由大地坐标系转换成准发射坐标系的流程如下：

1)根据式(1)计算出L、T和Fn点在WGS-84地心直角坐标系下的坐标[xLwyLwzLw]T、[xTwyTwzTw]T、[xFnwyFnwzFnw]T。

2)由式(2)的旋转矩阵计算出弹着点T在发射坐标系下的坐标值[xTfyTf0]T。

3)根据式(3)计算α。

4)由式(4) 计算出弹体在准发射坐标系下的坐标[xFnf′yFnf′zFnf′]T。

(4)

5)在准发射坐标系下设计制导火箭弹理论弹道数据，用于指导弹体质点的飞行。

5 仿真试验及结果分析

根据上述方法进行了数值仿真，图6为仿真试验的数据流程图。

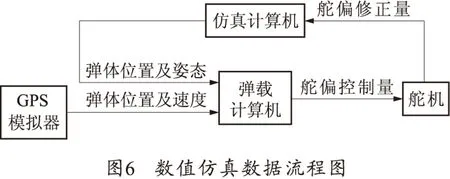
试验过程中，采用GPS模拟器模拟制导火箭弹在空中飞行时的GPS定位信息，发送给弹载计算机进行坐标转换，并进行制导控制。将坐标转换后的弹道信息与理论弹道进行比较，就能看出坐标转换的误差。试验的发射点L、目标点T的GPS坐标已知，射程约35km。

图7和图8分别为未采用处理误差的方法和采用本文方法对转换前后弹道坐标进行了比较。其中，图7(a)、 图8(a)均包含2条曲线，却因为误差相对整个弹道太小而看似重合；为了能够清楚地了解坐标转换的误差，图7(b)和图8(b)表示了两种方法坐标转换的误差曲线；同时为了更进一步表明弹道末端的误差收敛情况，图7(c)和图8(c)对弹道末端区域进行了放大处理。

可以看出，对于试验的35km射程，未处理误差的坐标转换方法会在弹道轨迹的尾部造成约100m的高度差距，这通过误差曲线也可以看出来；而本文所述的坐标转换方法不但能够减小这种因为发射坐标系建立而带来的误差，而且在弹道轨迹开始和结束的关键时刻使误差收敛至0，很好地完成了坐标转换目的，为实现低成本指导火箭弹的精确制导提供了有力条件。

6 结论

经过以上的数值仿真，可以看出笔者提出的坐标转换方法的理论模型计算结果精度较好，其理论模型的假设条件可行，修正措施合理，能够很好地减小因发射坐标系建立带来的误差，并且在弹道轨迹开始和结束的关键时刻使误差收敛至0，从而为高精度制导提供了有力条件。

References)

[1]刘敏．坐标转换在组合导航系统半实物仿真中的应用

[J]．计算机仿真，2005，22(10)：136-139．

LIU Min. Application of coordinate transformations in the hard-ware in-the-lop simulation of integrated navigation system[J]. Computer Simulation, 2005,22(10): 136-139. (in Chinese)

[2]孔祥雷，李杰，杜英．MEMS-IMU/GPS组合导航系统中坐标系统一的方法研究[J]．传感技术学报，2010,23(4)：522-524．

KONG Xianglei, LI Jie, DU Ying. Method of coordinate system unity in MEMS-IMU /GPS integrated navigation system[J]. Chinese Journal of Sensors and Actuators, 2010, 23(4):522-524. (in Chinese)

[3]胡锐，薛晓中，孙瑞胜，等．制导炸弹中坐标转换的误差分析及修正[J]．弹道学报，2008，20(4)：36-40.

HU Rui, XUE Xiaozhong, SUN Ruisheng, et al. Error analysis and modifying method of coordinate transformations in guided bomb[J]. Journal of Ballistics, 2008, 20(4): 36-40. (in Chinese)

[4]吴盘龙，姜福先．精确制导炸弹坐标转换技术[J]．中国惯性技术学报,2008,16(2)：174-177.

WU Panlong，JIANG Fuxian. Technology of coordinate transform for precision-guided bomb[J]. Journal of Chinese Inertial Technology, 2008,16(2)：174-177. (in Chinese)

[5]吴盘龙，薄煜明，胡瑞．简易制导炸弹坐标转换的误差分析与修正[J]．兵工学报，2008，29(10)：1272-1276.

WU Panlong, BO Yuming, HU Rui. Error analysis and modification of coordinate transform of simplified guided bomb[J]. Acta Armamentarii, 2008，29(10)：1272-1276. (in Chinese)

[6]袁建平，方群，郑谔．GPS在飞行器定位导航中的应用[M]．西安：西北工业大学出版社，2000：4-25．

YUAN Jianping，FANG Qun, ZHENG E. Application of GPS navigation in aircraft positioning[M]. Xi’an: Northwestern Polytechnical University Press，2000：4-25．(in Chinese)

[7]秦永元．惯性导航[M]．北京：科学出版社,2006:5-8.

QIN Yongyuan. Inertial navigation[M]. Beijing: Science Press, 2006:5-8. (in Chinese)

A Method of Coordinate Transformation for Low-cost Guided Rocket Projectiles

LIU Fang, WANG Binyi, HE Hao, FAN Ji, XU Jianfeng

(Northwest Institute of Mechanical and Electrical Engineering, Xianyang 712099, Shaanxi, China)

Based on the engineering background of the low-cost guided rocket projectiles, the transformation relations between different coordinate systems of the guided rocket projectiles in flight were investigated. It is considered that the precision loss of the coordinate transformation should be strictly handled for good messages in navigation. An analysis was made of the reason of errors on precision. Meanwhile, a new simple method of coordinate transformation was provided for easing real-time processing pressure of missile-borne computer, which is successfully applied in semi-physical simulation. The simulation result shows the correctness and feasibility of the method in engineering application of guided rocket projectiles, for it takes into account both precision loss and calculations.

ordnance science and technology；guided rocket projectiles; coordinate transformation; error analysis; engineering application

10.19323/j.issn.1673-6524.2016.03.008

2015-04-29

刘芳(1984— )，女，硕士，工程师，主要从事火炮、自动武器与弹药工程技术研究。E-mail：vivian519cute@163.com

TJ012

A

1673-6524(2016)03-0036-05