课堂为媒 旧知引路——浅谈迁移法在小学数学教学中的应用

浙江省义乌市青口小学　贾建萍

课堂为媒旧知引路——浅谈迁移法在小学数学教学中的应用

浙江省义乌市青口小学贾建萍

我们总会看到各种各样的迁移现象，比如在语言的学习上，通常英语好的人学习起法文来也是得心应手；再比如如果一个人会开大货车，那么他开起小轿车来也很简单；又或者学生在学好了乘法之后学习除法就很简单了。此外，也可以看到一些与此相反的现象，如一些外国人在学习汉语的时候，会觉得拼音很难学，时常与英文字母混淆；人们通常会把工作中的坏情绪带入私人生活中。类似上面所说的现象，都是迁移现象。

我们知道学习是一个连续的过程。在学习的过程中，学习者学习新知识的多少、掌握新知识的速度都取决于他们已有的知识系统、对新知识的渴望程度，反过来，学习新知识的过程也将影响到已有的知识系统及学习新知识的方法，这就是学习过程中的迁移现象。换句话说，这种在新知识的学习过程中已有知识与新知识的相互影响就是学习过程中的迁移。需要提出的是，将自己学到的知识应用到实际问题的解决中也是学习过程中的迁移。

为了帮助学生更轻松地学好课堂知识，我们可以研究这种迁移规律，将其应用到课堂中。结合个人经验，我将对这个操作步骤分四点进行阐述。

一、夯实基础，创设条件

迁移是已有知识与新知识的相互影响，从这方面来看，我们需要帮助学生夯实基础。就像盖一座高楼，地基是根本，而基础就是盖知识大楼的根本。学生的知识系统越扎实，才能更容易依靠迁移规律学习到更多新知识，大楼才能盖得更高。

举例来说，我在给学生们讲解周长相关的课程时，先采用手势教学的方法，让学生们理解了周长是指物体表面或图形一周的长度，长方形周长为长与宽之和的两倍，再进行讨论，得出周长的数学表达式为长的两倍加宽的两倍或为长与宽的和乘二。紧接着出示一组练习巩固课堂教学，问“：将一个边长为7米的正方形相框改为一个长为8米的长方形相框，则该长方形相框的宽为几米？”学生出现了多种解法：①（7×4-8×2）÷2=6（厘米）②7×2-8=6（厘米）③7-（8-7）=6（厘米）……由上述的后两种解题方法我们可以知道，当面对周长问题时，学生们的脑海里就出现了“周长是长与宽的和乘二”这个具体的思维表象。可以看出，夯实基础是快速学习新知识、保证迁移规律更好发挥作用的根本保证。

二、揭示联系，促进迁移

迁移的前提是要让学生先学会概括，概括是迁移的核心，它能使学生把一般的原理和概念运用到其他的学习情境中，而不必对每一个特殊的学习情境做出新的反应。因此，作为教师要先学会揭示新旧知识间的联系，而揭示联系的方法有很多，如通过比较、分类、抽象、归纳等，这样就能将所教知识进行概括，并且形成一种概括的习惯，发展学生的迁移能力。

例如，在教学“除数是小数的除法”这节课时，我们可以从小数点如何处理入手来设计一组练习，有了这组习题的铺垫，就能更好地引导学生把“除数是小数的除法”转化为“除数是整数的除法”。（1）在一个除法算式中，如果除数扩大10倍，要使商不变，被除数应该怎样？除数扩大100倍呢？（2）把3.56扩大10倍，小数点应该怎样移动？扩大100倍呢？在课后作业中，我们还可以设计这样一组练习：在（）里填上适当的数。

这是一组针对性练习，本组题只要求将“除数是小数的除法”转化为“除数是整数的除法”，不必再去计算，它的目的就在于训练学生小数点的处理能力。这样既抓住了本课的重点，又给了学生充分的时间去突破难点，有利于知识的迁移。

心理学家B.S.布卢姆认为，前面的学习要达到80%～90%的正确率才能开始新的学习。由此可见，教师在教学中应努力使学生巩固好之前学的知识，在此基础上再进入后面知识的探究和学习。实践证明，原有知识、技能越是熟练，迁移速度就越快，越有效。

三、分析比较，灵活迁移

比较是一种方法，通过比较我们能知道各种事物间的区别与联系，从而认识某种事物。比较是我们思维的基础。在小学数学教材中有很多内容既有联系又有区别。所以教学时，我们可以选择一些有代表性的内容，引导学生运用比较的方法，抓住知识间的联系点和分化点，灵活迁移，这样能使学生的理解和掌握达到更深的境界。

例如，教学正方形面积计算公式，我是这样设计的：（一）探究长方形面积的计算方法。1.课件出示几个不同的长方形。2.四人小组合作，每组选一个长方形进行研究。3.汇报交流方法。4.小结。（二）探究正方形面积的计算方法。1.量出手中正方形的边长，比较一下长方形与正方形，看看有什么关系。2.交流总结：正方形是长、宽相等的特殊的长方形。3.猜想一下正方形的面积应该怎样计算。4.生：因为正方形是长、宽相等的特殊的长方形，所以：正方形的面积=边长×边长。

以上设计先通过学生自己动手实践、合作探究，总结出长方形面积的计算方法，再引发学生思考、讨论，在学生掌握了长方形面积计算的基础上，大胆猜想正方形的面积计算方法，激发学生学习数学的兴趣，诱发其内在的学习动机，促使学生积极、主动、创造性地思维，同时也培养了学生迁移类推的能力。

四、重视变式，巧用迁移

迁移理论认为，学生对一般规律和概括性知识的掌握是通过最初学习时运用各种变式达到的，同时又认为，只有学生认识到一个规律可运用于各种不同的学习情境，并形成在各种不同的学习情境中运用这些规律和知识的定势时，这些规律和知识才算真正被掌握而具有显示价值。因此，在教学中要达到灵活运用知识的目的，实现有效迁移，变式就显得更加重要。

例如，在教学北师大版三上“里程表”一课时，我先设计了这样的前置作业：

在书本的整理与复习中也有这样的练习（见文末图）：

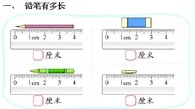
除了以上的两道习题外，像用一根“断尺”来测量物体的长度，家里的电表、水表读数等一些问题，都是很有针对性的一些变式。

教学实践证明，迁移教学能有效地落实课堂素质教育，它注重“四基”的落实（“四基”只有达到一定的程度，才能有效实施迁移）、能力的培养（特别是观察、比较、分析、动手操作、综合概括能力）以及注意联系生活实际培养学生开放性、创新性思维，有利于提高课堂教学效率，减轻学生负担，全面提高学生的综合素质。

迁移是数学学习中的一种普遍现象。正是由于迁移，学生掌握的数学知识才能以某种方式联系起来，并能够在解决数学问题的过程中发挥作用。数学新知识的掌握总在某种程度上改变着已有的数学认知结构，学生对已经掌握的不同数学知识进行组合，往往可以形成新的数学知识。诸如此类的数学知识之间的相互影响，都是数学学习的迁移现象。