损失规避环境下集装箱班轮舱位超售决策研究

顾波军龙莹

（1.浙江海洋大学经济与管理学院，浙江舟山316022；2.浙江海洋大学海运与港航建筑工程学院，浙江舟山316022）

损失规避环境下集装箱班轮舱位超售决策研究

顾波军1龙莹2

（1.浙江海洋大学经济与管理学院，浙江舟山316022；2.浙江海洋大学海运与港航建筑工程学院，浙江舟山316022）

超售策略是集装箱班轮运输的常用策略，有利于提高舱位资源的利用效率，进而提高班轮运输效益。基于心理账户理论，本文首先构建了损失规避环境下集装箱班轮超售决策模型，并揭示了单位超售成本、单位舱位成本以及损失规避对于最优超售水平的影响机制；其次，本文采用数值算例研究方法，对损失规避环境下基于多重心理账户的超售决策模型与基于单一心理账户的超售决策模型进行了比较研究，研究结果表明，按照多重心理账户超售决策模型，集装箱班轮运输企业的超售水平更低、期望收益更高。本文的研究结论对于优化集装箱班轮舱位超售决策具有重要意义。

损失规避；心理账户；超售决策

一、前言

超售策略最早在航空客运中得到应用，并大幅改善了航空公司收益，相关的研究已有很多，例如Beckmann［1］、Shlifer和Vardi［2］、Belobabap［3］、Rothstein［4］、Subramanian等［5］、Kasilingam［6-7］。超售策略对于集装箱运输同样具有重要意义，是集装箱班轮运输的常用策略，即预先销售比实际舱位更多数量的舱位，从而弥补起航时因预订舱位未履约而使舱位闲置所引起的机会收入损失。相比于航空运输，关于集装箱运输超售问题的研究相对较少。如李冰州等基于期望成本最小研究了能力随机的海运集装箱舱位超售问题。［8］阳成虎等采用CVaR准则研究了风险规避情境中的集装箱舱位超售决策，并分析了风险规避对超订决策的影响机制。［9］

自从Kahneman和Tversky［10］提出前景理论以来，决策者损失规避的特征得到了广泛的验证。Schweitze和Cachon［11］最早将损失规避行为引入经典报童模型，Wang和Webster［12］等则将其拓展到考略缺货损失的报童模型，并发现缺货损失较高时，损失规避报童的订货量比风险中性报童的订货量更高。此后的学者进一步从超售心理成本厌恶程度大于失售心理成本［13］、竞争型报童［12］等方面对损失规避报童的订购决策进行了研究。但上述文献基于损失规避价值函数的研究均假设决策者面临的是基础收益，价值函数评价的也是单一心理账户。但报童问题的收益属于复合收益，例如当市场需求小于订购量时，报童的复合收益就包括销售收益和超售损失，且属于不同的类型，于是，决策者将形成多重心理账户［14-16］，例如销售收益账户和超售损失账户。Ho和Zhang［17］、Becker-Peth等［18］、顾波军和张祥［19］等学者率先将多重心理账户用于报童问题与供应链契约协同研究，使得理论模型的研究具有了更好的解析特征。

基于多重心理账户，本文构建了集装箱班轮超售决策的损失规避报童模型，分析了班轮运输企业的最优超售水平；并与损失规避环境下基于单一心理账户的超售决策模型进行了比较研究，研究表明，基于多重心理账户的超售决策模型能够使班轮运输企业获得更高的期望收益。

二、模型构建

（一）问题描述与假设条件

考虑集装箱班轮运输企业的超售决策，假设班轮舱位容量为C，单位舱位成本为w，单位舱位超售惩罚为v，单位舱位出售价格为p。班轮运输企业制定的超售水平为Co，假设履约率x是一随机变量，并假设x（0≤x≤1）具有概率密度函数与累积分布函数f（x）和F（x），且假设F（x）是连续、可导且可逆。当履约率较高时，超售决策会造成超售成本，即x>C/Co时，超售惩罚为v（xCo-C）；而当履约率较低时，舱位闲置会产生机会成本，即x≤C/Co时，舱位闲置成本为w（C-xCo）。因此，超售策略的决策者面临经典的报童问题。本文进一步假设超售决策者是损失规避的，并定义损失规避效用（价值）函数［11］为：

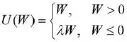
其中，λ为损失规避系数，且λ>1。

（二）损失规避环境下基于多重心理账户的超售模型

班轮运输企业实施超售策略，并记CoM为基于多重心理账户超售模型制定的超售水平。当履约率较低时，班轮运输企业的收益为舱位销售收益（p-w）CoMx和舱位闲置成本w（C-CoMx）的差；履约率较高时，班轮运输企业的收益为舱位销售收益（p-w）C和超售惩罚v（CoMx-C）的差。因此，损失规避班轮运输企业的决策者将形成多重心理账户，在履约率较低时，形成舱位销售收益账户和舱位闲置成本账户；在履约率较高时，形成舱位销售收益账户和超售惩罚账户。当决策者具有多重心理账户时，价值函数将分别进行评价。因此，基于多重心理账户的损失规避超售决策者的期望效用EUπLM为：

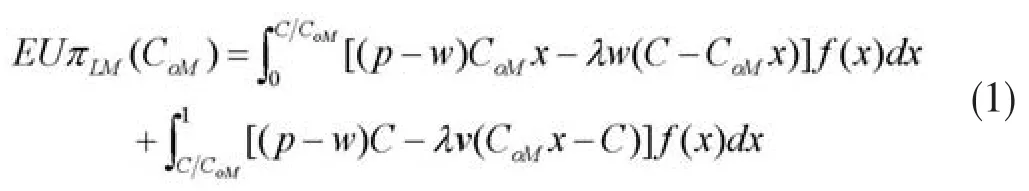
性质1：期望效用EUπLM（CoM）是关于CoM的凹函数，在定义域（0，∞）存在唯一最优解使得EUπLM（CoM）取得最大值，且CoM*满足：

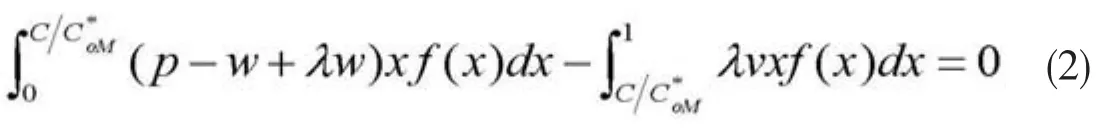
性质1证明：

对式（1）求一阶导数和二阶导数，可得：

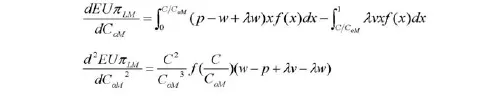
因为，CoMmin=C、CoMmix=∞，可得：

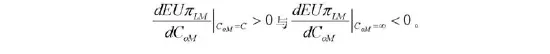
因此，在定义域（0，∞），EUπLM有唯一最优值CoM*，且满足式（2）。

证毕。

性质2：基于多重心理账户，损失规避班轮运输企业制订的超售水平随单位舱位成本w的增大而增大，随单位舱位超售成本v的增大而减小。

性质2证明：

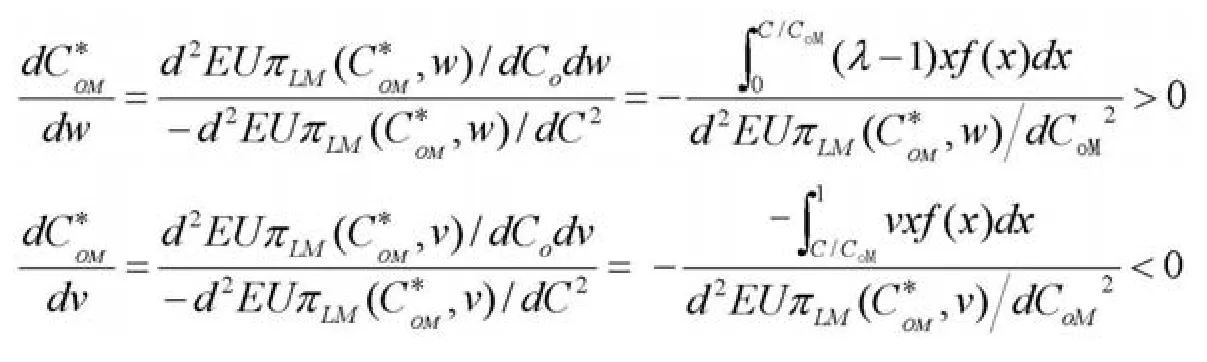
证毕。

由性质1可知，基于多重心理账户，损失规避超售决策者在制订超售水平时存在唯一最优解。性质2表明，超售决策者在制订超售水平时是以期望效用最大化为基准的，所以当单位舱位成本增加时，班轮运输企业将会制订更高的超售水平，以确保舱位使用率，从而减少由于舱位闲置而带来的损失；当单位超售成本增加时，超售决策者将会减少超售水平，从而降低由舱位超售带来的损失。

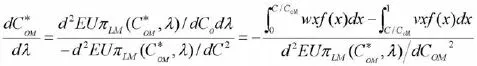
观察1：基于多重心理账户，损失规避班轮运输企业制订的超售水平随损失规避系数λ的增大而减小。

令C=10000，p=1000，w=600，v=300，λ∈［1，3］，且步长为0.1，假设x服从均匀分布，即f（x）=1，通过Matlab2013进行数值算例分析，可得图1。由图1可知，当履约率x服从均匀分布时，在给定参数设置下，CoM*随着损失规避程度的增加而减少，即超售决策者越损失规避，则会制订越低的超售水平，减少由舱位超售带来的损失，从而获得较高收益。

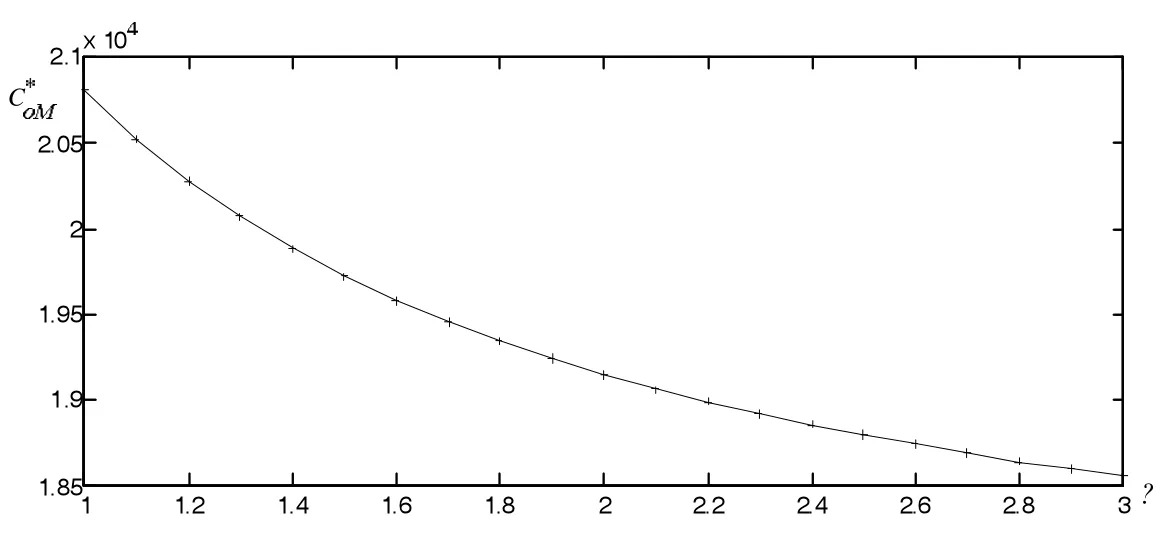
图1　CoM*随损失规避程度变化关系

记CoS为基于单一心理账户超售模型制定的超售水平，并记EUπLS（CoS）为基于单一心理账户超售模型下的期望效用，可得：

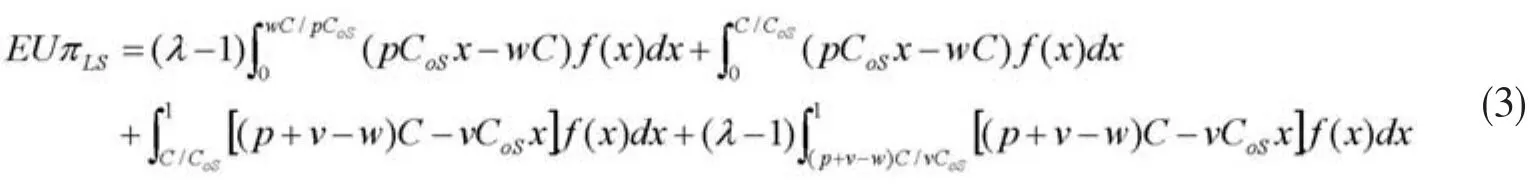
引理1：期望效用EUπLS（CoS）是CoS关于的凹函数，在定义域（0，∞）存在唯一最优解使得EUπLS（CoS）取得最大值，且满足：

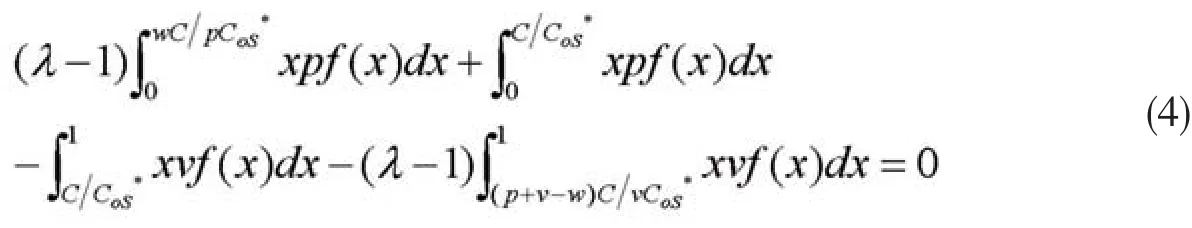
引理1证明：

分别对式（3）求一阶导数和二阶导数，可得：

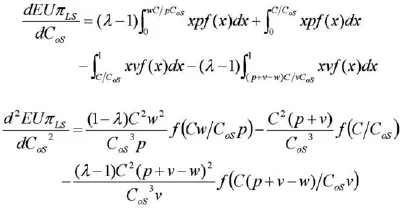
因为Comin=C、Comix=∞以及，可得：

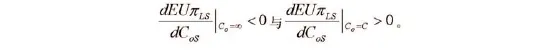
因此，在定义域（0，∞），EUπLS有唯一最优值，且满足式（4）。

引理1说明，在损失规避环境下，班轮运输企业基于单一心理账户下制定超售水平时存在最优解，即在这种情形下，当班轮运输企业的超售水平为CoS*时，班轮运输企业的期望效用最大。

观察2：损失规避环境下，基于多重心理账户超售决策模型制定的超售水平小于基于单一心理账户超售决策模型制定的超售水平CoM*＜CoS*，即；集装箱班轮运输企业基于多重心理账户超售决策模型获得的期望收益大于基于单一心理账户超售决策模型获得的期望收益，即EUπLS（CoM*）＜EUπLS（CoS*）。

同观察1的参数设置，并按照式（2）和式（4）运用Matlab2013分别计算最优超售水平CoM*与CoS*，进而计算期望收益EUπLS（CoM*）与EUπLS（CoS*），如表1所示。

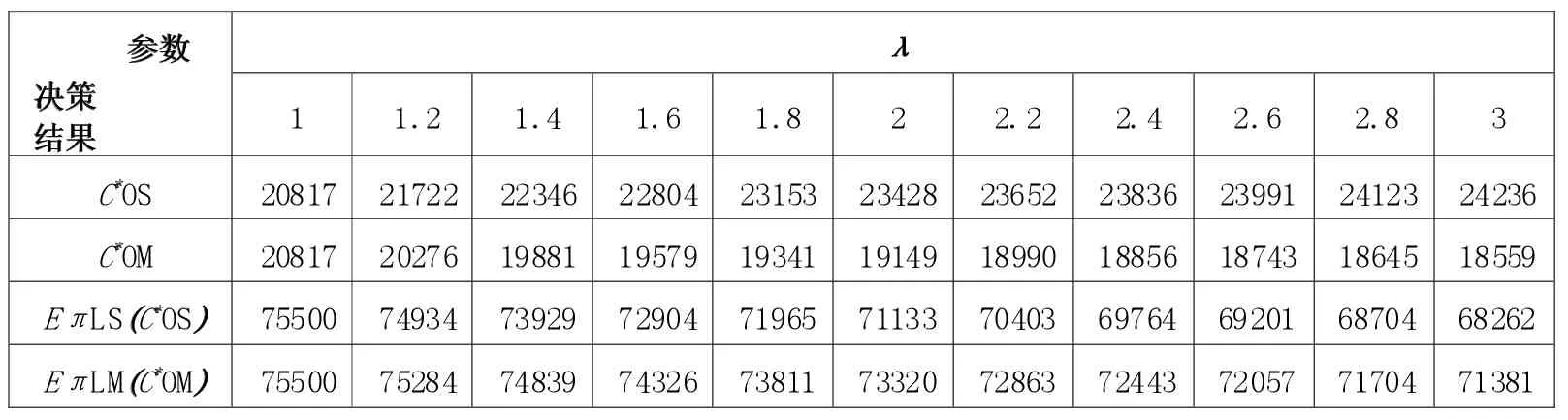
表1　基于多重心理账户的超售决策与基于单一心理账户的超售决策比较

观察2表明，相比于单一心理账户决策模型，采用多重心理账户决策模型可降低班轮运输企业的超售水平，并能获得更高的收益。以表1为例，当λ=2时，班轮运输企业的超售水平降低了18.26%，期望收益增加了1.9%。因此，采用多重心理账户决策模型，不仅可以降低班轮运输企业的超售风险，并且能够通过优化决策提高收益。

三、结论

随着集装箱船舶的大型化，超售策略是使其实现管理现代化的重要管理工具，不仅可以充分利用有限的舱位资源，而且可以使自身收益最大化。首先，本文基于多重心理账户构建了损失规避环境下班轮运输超售决策模型，证明班轮运输超售决策存在唯一最优解；并通过敏感性分析揭示了单位超售成本、单位舱位成本对最优超售水平的影响机制，即最优超售水平随着单位超售成本的增大而减小、随着单位舱位成本的增加而增大；数值算例研究进一步显示最优超售水平关于损失规避单调递减。其次，采用数值算例研究方法，本文对损失规避环境下基于多重心理账户的超售决策与基于单一心理账户的超售决策进行了比较研究，研究结果显示，按照多重心理账户超售决策模型，班轮运输企业的超售水平更低、期望收益更高。因此，本文的研究改善了损失规避环境下班轮运输超售决策，能够为班轮运输企业的超售决策提供一种更为优化和合理的决策方法，对损失规避环境下的班轮运输企业制订超售水平具有重要意义。

［1］Beckmann S L.Decision and team problems in airline reservation［J］.Econometrica，1958（26）：134-135.

［2］Shlifer R，Vardi Y.An airline overbooking policy［J］.Transportation Science，1975（9）：101-114.

［3］Belobabap P P.Air travel demand and airline seat inventory management［D］.Cambridge：Flight Transportation Laboratory，Massachusetts Institute of Technology，1987.

［4］Rothstein M.An airline overbooking model［J］.Transportation Science，1971（5）：180-192.

［5］Subramanian B J，Stidham S，Lautenbacher C J.Airline yield management with overbooking，cancellations，and no-shows［J］. Transportation Science，1999，33（2）：147-167.

［6］Kasilingam R G.Air cargo revenue management：characteristics and complexities［J］.European Journal of Operational Research，1996，96（1）：36-44.

［7］Kasilingam R G.An economic model for air cargo overbooking under stochastic capacity［J］.Computers Industry Engineering，1997，32（1）：221-226.

［8］李冰州，武振业.能力随机的海运集装箱收益管理超订模型［J］.西南交通大学学报，2006，41（4）：501-506.

［9］阳成虎，杜文等.基于CVaR的海运集装箱超订模型［J］.西南交通大学学报，2007，42（5）：636-640.

［10］Kahneman D，Tversky A.Prospect theory：An analysis of decisions under risk［J］.Economertrica，1979，47（2）：263-291.

［11］Schweitzer M E，Cachon G P.Decision bias in the newsvendor problem with a known demand distribution：Experimental evidence［J］. Management Science，2000，46（3）：404-420.

［12］Wang C X，Webster S.The loss-averse newsvendor problem［J］.Omega，2009，37（1）：93-105.

［13］Ho T，Lim N，Cui T H.Reference dependence in multi-location newsvendor models：a structural analysis［J］.Management Science，2010，56（11）：1891-1910.

［14］Kahneman D，Tversky A.The Framing of Decision and The Psychology of Choice［J］.Science，1981，211（1）：453-458.

［15］Thaler R.Mental Accounting and Consumer Choice［J］.Marketing Science，1985，4（3）：199-214.

［16］Thaler R.Mental Accounting Matters［J］.Journal of Behavioral Decision Making，1999，12（3）：183-206.

［17］Ho T，Zhang J.Designing Pricing Contracts for Boundedly Rational Customers：Does the Framing of the Fixed Fee Matter？［J］. Management Science，2008，54（4）：686-700.

［18］Becker-Peth M，Katok E，Thonemann U W.Designing Buyback Contracts for Irrational But Predictable Newsvendors［J］. Management Science，2013，59（8）：1800-1816.

［19］顾波军，张祥.风险中性供应商与损失规避零售商基于收益共享契约的供应链协调［J］.系统管理学报，2016，25（1）：67-74.

On Overbooking Decisions of Container Liners’Shipping Space under Loss-aversion Context

GU Bojun1LONG Ying2
（1.School of Economics and Management，Zhejiang Ocean University，Zhoushan 316022，China；2.School of Maritime and Civil Engineering，Zhejiang Ocean University，Zhoushan 316022，China）

Overbooking is a commonly used strategy to the container liners，helpful to improve the utilization efficiency of shipping space so as to enhance the benefit of the container liners.Firstly，an overbooking decision model is set up for container liners under loss-aversion context based on mental accounting theory，thus，revealing the mechanism of the unit overbooking cost，the unit shipping space cost and the loss-aversion to the optimal overbooking level.Secondly，a comparison is made between the overbooking decision model based on multi-mental accounting with the overbooking decision model based on single-mental accounting under loss-aversion context by numerical experiments，showing that the container liners have the lower level of overbooking and the higher level of expected revenue under overbooking decision model based on multi-mental accounting.Therefore，our research is of importance to optimize the container liners’overbooking decision.

loss-aversion；mental accounting；overbooking decision

F224

A

1008-8318（2016）04-0053-05

2016-06-12

浙江海洋大学“海洋科学”省重中之重学科开放课题。

顾波军（1980-），男，浙江岱山人，副教授，博士，研究方向：行为运作管理与供应链管理；龙莹（1991-），女，云南大