基于乘客选择行为的可召回机制优化模型
2018-10-17殷芳义肖梦婷YINFangyiLIChengXIAOMengting
殷芳义,李 程,肖梦婷 YIN Fangyi,LI Cheng,XIAO Mengting
(上海工程技术大学 航空运输学院,上海 201620)
(School of Air Transportation,Shanghai University of Engineering Science,Shanghai 201620,China)
0 引言
航空收益管理[1]是航空公司提高企业收益的重要技术,目前已成为决定国内外航空公司的盈利与亏损的手段。航空客运收益管理的核心内容是舱位控制,航空公司收益管理的舱位控制策略是指航空公司根据乘客的需求差异,将飞机可用座位划分为不同的等级(高价舱位和低价舱位)进行销售,以满足高价票乘客需求为基础,其关键的控制决策包括低价舱位与高价舱位的票数分配决策,将合适的座位分配给最合适的乘客,以此来获得企业最大的收益[2]。
需求预测是舱位控制的基础。由于乘客对航空公司的高等级舱位需求变化是具有随机性,这就导致对高等级舱位的需求预测是几乎难以确定。高舱位需求预测不准时存在如下两种可能的情形[3]:
(1)实际需求高于预测需求,即航空公司提供的舱位订座容量不能满足高舱位乘客。此时,航空公司一般采用超售的技术解决,但是超售会有可能导致拒绝登机(Denied Boarding)现象,航空公司因此要解决拒绝登机问题必然要增加额外的生产成本,并且严重地影响了航空公司的形象。
(2)实际需求低于预测需求,即航空公司提前确定的舱位订座容量供大于求。此时,没有预期的高舱位乘客前来购买高舱位,造成闲置损失(Spoilage)现象,也就是航空公司座位虚耗而收益损失。
为解决这两种情况而对航空公司造成的收益损失,Gallego(2004)提出了航空客运舱位柔性控制方法——可召回机制。这种制度要求在低价舱位中设置可召回票(Callable Tickets),并和普通机票同时出售,在高价舱位乘客需求超过剩余可用座位时召回已销售的可召回票。被召回的乘客可提前得到通知,并可得到补偿[4]。
目前,国内外关于可召回机制方面的研究仍处于探索阶段。在国外,Gallego和Kou[5]构建了一个两阶段的可召回机制下的收益优化模型,并求解出可召回机制中的可召回机票的最优分配数和召回可召回票的召回补偿价格所满足的条件,同时指出可召回机制对于高需求航线的舱位控制策略。在国内,首先是南京航空航天大学的朱金福、周艳、高强[6]等对航空收益管理的可召回制度进行研究。桂云苗、高强和孙刚[7-9]等建立数学模型与收益管理系统结合,在航空公司的可召回票的最优数量分配上提供了非常有利的决策。钟之阳和李金林[10-12]对于不同的情况下的可召回机制的舱位控制运用动态规划方法建立优化模型并求解。
在收益管理决策中,乘客的选择行为(Consumer Choice Behavior),即乘客如何在各种同航班机票中作出购买决策,是非常必要的加以考虑的一个因素[13]。在传统的收益管理模型中,往往都是假设各个等级舱位的乘客需求是相互独立的,通常都是直接假设出每个等级舱位的乘客需求量。
针对上述的情况,本文将可召回机制与乘客选择行为相结合。首先建立三阶段销售的可召回机制下的舱位控制模型,在此基础上考虑乘客选择行为,建立离散选择模型,同时与传统收益管理模型比较分析,发现实施可召回机制可使航空公司实现风险对冲套利,最后给出数值算例,验证本文优化模型的优越性。
1 可召回舱位控制机制模型
本文假设航空公司将某个航班的舱位机票分为三种:可召回票、低等级舱位票、高等级舱位票。三种票分为三个阶段销售:第一阶段为(0,T1)时段,在这一阶段首先销售可召回票;第二阶段为 (T1,T2)时段,在这一阶段销售低等级舱位票;第三阶段为(T2,T3)时段,在这一阶段销售高等级舱位票,如果在第三阶段高等级舱位票的实际乘客需求数高于剩余可利用舱位数,那么航空公司可以根据实际乘客需求数召回之前第一阶段销售的可召回票,并且对召回的乘客给与补偿。
进一步假设:
(1)航空公司采取召回补偿的方式是召回前补偿,并非是召回时补偿;航空公司在订座前制定可召回机制的相关条款,即被召回的每位乘客可获得的补偿为P=PL-PK。
(2)航空公司只有认定其实施可召回机制后的期望收益高于传统管理模式收益后才会实施可召回机制,即PH+PK-PL>PL。
(3)低等级舱位和高等级舱位的乘客需求是服从正态分布,且DL和DH相互独立。乘客对可召回票的需求DK是随机分布的,且乘客对于可召回票的第一张需求概率为1,即航空公司总是可以售出至少一张可召回票。
(4)航空公司的各种机票价格满足PK (5)航空机票都是通过互联网进行销售,即实施可召回票的成本极小,可忽略不计。 (6)不考虑超售、No-show、Go-show、乘客取消的情形。 本文将使用的变量如下: c:航空公司该航班各等级舱位总和(总票数);DK:航空公司可召回票的需求数;DL:航空公司低等级舱位的需求数;DH:航空公司高等级舱位的需求数;PK:航空公司可召回票的票价;PL:航空公司低等级舱位票的票价,同时也是召回可召回票的补偿价格(即召回的乘客可以获得固定单位 (P=PL-PK)的补偿额度);PH:航空公司高等级舱位票的票价;K:航空公司在第一阶段分配的可召回票舱位数;VK:航空公司在第一阶段销售的可召回票舱位数;LK:航空公司在第二阶段分配的低舱位数,LK=θ(c-VK),其中0≤θ≤1,且θ由航空公司根据传统二阶段收益管理方法来确定;SK:航空公司在第二阶段销售的低等级舱位数;HK:航空公司在第三阶段分配的高等级舱位数;WK:航空公司在第三阶段销售的高等级舱位数;QK:航空公司在第三阶段召回的可召回票舱位数。 根据上述所有的条件,于是,能够得出航空公司各阶段销售情况如表1所示: 表1 可召回机制各阶段销售情况 因此,航空公司某航班在引入可召回机制后总收益包括四个部分:(第一阶段)销售可召回票的收益、(第二阶段)销售低等级舱位票的收益、(第三阶段)销售高等级舱位票的收益和召回可召回票的成本。即,航空公司某航班的总收益RK为: 若所有想要购买机票的乘客都有其保留价格(Reservation Price),那么低等级舱位乘客只有在航空公司的低舱位售价PL小于他们的保留价格BL时才会发生购买行为,否则继续等待;同样高等级舱位的乘客只有在航空公司的高舱位售价PH小于他们的保留价格时才会发生购买行为,否则继续等待。面对不同价格的舱位票,不同类型的乘客根据个人意愿喜好选择购买,或者依据个人决策选择继续等待。因此,乘客选择流程图如图1所示: 图1 乘客选择流程图 假设低舱位和高舱位的乘客到达率是服从正态分布,低舱位乘客到达率服从均值为μL,0、标准差为σL,0的正态分布,高舱位乘客到达率服从均值为μH,0、标准差为σH,0的正态分布,那么低舱位乘客需求DL的均值为同样,高舱位乘客需求DH的均值为并且低舱位和高舱位乘客需求是服从正态分布。本文假设参数μL,0和μH,0是随机不确定,本小节模型的乘客选择行为问题是利用离散选择模型来解决,乘客选择某个等级舱位票的概率通过对乘客效用函数的计算来确定。 定义1:对于已给定全体舱位票集合S,乘客选择第i种舱位票的效用函数为: 其中:ui是乘客选择购买第i种舱位票的平均效用,ηi是乘客选择购买第i种舱位票的随机效用误差。如果乘客没有发生购买行为的效用为: 随机效用误差ηi的存在是因为效用函数中有难以确定的属性因素,如乘客的个人喜好、收入水平等原因会影响乘客效用函数值的确定。 定理1:由于所有想要购买机票的乘客是具有理性的判断,每位乘客都会选择自己能够得到最大效用值的舱位票,则乘客选择第i种舱位票的概率为: 假设ηi(i∈S)是相互独立的,并且服从Gumbel分布,则可得到: 令权重ωi=eUi,i=0,1,2,…,n,因此乘客选择购买第i种舱位票的概率可以表示为: 显而易见,eUi是随着Ui的增加而增加,U0是表示乘客没有购买机票的效用数,因此可以得到U0=0,于是乘客没有购买机票时权重ω0=1。 假设第i种舱位乘客的到达概率为λi,乘客选择概率由乘客的到达率λi和选择权重ωi来决定的。在实际情况中,航空公司通过历史售票数据用数学方法进行估算乘客的到达率λi和选择权重ωi。本文主要研究乘客选择行为和可召回机制结合起来的模型,所以在此忽略了关于参数估计的讨论,而直接假定ωi的估计值,在此假设乘客的选择权重ωi与购买机票的时间无关,同时,假设影响乘客选择购买第i种舱位票行为的属性只有机票价格因素,即只有机票的价格影响乘客选择权重。假定的ωi的估计值如表2所示: 表2 机票价格与乘客选择权重 对于第一节中可召回票的销售量VK的计算,要从第一阶段中乘客购买可召回票的概率出发。如果乘客购买可召回票,那么他们必须承担可召回票被召回的风险成本,因此他们的保留价格必定是PK 假设保留价格BK是服从[a,b]的均匀分布,PK∈[a,b),PL∈(PK,b),那么: 在传统收益管理模式是没有可召回票的存在,以下讨论传统模式与可召回机制的收益比较分析。传统模式的收益管理模型中K=0,机票分为低舱位票和高舱位票。那么其收益模型为: 所以,航空公司某航班引入可召回机制后与传统收益管理模式的收益变化为: 通过上式比较可以得出,航空公司某航班通过引入可召回机制与传统收益管理模式相比,航空公司的收益是增加的。而且,从前文的理论分析中可以看出,这种收益的增加对航空公司而言是几乎没有风险的,也就是可以理解为这是一种套利行为。换个角度来说,在引入可召回机制以后,相对于传统的收益管理模式而言,航空公司某航班能够获得一种将风险对冲的实物期权。根据前面的分析,航空公司在选择是否召回与不召回,只有当航空公司经判断认为实施可召回票的潜在收益大于传统模式的收益,也即满足时,航空公司才会实施召回来增加其收益。 以下通过不同的数值假设来分析航空公司某航班的可召回机制的作用。假设航空公司某航班的舱位总数C=300,购买可召回票乘客的保留价格BK是服从[0,80 ]0的均匀分布。通过前面的模型计算结果如表3所示: 表3 与传统模式收益比较 根据第二节的讨论,乘客选择购买第i种舱位票行为的决定属性只有价格因素,并且给出了机票的价格与乘客选择权重的关系表格,那么根据表2和式(6)可以计算出乘客选择某种舱位票的概率,然后根据式(1)可以计算出可召回机制的收益值,结果如表3所示。 于是,通过数值计算可以明显看出航空公司在引入可召回机制后比传统收益模式能够获得更多的收益,其大约能在2%~9%之间。从表3中还可以看到当PK=350,PL=500时可召回票的销售量最少,而且可召回票价与低舱位票价相差越大越容易购买可召回票,这是因为可召回票价与低舱位票价相差越大,乘客购买可召回票最后能得到的补偿越高。同时通过表3还可以看出当低舱位票价和高舱位票价差距增大时,或者高舱位票价增加时,航空公司的收益有明显的增加。因此,在需求旺季时,航空公司低舱位的分配数通常不会留有太多,航空公司可以通过实施可召回机制来提高收益。 本文将三阶段可召回机制模型与乘客选择行为结合起来,在建立三阶段销售的可召回机制下的舱位控制模型的基础上,结合乘客选择行为的思想,建立乘客离散选择模型,同时与传统收益管理模型比较分析,发现实施可召回机制可使航空公司实现风险对冲套利,最后给出数值算例,验证本文优化模型的优越性。但是本文模型存在着不足之处,本文假设乘客选择某种舱位票行为的决定属性只有价格因素,但是在实际情况中乘客选择行为也是受时间因素影响的。
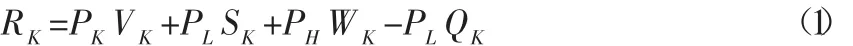
2 基于乘客选择行为下的优化模型







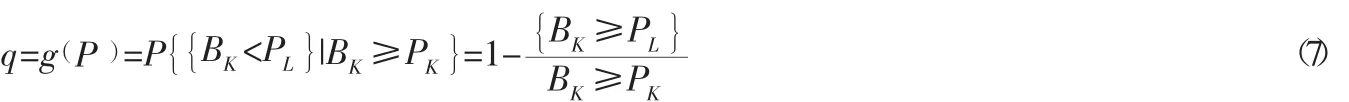

3 模型分析



4 数值分析

5 结 论
