特殊教育与普通教育的兼容性检验——基于上海市1991-2013年的数据

刘孝斌

（中共湖州市委党校 经管教研室，浙江 湖州 313000）

特殊教育与普通教育的兼容性检验
——基于上海市1991-2013年的数据

刘孝斌

（中共湖州市委党校 经管教研室，浙江 湖州 313000）

在特殊教育体系建设的大背景下，以上海市1991-2013年的时间序列数据为样本，对特殊教育和普通教育的兼容性进行协整检验．结果显示：普通教育对特殊教育产生了显著的正向作用；在普通教育和特殊教育之间不存在格兰杰因果关系．得出的启示：通过普通教育提高整个社会对特殊教育的认知度是推动特殊教育发展的根本之策．

特殊教育；普通教育；上海

国务院2014年颁布了《特殊教育提升计划（2014-2016年）》，这意味着特殊教育迎来了一个重要的发展契机.在整个国民教育体系中，特殊教育占据着特殊的地位，它不仅代表着国家的人文关怀，也彰显着教育作为立国之本的阔大涵养.然而一个值得注意的现实是：在教育资源总量给定的前提下，教育资源在普通教育与特殊教育之间的分配呈现的是一种此消彼长的关系.因此，作为国民教育体系的两大组成部分，普通教育与特殊教育的兼容性如何？目前对特殊教育的研究主要有3个方向：一是研究国外特殊教育的启示[1，2]，二是国内特殊教育的现状[3，4]，三是特殊教育本身的影响因素研究[5，6].目前对普通教育的研究主要集中于国外普通教育的启示[7-9].目前关于普通教育和特殊教育的研究大多各自沿单线前行，两者鲜有碰头.从现实从发，普通教育与特殊教育确实存在诸多交汇之处，例如普通教育学校会开设特殊教育专业培养特殊教育从业者.本文从关于普通教育与特殊教育兼容性疑问出发，选择上海市1991-2013年的时间序列数据为样本对两者的兼容性进行实证检验，以期为两者兼容性的疑问寻觅答案.

1 模型、变量与数据

在参照文献[10-12]等人研究成果的基础上，本文构建（1）式计量模型检验特殊教育与普通教育的兼容性：

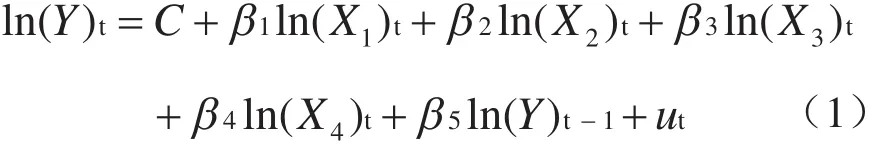
模型中，特殊教育（Y)为被解释变量；普通教育（X1）为解释变量；居民生活水平（X2）；科技发展水平（X3）；金融发展水平（X4）为控制变量.同时为了将特殊教育的其他影响因素（主要是无形的、难以量化衡量的因素，诸如制度、人文习俗、历史传统等）纳入考察范围，本文将这些因素打包放在滞后一阶的被解释变量（Y）t-1中.各变量的符号、含义、衡量指标等见表1.

本文选取上海市1991-2013年的时间序列数据为样本，数据来源于《上海统计年鉴》.变量的描述性统计见表2.

表1 变量说明

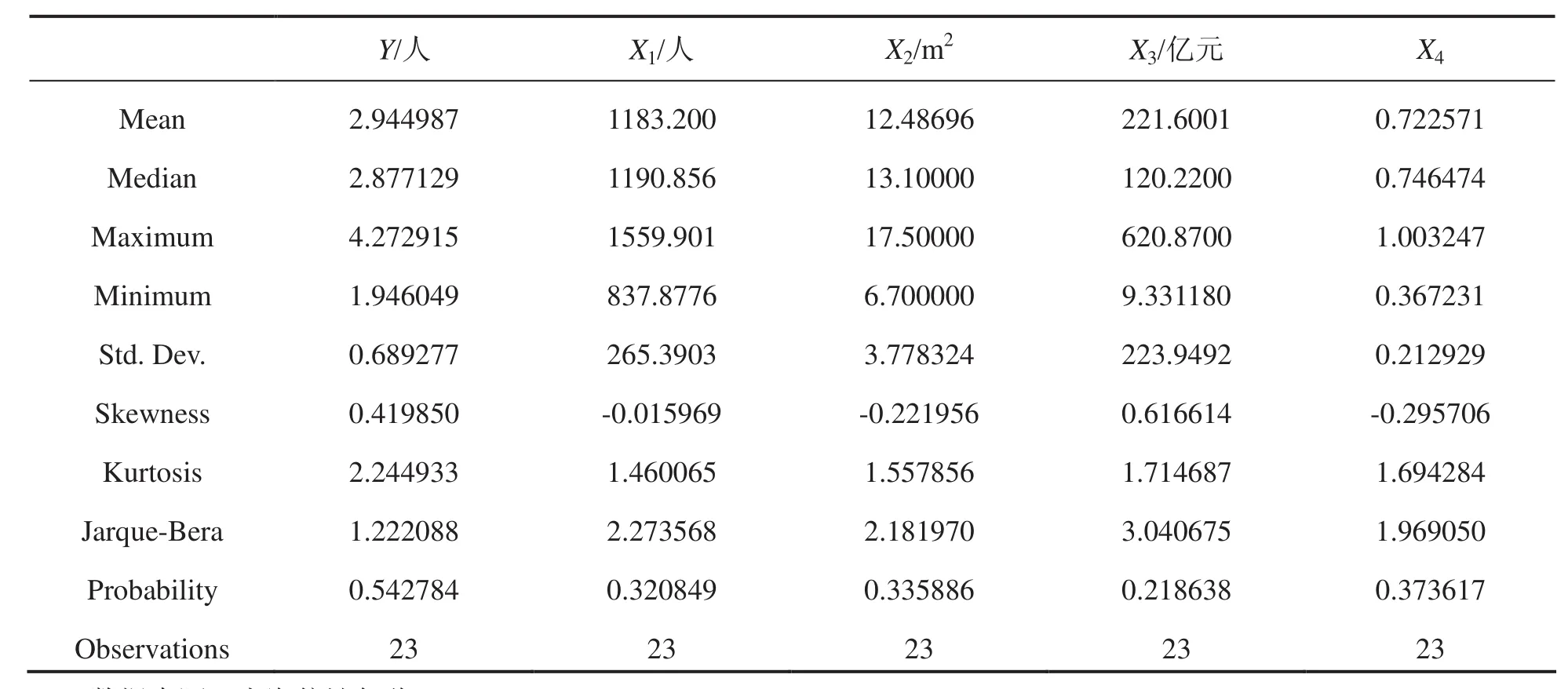
表2 变量的描述性统计

2 实证检验

2.1 ADF检验

ADF检验是协整分析的重要步骤，主要的目的是检验伪回归现象.ADF检验形式为（c，t，r），c表示存在截距；t表示存在时间趋势；r表示滞后的阶数.例如（0，t，3）表示无截距、有时间趋势、滞后阶数为3；（c，0，4）表示有截距、无时间趋势、滞后阶数为4，依次类推.检验结果显示lnY、lnX1、lnX2、lnX3、lnX4非平稳.对以上变量进行一阶差分，

ΔlnY、ΔlnX1、ΔlnX2、ΔlnX3、ΔlnX4即为相应变量的一阶差分值，他们都在10%的临界值上平稳，且他们的单整阶数相同，不存在伪回归问题，可以进行协整检验.检验结果见表3.

2.2 协整检验

2.2.1 根据无约束VAR模型确定最佳滞后阶数

确定无约束VAR模型最佳滞后阶数需要从较大的滞后阶数开始，并结合FPE、LR 、SC 、AIC 、HQ值等衡量标准进行选择.考虑到样本数量的大小，本文将最大滞后阶数定为6，从6开始，FPE、LR 、SC 、AIC 、HQ确定的最佳滞后阶数为0，见表4.

2.2.2 协整向量个数的确定

通过Johansen的迹统计量协整检验得出的结果见表5.检验结果表明变量之间有5个协整方程，即协整向量个数为5.

2.3 协整方程

采用var模型估计出来的协整方程表达式如下：

估计结果的可信度检验见表6，表6中的检验结果表明：方程的拟合优度很好（可决系数达到0.965657，调整的可决系数也达到了0.954925），与此同时方程总体的显著性比较理想（F-statistic为89.97783，Log likelihood为38.04403），因此协整方程的估计结果可信度较高.

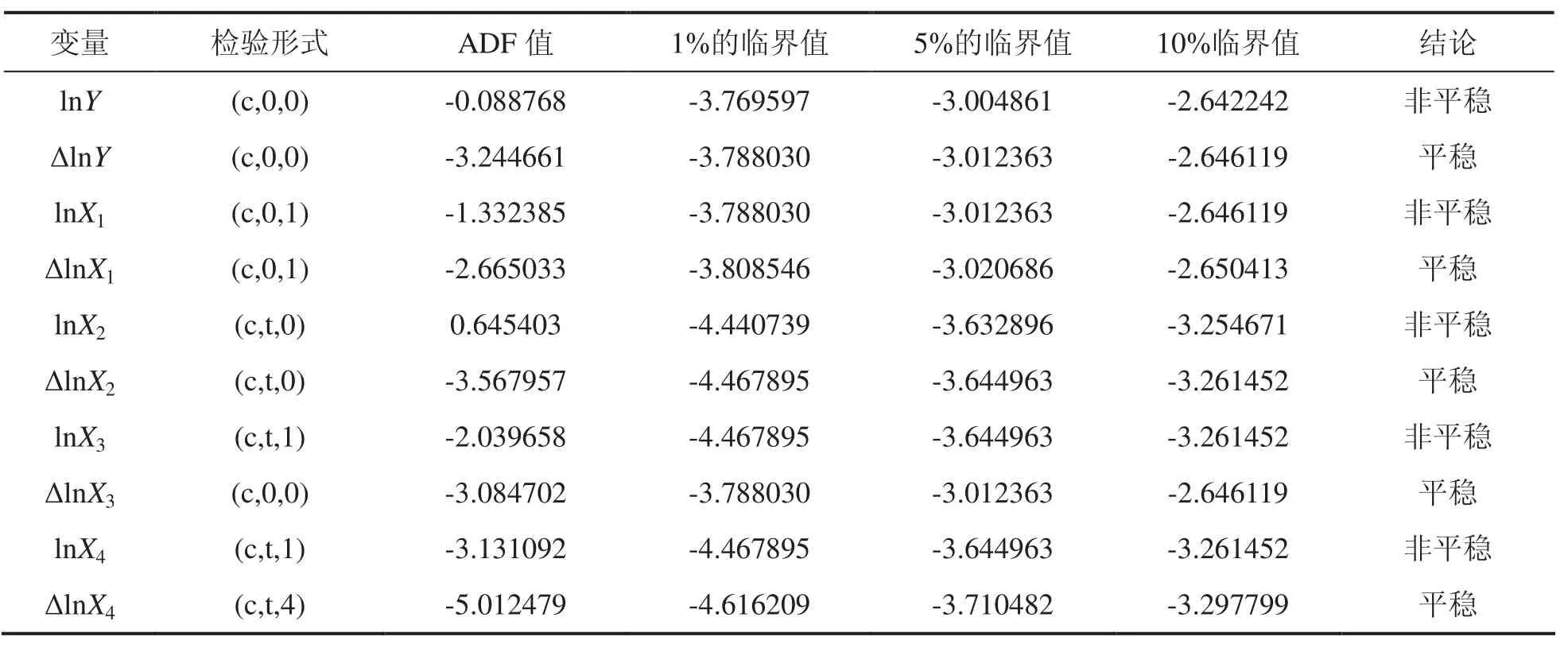
表3 ADF检验结果①

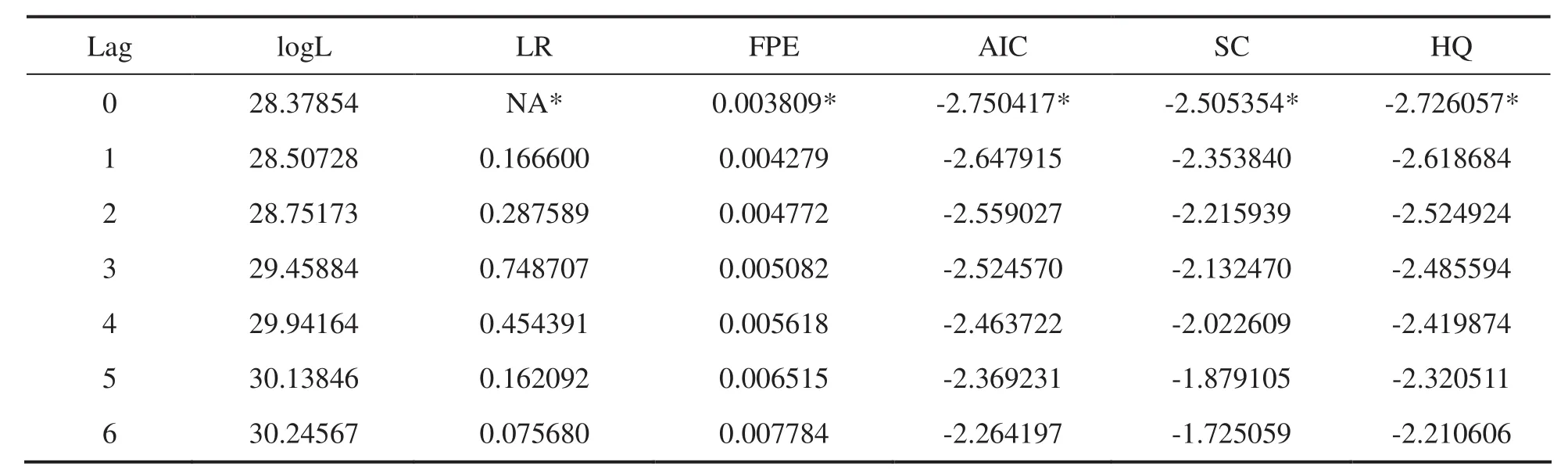
表4 无约束 VAR模型的最佳滞后阶数

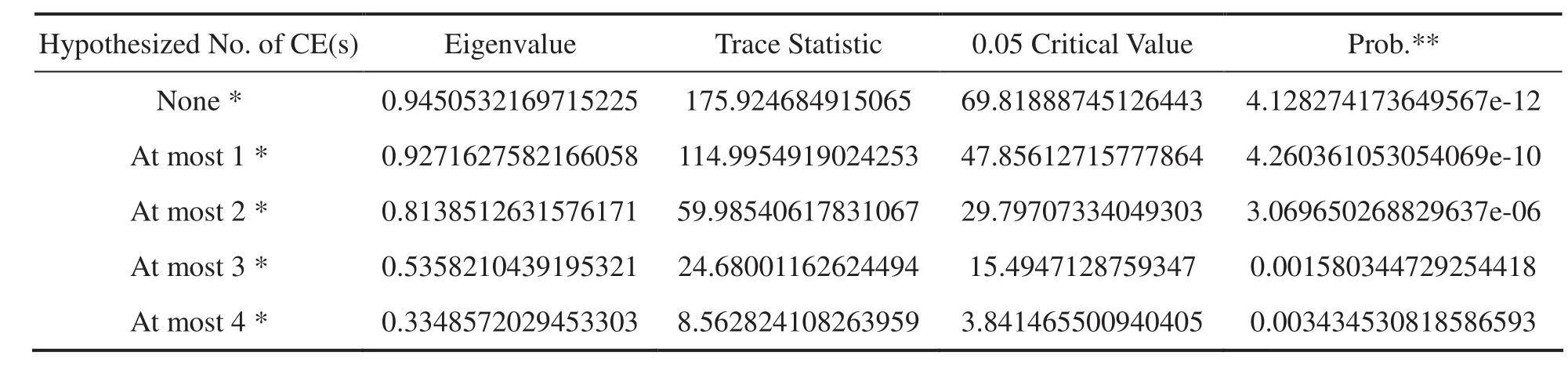
表5 Johansen的迹统计量协整检验

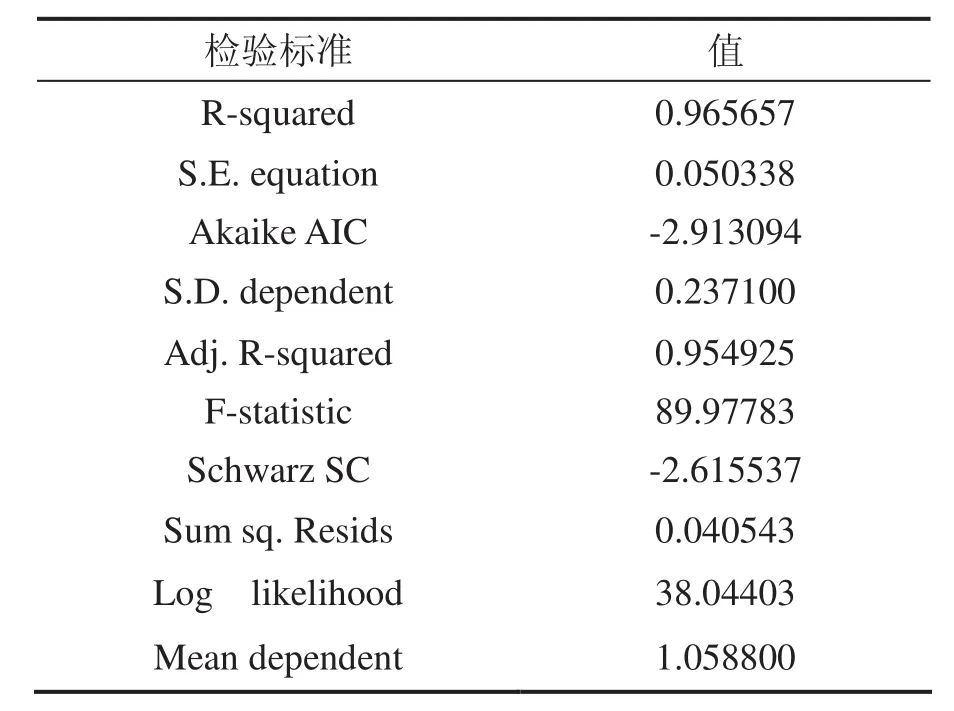
表6 协整方程估计结果的可信度检验

2.5 格兰杰因果检验

变量之间的两两格兰杰因果检验，结果见表7.在格兰杰因果检验中，原假设 lnY does not Granger Cause lnX1的F检验值为3.686336610323985，P值为0.04822727951692598，在5%的显著性水平上显著.因此得出的结论为：特殊教育不是普通教育的格兰杰原因.原假设 ln X1does not Granger Cause lnY 的F检验值为12.2354420344378，P值为0.0005967855919051368，在1%的显著性水平上显著.因此可以得出结论：普通教育也不是特殊教育的格兰杰原因.

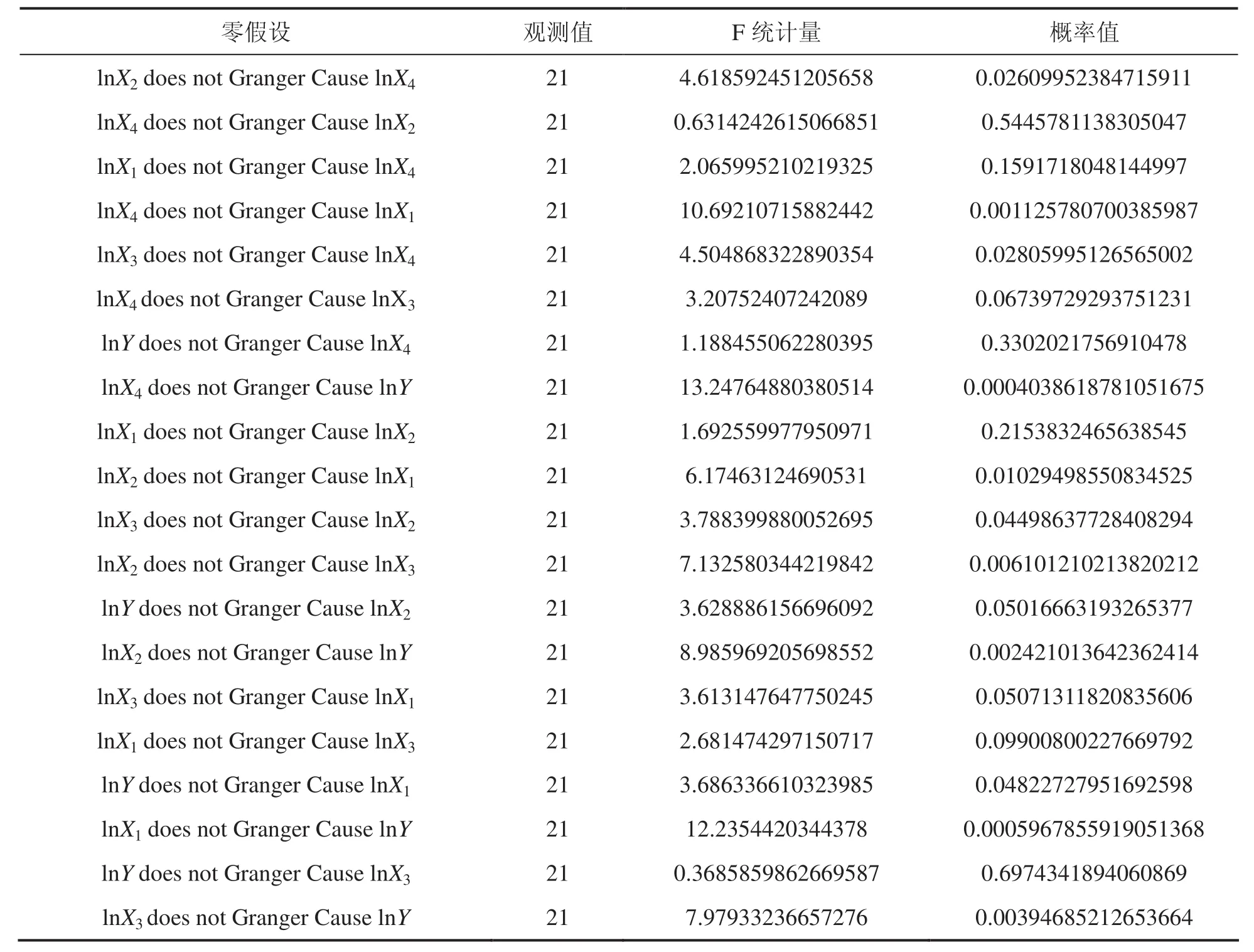
表7 格兰杰因果检验

3 结 论

1）普通教育对特殊教育产生了显著的正向影响，影响系数为1.435946361226719，t值为3.47160.这表明普通教育的发展会带动特殊教育发展，成为特殊教育的发展推动力.这一结论符合传统预期，普通教育发展的结果是公民素质的提升，从而促使整个社会对特殊教育的认知度提高，特殊教育因此获得更多的发展机会和资源.这给我们的启示在于：在普通教育中加大对特殊教育的普及力度，通过设置特殊教育知识性课程或者定期举办特殊教育培训班次，扩展特殊教育的社会影响和公众认同感.

2）科技发展水平对特殊教育产生了显著的正向影响，影响系数为0.1536234194600386，t值为1.95301.因此科技进步为特殊教育的发展注入了动力.这给我们的启示在于：加大科技对特殊教育的支持力度，从设备、器材、教学工具等方面着手扩大特殊教育的科技应用范围，同时更为重要的是追随科技革命大势及时更新特殊教育理念，从而推动特殊教育对新技术的适应性和延展性.

3）以人均居住面积衡量的居民生活水平对特殊教育产生了负向影响，但是不显著，影响系数为-0.2531547562840019，t值为-1.13096.这表明居民生活水平的提高对特殊教育的发展产生了轻微的阻碍作用，居民生活水平的提高没有与特殊教育认知度的提高保持同步.不过居民生活水平不是特殊教育的主要影响因素，它对特殊教育的影响不显著.

4）金融发展水平对特殊教育产生了显著的正向影响，影响系数为0.2009387232361736，t值为2.11385.因此金融发展推动了特殊教育的发展.以滞后一阶特殊教育代表的其他影响因素（主要是无形的、难以量化衡量的因素，例如制度、人文习俗、历史传统）对当期的特殊教育产生了显著的正向影响，影响系数为0.3571209153749126，t值为2.51007.这意味着一些无形、难以量化衡量的因素对特殊教育也发挥着推动作用.不可否认，教育制度、人文习俗以及历史传统对于特殊教育有着积极的影响，一个重视教育的地区比一个不重视教育的地区更能激发特殊教育从业者的教育热情.这给我们的启示在于：特殊教育的发展不仅依赖于硬环境（物质资源）的改善，还要依赖于软环境的改善.因此打造一个容纳、激励特殊教育的软环境对特殊教育而言非常必要.

在格兰杰因果检验中，特殊教育不是普通教育的格兰杰原因，普通教育也不是特殊教育的格兰杰原因.于是，在特殊教育和普通教育之间不存在格兰杰因果关系.这一结论意味着目前的特殊教育和普通教育之间尚未形成一个良性互动机制，从而导致两者处在割裂的发展状态.这给我们的启示在于：特殊教育在未来发展过程中需要逐步探索建立与普通教育的良性互动机制，从而借助于普通教育的发展促进自身的发展.

[1] 谢敬仁，钱丽霞，杨希洁，等.国外特殊教育经费投入和使用及其对我国特殊教育发展的启示[J].中国特殊教育，2009（6）：17-24.

[2] 兰岚，兰继军，吴永怡.台湾地区特殊教育及对大陆特殊教育发展的启示[J].中国特殊教育，2008（12）：18-22.

[3] 王雁，李欢，莫春梅，张瑶.当前我国高等院校特殊教育专业人才培养现状分析及其启示[J].教师教育研究，2013，25（1）：28-34.

[4] 赵小红.中国特殊教育学校教师队伍状况及地区比较——基于2001-2010 年《中国教育统计年鉴》相关数据[J].中国特殊教育，2012（8）：49-59.

[5] 赵斌，李燕，张大均.川渝地区特殊教育学校教师职业幸福感状况及影响因素的研究[J].中国特殊教育，2012（1）：42-46.

[6] 王姣艳，王辉.特殊教育教师职业认同的影响因素研究[J].中国特殊教育，2013（1）：52-57.

[7] 陈利民.哈佛大学新世纪的普通教育[J].高等工程教育研究，2007（2）：123-126.

[8] 张文军.英国14-19岁普通教育考试制度与高校入学机制的关系研究[J].比较教育研究，2004（7）：47-51.

[9] 孙曼丽.构建高等职业教育和高等普通教育间的桥梁——美国社区学院“转学教育”复兴再探[J].外国教育研究，2011,28（7）：11-16.

[10] 毛建青.影响高等教育规模的主要因素及其协整关系——基于时间序列数据的分析[J].北京师范大学学报（社会科学版），2009（2）：114-119.

[11] 刘云忠，徐映梅.我国城乡教育差距与城乡居民教育投入差距的协整研究——基于1990～2005年的数据分析[J].教育与经济，2007（4）：42-46.

[12] 梁军.教育发展对中国经济增长影响的实证分析——基于1980～2006年的时间序列数据[J].教育学报，2009,5（2）：101-108.

[13] 顾定倩，杨希洁，江小英.从政策解读我国特殊教育教师专业标准的建构[J].中国特殊教育，2014（3）：71-74.

[14] 彭霞光.中国特殊教育发展现状研究[J].中国特殊教育，2013（11）：4-7.

[15] 时磊，杨德才.“分权计划经济”时期的普通教育发展：经济史的再考察[J].南京大学学报（人文科学社会科学），2014（1）：49-59.

[16] 朱新生.试论职业教育与普通教育的相互沟通[J].教育发展研究，2002（11）：92-95.

[17] 罗楚亮.城镇居民住房面积的不平等——基于2000年和2005年人口调查的经验分析[J].学海，2014（1）：80-90.

[18] 窦尔翔，何小锋.教育制度、教育融资与教育金融制度安排[J].教育发展研究，2006（7A）：35-39.

[19] 刘孝斌.金融市场现代化背景下金融发展影响文化产业的实证分析[J].上海金融学院学报，2014（5）：44-53.

[20] 李桂花，曲家伟.论科技进步与教育发展良性循环的实现[J].理论学刊，2015（2）：83-89.

[21] 李倩.基于动态空间面板模型的中国区域创新集聚研究[J].中国经济问题，2013（6）：56-64.

[22] 刘孝斌.选择性迁移、创新集聚与经济转型升级[J].甘肃行政学院学报, 2014（2）：81-91.

Compatibility Test of Special Education and General Education—Based on Data from 1991-2013 in Shanghai

LlU Xiaobin

（CPC Huzhou Municipal Party School, Huzhou, Zhejiang 313000, China）

Under the background of building special education system, this paper takes time-series data from 1991 to 2013 years in Shanghai as a sample to test the compatibility of special education and general education. Results show that: general education has significant and positive effect on special education; and there is no Granger Causality between special education and general education. According to the empirical test, the paper comes to the conclusion that the fundamental policy of promoting the development of special education is to improve awareness of the whole society for special education through general education.

special education; general education; Shanghai

G76

A

1672-0318（2016）01-0071-06

10.13899/j.cnki.szptxb.2016.01.015

2015-07-07

刘孝斌（1986- ），男，湖南常宁人，助教，经济学硕士，研究方向为金融市场、产业经济.