基于改进Gordon方程的RCS快速算法
2016-11-14徐灿,李智
徐 灿, 李 智
(1. 装备学院 航天装备系, 北京 101416; 2. 装备学院 航天指挥系, 北京 101416)
基于改进Gordon方程的RCS快速算法
徐灿1,李智2
(1. 装备学院 航天装备系, 北京 101416;2. 装备学院 航天指挥系, 北京 101416)
Gordon方程是物理光学法计算平面面元雷达散射截面积(RCS)的一种围线积分实现形式,其运算量与复杂目标拆分面元边的数量成正比。首先,通过对Gordon方程计算相邻平面面元RCS表达式的分析,证明了同一平面内两面元的公共边对RCS计算没有贡献的推论。其次,提出在预处理阶段利用排除法筛选并剔除公共边,简化RCS计算过程并避免引入新的计算量。由于消除了目标三维模型面元化处理过程中所形成的公共边,计算速度提高33%以上。最后通过2个实验算例验证了所提方法的正确性。
Gordon方程;围线积分;公共边
雷达散射截面积(RCS)是目标雷达特性的核心物理量,RCS估计在目标识别、探测及隐身设计上具有重要作用[1]。当目标尺寸远大于雷达波长时(2πa/λ>20,其中a为目标特征尺寸,λ为雷达波长),此时目标称为电大尺寸目标[2],由于目标各部分之间相互作用弱,高频法得到广泛应用[3-4]。高频法根据求解电磁场分量的不同,又分为几何光学法、物理光学法、一致性绕射理论法等[5],其中物理光学法较几何光学精度更高,较一致性绕射理论法更易实现实时性,因而得到快速发展[6]。实际应用物理光学法时,利用三维建模软件建立目标三维模型,将目标拆分为微小面元并逐个面元计算散射场(称为“有限元法”)。目标拆分处理后,Gordon方程可以较好地解决RCS计算问题[7],但该方法由于直接处理三维建模软件拆分的面元,没有对各面元进行预处理,计算效率较低[8]。本文针对这一问题展开研究,提出对拆分后的面元进行预处理,剔除无效分量以提高运算速度。
1 数值法计算复杂目标RCS
在所有的散射中,一个基本问题是确定目标上的感应电磁流,只要求得感应电磁流,散射场和RCS值就可以用物理光学法进行计算。物理光学法是一种高频方法,它用充当散射场激励源的感应表面电磁流来代替目标,可以直接获得RCS均方根的表达式。Gordon将物理光学法中对微小面元的积分操作转换为围线积分,更易于实现。将三维模型拆分为若干小的面元是当前多数三维建模软件都具备的功能,计算M边形微小面元RCS均方根的Gordon方程如下:
(1)
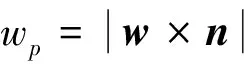
式(1)是目前Gordon算法的常用实现形式,采用的是逐边计算而后矢量相加的方法。计算每个小面元时需要对该面元的3个边分别进行计算实现围线积分。设一个复杂目标被拆分成L个小的面元,这L个面元都能为入射电磁波照射且互相不遮挡。则总的目标电磁散射强度可以表达为
当面元数增加时,式(1)的调用次数也将增多,计算复杂度提高。降低复杂度的最直接方法就是减少式(1)的调用次数。以下将通过分析同一平面内公共边(同一平面内两小面元的公共边)线积分的特点,而后给出优化方案。
2 对Gordon方程的改进处理
2.1目标RCS计算中的公共边
设目标拆分后存在一个平面部分,平面内包含若干平面多边形。此处以平面三角面元为例,顶点次序统一按逆时针顺序给出,取拆分后同一平面内具有公共边的2个相邻面元,如图1所示。
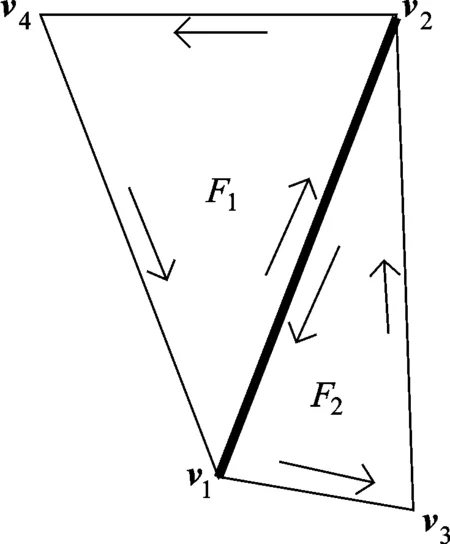
图1 同一平面内相邻面元的公共边(中间加粗部分)
面元F1的3个边分别是v1v2、v2v4和v4v1,边矢量表示为af1_1、af1_2和af1_3;面元F2的3个边分别是v2v1、v1v3和v3v2,边矢量表示为af2_1、af2_2和af2_3。
在逆时针的条件下,根据矢量性质得到
面元F1的RCS平方根由3条边的线积分构成,即式(1)中m=1,2,3的3部分,具体表示为
(2)
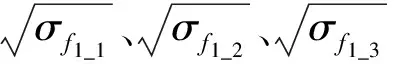
面元F2的RCS平方根同样可以由其3条边的线积分构成,即
(3)
式中,F1第一条边的线积分结果可表示为
(4)
F2的第一条边的线积分结果可表示为
(5)

(6)
该结果表明,同一面元内2个面元公共边散射强度矢量和为0,对总RCS没有贡献。虽然上述公共边对总RCS没有贡献,却占用了1/3的计算资源。既然总的散射强度与公共边没有关系,如果我们能够在计算前就将该面元的公共边剔除,那么计算量就会大大降低。
2.2目标三维模型公共边的标识
基于目标构型信息,提出公共边标识的步骤如下:
1) 计算所有面元的外法线矢量;
2) 取L×3的二维数组S[L][3],全部标记为0,作为公共边的初始标识数组:若某条边为公共边,则对应元素为1,否则为0;
3) 自第1个面元开始,确定公共边。
以第i(i=1,2,…,L)个面元为例说明判断过程。若该面元法线矢量为ni,遍历其他面元判断是否存在该面元的公共边。判断方法如下:
1) 取第j个面元,其外法线矢量为nj,若ni=nj,则初步判定2面元共面;
2) 在共面的基础上,判断第一个边是否为公共边:若第i面元的第一顶点与第二个顶点同时为第j个面元的顶点,则第一条边是公共边,记S[i][0] 为1;
3) 判断第二条边是否为公共边:若第i面元的第二个顶点与第三个顶点同时为第j个面元的顶点,则第二条边是公共边,记S[i][1] 为1;
4) 判断第三条边是否为公共边:若第i个面元的第三顶点与第一个顶点同时为第j个面元的顶点,则第三条边是公共边,记S[i][2] 为1;
5) 按照以上步骤,遍历除第i个面元之外的所有面元(j=1,2,…,L),完成对第i个面元公共边的判定;
6) 顺序遍历所有面元(i=1,2,…,L),完成对数组S的标识。
经过以上6步的操作,实现了对面元公共边的标识。一旦该边被标识为公共边,表示该边已被排除在RCS计算的范围之外,将不参与RCS的计算,故称之为排除法。对于由L个M边形组成的目标,公共边筛选的计算量为O(M2L2)。但公共边标识过程与电磁波入射方向及材料参数无关,仅取决于目标的三维构型,因此,上述操作可作为RCS计算前的预处理,实际参加RCS计算的是剔除公共边之后的简化模型,预处理操作不会给RCS的计算引入新的计算量。不经预处理,RCS计算量为O(ML),每条边均需经过6次浮点型矢量运算和同等次数的标量乘除运算,每剔除一条公共边即可减少2次Gordon方程的调用。对于目前广泛使用的三角面元拆分法,由于一个平面上的2个相邻面元必然拥有一个公共边,剔除该公共边后将使计算量减少33%,而考虑实际模型还存在3条边均为公共边的面元,计算速度将提高33%以上。对于处理能力有限的模拟器、弹载或星载处理器,这一改善有助于提高计算的实时性。
2.3计算目标RCS
在计算目标散射强度时,需要判断当前面元是否被电磁波照射,涉及一次遮挡与二次遮挡的判断,相关文献[5,8]已经有较为详细的描述,这里不再赘述。
对于不被遮挡的面元,可通过计算各个边长的线积分来实现RCS的计算,积分时被标识的公共边不参与运算。设剔除公共边后尚有Ls个边,第l个边的法线是nl,al是该边矢量,rl是指向该边中点的位置矢量,则总电磁散射强度的计算公式如下:
(7)
对于wp=0的面元,仍然使用式(1)来计算。
3 算法验证
以理想导体材料的立方体和圆柱为例,验证本文所提出的方法。图2是利用三维构型软件Creator构造的金属圆柱和金属立方体,其中,圆柱体长2 m,底边直径1.6 m,立方体边长4 m。
首先按照本文的方法进行公共边检测,检测结果如下:圆柱体共有320个三角面元,164个顶点。经公共边检测,960个边中有476个公共边(共面公共边),每次计算可节省50%的计算量;立方体包括144个三角面元,80个顶点。经公共边检测,432个边中有348个是公共边,每次计算可节省80.56%的计算量。
根据本文给出的方法,给出公共边去除前后的结果如图3所示。
公共边的剔除,使Gordan方程的调用次数大幅减少。为验证剔除公共边后RCS数值计算结果不受影响的推论,本文使用剔除公共边后的简化模型计算目标RCS,将计算结果与目前较为权威的RadBase软件生成结果对比。其中雷达中心频率3 GHz,选用垂直极化方式,结果如图4所示。

a) 金属圆柱体三维模型 b) 金属立方体三维模型图 2 利用目标文件信息重构的三维目标
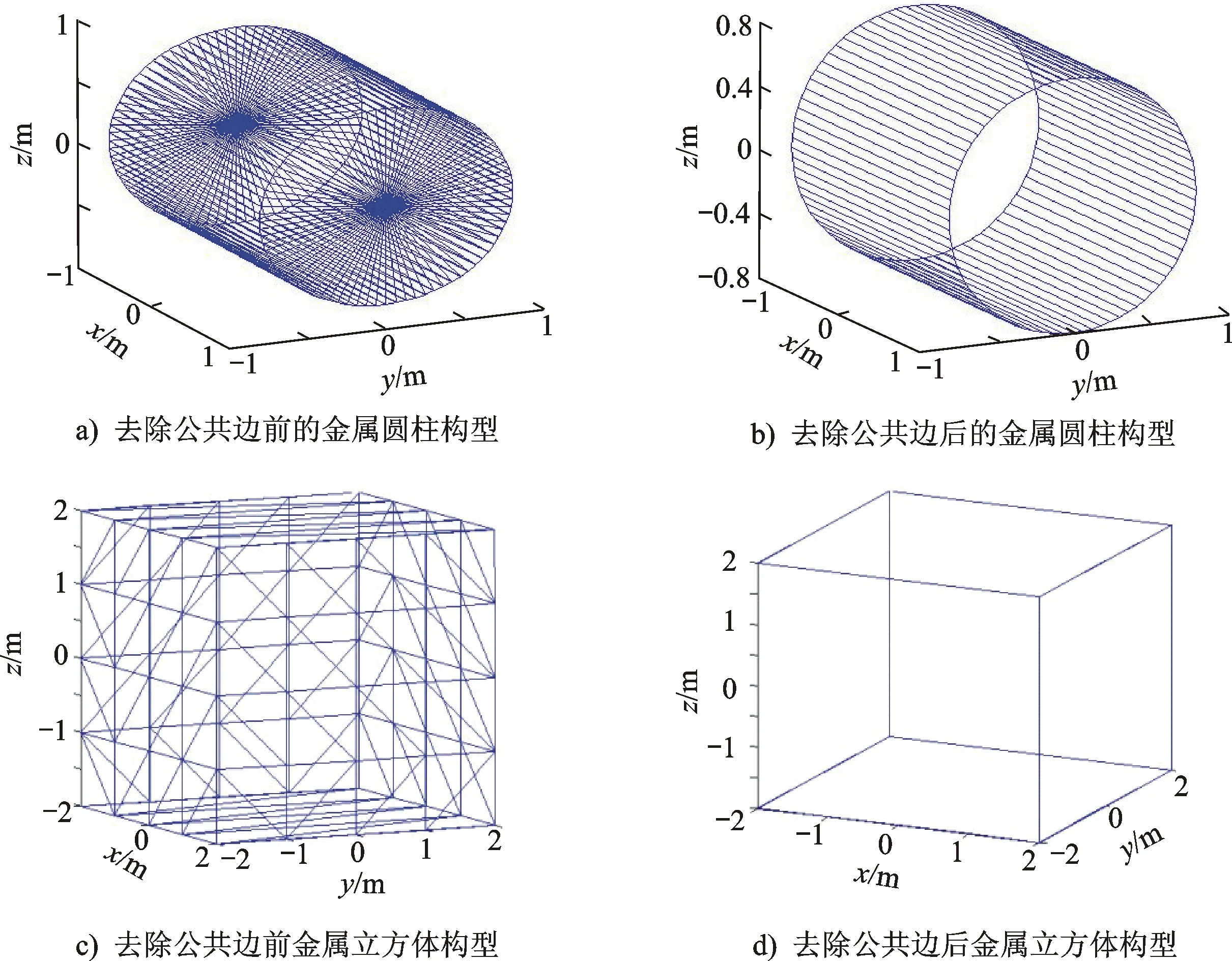
图3 目标公共边去除前后对比
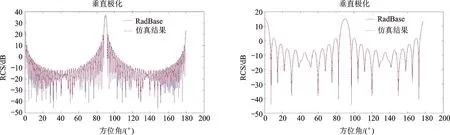
a) 金属圆柱RCS计算结果 b) 金属立方体RCS计算结果图4 利用边缘边计算目标散射强度
从图4给出的结果可以看出,剔除公共边后目标RCS的计算仍然是正确的。本文提出的方法,在显著降低运算量的条件下,仍能够保证计算精度,该方法有助于提高RCS计算的实时性。
4 结 束 语
本文根据Gordon方程的特点,提出在计算RCS之前对面元进行预处理,剔除对最终结果没有贡献的平面面元公共边。由于预处理可以在计算RCS前完成,不参加单次计算,有效降低了Gordon方程的调用次数,提高了运算的实时性。后续需要结合复杂目标的二次遮挡问题开展研究,提高所提方法的适用性。
References)
[1]庄钊文,袁乃昌,莫锦军,等.军用目标雷达散射界面预估与测量[M].北京:科学出版社,2007:97-114;242-264.
[2]黄培康,殷红成,许小剑,等.雷达目标特性[M].北京:电子工业出版社,2005:1-24.
[3]ELKING D M,ROEDDER J M.A review of high-frequency radar cross section analysis capabilities at McDonnell Douglas aerospace[J].IEEE Antennas and Propagation Magazine,1995,37(5):33-43.
[4]RIUS J M ,FERRANDO M,JOFRE L.High-frequency RCS of complex radar targets in real-time[J].IEEE Trans.Antennas and Propagation,1993,41(9):1308-1460.
[5]彭兰.改进的物理光学技术计算目标的雷达散射截面[D].西安:西安电子科技大学,2013:1-20.
[6]YIN H C,HUANG P K,LIU X G,et al.PO solution for scattering by complex object coated with anisotropic materials[J].Journal of Systems Engineering and Electronics,2003,14(2):1-7.
[7]GORDON W B.Far field approximation of Kirchoff-Helmholtz of scatter fields[J].IEEE Trans.AP,1975,23(5):590-592.
[8]YOUSSEF N N.Radar cross section of complex targets[J].Proceeding of the IEEE,1989,77(5):722-734.
(编辑:李江涛)
Fast Algorithm for Calculating RCS Based on Improved Gordon Equation
XU Can1,LI Zhi2
(1. Department of Space Equipment, Equipment Academy, Beijing 101416, China;2. Department of Space Command, Equipment Academy, Beijing 101416, China)
Gordon equation is a contour integral implementation to calculate the plane surface radar cross section (RCS) with physical optics method, and its computational cost is proportional to the number of edges of complex target split surface. First of all, through analysis on the RCS expression for the calculation of adjacent surface elements with Gordon equation, the paper proves the inference that the common side of two surface elements on the same plane has no contribution to the RCS calculation. Secondly, the paper puts forward screening and eliminating common sides with exclusion method in the preprocessing stage and simplifying the calculation process while avoiding introducing additional computation. Due to eliminating the common sides formed in the 3D target model surface element treatment process, computation speed is increased by over 33%. Finally, with two experiments the paper verifies the validity of the proposed method.
Gordon equation; contour integration; public side
2016-03-02
国家级资助项目(2015AA7046104)
徐灿(1985-),男,讲师,博士,主要研究方向为空间目标光电特性。452394317@qq.com
TN95
2095-3828(2016)05-0085-05
A DOI10.3783/j.issn.2095-3828.2016.05.018
李智,男,教授,博士生导师。
