窄条翼导弹俯仰机动中滚转失稳及其控制过程

王晓冰， 赵忠良， 李浩， 达兴亚， 陶洋

中国空气动力研究与发展中心 高速空气动力研究所， 绵阳　621000



窄条翼导弹俯仰机动中滚转失稳及其控制过程

王晓冰， 赵忠良*， 李浩， 达兴亚， 陶洋

中国空气动力研究与发展中心 高速空气动力研究所， 绵阳621000

窄条翼布局导弹通常具有复杂的横向气动特性，在大迎角飞行及快速机动中很容易诱发出现滚转非指令偏离和连续振荡，可能导致飞行失控，影响落点精度。为了研究窄条翼导弹俯仰快速机动对滚转失稳的诱发过程及滚转失稳对俯仰机动控制效果的影响，并验证三通道解耦控制方法的有效性，针对典型俯仰机动过程，分别利用2.4 m跨声速风洞虚拟飞行试验平台和耦合气动/运动/控制的一体化数值计算方法开展了相关研究。结果表明，风洞试验和数值模拟均成功预测了俯仰拉起和保持过程中的滚转自激失稳运动及其引起的纵、横向耦合运动，针对该机动过程，三通道解耦控制方法能够有效抑制滚转运动，保持姿态稳定。

窄条翼导弹； 滚转失稳； 虚拟飞行； 风洞试验； 数值模拟； 闭环控制

现代先进战术导弹通常有双鸭舵边条翼布局、三角前翼+梯形尾舵布局和窄条翼布局[1]等形式。其中，窄条翼布局在大迎角时不存在涡破裂，能够提供足够的转弯升力，具有优异的纵向气动特性，同时可以最大限度地利用弦向尺寸，减小展向高度，大大缩小在内埋武器舱中的占用空间。由于以上优势，很多现代先进战术导弹都采用了这种布局，如美国“标准”系列、法国MICA和德国IRST-T等，如图1所示。

同时，窄条翼布局导弹在较大迎角时存在由前体分离涡、窄条翼侧缘涡和尾舵分离涡构成的多涡系结构，横向气动特性复杂，在一些迎角可能会引起滚转静稳定点偏移或滚转阻尼丧失，加之导弹自身在滚转方向的转动惯量要远远小于纵向，很容易出现滚转方向的非指令自激运动，可能会导致导弹的姿态失控，影响落点精度。

图1　典型窄条翼布局导弹Fig.1　Typical missiles with strake wings

图2　窄条翼布局导弹自由摇滚试验结果(Ma=0.6)Fig.2　Free-to-roll test results for a missile with strake wings (Ma=0.6)

极限环摇滚运动是一种典型的滚转失稳运动。图2为典型窄条翼布局导弹自由摇滚的风洞试验结果[2]，其中实线为滚转角随时间的变化历程，点划线为试验过程中的不同迎角阶梯。可以看到，试验成功捕捉到了20° 和35° 迎角附近出现的极限环摇滚现象，并且在不同迎角时滚转静平衡点会发生跳变或偏离。图2中：α为迎角，γ为滚转角，t为时间。

目前，国内外学者对摇滚运动开展研究时，大多采用单自由度简化模型，即在滚转的单一自由度中研究摇滚运动的特性。而在实际飞行中，飞行器的多个自由度之间相互耦合、相互影响，构成复杂的非线性动力学系统[3-6]，单自由度简化研究模型将无法准确地对其进行描述，因此单自由度研究模型在理论上存在一定的局限性[7]。

为研究窄条翼导弹滚转失稳行为对快速转弯机动过程的影响，并进一步研究其控制方法，本文以典型窄条翼布局导弹典型俯仰机动过程为对象，基于2.4 m跨声速风洞虚拟飞行试验平台和耦合气动/运动/控制的一体化数值计算方法，研究了导弹在闭环控制拉起过程中的俯仰/滚转耦合特性及相应的控制方法。

1　试验方法

有关风洞虚拟飞行试验平台的组成、测量、控制和试验流程等内容已在文献[8-9]中作了详细介绍。利用该平台开展典型窄条翼导弹模型俯仰拉起过程中的滚转耦合现象以及多通道解耦控制方法的有效性试验研究，考核验证和对比分析气动/运动/控制一体化计算结果，以达到研究窄条翼导弹滚转失稳行为对快速转弯机动过程影响及其解耦控制方法的目的。

2　数值方法

2.1非定常流场计算方法

曲线坐标系下，忽略质量力、完全气体的无量纲化三维非定常Navier-Stokes方程守恒形式为[10]

(1)

空间离散采用的是基于多块结构网格的有限体积法，其中无黏通量的离散采用Roe的通量差分格式得到，界面处的流场守恒变量采用3阶迎风偏置的MonotonicUpwindSchemeforConservationLaws(MUSCL)插值得到；对非连续性问题的求解，使用Venkat限制器抑制数值振荡，对黏性通量则采用中心差分格式进行处理。对于非定常计算，采用由Jameson提出的双时间步方法，其中伪时间步采用Lower-UpperSymmetricGaussSeidel(LU-SGS)隐式计算格式。对边界条件，远场采用局部一维Riemann不变量计算，物面采用无滑移固壁边界条件。湍流模型采用Spalart-Allmaras(S-A)一方程湍流模型。同时采用多重网格方法来加速收敛，并采用基于MessagePassingInterface(MPI)的流场分块并行计算方法来提高计算效率。

2.2运动方程求解及气动/运动耦合策略

本文只考虑模型在弹体坐标系中绕质心的转动运动，相应的动力学和运动学方程为

(2)

目前，气动和运动方程的耦合求解策略主要包括全耦合、松耦合和紧耦合3类，其中松耦合和紧耦合方法由于实现简单、计算量小等特点，已经在国外得到了广泛应用，如德国[11-12]、英国[13]和美国[14-17]的相关学者均通过相关耦合方法，实现了飞行器常见机动过程的模拟，同时，国内也逐渐出现了相关研究[18-20]。

本文在非定常流场计算的双时间步推进过程中，采用三阶Adams预估校正法同步求解运动方程，其中显式预测步在物理时间推进过程中进行，隐式校正步在伪时间迭代中进行，可以达到气动/运动的紧耦合求解，保证耦合过程的二阶精度，从而可通过增大时间步长来缩短仿真时间[19]。

3　研究模型

研究模型采用典型钝头体-窄条翼-尾舵布局；导弹以“×”字形式飞行，定义此时滚转角为0°。图3定义了4片尾舵的编号及正舵偏的旋转方向，此时，各尾舵偏角可按照式(3)变换到弹体各通道，即

(3)

式中：δE、δR和δL分别为俯仰、偏航和滚转通道的舵偏角。当滚转角发生变化时，可根据投影关系进行修正。

图3　舵偏角定义(后视图)Fig.3　Rudder angles seen from the rear of a missile

开展风洞试验时，为便于模型在支撑横杆上进行安装，在确保其气动特性尽量相同的前提下，对弹身中部的弹翼进行了截断和改型，如图4所示。尾舵采用真实舵机，并由舵控仿真系统实现舵面的实时偏转。

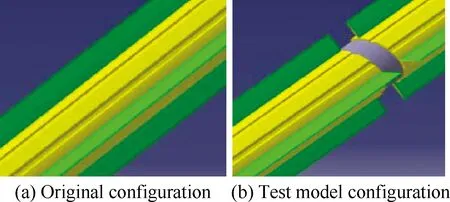
图4　试验模型的弹翼截断Fig.4　Strake truncation of test model

4　结果分析

4.1纵向气动特性计算

为验证流场计算方法，并初步研究窄条翼布局导弹的纵向气动特性，对Ma=0.6，基于1m长度的雷诺数Re=1.58×107条件下不同俯仰舵偏角的全弹纵向绕流开展了计算，迎角范围为0°～60°，俯仰舵偏角为0°和-10°。

对导弹外形划分结构网格，网格单元总量约600万。图5为模型空间网格分布情况。对不同舵偏，采用超限插值(TFI)方法自动生成对应网格，图6为不同舵偏角时的表面网格分布。实际计算表明，舵偏角不超过12.5° 时，生成的网格质量基本能够满足流场计算要求。图7为俯仰舵偏角分别为0° 和-10° 时全弹俯仰力矩系数Cm的计算与试验结果，可以看到动网格方法在较大迎角范围内均能较准确模拟导弹的舵面效率，但在迎角为20° 和40° 附近偏差较大，前者是由于窄条翼与尾舵存在强烈的涡系干扰，后者则是尾舵附近气流存在明显分离，对强非定常漩涡和大面积分离流动，本文采用的计算方法精度有所降低，但仍得到了与试验一致的变化趋势。

图5　模型空间网格Fig. 5　Volume grid of model

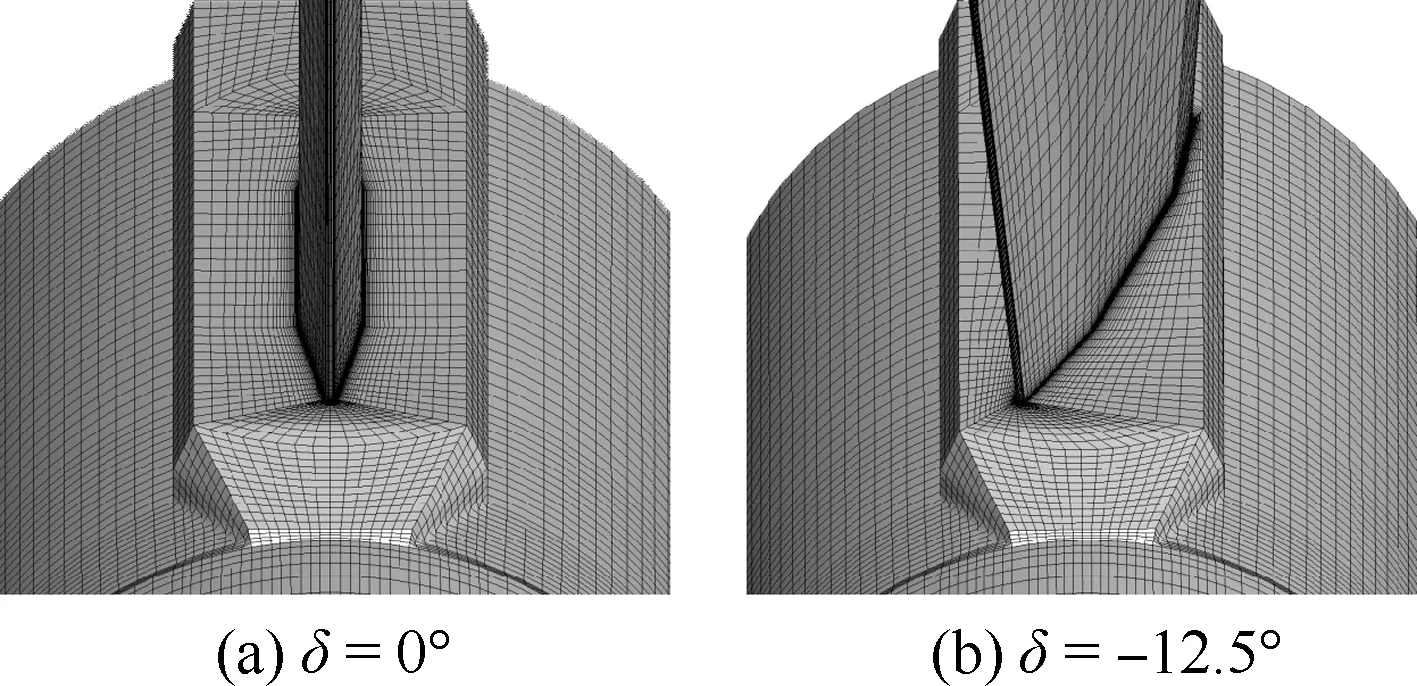
图6　不同舵偏角的表面网格分布Fig.6　Surface mesh of control surface at differentrudder angles

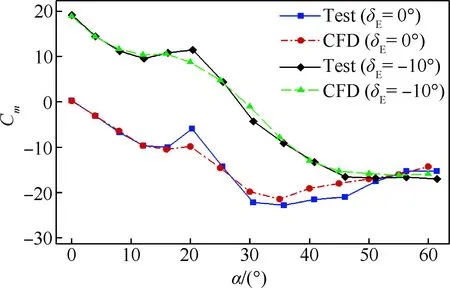
图7　俯仰力矩系数随迎角的变化(Ma=0.6)Fig.7　Pitching moment coefficient varying with different angles of attack (Ma=0.6)

4.2滚转无控时的俯仰/滚转耦合运动

考虑到计算网格对舵偏角大小的限制，选取导弹在水平来流中俯仰角θ由0° 快速拉起到25° 的机动过程开展研究。来流马赫数Ma=0.6，基于1m长度的雷诺数Re=1.58×107。

导弹在实际飞行过程中，通常采用俯仰、偏航和滚转通道解耦的三通道控制方法来实现姿态稳定和机动控制。为研究导弹滚转自激失稳和闭环控制俯仰机动运动之间的相互影响过程，采用仅针对俯仰和偏航通道的两通道闭环控制方式来实现该机动过程，即根据当前反馈的迎角和角速度，结合给定的迎角指令，计算并给出俯仰舵偏指令，并根据当前弹体滚转角，将俯仰舵偏分解到4片尾舵上。图8为迎角闭环控制律原理框图。图中：αc为迎角指令；α为实时迎角响应；ωz为俯仰角速度；K1、K2和K3为各控制环节的增益参数。

图8　迎角闭环控制原理框图Fig.8　Principle schematic of angle of attack closed-loop control

试验过程中，先将模型的俯仰和滚转方向用电磁离合器锁定，风洞流场建立后，释放离合器，随后开始给定迎角指令，舵控仿真系统根据气动/运动参数测试系统测量得到的姿态角和角速度等参数计算舵偏指令，并传送到舵机，从而实现闭环控制。

图9为试验得到的导弹模型姿态角和舵偏角随时间的变化历程。结果显示，模型俯仰拉起过程中，出现俯仰/滚转耦合运动，使得闭环控制无法实现，原因为：在闭环控制过程中，滚转角发生变化，分解到俯仰和偏航通道的姿态角指令就会随着滚转角的变化而变化，大幅度滚转运动必将带来各通道姿态角指令的显著交替变化，从而使控制系统的响应特性变差，造成闭环控制失败。

图9　纵向两通道闭环控制试验结果Fig.9　Test results of longitudinal 2-channel closed-loop control

图10为对应状态的数值计算结果。与试验结果类似，当俯仰角拉起到指令值附近时，滚转方向迅速偏离平衡位置并发生连续振荡，弹体俯仰和偏航两个通道的舵偏角互相转换，对纵向的控制效果产生较大影响，产生较大幅度的俯仰振荡。

图10　纵向两通道闭环控制计算结果Fig.10　Numerical results of longitudinal 2-channel closed-loop control

虽然数值计算得到了与试验类似的滚转失稳和俯仰/滚转耦合运动，但具体的运动规律仍存在一定差异。

首先，计算得到的滚转失稳时机要晚于试验结果，滚转角在俯仰角达到指令目标附近才开始变化，而试验结果显示滚转失稳发生在拉起过程中。其主要和流场扰动情况有关，风洞试验状态下导弹受到流场、洞壁、支架和结构振动等多种影响，能够更快速地诱发失稳；而数值计算中几乎不存在非对称扰动，同时也未对洞壁和支架等进行模拟，失稳仅由网格非对称和数值误差等缓慢诱发。

其次，试验中导弹失稳后进入的耦合运动表现更为“规律”，俯仰角在25° 附近变化，滚转振荡振幅约为35°；而计算结果显示俯仰振荡发生在25° 以内，且俯仰和滚转姿态角的变化随机性较大。这是由于试验中的硬件条件接近真实飞行状态，舵偏角可以达到30° 以上，弹体滚转偏离时仍能够提供足够的控制力矩；而计算考虑到网格质量变化，将舵偏角限制在±12.5° 范围内，滚转角增大到一定程度后，尾舵产生的控制力矩不足，造成俯仰角显著偏小，俯仰角的大幅变化进一步导致了滚转气动特性的剧烈变化，从而产生更为复杂的耦合运动。

此外，数值计算采用的非定常雷诺平均Navier-Stokes(URANS)方法和S-A湍流模型并不能准确模拟真实的分离涡系发展、变化和相互干扰过程，在一定程度上也导致了计算和试验结果存在差异。

由图9和图10可以看到，导弹滚转运动对迎角闭环控制影响很大，容易导致闭环控制无法实现，甚至姿态失控。同时，如果滚转振荡的幅度太大，使得分解到各通道的舵偏角过大，从而导致舵效降低或反效，甚至到达实际舵偏角限制，会进一步降低姿态角的响应特性，大大增加飞行失控的可能性。要实现闭环控制，必须使分解到俯仰和偏航通道的姿态角指令值保持不变，即必须要求滚转姿态角始终保持在“×”字型状态。

4.3基于滚转优先控制的解耦控制方法

在4.2节的基础上，对弹体滚转通道实施控制，即采用三通道解耦控制方法来实现设定的机动过程。图11为滚转通道的控制框图，图中：γc为滚转角指令；γ为实时滚转角响应；ωx为滚转角速度；KGI、KGA和IX为各控制环节的增益参数。

图11　滚转通道闭环控制原理框图Fig.11　Principle schematic of roll closed-loop control theory

图12为三通道解耦控制的风洞试验结果。可以看出，导弹俯仰运动过程中，在滚转闭环控制的作用下，滚转角始终被保持在较小范围内，俯仰姿态能够保持稳定。图13为对应的计算结果。可以看到，计算与试验结果基本一致，控制系统能有效抑制滚转的进一步失稳。同时，由于数值计算的流场几乎不存在扰动，得到的控制效果更好。

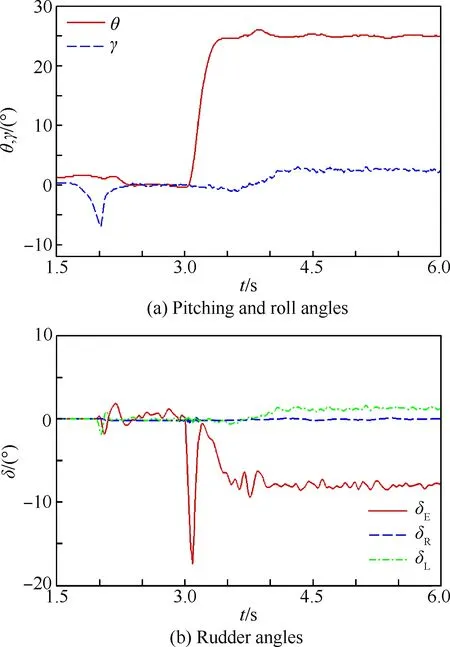
图12　三通道解耦闭环控制试验结果Fig.12　Test results of 3-channel decoupled closed-loop control

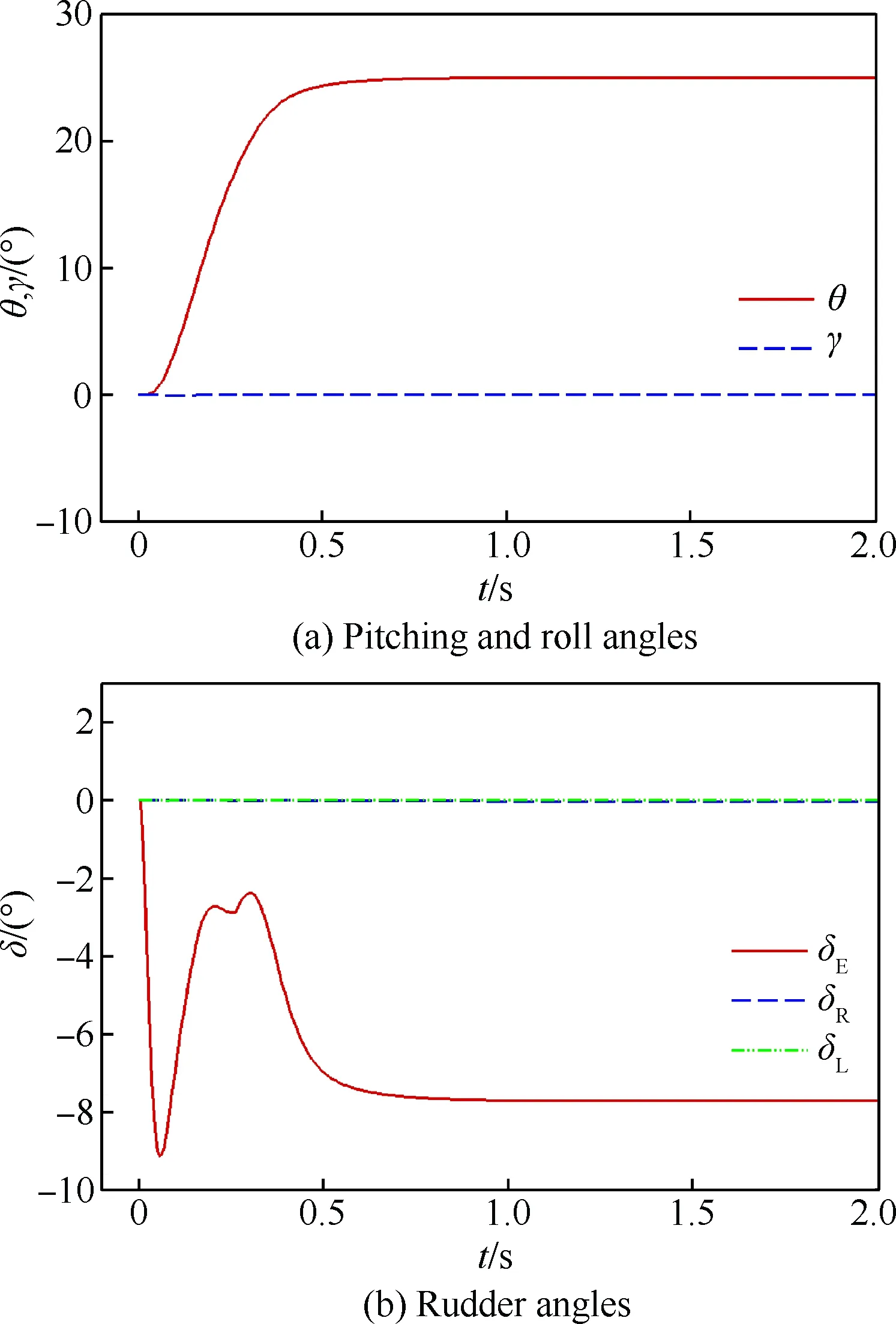
图13　三通道解耦闭环控制计算结果Fig. 13　Numerical results of 3-channel decoupled closed-loop control

因此，采用三通道解耦控制方法，能够在导弹俯仰机动过程中实现对滚转运动的有效抑制，使俯仰角能够快速达到并保持在指令点，从而实现俯仰和滚转运动的解耦控制。

5　结　论

为研究窄条翼导弹俯仰机动中的非指令自激滚转失稳的产生及对后续运动的影响过程，针对典型俯仰机动过程，开展了风洞试验和数值模拟研究，预测了导弹在俯仰机动过程中出现的滚转失稳及由此引起的多自由度耦合运动，并验证了三通道解耦控制方法的有效性。

1) 若不对滚转进行控制，导弹在俯仰机动过程中可能出现滚转方向的失稳和连续振荡，从而使得姿态角的响应特性变差，导致闭环控制失败，飞行姿态失控。

2) 同时对俯仰、偏航和滚转通道进行控制的三通道解耦控制方法能够有效抑制导弹的滚转失稳，改善闭环控制效果，保证姿态可控。

3) 采用的风洞虚拟飞行试验技术和数值虚拟飞行技术，能够初步实现典型高机动导弹的机动过程模拟，从而使在试飞前进行控制系统的有效验证成为可能。

[1]ALLEN J M. Aerodynamics of an axisymmetric missile concept having cruciform strakes and in-line tail fins from Mach 0.60 to 4.63: NASA/TM-2005-213541[R]. Washington, D.C.: NASA, 2005.

[2]达兴亚, 赵忠良, 陶洋. 窄条翼导弹模型摇滚特性试验研究[J]. 实验流体力学, 2012, 26(6): 40-43.

DA X Y, ZHAO Z L, TAO Y. Experimental investigation on free-to-roll motion of strake missile[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(6): 40-43 (in Chinese).

[3]RATLIFF C L, MARQUART E J. Bridging the gap between ground and flight tests: Virtual flight testing (VFT): AIAA-1995-3875[R]. Reston: AIAA, 1995.

[4]RATLIFF C L, MARQUART E J. An assessment of a potential test technique: Virtual flight testing (VFT): AIAA-1995-3415[R]. Reston: AIAA, 1995.

[5]GEBERT G, KELLY J, LOPEZ J. Wind tunnel based virtual flight testing: AIAA-2000-0829[R]. Reston: AIAA, 2000.

[6]PATTINSON J, LOWENBERG M H. A multi-degree-of-freedom rig for the wind tunnel determination of dynamic data[C]//AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 2009.

[7]杨小亮. 飞行器多自由度耦合摇滚运动数值模拟研究[D]. 长沙: 国防科学技术大学, 2012: 17-21.

YANG X L. Numerical investigation of aircraft rock in multiple degrees of freedom[D]. Changsha: National University of Defense Technology, 2012: 17-21 (in Chinese).

[8]赵忠良, 吴军强, 李浩, 等. 2.4 m跨声速风洞虚拟飞行试验技术研究[J]. 航空学报, 2016, 37(2): 504-512.

ZHAO Z L, WU J Q, LI H, et al. Investigations of virtual flight testing technique based on 2.4 m transonic wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 504-512 (in Chinese).

[9]李浩, 赵忠良, 陶洋. 风洞虚拟飞行试验模拟方法研究[J]. 实验流体力学, 2011, 25(6): 72-76.

LI H, ZHAO Z L, TAO Y. Simulation method for wind tunnel based virtual flight testing[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(6): 72-76 (in Chinese).

[10]阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社， 2006: 18-25.

YAN C. The methodology and application of computational fluid dynamics[M]. Beijing: Beihang University Press, 2006: 18-25 (in Chinese).

[11]SCHULTE A, EINARSSON G, RAICHLE A, et al. Numerical simulation of maneuvering aircraft by aerodynamic, flight mechanics and structural mechanics coupling: AIAA-2007-1070[R]. Reston: AIAA, 2007.

[12]SCHWARZ T. RANS simulations with one and six degrees of freedom rigid body motions[J]. New Results in Numerical and Experimental Fluid Mechanics VI, 2007, 96: 176-185.

[13]ALLAN M R, BADCOCK K J, RICHARDS B E. Numerical CFD based simulation of longitudinal flight mechanics with control[C]//Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2005.

[14]JOHN P D, JAMES D C, DAVID J B, et al. High resolution CFD simulation of maneuvering aircraft using the CREATE-AV/Kestrel solver: AIAA-2011-1109[R]. Reston: AIAA, 2011.

[15]DAVID R M, DAVID R S, TODD R T, et al. Aerodynamic control surface implementation in Kestrel v2.0: AIAA-2011-1175[R]. Reston: AIAA, 2011.

[16]SCOTT A M, TIMOTHY A E, STEVEN L, et al. Relative motion simulation using an overset multimesh paradigm with Kestrel v3: AIAA-2012-0712[R]. Reston: AIAA, 2012.

[17]SAHU J, HEAVEY K R. Parallel CFD computations of projectile aerodynamics with a flow control mechanism [J]. Computers & Fluids, 2013, 88(12): 678-687.

[18]陶洋, 范召林, 吴继飞. 基于CFD的方形截面导弹纵向虚拟飞行模拟[J]. 力学学报, 2010, 42(2): 169-176.

TAO Y, FAN Z L, WU J F. CFD based virtual flight simulation of square crosssection missile with control in longitudinal flight[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(2): 169-176 (in Chinese).

[19]达兴亚, 陶洋, 赵忠良. 基于预估校正和嵌套网格的虚拟飞行数值模拟[J]. 航空学报, 2012, 33(6): 977-983.

DA X Y, TAO Y, ZHAO Z L. Numerical simulation of virtual flight based on prediction-correction coupling method and chimera grid[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(6): 977-983 (in Chinese).

[20]席柯, 袁武, 阎超, 等. 基于闭环控制的带翼导弹虚拟飞行数值模拟[J]. 航空学报, 2014, 35(3): 634-642.

XI K, YUAN W, YAN C, et al. CFD based virtual flight simulation of the basic finner projectile with closed loop[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 634-642 (in Chinese).

王晓冰男， 硕士， 助理工程师。主要研究方向： 非定常空气动力学。

Tel.: 0816-2462544

E-mail: wangxbice@163.com

赵忠良男， 硕士， 研究员， 硕士生导师。主要研究方向： 非定常空气动力学。

Tel.: 0816-2462109

E-mail: zzzhao_cardc@sina.com

Roll instability and control during pitching maneuver fora missile with strake wings

WANG Xiaobing, ZHAO Zhongliang*, LI Hao, DA Xingya, TAO Yang

High Speed Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang621000, China

The aerodynamic characteristics in roll of the missile with strake wings are always complicated, which can easily cause the non-directive deviation and oscillation and may lead to losing control of flight and impairing target accuracy. Investigations using the virtual flight testing system in 2.4 m transonic wind tunnel are conducted to study the interplay of roll instability and the longitudinal closed-loop control, and numerical simulation is also performed using the integrative method by aerodynamic/motion/control coupling. The results show that both wind tunnel test and numerical simulation predict the non-directive rolling motion and the pitch/roll coupled motion and prove that the decoupled control method can effectively inhibit the rolling motion and maintain a steady flight.

missile with strake wings; roll instability; virtual flight; wind tunnel test; numerical simulation; closed-loop control

2016-02-16； Revised： 2016-02-17； Accepted： 2016-03-28； Published online： 2016-04-1316:00

s： National Natural Science Foundation of China (91216203, 11372336， 11532016)

. Tel.： 0816-2462109E-mail: zzzhao_cardc@sina.com

2016-02-16； 退修日期： 2016-02-17； 录用日期： 2016-03-28；

时间： 2016-04-1316:00

www.cnki.net/kcms/detail/11.1929.V.20160413.1600.008.html

国家自然科学基金 (91216203, 11372336， 11532016)

.Tel.： 0816-2462109E-mail: zzzhao_cardc@sina.com

10.7527/S1000-6893.2016.0101

V211.7

A

1000-6893(2016)08-2517-08

引用格式： 王晓冰， 赵忠良， 李浩， 等． 窄条翼导弹俯仰机动中滚转失稳及其控制过程[J]． 航空学报, 2016, 37(8): 2517-2524. WANG X B, ZHAO Z L, LI H, et al. Roll instability and control during pitching maneuver for a missile with strake wings[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2517-2524.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160413.1600.008.html