基于拉格朗日拟序结构的局部激励流动分离控制有效性分析方法

康伟， 张权麒， 代向艳， 刘磊

1.西北工业大学 航天学院， 西安　710072 2.空军工程大学 航空航天工程学院 等离子体动力学重点实验室， 西安　710038



基于拉格朗日拟序结构的局部激励流动分离控制有效性分析方法

康伟1,*， 张权麒1， 代向艳2， 刘磊1

1.西北工业大学 航天学院， 西安710072 2.空军工程大学 航空航天工程学院 等离子体动力学重点实验室， 西安710038

从流体输运角度提出了用于局部周期激励流动分离控制有效性研究的数值分析方法。基于有限时间不变流形理论建立用于非定常流动的流体输运分析方法, 并采用数值方法从非定常流场中提取得到吸引拉格朗日拟序结构(LCSs)和排斥LCSs描述流体输运行为。通过对局部周期激励的流动分离控制规律的研究，结果表明存在三种与激励频率相关的影响翼型气动特性的流体输运模式，其中在锁频激励下吸引LCSs在前缘形成的尖楔结构有效增强主流与分离区流体的物质交换，减小翼面流动分离区的面积，显著提高翼型升力。

流动分离； 流动控制； 锁频； 流体输运； 拉格朗日拟序结构； 增升

流动分离是影响翼型性能的重要流动现象之一。流动分离控制与分析对提高翼型的气动性能有着重要的意义[1-3]。目前，对流动分离的描述主要采用Prandtl的分离准则[4]。但是，对于非定常流动，该方法能够从欧拉角度描述某一瞬时流动分离特征，但无法有效刻画非定常流动分离的时间关联性，也不能对分离结构的动力学特性进行有效分析。

从拉格朗日角度来看，流动分离在本质上是一种流体输运现象，即流体质点从壁面附近进入到流体内部的动力学过程。为了建立流体中输运边界的描述方法，Haller和Yuan[5]于2000年基于有限时间稳定流形和不稳定流形提出了拉格朗日拟序结构(LCSs)。进一步地，通过对不同时刻对应输运边界的稳定流形与不稳定流形之间的相交面(缠绕)，来分析主流与分离区之间流体的输运变化。2006年Shadden等[6]应用该方法研究水母在自由移动时产生的涡环尾流中的物质输运作用，并与已有的欧拉描述方法进行了对比，发现对于非定常流动在拉格朗日坐标系下对输运边界的识别优于欧拉描述方法。2011年Haller[7]重新定义了LCSs的数学方法，即沿着稳定流形方向运动的物线中最短的即为有限时间稳定流形，其附近任何其他物线将由于稳定流形的排斥作用在其法线方向被拉伸。目前，LCSs已被应用于多个领域内流动现象的研究中，如Mathur等[8]研究了湍流中的拉格朗日结构，Beron-Vera等[9]对采用LCSs描述了海洋流动中大尺度涡系之间的作用关系，Lipinski等[10]将LCSs应用于二维翼型绕流中的涡脱落过程，国内的杨岸龙等[11]采用LCSs研究了圆盘启动过程的流体输运规律。雷鹏飞等[12]采用LCSs对圆柱绕流的瞬态起动过程的动力学行为进行了分析。

本文基于LCSs建立流动分离控制规律的分析方法，旨在研究控制激励对非定常流动分离及流动输运的影响规律，探索其流动分离控制机理，为飞行器气动设计与流动控制提供重要的理论参考依据。

1　流体输运的描述方法

1.1拉格朗日拟序结构概述

从动力学的角度来看，流体微团在流动中会发生拉伸与压缩的现象，而这些现象与动力系统中双曲奇点的稳定流形与不稳定流形密切相关：沿稳定流形被压缩、沿不稳定流形被拉伸。基于这个思路，Haller和Yuan[5]针对非定常流动提出了有限时间稳定与不稳定流形，用于描述非定常流动、甚至湍流中的动力学行为。这些有限时间稳定与不稳定流形构成了LCSs。而有限时间稳定和不稳定流形可以由有限时间李雅普诺夫指数(Finite-Time Lyapunov Exponent，FTLE)来描述在有限时间内的局部最大排斥和吸引度的迹线，即流体质点与附近流体的距离在有限时间内变化的程度。

对于定常和周期流动中稳定与不稳定流形所描述的流动结构也可以看做是LCSs。

1.2拉格朗日拟序结构的计算方法

对于非定常流动，无量纲t0时刻x处的流体质点可以通过迹线的定义式计算得到在t1时刻的流动速度。通过数值积分的方法即可得到x处流体质点的新位置，记为映射形式：

(1)

则t0时刻到t1时刻该流体质点的李雅普诺夫指数可以由式(2)计算得到：

(2)

通过计算流场中每一点(离散后)的FTLE场，即可得到流场中的FTLE分布。由Shadden等推导[13]可知，FTLE场中的等势脊线对应流场中的LCSs。

采用中心差分来逼近式(2)中的导数。从计算所得的FTLE分布可以看到，当FTLE趋近于恒定时，所得的LCSs结构能够精确描述非定常流动分离等流动特征结构。更重要的是不同时刻LCSs中稳定流形和不稳定流形之间产生的缠绕所形成的区域(Lobes)[9]的面积及其演化过程能够反映不同流动区域之间的流体输运规律。

需要指出的是由于该方法是从非定常流场中的速度分布中提取得到FTLE场，进而得到LCSs。因此，该方法可以利用已有计算/试验结果得到的流场数据来提取流场的流动特性，以达到分析流动特征的目的。因此，该方法的可靠性取决于计算或试验结果的精度和准确性。若采用计算流体力学(CFD)或试验方法所得的流场结果真实可信，则该方法即可用于所得流场结果的特征提取与分析中。

2　局部周期激励的流动控制动力学模型

2.1局部激励模型

激励是采用外部能源供应引起翼面局部结构变形的流动控制方式，例如压电薄膜激励，柔性膜强迫振动激励等。其物理本质是翼面局部以某一频率进行等幅振动，引起流场扰动，进而改变流动状态，达到流动控制的目的。参考文献[14]对周期激励位置与激励区大小进行的总结，在沿弦向近上翼面前缘[0，0.1]处施加周期性的简谐振动。图1给出了局部周期激励的示意图。局部周期激励表示为

(3)

以翼型弦长c和自由来流速度U∞进行无量纲化，则式(3)变为

(4)

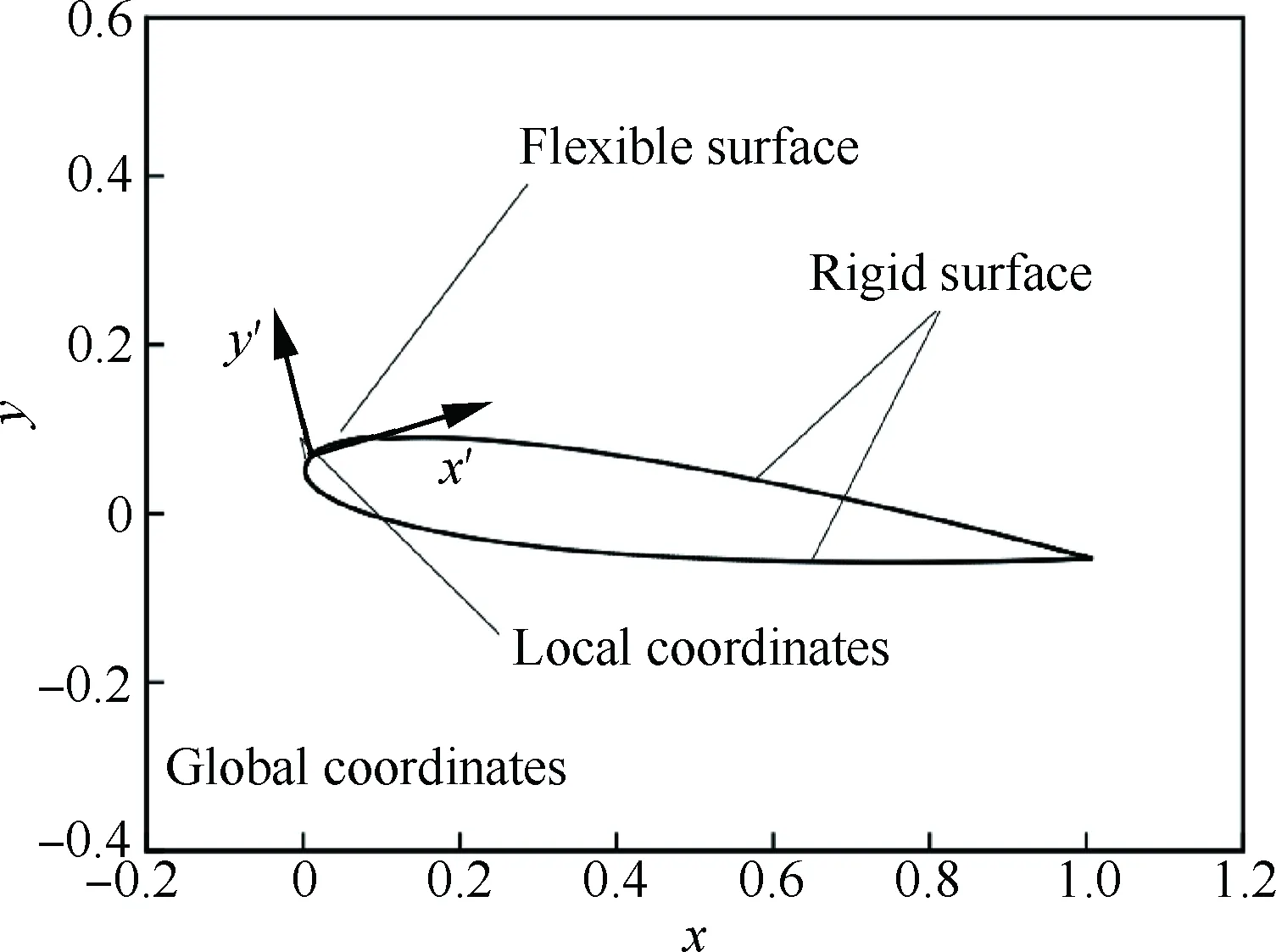
图1　局部周期激励示意图Fig.1　Schematic of local periodic actuation

2.2非定常流动的数值方法

针对二维非定常黏性不可压流动，采用基于特征线有限元方法[15-17]求解非定常黏性流动控制方程。该算法的具体推导可参考文献[2-3,18]，其中空间离散采用线性形函数的三角形单元，时间离散采用欧拉方法。动网格技术采用弹簧近似方法[19-20]。

图2比较了雷诺数Re=100时静止流体中振动圆柱的阻力系数CD，可以看出所提方法的计算结果与文献结果[21]吻合良好。

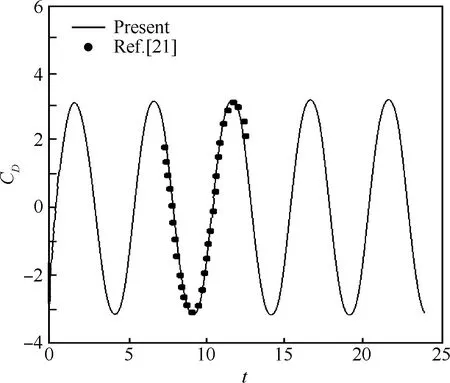
图2　Re=100时静止流体中振动圆柱的阻力系数比较Fig.2　Comparison of drag coefficients for oscillating circular cylinder in water at rest at Re=100

3　结果分析

前期工作[1-3,18,22]已发现局部周期激励对翼型升力具有增升效果，特别是流动特征频率锁定于激励频率时，翼型升力提高显著。在本文中，fref的选取参考了作者采用局部柔性翼面自激振动得到最佳增升效果时对应的结构基频为参考频率[3]。如图3所示，迎角为6° 时，周期锁频激励的増升ΔCL高达67%，但即使发生锁频，増升效果也有显著不同[3]。

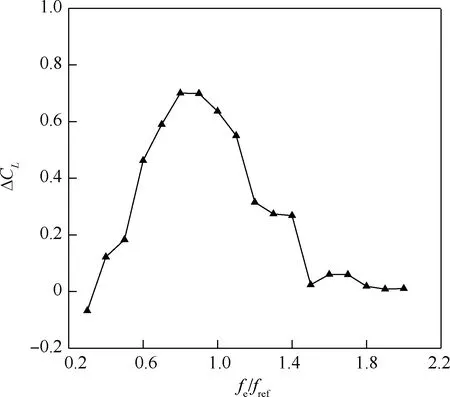
图3　Re=5 000时不同激励频率下翼型升力系数的变化曲线[3]Fig.3　Variation of lift coefficients of airfoil with differentactuating frequencies at Re=5 000

本文采用所提方法选取Re=5 000,迎角为6° 时的四种典型激励情况分析输运特性与增升的关系，用于流动分离控制的规律分析。

3.1流体输运分析

3.1.1刚性翼型的流体输运特征

对于刚性翼型绕流，翼型附近的流动区域被吸引LCSs分为主流和流动分离区两部分，如图4(a)所示。在一个周期内，翼型上表面附近的LCSs随时间几乎保持定常状态，说明翼型上表面附近大部分区域内流动分离区与主流的流体之间不存在物质交换，在分离点下游形成大范围流动死区。从图5(a)可以看出流动死区对应的压力分布相对较为平缓，对升力的贡献起到消极影响。

在翼型后缘及尾迹内，吸引LCSs与排斥LCSs相互缠绕形成的区域反映了主流与分离区域之间出现了物质交换作用，如图4(a)中分离泡内区域沿着拉伸的LCSs逐渐向尾迹移动，最终形成具有负涡量的旋涡；主流内区域的流体沿着LCSs逐渐向分离区内部移动，但其移动范围仅限于靠近翼型后缘的分离区域，分离点附近的流动死区则不受其影响。

3.1.2低频激励时翼型的流体输运特征

当fe=0.5fref时，非定常流动过程与刚性翼型绕流相似。较刚性翼型情况，在激励的作用下，流体从主流到分离区的输运提前发生。主流内流体在翼型中后部沿着LCSs向分离区内部移动，使得主流流体被输运到分离泡内，如图4(b)所示。

由伯努利方程可知旋涡附近的壁面压力迅速减小。然而，由于激励频率较低，旋涡脱落周期长。当旋涡脱落后，翼型尾部上表面压力迅速增大，甚至大于翼型下表面压力，出现负的压差，使翼型升力急剧下降(见图5(b) t=3T/4)。因此，fe=0.5fref时的增升效果较弱。

3.1.3锁频激励时翼型的流体输运特征

当fe=0.9fref时，由于锁频激励的作用，吸引LCSs在上翼面前缘处形成尖楔结构(见图5(c) t = 0时前缘附近)。这种尖楔结构是由Van

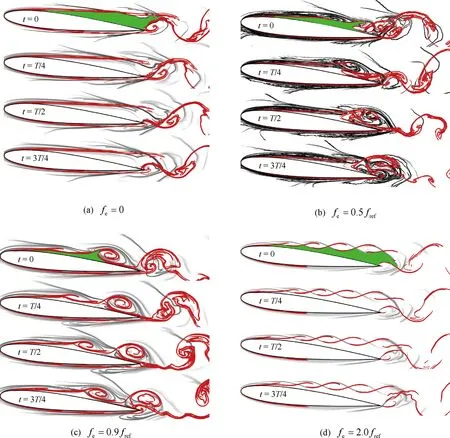
图4　Re=5 000时一个周期T内四种典型激励频率下的流场拉格朗日拟序结构(LCSs)图(红色实线：吸引LCSs；黑色脊线：排斥LCSs)　Fig.4　Lagrangian coherent structures (LCSs) near the airfoil under four typical actuating frequencies at Re=5 000 (Red line: Attracting LCSs; Black ridge: Repelling LCSs)

图5　一个周期T内四种典型激励频率下的翼面压力分布图Fig.5　Pressure distribution on the airfoil under four typical actuating frequencies in a period T

Dommelen和Cowley[23]在流动分离的拉格朗日描述中首次发现的。尖楔结构的形成如图6所示[24]，初始平行于壁面的质点随时间沿着分离流线逐渐向流体内部输运，最终形成一尖锐突起。

图6　定常流动分离中尖楔结构的形成过程[24](蓝色线：尖楔结构；黑色线：流线)Fig.6　Formation of material spike in steady flow separation[24] (Blue line： Material spike;Black line：Streamline)

如图6所示定常流动中分离流线与尖楔结构相互重合，该结果验证了所提描述方法的可靠性。而在非定常流动中，流线无法有效描述流体质点的非定常流动分离动力学特性。而由于尖楔结构建立于拉格朗日坐标系，因此它能够描述流体质点的非定常流动分离特性。

从图4(c)中可以看出尖楔结构以一定周期向下游拉伸，并向翼面折叠，将主流的高动能流体迅速向壁面附近输运。随着尖楔结构向下游移动的过程中，排斥LCSs和吸引LCSs相互缠绕，表明流体从主流向分离区输运，大幅提高了壁面附近流体的动能，减小了流动死区面积(对比图4中的绿色阴影区域面积)。从压力云图5(c)中也可以看到分离泡内部保持着较低的压力分布，因而翼型升力显著提高。

3.1.4高频非锁频激励时翼型的流体输运特征

当fe=2.0fref时，在翼面上表面虽然也产生了尖楔结构，但是排斥LCSs与吸引LCSs几乎重合，并向远离翼面方向发展。这表明主流流体不再向流动分离区内部输运，导致流体无法将足够的动能传递到边界层内。相应地，在翼面后缘区形成了较大范围的死水区(如图4(d)中的绿色阴影区域面积)。如图5(d)所示，翼型上表面压力降低效果减弱，无法有效提高翼型升力。

3.2流动分离控制规律分析

从不同激励频率下流体输运规律可以看出，激励作用存在不同的流动模式，模式A：锁频激励时，尖楔结构在前缘产生，向下游拉伸并向翼面折叠，这使得翼面的LCSs结构在前缘附近发生缠绕，促进主流与分离区的流动输运作用，此时增升效果良好。模式B：低频激励时，翼面LCSs结构只在后缘附近发生缠绕，由于位置接近后缘，不利于主流与翼面分离区的流体输运，此时增升效果差。模式C：高频非锁频激励时，翼面的吸引LCSs与排斥LCSs重合，无法从主流向分离区进行流体输运，这时増升效果差。

4　结　论

1) 文中所提的流体输运分析方法能够用于流动分离控制的有效性分析, 为飞行器气动设计与流动控制提供理论指导与参考依据。

2) 从非定常流动中提取的吸引LCSs与排斥LCSs的缠绕与折叠反映了翼型主流与流动分离区的流体输运情况。

3) 锁频激励能够有效增强主流与分离区流体输运作用。这时，翼面流动分离区的面积最小，翼型上表面压力降低。

4) 通过对流场LCSs的分析可知，激励频率相关的影响翼型气动特性的流体输运模式可以分为三类：① 锁频激励时，前缘产生的尖楔结构能够使得翼面的LCSs结构在前缘附近发生缠绕，促进主流与分离区的流动输运作用；② 低频激励时，翼面LCSs结构只在后缘附近发生缠绕，不利于主流与翼面分离区的流体输运;③ 高频非锁频激励时，翼面的吸引LCSs与排斥LCSs重合，无法从主流向分离区进行流体输运。

下一步将应用所提方法对机翼绕流的三维流动分离特征进行研究。

[1]KANG W, LEI P F, ZHANG J Z, et al. Effects of local oscillation of airfoil surface on lift enhancement at low Reynolds number[J]. Journal of Fluids and Structures, 2015, 57: 49-65.

[2]KANG W, ZHANG J Z, FENG P H. Aerodynamic analysis of a localized flexible airfoil at low Reynolds numbers[J]. Communications in Computational Physics, 2012, 11(4): 1300-1310.

[3]KANG W, ZHANG J Z, LEI P F, et al. Computation of unsteady viscous flow around a locally flexible airfoil at low Reynolds number[J]. Journal of Fluids and Structures, 2014, 46: 42-58.

[4]FOX R W, MCDONALD A T, PRITCHARD P J. Introduction to fluid mechanics[M]. New York: John Wiley & Sons 1985: 408-423.

[5]HALLER G, YUAN G. Lagrangian coherent structures and mixing in two-dimensional turbulence[J]. Physica D: Nonlinear Phenomena, 2000, 147(3): 352-370.

[6]SHADDEN S C, DABIRI J O, MARSDEN J E. Lagrangian analysis of fluid transport in empirical vortex ring flows[J]. Physics of Fluids, 2006, 18(4): 047105.

[7]HALLER G. A variational theory of hyperbolic lagrangian coherent structures[J]. Physica D: Nonlinear Phenomena, 2011, 240(7): 574-598.

[8]MATHUR M, HALLER G, PEACOCK T, et al. Uncovering the Lagrangian skeleton of turbulence[J]. Physical Review Letters, 2007, 98(14): 144502.

[9]Beron-Vera F J, OLASCOAGA M J, GONI G J. Oceanic mesoscale eddies as revealed by Lagrangian coherent structures[J]. Geophysical Research Letters, 2008, 35(12): L12603.

[10]LIPINSKI D, CARDWELL B, MOHSENI K. A Lagrangian analysis of a two-dimensional airfoil with vortex shedding[J]. Journal of Physics A: Mathematical and Theoretical, 2008, 41(3-4): 344011.

[11]杨岸龙, 贾来兵, 尹协振. 用拉格朗日相关结构研究圆盘启动过程的流体输运[J]. 实验力学, 2012, 27(6): 677-683.

YANG A L, JIA L B, YIN X Z. On the fluid transport in disk starting process by lagrangian coherent structures[J]. Journal of Experimental Mechanics, 2012, 27(6): 677-683 (in Chinese).

[12]雷鹏飞, 张家忠, 王琢璞, 等. 非定常瞬态流动过程中的Lagrangian拟序结构与物质输运作用[J]. 物理学报, 2014, 63(8): 84702-084702.

LEI P F,ZHANG J Z,WANG Z P, et al. Lagrangian coherent structure and transport in unsteady transient flow[J]. Acta Physica Sinica, 2014, 63(8): 084702 (in Chinese).

[13]SHADDEN S C, LEKIEN F, MARSDEN J E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows[J]. Physica D: Nonlinear Phenomena, 2005, 212(3): 271-304.

[14]GURSUL I, CLEAVER D, WANG Z. Control of low reynolds number flows by means of fluid-structure interactions[J]. Progress in Aerospace Sciences, 2014, 64: 17-55.

[15]KANG W, ZHANG J Z, REN S, et al. Nonlinear galerkin method for low-dimensional modeling of fluid dynamic system using POD modes[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22(1): 943-952.

[16]ZIENKIEWICZ O C, CODINA R. A general algorithm for compressible and incompressible-flow.1. the split, characteristic-based scheme[J]. International Journal for Numerical Methods in Fluids, 1995, 20(8-9): 869-885.

[17]ZIENKIEWICZ O C, MORGAN K, SAI BVKS, et al. A general algorithm for compressible and incompressible-flow.2. tests on the explicit form[J]. International Journal for Numerical Methods in Fluids, 1995, 20(8-9): 887-913.

[18]康伟, 张家忠. 翼型局部弹性自激振动的增升减阻效应研究[J]. 西安交通大学学报, 2011, 45(5): 94-101.

KANG W, ZHANG J Z. Numerical analysis of lift enhancement and drag reduction by self-induced vibration of localized elastic airfoil[J]. Journal of Xi’an Jiaotong University, 2011, 45(5): 94-101 (in Chinese).

[19]BATINA J T. Unsteady euler algorithm with unstructured dynamic mesh for complex-aircraft aerodynamic analysis[J]. AIAA Journal, 1991, 29(3): 327-333.

[20]BLOM F J. Considerations on the spring analogy[J]. International Journal for Numerical Methods in Fluids, 2000, 32(6): 647-668.

[21]DÜTSCH H, DURST F, BECKER S, et al. Low-Reynolds-number flow around an oscillating circular cylinder at low Keulegan-Carpenter numbers[J]. Journal of Fluid Mechanics, 1998, 360: 249-271.

[22]康伟, 刘磊, 徐敏, 等. 低雷诺数下翼面局部振动增升机理研究[J]. 航空学报, 2015, 36(11): 3557-3566.

KANG W, LKU L, XU M, et al. Lift enhancement mechanism for local oscillation of airfoil surface at low Reynolds number[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(11): 3557-3566 (in Chinese).

[23]VAN DOMMELEN L L, COWLEY S J. On the Lagrangian description of unsteady boundary layer separation, part 1. general theory[J]. Journal of Fluid Mechanics, 1990, 210(-1): 593-626.

[24]HALLER G. Exact theory of unsteady separation for two-dimensional flows[J]. Journal of Fluid Mechanics, 2005, 512(10): 257-311.

康伟男， 博士， 讲师。主要研究方向： 气动弹性与流动控制。

Tel.: 029-88494614

E-mail: wkang@nwpu.edu.cn

张权麒男， 大学本科生。主要研究方向： 流动控制。

Tel.: 029-88494614

E-mail: wkang@nwpu.edu.cn

代向艳女， 博士研究生。主要研究方向： 气动弹性与流动控制。

Tel.: 029-88494614

E-mail: daixiangyan302@163.com

刘磊男， 硕士研究生。主要研究方向： 气动伺服弹性。

Tel.: 029-88494614

E-mail: wkang@nwpu.edu.cn

A method for effectiveness analysis of flow separation control bylocal actuation based on Lagrangian coherent structures

KANG Wei1，*， ZHANG Quanqi1， DAI Xiangyan2， LIU Lei1

1. School of Astronautics, Northwestern Polytechnical University, Xi’an710072, China 2. Science and Technology on Plasma Dynamics Laboratory, School of Aeronautics and Astronautics Engineering,Airforce Engineering University, Xi’an710038, China

A numerical method for the effectiveness analysis for the flow separation control by local periodic actuation is presented from the perspective of fluid transport. Finite time invariant manifold theory is used for the establishment for fluid transport analysis of unsteady flow. The attracting Lagrangian coherent structures (LCSs) and the repelling LCSs are extracted from the unsteady flow field using numerical method to describe the behaviors of fluid transport. Study on the flow separation control of local periodic excitation indicates that there exist three kinds of fluid transport mode with actuating frequency affecting the aerodynamic performance of the airfoil. In particular, as the actuation with lock-in frequency is activated, the material spike formed at the leading edge from the attracting LCSs effectively enhances the fluid exchange between mainstream and separation region, which reduces the area of separation zone, and significantly improves the airfoil lift.

flow separation; flow control; frequency lock-in; fluid transport; Lagrangian coherent structure; lift enhancement

2015-09-16； Revised： 2015-11-10； Accepted： 2015-12-30； Published online： 2016-01-2516：38

s： National Natural Science Foundation of China (11402212); the Fundamental Research Funds for the Central Universities (3102014JCQ01002)

. Tel.： 029-88494614E-mail: wkang@nwpu.edu.cn

2015-09-16； 退修日期： 2015-11-10； 录用日期： 2015-12-30；

时间： 2016-01-2516：38

www.cnki.net/kcms/detail/11.1929.V.20160125.1638.006.html

国家自然科学基金 (11402212)； 中央高校基本科研业务费专项资金 (3102014JCQ01002)

.Tel.： 029-88494614E-mail: wkang@nwpu.edu.cn

10.7527/S1000-6893.2015.0363

V211.3

A

1000-6893(2016)08-2490-08

引用格式： 康伟， 张权麒， 代向艳, 等． 基于拉格朗日拟序结构的局部激励流动分离控制有效性分析方法[J]． 航空学报, 2016, 37(8): 2490-2497. KANG W, ZHANG Q Q, DAI X Y, et al. A method for effectiveness analysis of flow separation control by local actuation based on Lagrangian coherent structures[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2490-2497.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160125.1638.006.html