基于数值虚拟飞行技术的飞行器动态特性分析

黄宇， 阎超,*， 席柯， 王文

1.北京航空航天大学 航空科学与工程学院， 北京　100083 2.中国兵器工业导航与控制技术研究所, 北京　100089



基于数值虚拟飞行技术的飞行器动态特性分析

黄宇1， 阎超1,*， 席柯2， 王文1

1.北京航空航天大学 航空科学与工程学院， 北京100083 2.中国兵器工业导航与控制技术研究所, 北京100089

基于结合结构重叠网格、闭环PID控制器、舵偏控制律、刚体六自由度运动和非定常Navier-Stokes方程求解等模块的数值虚拟飞行技术，对“起源号”返回舱、基本带翼导弹外形的多自由度非定常运动、受控特性及控制参数的整定开展了模拟。分析了不同自由度(DOF)下飞行器的运动特性，飞行器受扰动后的稳定性及控制参数的整定。计算结果表明：利用数值虚拟飞行技术可有效地开展复杂流动下飞行物体非线性运动问题的研究，对研究飞行器在非线性流动下的动态特性、受控特性、流动机理研究以及控制律的设计检验具有较高的工程价值和应用前景。

计算流体力学(CFD)； 重叠网格； PID控制； 虚拟飞行； 动导数； 控制参数整定； 动态特性； 非定常流动

飞行器在大迎角、过失速等状态下飞行时，会出现复杂的分离涡等强非线性、非定常流动，与飞行器运动耦合将会使飞行器产生一系列的非定常运动现象，如极限环摇滚、俯仰振荡等，从而引起飞行器气动力的突变、迟滞及非对称特性，极易导致飞行器运动进入发散状态，严重影响飞行器的安定性、稳定性及受控性。由此，现代先进空战武器设计对飞行器的动态特性、稳定性及控制效率等的预测技术提出了要求[1]。

飞行器出现非定常、非线性流动情况下，线性化数据不能正确地刻画飞行器非线性的气动力和运动规律[2-3]。为了能有效地研究飞行器非定常运动中的气动、控制等问题，国内外研究人员从20世纪80年代开始发展了一种新型的风洞试验技术，即风洞虚拟飞行技术[4-6](Wind Tunnel Based Virtual Flight Testing)。通过将实验缩比模型安装有若干个自由度的支撑机构上，在风洞中开展运动模型的动力特性、控制特性的综合实验，在一定程度上模拟飞行器的真实飞行状态，获得飞行器动态品质及控制特性。但由于风洞试验的固有缺陷，如支架/洞壁干扰、机械阻尼、相似准则等难以完全满足等情况，导致难以准确地测量动态参数。此外，由于风洞一般只能提供直匀流，且模型支撑机构并不能在大范围内实现真实飞行自由度，因而模拟的仿真程度也受到制约。

近年来，计算流体力学(Computational Fluid Dynamics， CFD)及大规模高性能计算技术发展迅速，CFD在基础理论和工程实践上都取得了令人瞩目的成就，以CFD技术为基础实现的基于方程的数值虚拟飞行技术已经成为可能[7-8]。数值虚拟飞行技术将飞行动力学方程/流体力学方程/控制律耦合实时求解，可开展全尺寸，真实运动/气流参数的非定常模拟，避免了风洞虚拟飞行技术的固有缺点，运动仿真程度更高。此外数值虚拟飞行技术灵活性更好、耗费低、周期短，在机理研究中对流场、运动参数的获取更为方便和丰富，在实际工程应用中可在各个阶段介入研究，为设计及验证飞行器气动、控制等系统的特性提供有力的依据，填补风洞虚拟飞行及飞行试验的不足[9]。

本文基于数值虚拟飞行技术，开展了返回舱、带翼导弹外形的动态特性研究。研究结果表明：数值虚拟飞行技术对复杂运动下的飞行器动态特性、飞行器的操纵特性、控制系统参数的整定等问题的研究具有较高的工程价值和应用前景。

1　数值虚拟飞行方法

1.1流动主控方程

主控方程为非定常、可压缩、雷诺平均的三维Navier-Stokes方程。采用来流参数为无量纲特征变量，对方程无量纲化，并将方程转换到一般曲线坐标系下，可得如下形式[8]：

(1)

式中：Q为守恒变量向量；F、G和H为对流通量；Fv、Gv和Hv为黏性通量；Re为来流雷诺数。

采用基于结构网格的有限体积法求解，对流通量计算采用带熵修正的Roe格式，采用MUSCL插值和vanAlbada限制器达到二阶空间精度。时间推进格式在定常计算时选用隐式LU-SGS方法，在非定常计算时选用双时间步LU-SGS格式。采用一方程的Spalart-Allmaras湍流模型计算获得湍流涡黏性。利用基于共享内存的Open-MP并行技术加速计算。

1.2结构重叠网格技术

网格生成是数值模拟的重要部分之一，好的网格质量是获得合理计算结果的前提条件。结构重叠网格逻辑关系简单，鲁棒性好，适合开展工程计算。在大部分计算区域，结构重叠网格计算方法同结构网格完全一样，并能保证和结构网格相同的计算精度、计算效率及流动特性捕捉能力，而网格间的重叠技术降低了复杂拓扑外形的网格生成难度[10-12]。另一方面，虚拟模拟实际问题时，被模拟物体子部件间往往会出现相对运动，如舵面/襟翼等部件受控偏转、飞行器脱离挂架等，结构重叠网格将各子部件划为独立的子区域，可有效地处理这些多体运动、分离问题[12]。求解多体、部件运动等位置或形状随时间变化的问题时，网格无需重新生成，各子区域网格随部件作刚性运动，每一时间步只需要进行一次重叠过程以建立插值信息关系，相比网格重构、变形等动网格方法实现更为简单高效，且适用于任意幅度的运动[12-13]。

1.3飞行器刚体6DOF运动方程组

飞行器或运动部件作为刚体处理,在空间中刚体运动有6个自由度(DOF)，刚体在空间的平动、转动、位置及姿态的变化可以用6个动力学方程和6个运动学方程充分描述[14]。

刚体质心动力学方程为

(2)

式中:a和V分别为惯性系下加速度和速度矢量；P和F分别为推力和气动力在体轴坐标系下矢量，下标b表示体轴系；G为惯性系下重力矢量；L为坐标转换矩阵；m为质量。

惯性坐标系下质心运动学方程为

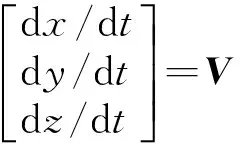
(3)

体轴坐标系下刚体绕质心转动的动力学方程为

(4)

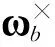
(5)

由式(4)可得体轴系下绕质心转动的动力学方程为

(6)

再结合体轴系下角速度分量同姿态角变化关系式(7)，可获得关于俯仰角θ、偏航角φ及滚转角γ的刚体动力学和运动学联立的方程组为

(7)

1.4控制系统模化

飞行控制系统一般由舵回路、稳定回路和制导回路这3个反馈回路构成。这3个回路主要实现气动力(气动面)控制、担负稳定与控制功能，以及按照一定导引律给出控制指令[15]。

在数值虚拟飞行中可以使用任意的控制器，复杂的控制器的实现、考察不在本文研究范围中。为简化起见，本文采用PID控制器，实现舵偏反馈控制，并形成稳定的制导回路来跟踪指定迎角变化规律。PID控制器如图1所示。

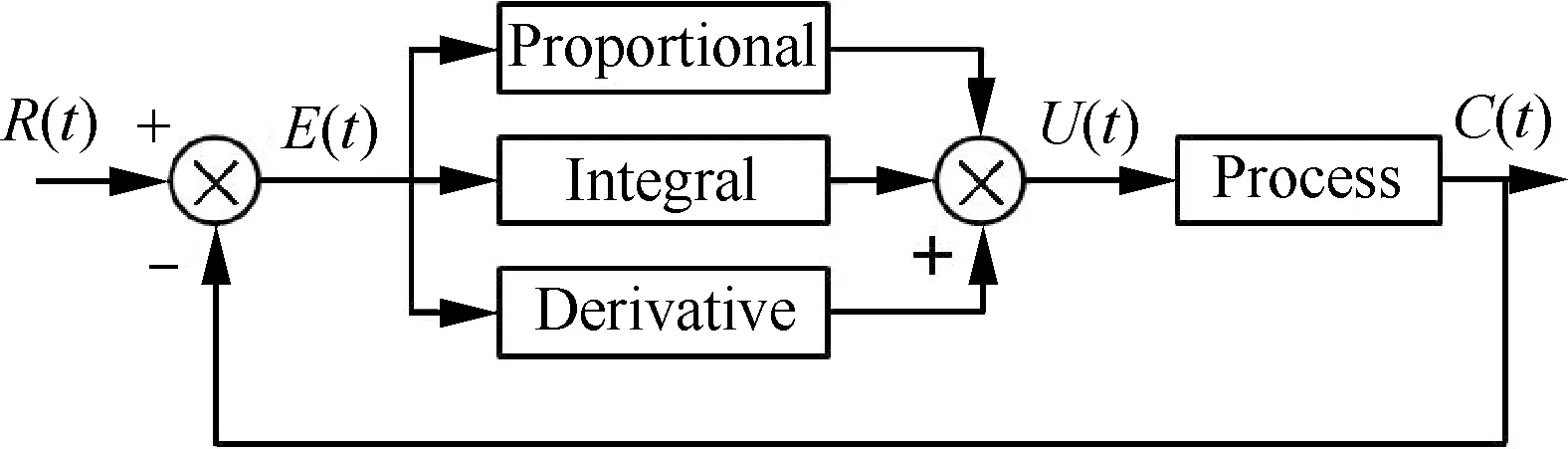
图1　PID控制器框图Fig.1　Block diagram of PID controller

图中：R(t)为设定值，C(t)为检测值，E(t)为设定值和检测值间的偏差，可见PID控制器是通过对偏差进行运算获得控制值U(t)。PID运算包含3部分，第1部分为比例控制Proportional，比例控制器为一个增益(放大)器，其将输入信号放大Kp倍，Kp称为增益(放大)系数，增加Kp可提高系统准确性，降低系统惯性，但会影响控制稳定性。第2部分为积分控制器Integral，增加积分控制器参数Ki可以减小控制系统的稳态误差，但有可能引起系统振荡。第3部分为比例微分控制器Derivative，改变Kd可影响系统响应速度，即影响控制系统的快速性[16]。

在模拟中，考虑到非定常CFD计算的物理时间步长远远小于舵机的响应时间，因此假设舵面每隔Td接受一次控制信号。在Td时间内，舵偏规律设为

(8)

式中：Δd为需要接受控制指令后舵面需要偏转的总舵偏角；d(t)为舵偏角关于时间的函数；int为取整函数。

1.5气动/运动/控制集成流程

数值虚拟飞行的核心流程是气动/运动/控制(CFD/RBD/FCS)耦合求解。其中，CFD模块采用非定常方法求解获得每一物理时间步飞行器受到的气动力和力矩。刚体运动(RigidBodyDynamics，RBD)模块根据力和力矩情况，求解刚体6DOF方程，更新物体位置(网格坐标)。

本文使用松耦合算法[17]求解刚体动力学方程与流动控制方程的耦合问题，采用龙格库塔法求解动力学方程，采用双欧法求解飞行器姿态变化。在获得刚体下一时刻的位移和姿态角后，由式(9)获得n+1时刻的网格点坐标为

Rn+1=Ln+1·R0

(9)

式中：Ln+1为由n+1时刻的姿态角确定的转换矩阵；R0为初始的网格坐标。

控制系统(FlightControlSystem，FCS)模块根据飞行器姿态与期望的偏差形成反馈控制，结合重叠网格等动网格技术控制气动操纵面，控制飞行器姿态。然后再反复上述过程，直到运动结束。流程如下：

1) 为减小计算时间，采用定常计算获得初始流场。

2) 以初场为基础开展非定常流动计算。

3) 每推进一个物理时间步，求解飞行器的气动力和力矩，代入RBD求解获得物体位移，更新整体网格位置。

4) 根据FCS，控制操纵面运动，更新操纵面物体(网格)位置。

5) 开展下一物理时间步流场计算，重复步骤2～5，直至物理时间推进结束。

2　数值方法验证

用三维的超声速弹道外形[18](HyperBallisticShape，HBS)对程序和方法的正确性和可信度进行验证。HBS外形如图2所示，具有试验数据可供对比，是一个广泛用于超声速动态非定常计算程序验证的标准算例。

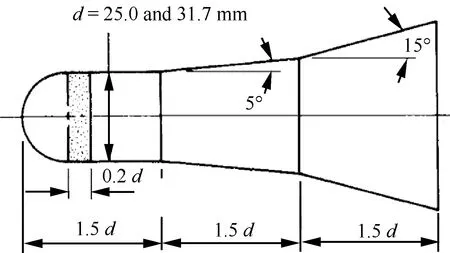
图2　超声速弹道模型外形及尺寸Fig.2　Shape and size of HBS model

采用文献[18]中来流参数开展计算，具体为：来流马赫数6.85，质心在弹长0.72倍处，以前段直径d为特征长度的雷诺数为0.72×106。对比在0°、5°、10°、15°和20° 迎角下计算和试验获得的俯仰导数，俯仰动导数采用振幅为1° 的正弦强迫运动计算获得，强迫运动的减缩频率取0.01，计算物理时间步长为2ms。图3(a)为计算获得的静导数Cmα同试验值对比，程序准确计算出了约在8° 迎角附近导数符号的改变。图3(b)为俯仰动导数同试验值对比，计算同试验数据符合较好，表明本文程序和非定常方法是可行的。

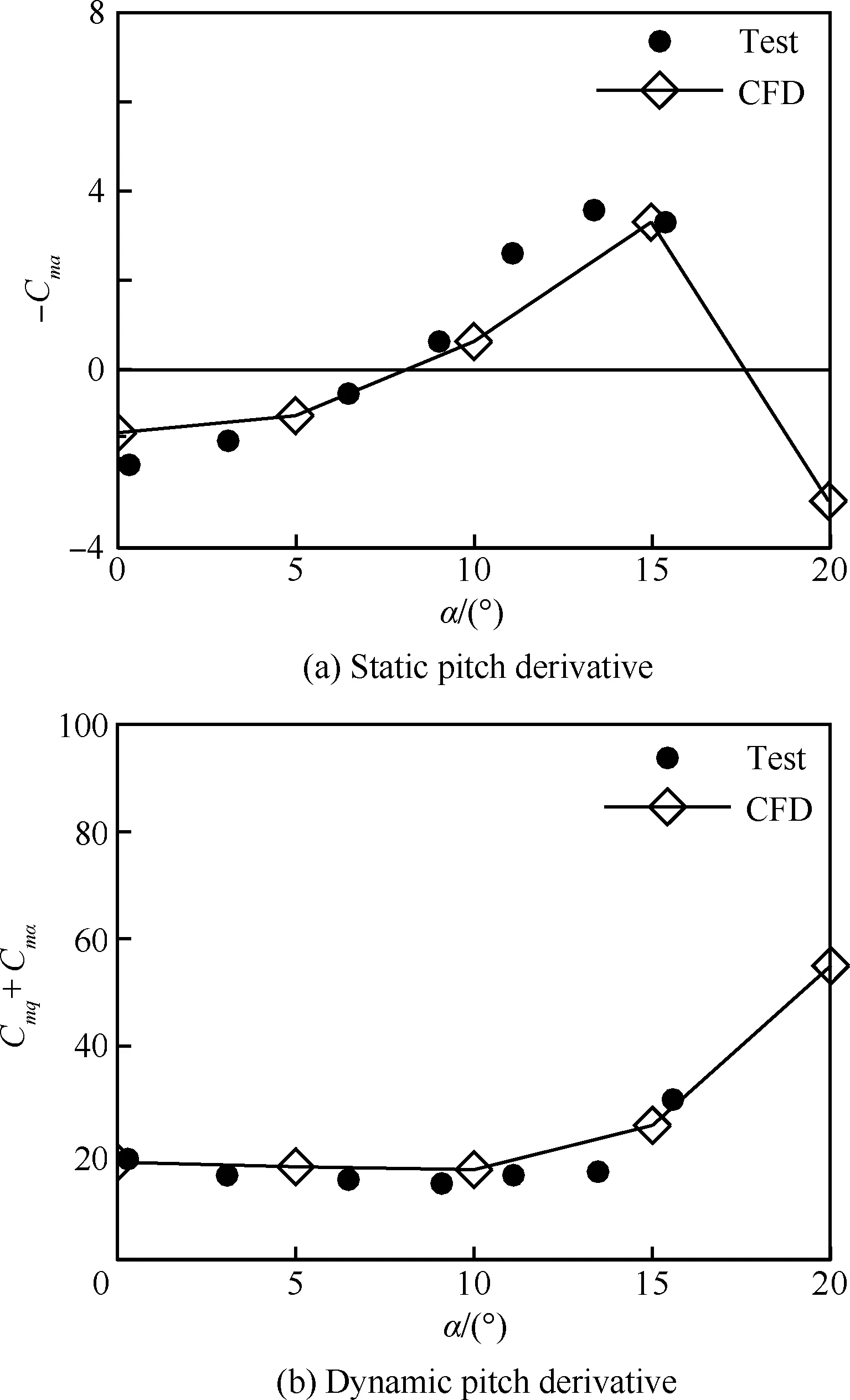
图3　HBS俯仰静、动导数计算与试验数据对比Fig.3　Comparison of computational static and dynamic pitch derivative with test data of HBS

3　数值模拟结果及分析

3.1返回舱外形平面运动动态特性研究

起源号返回舱网格如图4所示，具体外形尺寸见文献[19]，模型物理参数见表1。

图4　起源号返回舱表面及对称面网格Fig.4　Surface and symmetry plane grid of Genesis capsule

表1　起源号返回舱模型物理属性

Table 1　Physical property of Genesis capsule model

ItemValued/mm69.42M/g633Izz/kg·m23.01×10-4Iyy/kg·m21.99×10-4L/mm44.33Xcg/mm23.83

图5为初始马赫数Ma0为4.5，释放迎角为0.5° 时返回舱总迎角随射程变化规律同文献数据对比。由图可见，该状态弹道的前段总迎角较小，在120 m后迎角开始发散，计算也出现了相同的趋势。需要说明的是，文献中并未说明返回舱释放的角速度，计算时设初始角速度为零，从结果来看这不会对后段弹道迎角发散这一规律产生较大影响。图6为Ma=3.5，大气参数为海平面时，采用CFD自由振荡计算获得的动导数同文献[19]中数据对比。计算结果同文献数据接近，符合该返回舱在马赫数大于2.5时在大迎角下为动稳定的结论。

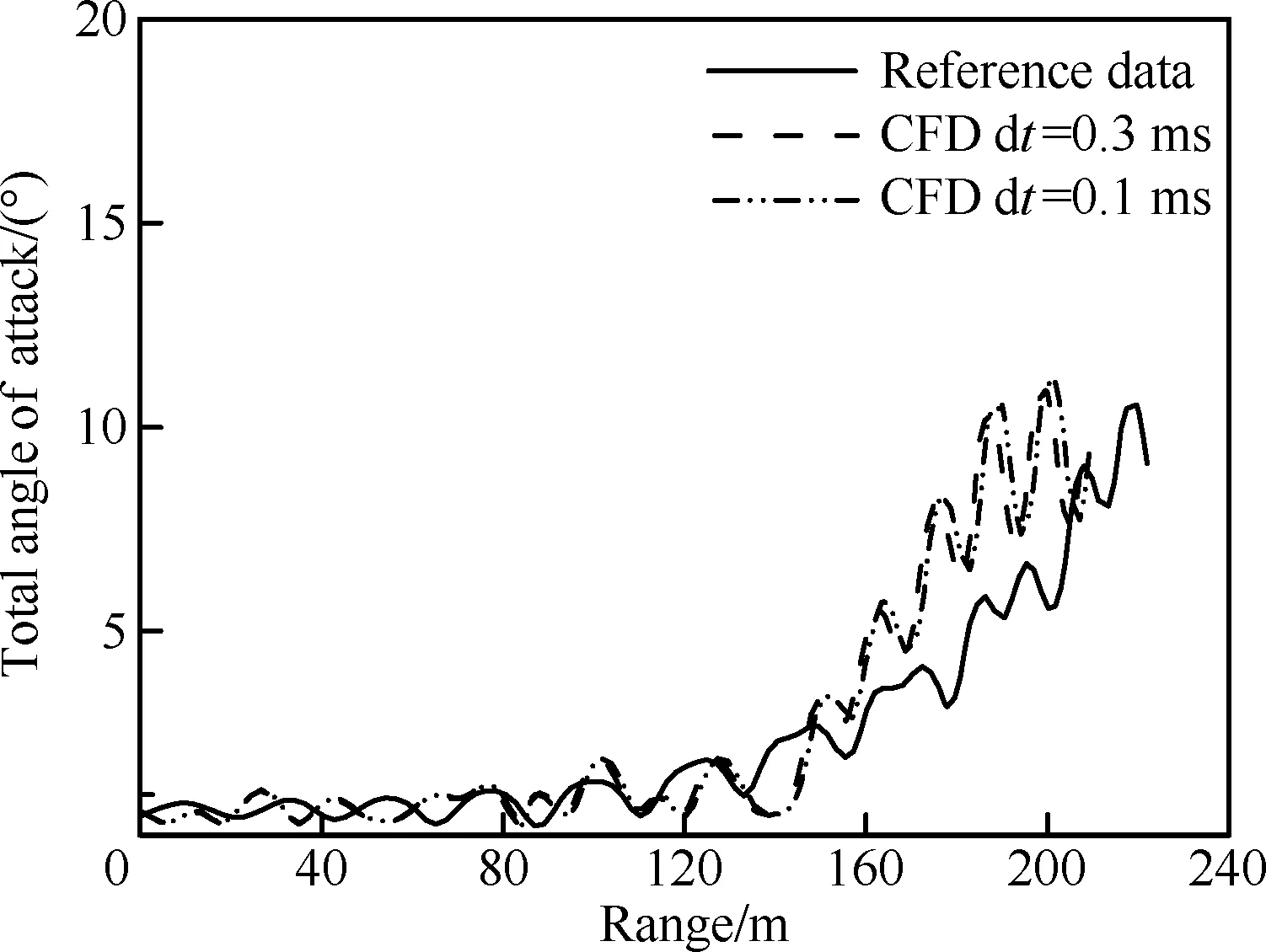
图5　Ma0=4.5，释放迎角为0.5° 时，返回舱总迎角随弹道变化规律计算与试验对比Fig.5　Comparison of computational trajectory history of total angle of attack with test data at Ma0=4.5 and release α=0.5°

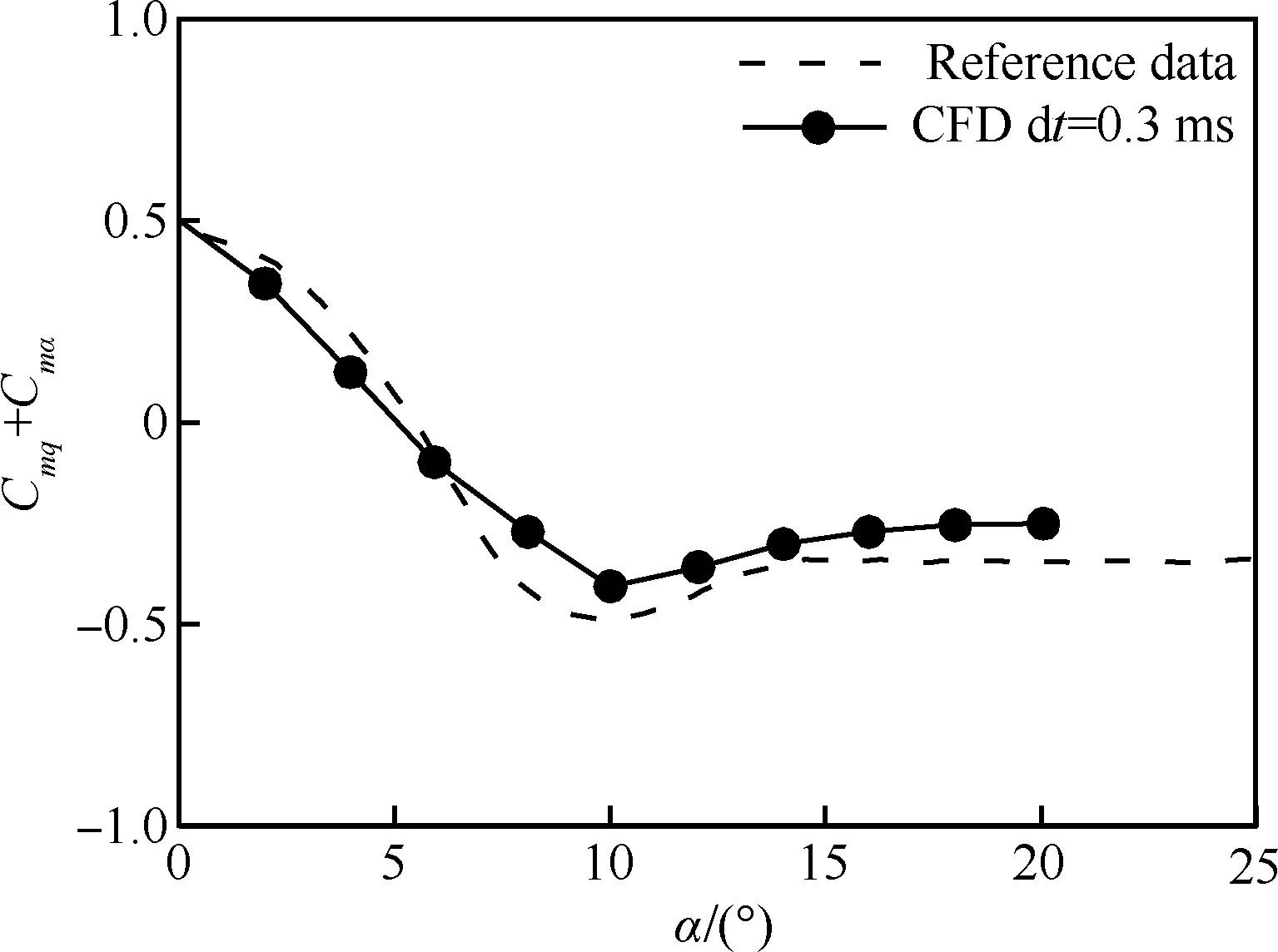
图6　Ma=3.5时，返回舱俯仰动导数计算同文献对比Fig.6　Comparison of computational capsule dynamic pitch derivative with reference data at Ma=3.5

以上计算结果同试验结果吻合良好，可确定本文方法的正确性。下面的研究主要关注不同自由度运动对返回舱运动特性的影响，因此本外形算例来流参数统一为：来流马赫数为3.5，飞行高度为25 km，来流压力、温度根据地球大气参数表获得，计算皆采用层流假设，物理时间步长统一取为0.3 ms。由于自由俯仰运动时，该系统是自治系统，其极限环状态(振幅和频率)与初值无关，因此，为了较快出现极限环运动，计算预置10° 迎角，并且设置返回舱的质量为表1中的1/4，以减小惯量，使运动迅速出现振荡，以节约计算时间。

3.1.1平面单自由度俯仰运动

当返回舱绕质心做单自由度俯仰振动时，其动力学方程为

(10)

在某迎角的小的邻近范围内，可以假设俯仰静、动导数为常量，则式(10)为一典型的二阶阻尼系统，其解析解为

(11)

式中：ξl为阻尼；ωl为振动频率，具体表达式为

(12)

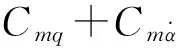
图7为返回舱的静、动导数随迎角变化情况。由图可见，各迎角下该外形静导数变化不大，而动导数在小迎角处是正值，表现为动不稳定；迎角大于5° 后，动导数变为负值，表现为动稳定。因此，返回舱在小迎角下受到扰动，由于动不稳定性，扰动振幅将增大，在大迎角时，气流起阻尼作用，从而衰减振幅。在一定条件下，这样的动导数变化规律可使得飞行器出现俯仰极限环振荡状态。

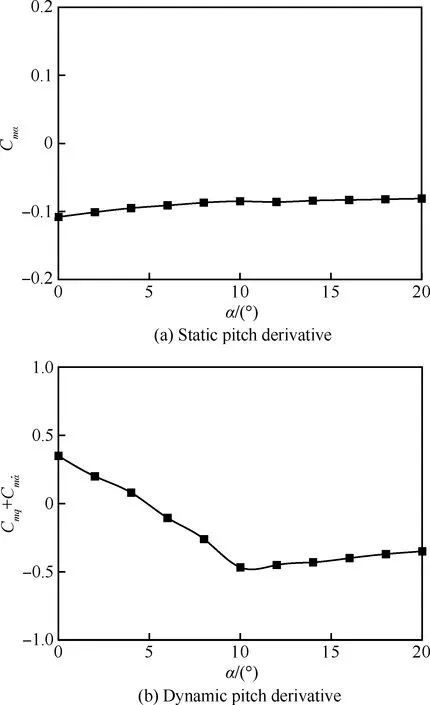
图7　“起源号”返回舱各迎角下俯仰静、动导数Fig.7　Static and dynamic pitch derivative of Genesiscapsule under different angles of attack

图8为自由俯仰振荡迎角随时间的变化规律。可见，由前述动导数特性，从10° 迎角释放外形后，飞行器振幅逐渐增加，当振幅达到15° 左右时，飞行器出现等周期的极限环振荡。

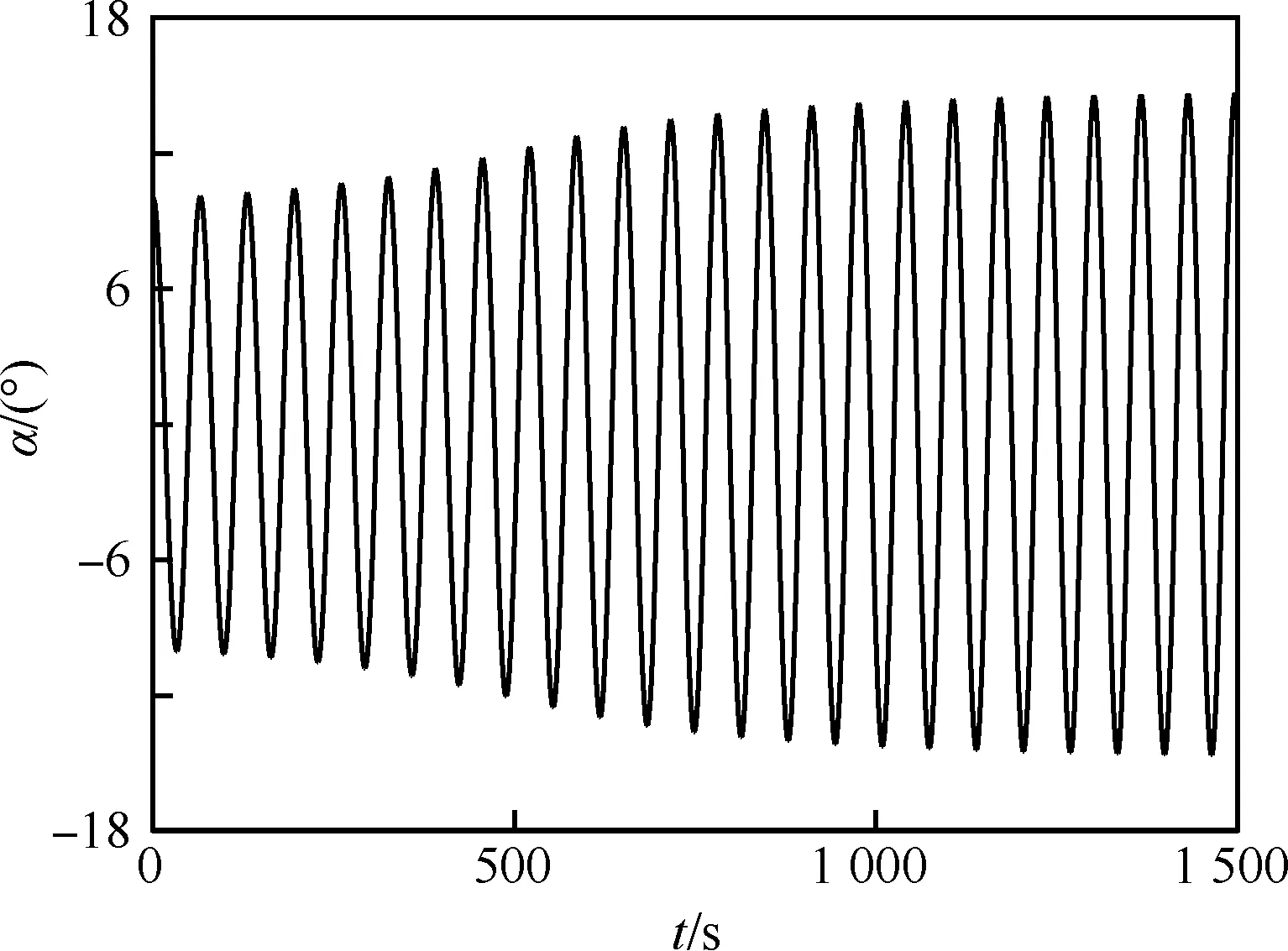
图8　自由俯仰运动迎角随时间变化规律Fig.8　Time history of angle of attack of free pitching motion

3.1.2平面俯仰+沉浮双自由度运动

下面研究引入质心沉浮运动后，返回舱的运动特性。图 9为双自由度和单自由度运动下飞行器迎角随时间变化规律。由图可见，引入沉浮运动后，返回舱仍形成等周期和振幅极限环俯仰振动，但相比单自由度振动，其振幅加大，频率减小。

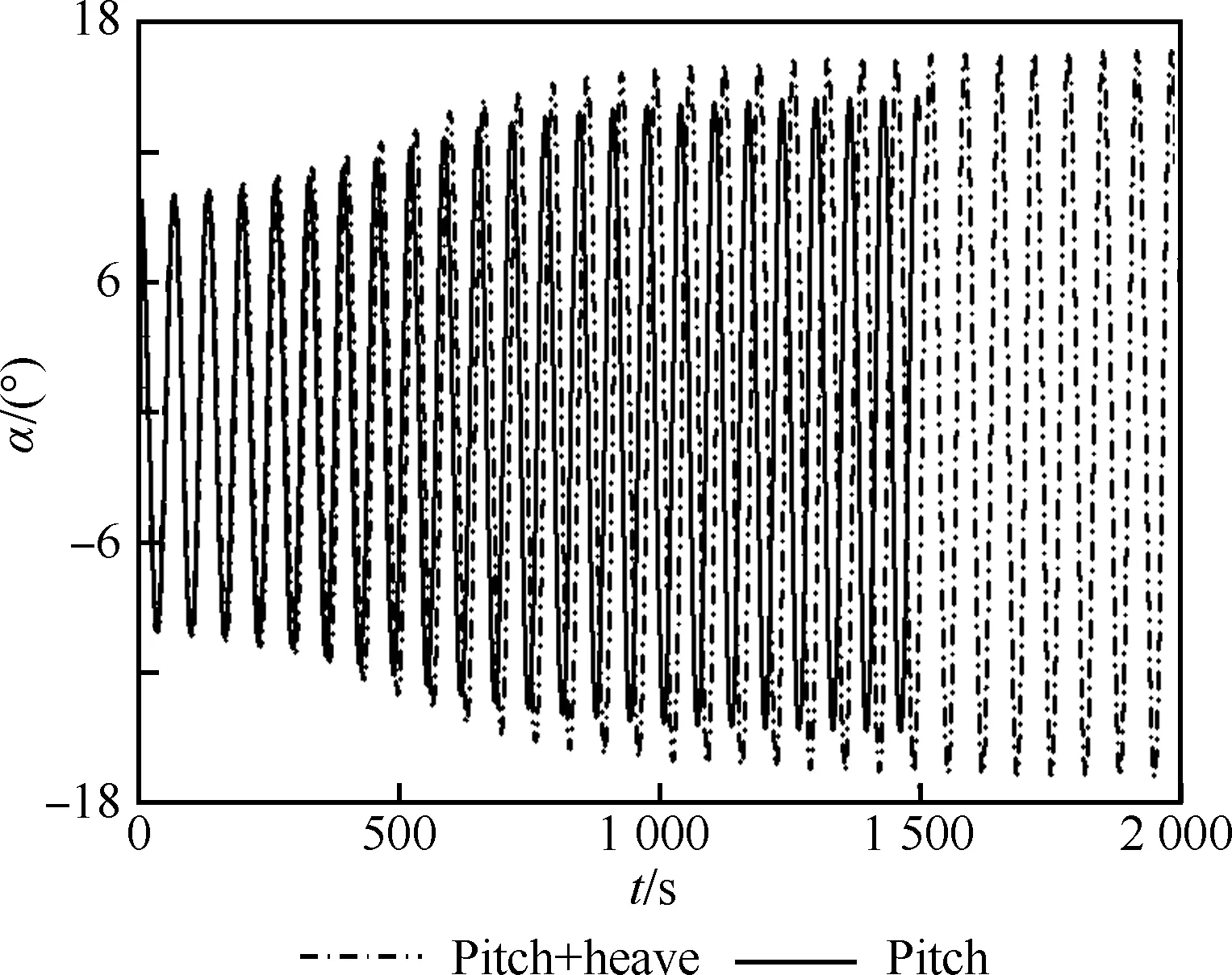
图9　双自由度和单自由度运动下迎角随时间变化规律的对比Fig.9　Comparison of time histories of angle of attack of one and two DOF motion

图10为返回舱质心沉浮速度V随时间变化规律，其与迎角随时间变化有1/4周期的相位差。此外，注意到，由沉浮运动引起的迎角变化不会超过0.02°，这表明引起俯仰振动频率和振幅变化的主要原因并不是沉浮速度，而是引入沉浮运动后，系统阻尼变小导致的，这跟文献中理论分析一致[20-21]。返回舱平面双自由度运动下的俯仰静、动导数及失稳特性和单自由度运动的类似，在此不再赘述。

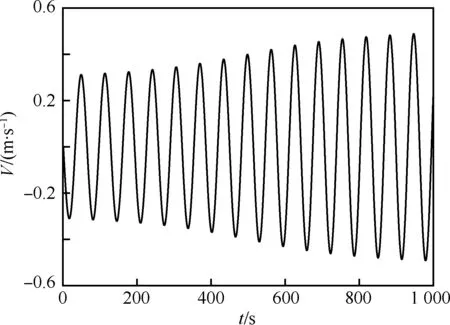
图10　返回舱双自由度运动质心沉浮速度随时间的变化规律Fig.10　Time history of centroid velocity of two DOF motion of return capsule

3.1.3平面自由飞三自由度运动

返回舱返回时，在气动阻力的作用下减速运动，引入流向运动自由度，即可考察返回舱平面自由飞行的动态特性，这种自由飞更加接近真实飞行情况。图11为平面自由飞运动下飞行器迎角随时间的变化规律。由图可见，考虑气动阻力后，返回舱振幅更大，这表明飞行器变得更为动不稳定。此外，可以看出，振荡频率逐渐减小，振荡周期变长，这是由于气动阻力使飞行器速度降低造成的。

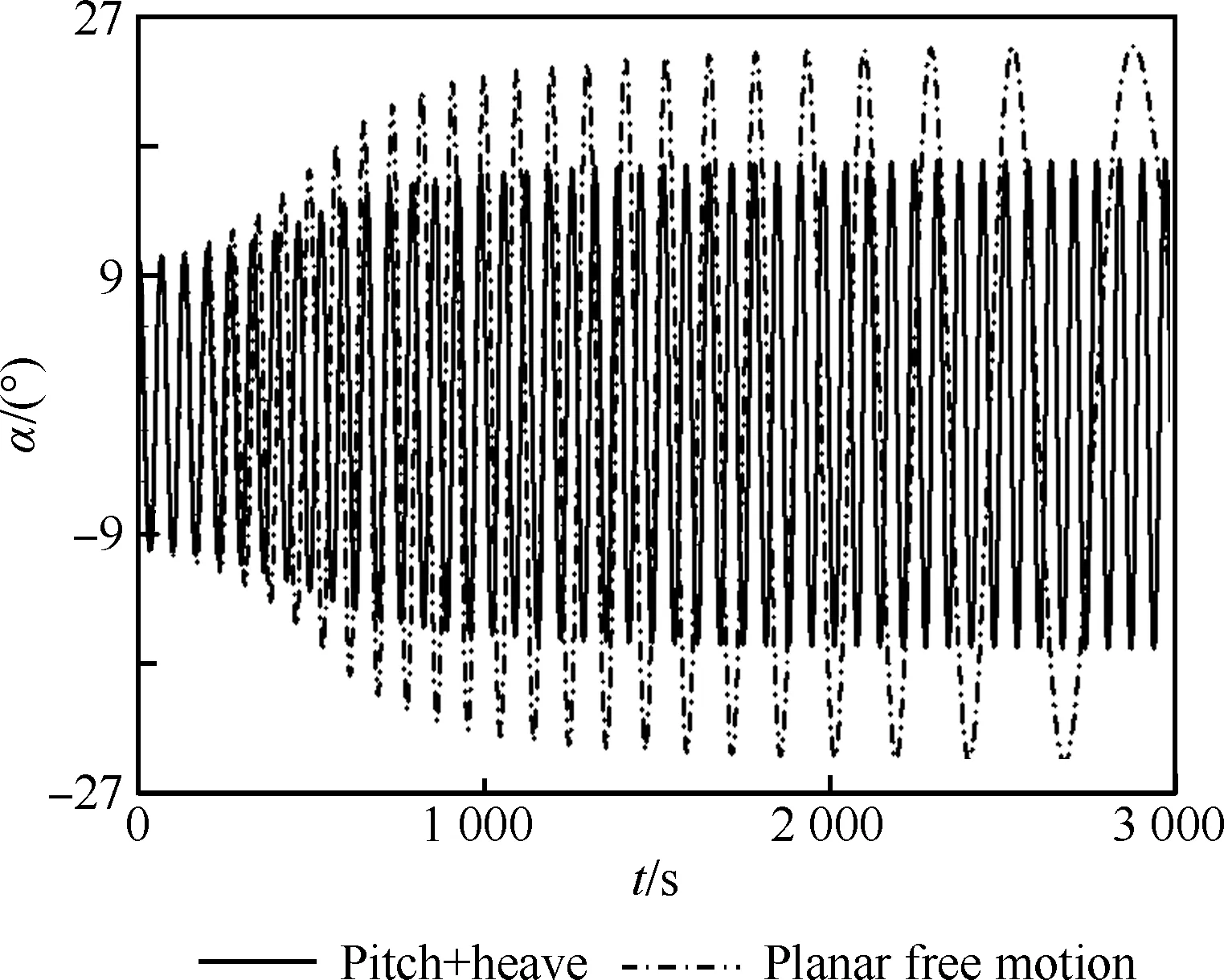
图11　平面自由飞和双自由度下迎角随时间的变化规律对比Fig.11　Comparison of time histories of angle of attack of planar free and two DOF motion

图12为平面自由飞运动下返回舱质心沉浮速度随时间的变化规律。可见，自由飞下沉浮速度振幅比双自由度运动下的振幅有所增加，且周期逐渐变长。图13为质心流向速度随时间的变化规律，空气阻力的存在使飞行器流向速度由3.5马赫降到了2.2马赫左右。同样，基于自由飞计算开展参数辨识，也可获得相应的静、动导数，在此不再累述。

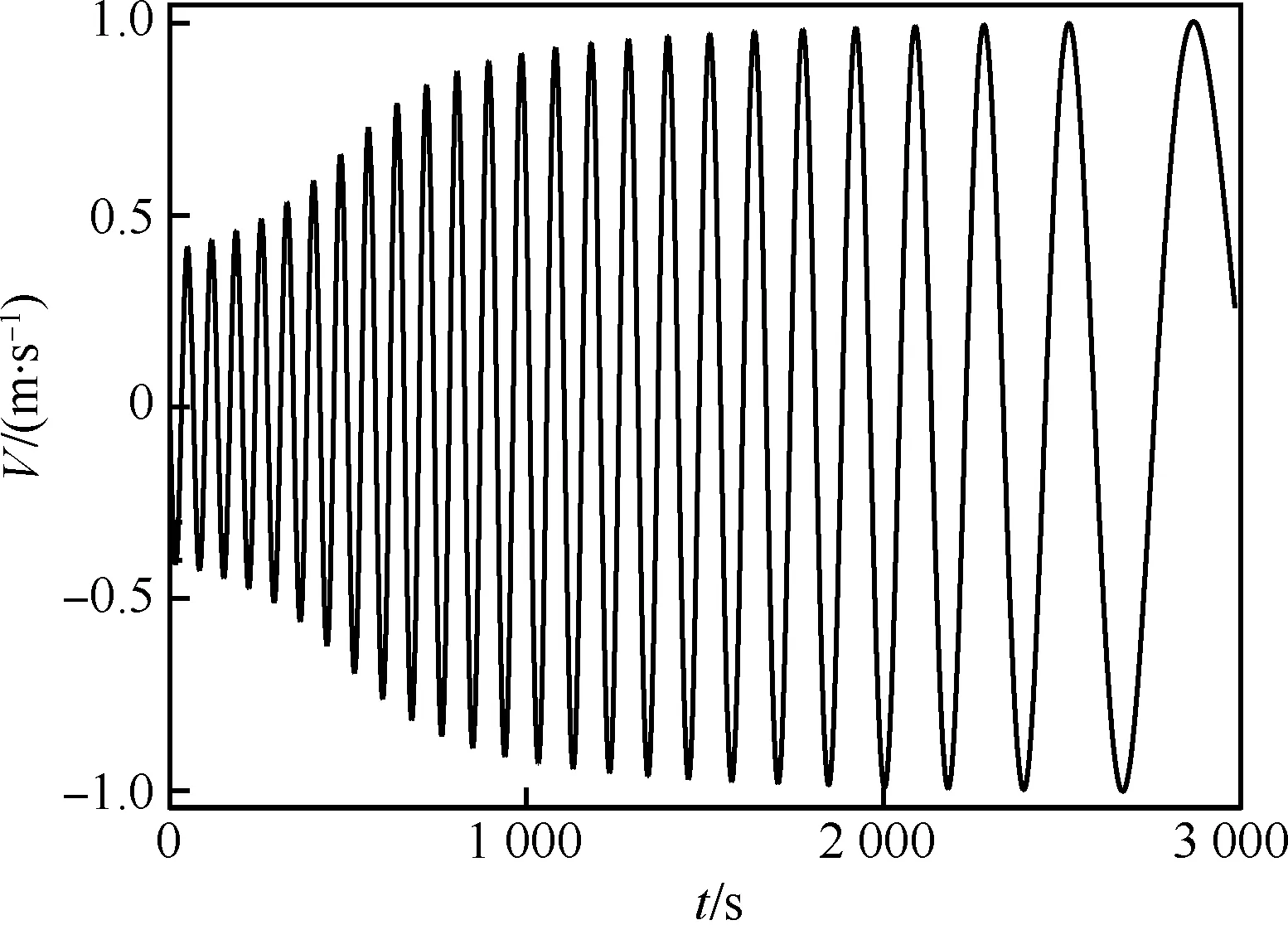
图12　平面自由飞质心沉浮速度随时间变化规律Fig.12　Time history of centroid velocity of planar free motion

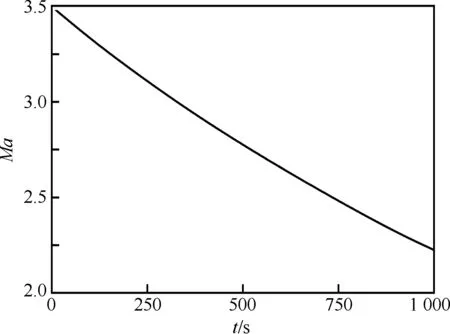
图13　平面自由飞质心流向速度随时间变化规律Fig.13　Time history of flow direction centroid velocity of planar free motion

3.2受控导弹纵向数值虚拟飞行模拟

计算外形为尾部安装有4个翼的导弹。该外形具有大量的静、动态试验数据及计算对比数据[22-23]。该导弹外形涵盖了大部分战术导弹的典型气动布局特征。导弹为十字翼布局，尾舵为均匀厚度。计算外形尺寸及舵号定义见图14(图中CG为模型重心)，模型物理参数见表 2。图15为Ma=4.42，Red=2.96×107时采用不同时间步长计算获得的俯仰角随射程变化规律同试验值之间的对比，其中Red是以弹身直径d为特征长度的雷诺数；图 16为Red=8.6×106，Ma=1.96，无量纲质心位置X/d=6.1时导弹各迎角下动导数计算与试验对比。以上计算结果同试验结果吻合良好，可确定本文方法的正确性。此外由图 15可见，采用0.5 ms和1 ms时间步长的计算结果同试验值得差异皆不大，因此为减少计算机时，之后计算中物理时间步长均取1 ms。本文只考虑俯仰通道模拟，因此只考虑1号和2号舵实现舵偏功能，舵后缘向下偏转定义为正舵偏，采用重叠网格实现舵偏功能。此外，在下述计算皆采用一方程的Spalart-Allmaras湍流模型模拟湍流黏性，子迭代收敛残差取为0.01。

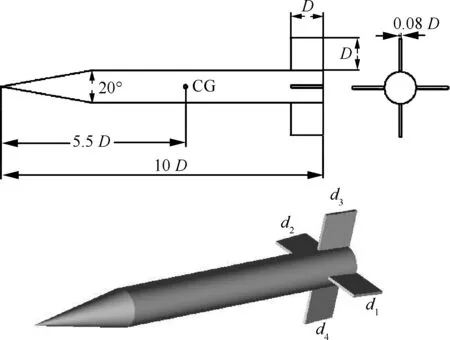
图14　基本带翼导弹模型外形及尺寸Fig.14　Shape and size of basic finner

表2　基本带翼导弹计算模型物理属性

Table 2Physical property of calculation model of basic finner

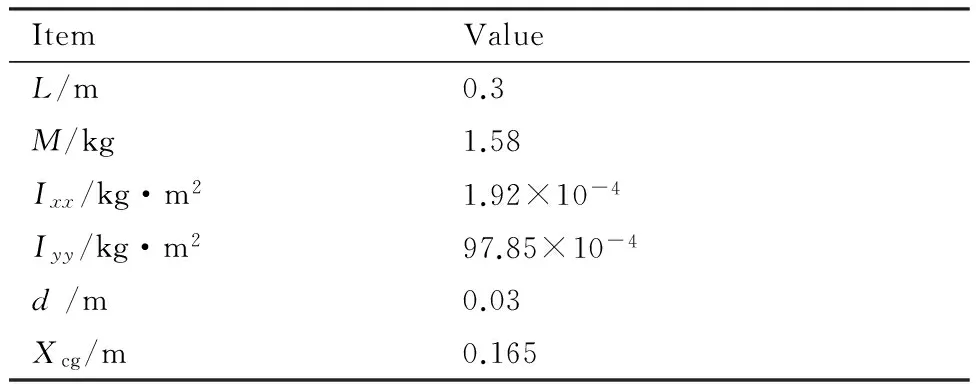
ItemValueL/m0.3M/kg1.58Ixx/kg·m21.92×10-4Iyy/kg·m297.85×10-4d/m0.03Xcg/m0.165

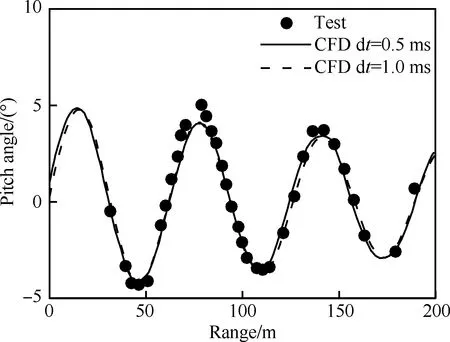
图15　导弹俯仰角随射程变化计算同试验值对比Fig.15　Comparison of computational projectile pitch angle variation with range and test data

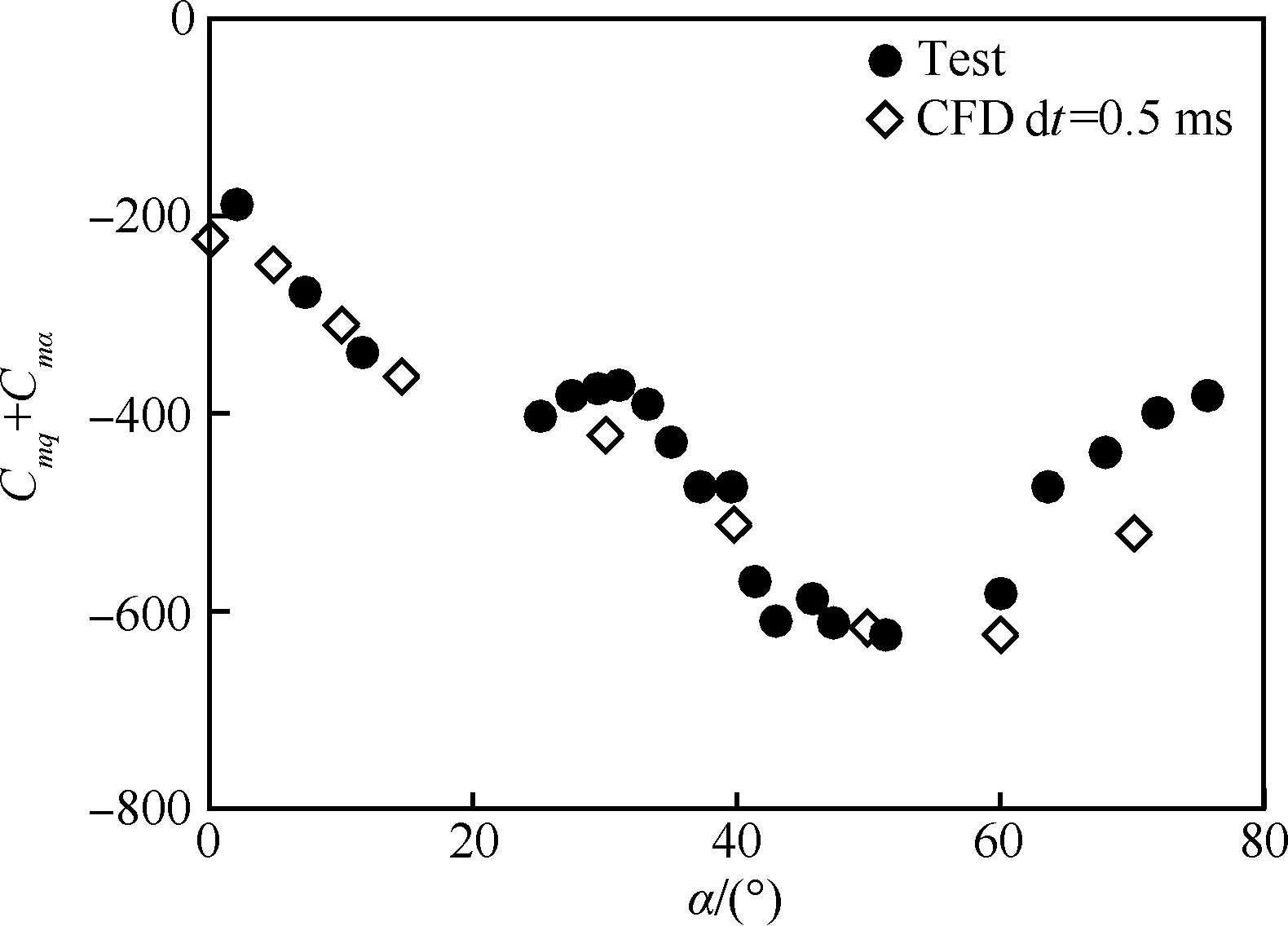
图16　Red=8.6×106时动导数计算试验值对比Fig.16　Comparison of computational dynamic derivative with test data at Red=8.6×106

3.2.1飞行器姿态稳定特性研究

飞行器的稳定特性包括动稳定性和动操纵性。当飞行器受外界扰动后的运动体现其动稳定性，当飞行器受操纵力控制后的运动体现其动操纵性。设计扰动规律，开展飞行器姿态稳定研究，可以检验飞行器不同的运动模态，测试飞行器在各种极端情况下的静、动稳定性，且可为气动参数辨识提供足够的信息。

采用时域法分析一个系统的性能，一般采用一些典型的输入作为测试信号，如阶跃输入，脉冲输入等[16]，结合导弹飞行的特点，本文选取如下4种舵偏规律作为扰动输入，测试基本外形导弹在不同舵偏扰动下的姿态稳定性：

1) 阶跃型舵偏输入

d(t)=5°t≥0

(13)

2) 方形脉冲舵偏输入

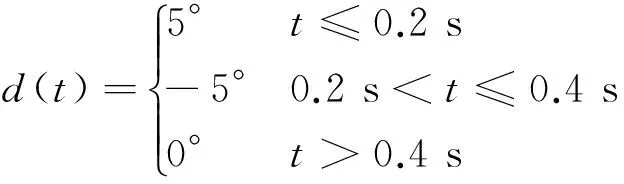
(14)

3) 梯形舵偏输入

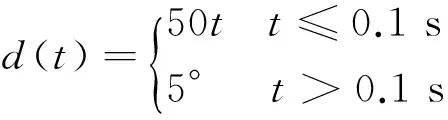
(15)

4) 正弦舵偏输入

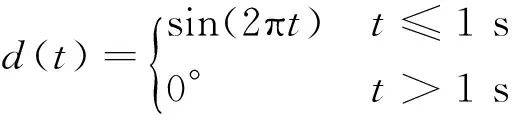
(16)

式中:d(t)为舵偏角随时间的函数;t为物理时间。下面计算中来流条件为Ma=2，高度为10 km，来流压力及密度根据大气参数表获得，飞行器初始迎角为0°,无姿态角速度及姿态角加速度。

基于小扰动理论，基本外形导弹带舵面控制的无量纲纵向运动方程可写为

(17)

式中：Iz为转动惯量；θ为俯仰角。

式(17)的特征方程为

(18)

图17为阶跃舵偏下导弹俯仰角响应曲线及俯仰角速度响应曲线。阶跃舵偏反映了舵偏(扰动)突变的一种极限情况，而飞行受扰动后收敛于平衡位置的过程反映了飞行的动稳定性。由图可见，阶跃舵偏(扰动)引起的角速度达200°/s左右，飞行器俯仰角振荡收敛到-5.5° 左右，振荡次数、幅度衰减情况反映了飞行器的操纵品质。式(17)在阶跃舵偏下的解为

(19)

式中：αeq为配平攻角；φ为相位裕度，具体表达式为

(20)

结合式(18)与式(19)，即可辨识出俯仰阻尼导数等参数。

图18为偶极脉冲舵偏下导弹俯仰角响应曲线及俯仰角速度响应曲线。在t=0.2 s时，此时导弹具有正俯仰角速度，0.2 s时刻后，舵偏变负，产生的抬头力矩加剧了抬头的趋势。当干扰频率与飞行器固有频率接近时，可能引起飞行器共振。偶极脉冲舵偏可反映飞行器受到瞬时、随机且频率接近飞行器固有频率的干扰的动态性能。

图19为梯形脉冲舵偏下导弹俯仰角响应曲线及俯仰角速度响应曲线。梯形脉冲舵偏反映了等速舵偏与阶跃舵偏的组合情况。由图可见，此时超调量小于阶跃型舵偏，且振动频率也小于阶跃型舵偏，最大俯仰角速度约为100°/s，这种舵偏规律代表了缓慢的机动飞行。

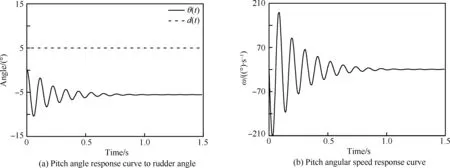
图17　阶跃舵偏下的俯仰响应曲线Fig.17　Pitch response curve of phase step impulse rudder deflexion

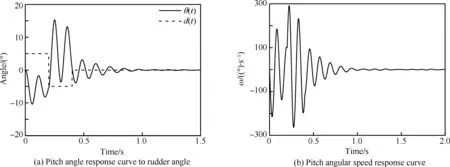
图18　偶极脉冲舵偏下的俯仰响应曲线Fig.18　Pitch response curve of dipole impulse rudder deflexion

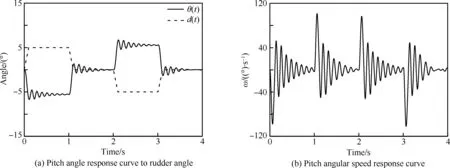
图19　梯形脉冲舵偏下的俯仰响应曲线Fig.19　Pitch response curve of echelon impulse rudder deflexion

图20为谐波脉冲舵偏下导弹俯仰角响应曲线及俯仰角速度响应曲线。由图可见，此种情况下，舵偏(扰动)引起的最大俯仰角速度及俯仰力矩相对前3种情况是最小的，此时飞行器实施精确跟踪，处于理想化的反复修正过程。

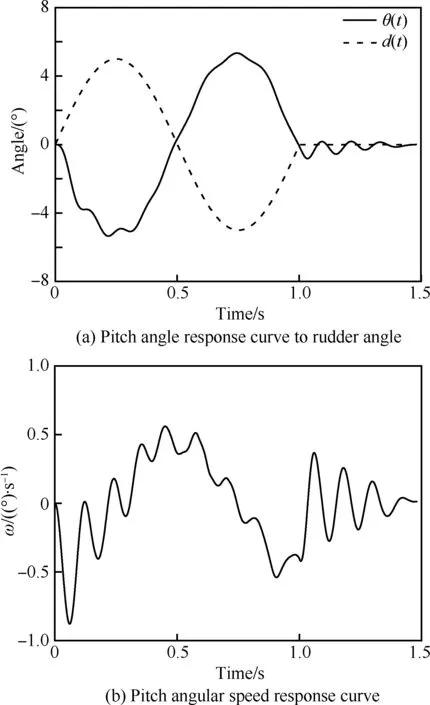
图20　谐波脉冲舵偏下的俯仰响应曲线Fig.20　Pitch response curve of harmonic wave impulse rudder deflexion

3.2.2基于数值虚拟飞行对控制参数的整定

飞行器在飞行过程中，控制系统会根据飞行状态发出实时控制指令，修正飞行姿态。系统受控后，要么导致受控发散，要么趋于受控状态。飞行器是否会出现受控发散，即控制是否具有稳定性，可以采用3.3.1节中的方法检验。而对于受控稳定情况，则要考虑控制系统的准确性，快速性及平稳性。

控制系统的准确性，快速性及平稳性与控制系统的参数有很强的关系。同一种控制方式，面对各种各样的飞行器，满足上述要求的控制参数也大不相同。即使对于同一个飞行器，由于飞行过程中燃料消耗导致的质量、惯性矩及重心的物理参数的改变，也会使飞行器受控后响应发生改变。而对于处于非定常/非线性流动下的飞行器，气动力、力矩的突变、迟滞特性更会使得基于线化气动导数等参数获得控制参数不能在全范围内保证控制的稳定、准确、快速及平稳性。因此，整定控制参数，是数值虚拟飞行一个重要的应用，也是风洞等常规手段难以实现的。

本文采用PID控制器，实现舵偏反馈控制，跟踪指定迎角规律。测试了不同PID参数(如表3 所示)下导弹的纵向受控性能，以获得较好的控制参数。

模拟的来流条件为：Ma=2，高度为10 km，初始迎角为a=0°，初始俯仰角速度为零，角加速度也为零。导弹姿态角变化要求为：机动到5° 迎角飞行，超调不超过20%，并维持姿态稳定。按上述要求及计算模型物理属性，根据PID控制理论[16]，选取如下范围的PID控制参数及舵受控时间Td，对该范围的参数整定，以达到最佳控制效果。

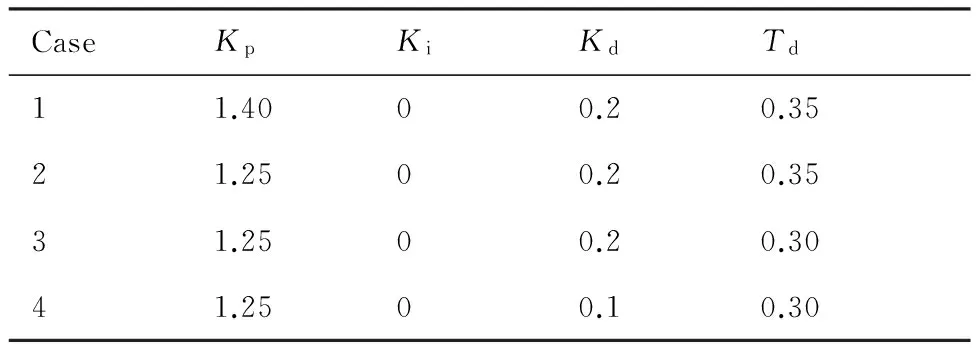
表3　PID控制参数

图21～图24为各控制参数下导弹的响应时间历程。从图中可以看到，控制系统根据飞行器姿态角的误差发出控制指令，控制舵面，飞行器实施机动，然后反复调节，直至飞行器达到期望姿态。由相图可见，初始阶段，飞行器的俯仰角速度增加，迎角也随之增加，当迎角接近指定值5° 时，微分控制器开始制动，减小俯仰角速度，当姿态角度超过5° 后，在控制器作用下，舵面反复调整，使得俯仰角速度变负，最后逐渐收敛于相图上的螺旋点。

对比Case 1和Case 2可以看出，Case 1超调量约20%，Case 2超调量约10%，Case 1的最大俯仰角速率约为33°/s，而Case 2为30°/s。这表明增加Kp，会提高系统的响应速度，但会使得超调增加，振荡过渡过程变长。对比Case 3和Case 4相图可以看出，在迎角达到2° 左右时，控制系统开始制动，即减小俯仰角速率。制动后Case 3的最大俯仰角速率为39°/s，Case 4的最大俯仰角速率为42°/s。这表明增加Kd，使得系统的制动提前，降低俯仰角速度峰值，能减少过渡振荡过程。对比Case 2和Case 3，Td减小加快了俯仰角速率，提高了系统响应速度。

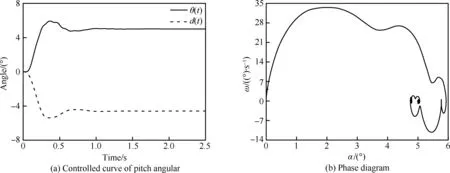
图21　Case 1的俯仰响应曲线Fig.21　Pitch response curve of Case 1

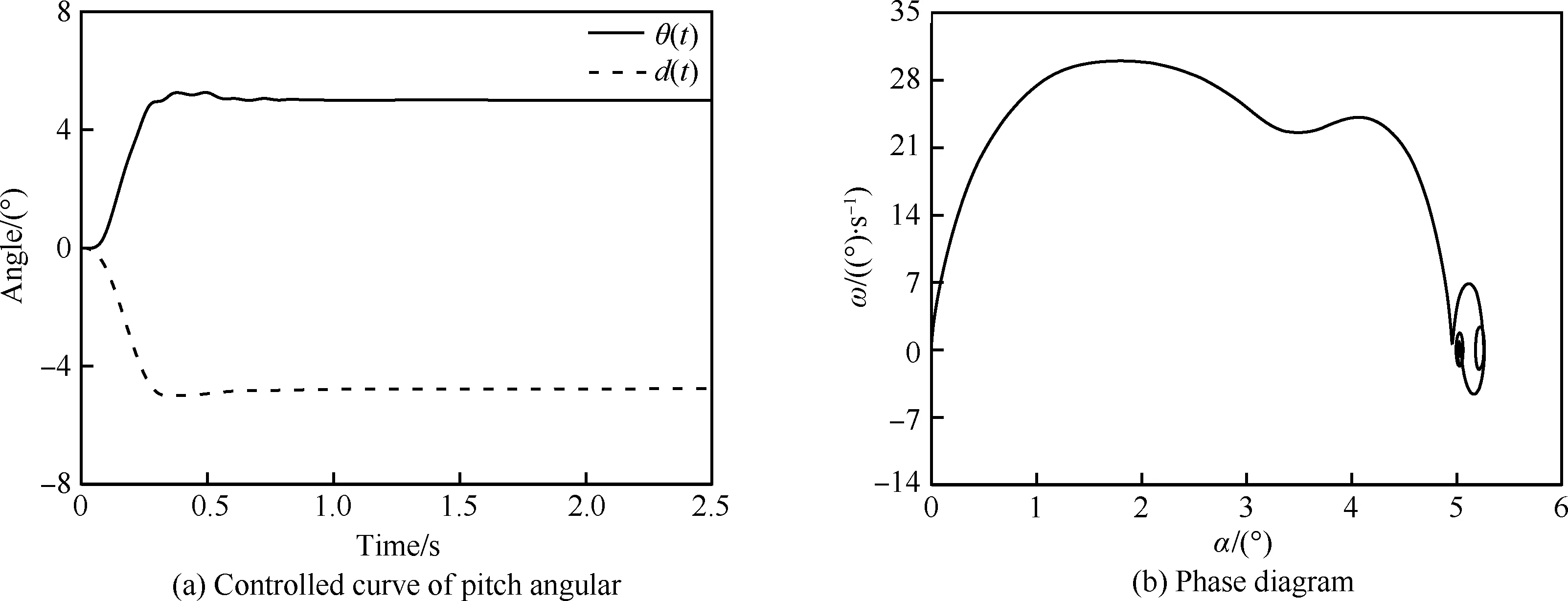
图22　Case 2的俯仰响应曲线Fig.22　Pitch response curve of Case 2

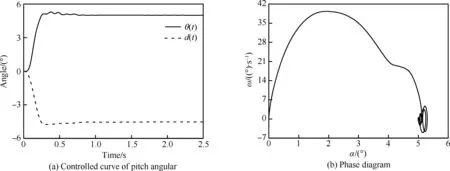
图23　Case 3的俯仰响应曲线Fig.23　Pitch response curve of Case 3

上述算例表明，Case 3的控制参数有较好的特性。下面采用Case 3控制参数对有初始俯仰角速度的状态进行控制，验证控制效果，初始俯仰角速度设为50°/s。

图25为采用Case 3的控制参数下的俯仰角控制曲线和相图。导弹在初始俯仰角速度的作用下，迎角增加。由于导弹是静、动稳定，且此时舵偏角较小，俯仰角速度迅速减小变为负值。当舵偏角负向变大时，产生抬头力矩，迎角增加，然后逐渐调整到预设迎角。初始俯仰角速度的存在使得弹体动阻尼效应较为明显，且初始角速度越大，动态效应表现越强。

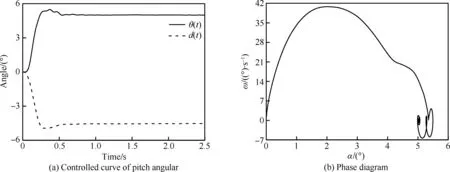
图24　Case 4的俯仰响应曲线Fig.24　Pitch response curve of Case 4

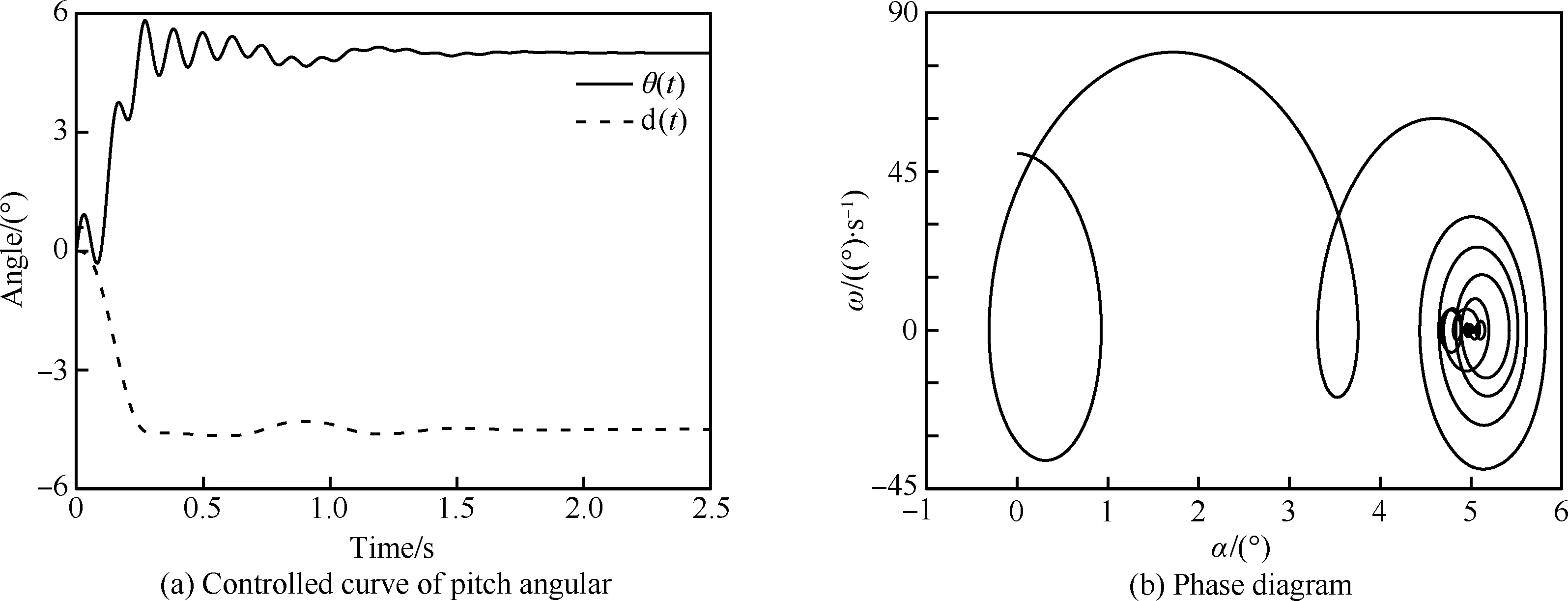
图25　有初始俯仰角速度时的俯仰响应曲线Fig.25　Pitch response curve of state with initial pitching angular speed

4　结　论

本文利用数值虚拟飞行技术，对返回舱外形及受控基本带翼导弹外形开展了动态特性研究。

对返回舱外形的研究表明：返回舱外形具有静态稳定性和动不稳定性。对于平面三自由度俯仰运动，俯仰阻尼导数决定了返回舱的动稳定性。引入沉浮运动使得返回舱动稳定性变差。引入流向自由度后，气动阻尼使飞行器速度降低，动稳定性变差，且极限环周期逐渐变长。

对受控基本外形导弹的研究表明：通过输入典型的扰动(舵偏)信号，可以检测导弹系统的稳定、受控性能。不同控制参数对系统的控制性能有较大影响。增大增益系数，可以提高响应速度，但会增加超调量，引起振荡。增加微分系数，可以控制系统制动幅度及时间，减小超调量，使振荡过渡过程尽快结束。

上述研究表明，结合结构重叠网格技术、闭环控制律的数值虚拟飞行技术能够有效地研究常规手段无法研究的飞行器动态特性问题。其应用灵活性好，周期短，对探索飞行器气动/运动耦合问题，控制参数的整定，控制律的研究和检测，获取飞行器非定常的运动导数以及飞行的安全性测试具有较好的工程应用价值及应用前景。

[1]吕光男. 风洞虚拟飞行实验中的飞行力学与控制问题研究[D]. 南京: 南京航空航天大学, 2009： 1-13

LYU G N. The problem of flight mechanics and control in wind tunnel based virtual flight testing[D]. Nanjing: Nanjing University of Aeronautics and Astonautics, 2009:1-13 (in Chinese).

[2]李周复. 风洞特种实验技术[M]. 北京: 航空工业出版社, 2010: 210-250.

LI Z F. Special wind tunnel testing technology[M]. Beijing: Aviation Industry Press, 2010: 210-250 (in Chinese).

[3]刘伟, 杨小亮, 赵云飞. 高超声速飞行器加速度导数数值模拟[J]. 空气动力学学报, 2010, 28(4): 426-429.

LIU W, YANG X L, ZHAO Y F. Numerical simulation of acceleration derivative of hypersonic aircraft[J]. Acta Aerodynamica Sinica, 2010, 28(4): 426-429 (in Chinese).

[4]RATLIFF C L, MARQUART E J. An assessment of a potential test technique: virtual flight testing (VFT): AIAA-1995-3415[R]. Reston: AIAA, 1995.

[5]GEBERT G, KELLY J, LOPEZ J. Wind tunnel based virtual flight testing: AIAA-2000-0829[R], Reston: AIAA, 2000.

[6]MAGILL J C, CATALDI P, MORENCY J R, et al. Demonstration of a wire suspension for wind-tunnel virtual flight testing[J]. Journal of Spacecraft and Rockets, 2009, 46(3): 624-633.

[7]张来平, 马戎, 常兴华, 等. 虚拟飞行中气动运动和控制耦合的数值模拟技术[J]. 力学进展, 2014, 44: 201410.

ZHANG L P, MA R, CHANG X H, et al. Review of aerodynamics/kinematics/flight-control coupling methods in virtual flight simulations[J]. Advances in Mechanics, 2014, 44: 201410.

[8]阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006： 18-24.

YAN C. Computational fluid dynamics methods and applications. Beijing[M]. Beijing: Beihang University Press 2006: 18-24 (in Chinese).

[9]SALAS M D. Digital flight: The last CFD aeronautical grand challenge[J]. Journal of Scientific Computing, 2006, 28(2-3): 479-505.

[10]ROGERS S E,ROTH K,NASH S M,et al.Advances in overset CFD processes applied to subsonic high-lift aircraft: AIAA-2000-4216[R]. Reston: AIAA, 2000.

[11]GOETZ H K, JAMES E K, HENRY C L, et al. Validation of overflow for computing plume effects during the ARES I stage separation process: AIAA-2011-0170[R]. Reston: AIAA, 2011

[12]范晶晶, 阎超, 张辉. 重叠网格洞面优化技术的改进与应用[J]. 航空学报, 2010, 31(6): 1127-1133.

FAN J J, YAN C, ZHANG H. Improvement of hole-surface optimization technique in overset grids and its application[J]. Acta Aeronauticaet Astronautica sinica, 2010, 31(6)： 1127-1133 (in Chinese).

[13]袁武. 新型重叠网格方法研究及在复杂多体气动问题中的应用[D]. 北京： 北京航空航天大学, 2012: 24-35.

YUAN W. Investigations on novel chimera grid methods and its applications to complex multibody aerodynamic problems[D]. Beijing: Beihang University, 2012: 24-35 (in Chinese).

[14]肖业伦， 航空航天器运动的建模—飞行动力学的理论基础[M]. 北京： 北京航空航天大学出版社， 2003: 64-78.

XIAO Y L. Modeling of the motion of space vehicle—the basic of flight mechnics[M]. Beijing: Beihang University Press 2003: 64-78 (in Chinese).

[15]吴森堂, 费玉华. 飞行控制系统[M]. 北京: 北京航空航天大学出版社, 2009: 85-93.

WU S T, FEI Y H, Flight control system[M]. Beijing: Beihang University Press, 2009: 85-93 (in Chinese).

[16]MEI X R, ZHUANG X Y. Principle of auto control[M]. Beijing: Science Press, 2009: 54-61.

[17]栗长江. 高超声速飞行器多自由度动态特性研究[D]. 长沙: 国防科学技术大学, 2010: 51-54.

LI C J. Study of mutidimensional motion of hypersonic flight vehicle[D]. Changsha: National University of Science and Technology, 2010: 51-54 (in Chinese).

[18]EAST R A, HUTT G R. Comparison of predictions and experimental data for hypersonic pitching motion stability[J]. Journal of Spacecraft, 1988, 25(3): 225-233

[19]CHEATWOOD F, WINCHENBACH G, HATHAWAY W, et al. Dynamic stability testing of the genesis sample return capsule: AIAA-2000-1009[R]. Reston: AIAA, 2000.

[20]袁先旭. 非定常流动数值模拟及飞行器动态特性分析研究[D]. 绵阳: 中国空气动力研究与发展中心研究生部, 2002: 101-117.

YUAN X X. Numerical simulation for unsteady flowsand research on dynamic characteristicsof vehicle[D]. Mianyang: China Aerodynamics Research and Development Center. 2002: 101-117 (in Chinese).

[21]席柯. 虚拟飞行数值模拟方法及飞行器动态特性研究[D]. 北京： 北京航空航天大学, 2015.

XI K. Virtual flight numerical simulation method and research on dynamic characteristics of vehicle[D]. Beijing, Beihang University, 2015 (in Chinese).

[22]DUPUIS A D, HATHAWAY W. Aeroballistic range tests of the basic finner reference projectile at supersonic velocities: DREV-TM-9703[R]. Valcartier: Defense Research Establishment, 1997.

[23]BHAGWANDIN V A, SAHU J. Numerical prediction of pitch damping stability derivatives for finned projectiles: AIAA-2011-3028[R]. Reston: AIAA, 2011.

黄宇男， 博士研究生。主要研究方向： 计算流体力学、 混合网格数值方法。

Tel: 010-82338071

E-mail: huangyu@buaa.edu.cn

阎超男， 博士， 教授， 博士生导师。主要研究方向： 计算流体力学、 空气动力学。

Tel: 010-82317019

E-mail: yanchao@buaa.edu.cn

Analysis of flying vehicle’s dynamic characteristics based onnumerical virtual flight technology

HUANG Yu1, YAN Chao1,*, XI Ke2, WANG Wen1

1. School of Aeronautic Science and Engineering, Beihang University, Beijing100083, China 2. Institute of Ordnance Industry Navigation and Control Technology, Beijing100089, China

With the numerical virtual flight technology based on structured overlapping grid, closed PID controller, rudder control, rigid body motion and unsteady N-S equation solver, the unsteady motion characteristic, dynamic stability and adjustment of control parameter of Genesis capsule and basic finner projectile have been simulated. The motion characteristic with different degree of freedom (DOF) motion, the motion stability and the adjustment of control parameter with disturbance of those flying vehicles have been analyzed. The calculation results show that the study of flying vehicle’s nonlinear motion under the condition of complex fluid flows can be effectively carried out by numerical virtual flight technology, which has practical value and application prospect in the area of simulation and prediction of flying vehicle’s motion and controlling characteristic, fluid mechanics study and design of control rule under the condition of unsteady and nonlinear aerodynamics.

CFD; overlapping grid; PID control; virtual flight; dynamic derivative; control parameters adjustment; dynamic characteristic; unsteady flow

2016-01-11； Revised： 2016-02-17； Accepted： 2016-04-06； Published online： 2016-04-2015:26

. Tel.： 010-82317019E-mail: yanchao@buaa.edu.cn

2016-01-11； 退修日期： 2016-02-17； 录用日期： 2016-04-06；

时间： 2016-04-2015：26

www.cnki.net/kcms/detail/11.1929.V.20160420.1526.004.html

.Tel.： 010-82317019E-mail:yanchao@buaa.edu.cn

10.7527/S1000-6893.2016.0120

V211.3

A

1000-6893(2016)08-2525-14

引用格式： 黄宇， 阎超， 席柯， 等． 基于数值虚拟飞行技术的飞行器动态特性分析[J]． 航空学报, 2016, 37(8): 2525-2538. HUANG Y, YAN C, XI K, et al. Analysis of flying vehicle’s dynamic characteristics based on numerical virtual flight technology[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2525-2538.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160420.1526.004.html