战斗机垂尾脉动压力数值模拟
2016-11-14孟德虹孙岩王运涛李伟
孟德虹, 孙岩, 王运涛,*, 李伟
1.中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000 2.中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000
战斗机垂尾脉动压力数值模拟
孟德虹1, 孙岩2, 王运涛1,*, 李伟1
1.中国空气动力研究与发展中心 计算空气动力研究所, 绵阳621000 2.中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳621000
在亚跨超计算流体力学(CFD)软件平台(TRIP)上开发了基于RANS/LES混合思路的IDDES流动模拟技术,并通过NACA0021翼型60° 大迎角分离流动与串列圆柱绕流模拟对RANS/LES混合方法的精确度进行了验证,针对某战斗机外形的垂尾脉动压力开展了数值模拟研究。战斗机来流马赫数为0.1,基于全机长度的雷诺数为2×106,模型迎角为20°、30°和40°。分别通过脉动压力系数、脉动压力功率谱密度、空间流动结构以及侧向力响应曲线等对战斗机的垂尾脉动压力进行了分析。脉动压力模拟结果表明:当垂尾完全沉浸在边条翼脱体涡破碎后的宽频湍流脉动气流中时,垂尾翼梢位置的脉动压力会发生明显的增大。
战斗机; 垂尾; 脉动压力; RANS/LES; 计算流体力学(CFD)
为了提高机动性和操纵性,现代高性能战斗机普遍采用边条翼/垂直尾翼的气动布局。大后掠角的边条翼在前缘位置产生高强度的脱体涡,为主机翼上方的气流提供能量,延迟主机翼上的流动分离,提高主机翼的升力。但随着战斗机迎角的增加,边条翼产生的脱体涡会在垂尾前方发生破裂,使战斗机垂尾沉浸在宽频的湍流脉动中,从而诱导垂尾发生抖振[1-2]。垂尾抖振会引起结构疲劳破坏,甚至导致飞行事故发生。战斗机设计前,需要对垂尾抖振边界与抖振响应进行准确预测,避免战斗机在飞行包线内长时间处于抖振区域飞行,提高飞机的安全性能和使用寿命。大量的研究结果表明,垂尾抖振是由边条涡破裂导致的垂尾表面脉动压力引起的。因此,垂尾表面脉动压力的预测是判断抖振起始边界、分析抖振响应特性及研究抖振作用机理的关键[3-4]。
目前,垂尾表面脉动压力预测主要有风洞试验和数值计算两种方法。风洞试验方法[5]通过在垂尾模型表面安装测压孔,获取垂尾表面的脉动压力响应。该方法能够获得物理真实的脉动压力响应特性,但脉动压力测量点数量受限于垂尾模型结构,且空间脉动压力测量困难;另一方面,开展垂尾脉动压力测量风洞试验的时间周期较长、成本较高。数值计算方法通过模拟飞行器绕流下的流场,获取垂尾表面的脉动压力分布。当前,工程应用中通常采用离散求解雷诺平均Navier-Stokes方程RANS(Reynolds Average Navier-Stokes)的方式模拟飞行器的绕流流场,该方法具有计算量小、程序鲁棒性好的特点,但该方法的湍流涡黏性值较大,会快速耗散小尺度高频涡,不利于模拟具有多重尺度的宽频流场结构。因此,传统RANS方法模拟战斗机垂尾表面脉动压力存在一定的局限性。大涡模拟(Large Eddy Simulation, LES)技术具有较好的湍流分辨能力,但计算量过大、壁面边界条件处理困难,尚无法在工程中取得广泛应用。综合RANS和LES优缺点的分离涡模拟(Detached Eddy Simulation, DES)技术成为近十年流动数值模拟领域的研究热点[6-11],并成功应用于大范围分离流动数值模拟[12-15]。
为此,本文在亚跨超CFD计算软件(TRIP)的框架内发展了基于RANS/LES混合方法的模拟技术,通过两个标准算例对RANS/LES混合方法进行了验证。在此基础上,利用RANS/LES混合方法研究了某战斗机模型的垂尾脉动压力特性。
1 数值计算方法
1.1流动控制方程求解
理想气体假设下的非定常N-S方程可以描述为
(1)
式中:Q为守恒变量;Finv为无黏通量;Fvis为黏性通量;Ω为任意封闭域;∂Ω为包围Ω的边界;n为边界位置的法向矢量;t为物理时间。
本文通过有限体积方法离散求解式(1),并基于TRIP软件实现复杂流动的数值模拟。TRIP软件是中国空气动力研究与发展中心自主研发的基于多块结构对接/拼接网格大型通用计算流体力学(ComputationalFluidDynamics,CFD)计算软件,广泛应用于多种工程问题的流动模拟,具有较高的计算精度和数据可信度[16-19]。
本文的数值计算中,式(1)的无黏项离散采用矩阵耗散的中心型差分格式,二阶和四阶人工耗散系数分别取0.000 1和0.01,黏性项离散采用二阶中心格式。非定常计算采用双时间方法进行求解,伪时间步采用隐式方法以提高计算效率。湍流模型包含单方程SA模型[20]与两方程SST模型[21]。采用低速预处理技术、多重网格技术和大规模并行技术提高计算效率。
1.2RANS/LES混合方法
RANS/LES混合方法的思想是在壁面区域采用RANS方法对湍流脉动进行模化,而在分离流动区域利用LES方法分辨多尺度的分离涡。
分离涡模拟方法DES是RANS/LES混合方法的一种典型模式,最早由Spalart[6]等提出,经过十余年的发展,已经形成了多种形式的分离涡模拟技术[7-8,10]。其中,Shur[10]等发展的IDDES(ImprovedDelayedDES)具有DDES模型与壁面LES模型的双重优点,能够解决边界层附近“Log-LayerMismatch”的问题,且能实现分离区中RANS到LES的快速转换。本文采用的RANS/LES混合方法是在SST湍流模型基础上发展的IDDES流动模拟技术。
SST湍流模型的控制方程可以表示为
(2)
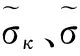
(3)
式中:常数β*为0.09。
将式(2)中的湍流长度尺度LRANS替换为大涡模拟的滤波尺度LLES,则式(2)转变为两方程的大涡模拟控制方程。通过选择长度尺度混合方式,可以得到不同的RANS/LES混合方法。IDDES方法的长度尺度LIDDES定义为
(4)
(5)
其中:CDES为DES经验参数,取值为0.65,其他系数和变量的定义分别为
(6)
式中:dw为壁面距离;Δmax为网格单元最大尺度;Δwn为壁面网格单元法向高度;Δ为网格长度尺度;常数Cw为0.15;常数ct为1.87;常数cl为5.0;rdt、rdl分别为rd的湍流和层流分量,定义为
(7)
式中:νt、νl分别为湍流与层流运动黏性系数;ui为流动速度分量;xj为空间坐标分量;常数κ为0.41。
2 数值方法验证
本节通过NACA0021翼型与串列圆柱两个分离流标准算例对本文选择的RANS/LES混合方法进行验证。
2.1NACA0021翼型绕流
NACA0021翼型大攻角绕流计算是欧盟DES标准算例之一。该算例计算条件为,来流Ma为0.1,基于弦长的雷诺数Re为270 000,翼型迎角α为60°。计算网格采用DESider官方网站提供的网格,图1给出了展向剖面的网格,单个剖面网格单元数量为21 400,展向网格的尺度为0.025c,分别计算了展向长度Lz为c、2c和4c时的绕流流场,对应的展向网格节点数量分别为41、81和161。

图1 NACA0021翼型流场计算网格(X-Y截面)Fig.1 Flow field computational grid of NACA0021airfoil (X-Y section)
图2 NACA0021翼型压力系数分布Fig.2 Pressure coefficient distribution of NACA0021 airfoil
图2给出了不同展向长度下NACA0021翼型的时均压力系数分布曲线与试验结果的对比。其中,压力系数采样点为中间展向位置的网格点。可以看出,展向长度值对下翼面压力系数分布影响很小,不同展向长度的下翼面压力系数与试验值吻合较好,但对于上翼面压力系数分布,展向长度的影响明显。由于上翼面处于大的分离区内,上翼面压力趋向于一致,表现为一个明显的压力平台区。展向长度Lz等于弦长c时,本文计算得到压力平台区存在一定的波动,与试验结果存在明显的差异;当Lz=2c时,计算得到的上翼面压力平台区明显,并与试验结果比较接近;当模型展向长度继续增加,如Lz=4c时,压力平台区也比较明显,但计算数据与试验结果之间的差异在逐渐增大。
图3给出了展向长度Lz=2c时NACA0021翼型阻力系数功率谱密度计算结果与试验数据的对比,其中横坐标St为斯特劳哈数。可以看出,本文计算结果较好地分辨出了前后缘分离涡脱落的主频率。
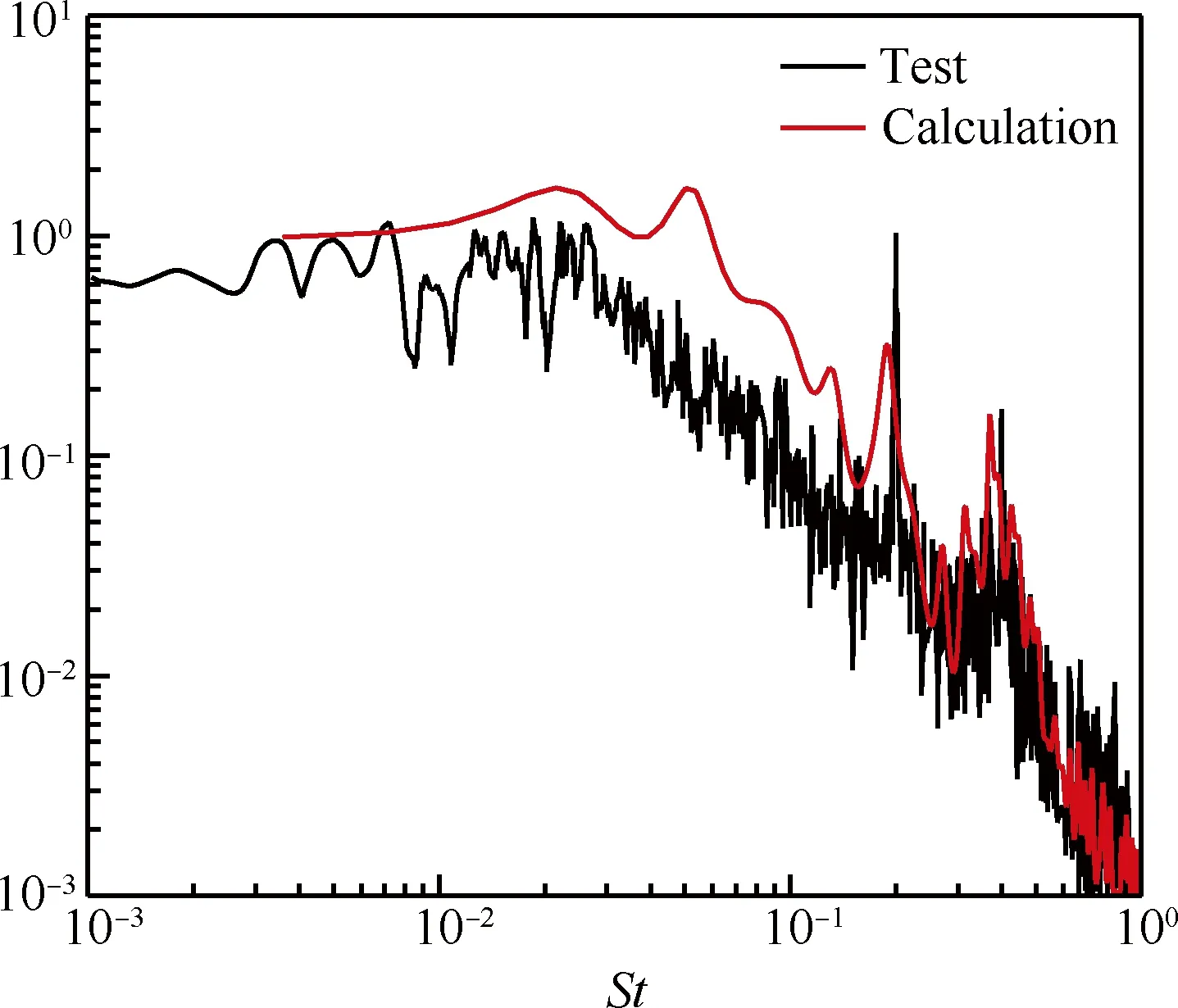
图3 NACA0021翼型阻力系数功率谱密度曲线(Lz=2c)Fig.3 Power spectrum density curves of drag coefficients of NACA0021 airfoil (Lz=2c)
2.2串列圆柱
串列圆柱大范围分离流动是欧盟ATAAC项目与美国AIAABANC项目的标准算例之一。该算例计算条件为,来流速度U为44m/s,基于圆柱直径D的雷诺数ReD为166 000,两个圆柱轴之间的距离L为圆柱直径的3.7倍。本文计算网格采用ATAAC提供的标准网格,图4给出了该网格的X-Y截面网格分布。X-Y截面网格单元数量约为80 000,圆柱展向长度Lz取圆柱直径D的3.0倍,展向网格尺度取0.02D,展向共有151个网格点。

图4 串列圆柱计算网格(X-Y截面) Fig.4 Computational grid of tandem cylinders(X-Y section)
图5给出了串列圆柱前后圆柱时均压力系数分布曲线与试验结果的对比,其中横坐标θ为圆柱表面点的方位角。从图中可以看出,计算的串列圆柱压力系数分布与风洞试验结果基本吻合。
图6给出了后圆柱给定位置点(θ=45°)的压力系数脉动功率谱密度曲线计算与试验结果的对比,其中横坐标f为频率。可以看出,本文计算方法较好地捕捉到了后圆柱分离涡脱落的主频率。
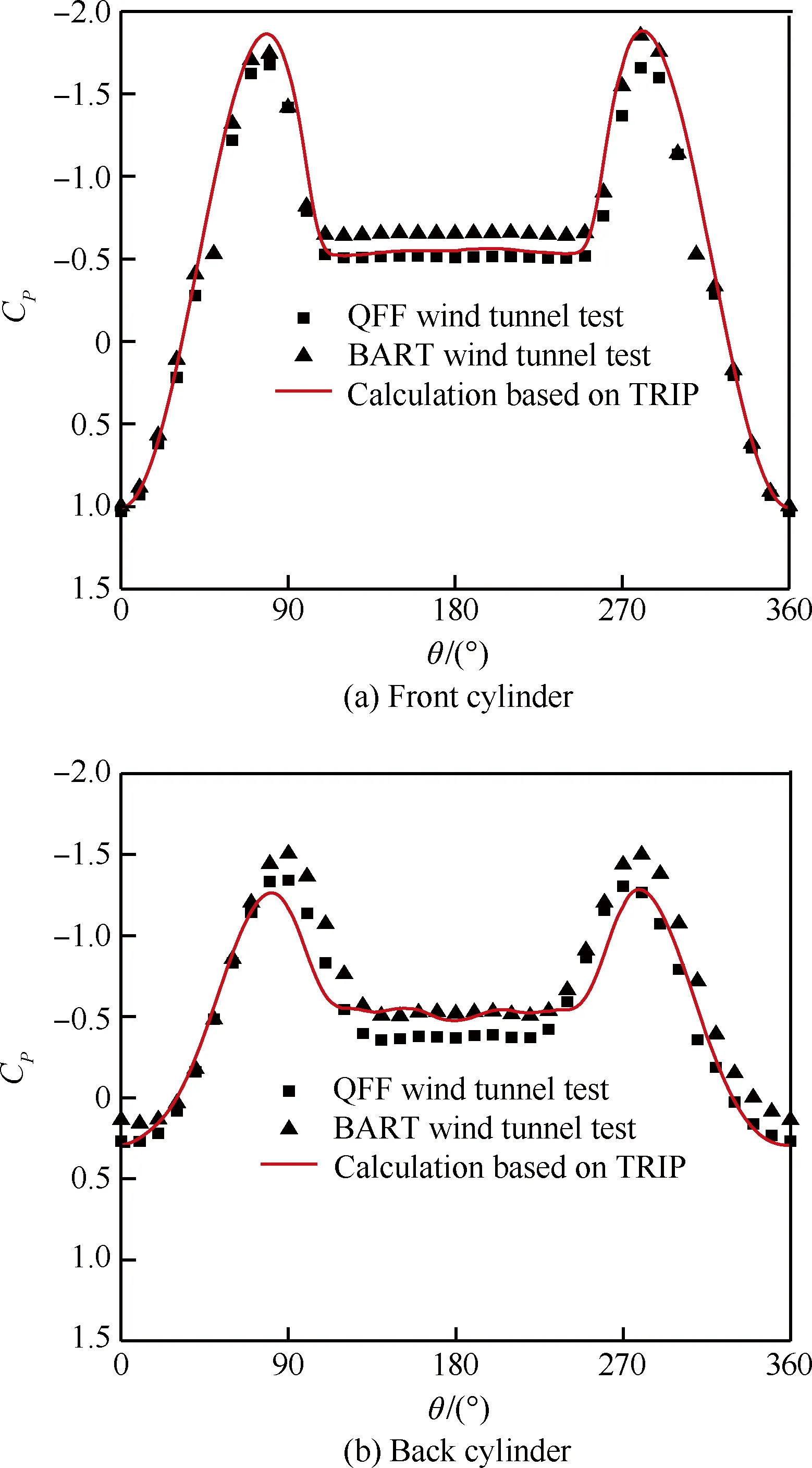
图5 串列圆柱压力系数分布Fig.5 Pressure coefficient distribution of tandem cylinders

图6 串列圆柱功率谱密度曲线Fig.6 Power spectrum density curves of tandem cylinders
3 垂尾脉动压力计算
利用前面经过验证的RANS/LES混合计算方法,本节开展了某战斗机风洞模型垂尾脉动压力特性的计算研究。图7给出了该战斗机模型的外形,该模型在机翼前方有一个大后掠的边条,与战斗机的进气道融合在一起,机翼尾部上方有两个垂直尾翼。该模型在中国空气动力研究与发展中心低速所进行了常规测力试验,模型进气道和尾喷管进行了封堵处理,没有考虑进气道流动对模型绕流的影响。

图7 战斗机模型外形Fig.7 Shape of fighter model
3.1计算网格与计算参数
图8给出了该战斗机模型的流场计算网格。该网格为多块结构对接网格,包含310个网格块、31 610 240个网格单元,第一层网格距离为5.0×10-6,对应的网格y+约为1.0。来流马赫数Ma为0.1,基于模型全机长度的雷诺数Re为2.0×106。根据Spalart的估算,DES采用计算网格需要达到107量级,本文计算网格规模达到DES计算的网格数量要求。网格计算域的最大范围为战斗机平均气动弦长的100倍左右,在战斗机背风面分离区域进行加密,最小的网格尺度小于平均气动弦长的0.5%,并且在分离流动区域,尽量使得网格各向同性(即Δx≈Δy≈Δz)。无量纲非定常计算时间步长Δt取0.004,保证每个流动周期内不少于100个迭代步。模型迎角α取20°、30°和40° 三个角度。

图8 战斗机模型计算网格Fig.8 Computational grid of fighter model
3.2垂尾脉动压力特性
图9给出了不同机身迎角下的全机等Q值图。可以看出,随着机身迎角的增加,边条翼形成的脱体涡在加速破裂,机身迎角为20° 时,边条翼脱体涡一直延伸到垂尾的弦向中部位置才发生破裂,垂尾主要受脱体涡的影响;机身迎角为30° 时,边条翼脱体涡在垂尾前附近发生破裂,整个垂尾沉浸在破裂后的小涡结构中;机身迎角为40° 时,边条翼脱体涡在主机翼前缘位置附近就发生破裂,破裂后的小涡结构沿着流向运动,到达垂尾时,靠近垂尾翼梢位置的小涡结构被衰减掉许多。由图9基于等Q值图显示的空间流场涡结构可以分析出,机身迎角为30° 时,垂尾可能产生较大的抖振响应。

图9 等Q值图Fig.9 Contour of Q value
图10给出了左垂尾外翼面(靠近机翼翼梢方向)脉动压力系数CPrms分布云图,脉动压力系数通过脉动压力均方根值定义得到。从图10中可以看出,垂尾前缘的压力脉动要高于后缘位置的压力脉动值,说明沿着气流运动的方向(X方向),湍流脉动是在逐步衰减的。当模型迎角α为20° 时,垂尾翼根前缘附近的压力脉动较大,而翼梢、翼根后缘位置附近的压力脉动接近零,如图10(a),说明此时边条翼形成的脱体涡在垂尾前缘还保持大涡状态,脱体涡离机翼上翼面距离较近,脱体涡在垂尾1/2弦线位置附近发生破裂后仅对翼根的脉动压力产生了影响;当模型迎角α为30° 时,垂尾翼根和翼梢前缘位置均出现较大的压力脉动,而翼梢后缘位置的压力脉动值也较大,如图10(b),说明边条翼形成的脱体涡在机翼前缘附近发生了破裂,整个垂尾沉浸在脱体涡破裂后的宽频湍流脉动气流中;当模型迎角α为40° 时,垂尾翼根前缘附近压力脉动高于其他位置,而翼梢、翼根后缘位置的压力脉动值均不是很大,如图10(c),说明边条翼形成的脱体涡在垂尾较前位置已经发生了破裂,破裂后的脱体涡对垂尾翼根前缘附近的压力脉动产生了影响,而垂尾大部分位置,尤其是垂尾翼梢处于充分发展的宽频湍流气流中,脉动压力值相对机身迎角为30° 时有所降低。

图10 垂尾脉动压力系数分布云图Fig.10 Contour of fluctuating pressure coefficient distribution on vertical tail
为了更好地比较不同机身迎角下的垂尾压力脉动值差异,在垂尾外翼表面翼根、翼中和翼梢位置选择了3条监测线,每条监测线上均匀分布9个点,如图11所示。

图11 垂尾脉动压力监测点位置Fig.11 Monitoring point location of fluctuating pressure of vertical tail
图12给出了垂尾不同监测点的脉动压力系数分布。可以看出,不同机身迎角下翼根位置(Line1)和翼中位置(Line2)的脉动压力系数分布差异并不明显,而对于翼梢位置(Line3),机身迎角变化对脉动压力系数影响很大,机身迎角30° 时翼梢位置(Line3)的压力脉动要明显大于迎角20° 和40° 时的压力脉动。翼梢位置的压力脉动耦合力臂效应,会在垂尾翼根部位形成较大的弯曲力矩,使得垂尾发生疲劳破坏,因此,需要避免翼梢位置产生较大的脉动压力。图12的结果再次验证了前面关于不同机身迎角下垂尾脉动压力系数分布的论述。

图12 监测点脉动压力系数分布Fig.12 Fluctuating pressure coefficient distribution of monitoring points
图13给出了不同机身迎角下监测点1位置脉动压力的功率谱密度曲线,监测点1的位置如图11所示,为垂尾翼根靠近前缘的一个点。从图13 可以看出,机身迎角为20° 时,监测点1位置脉动压力功率谱密度曲线存在一个峰值,对应图9关于流场涡结构的分析,该脉动峰值应是由边条翼形成的脱体涡引起的,脉动峰值对应的频率为边条翼脱体涡脱落的频率,约为380Hz;而当机身迎角为30°、40° 时,脱体涡在垂尾前方已经发生了破裂,因此,监测点1位置对应的脉动压力功率谱密度曲线表现为宽频模式,没有明显的脉动峰值,如图13所示。
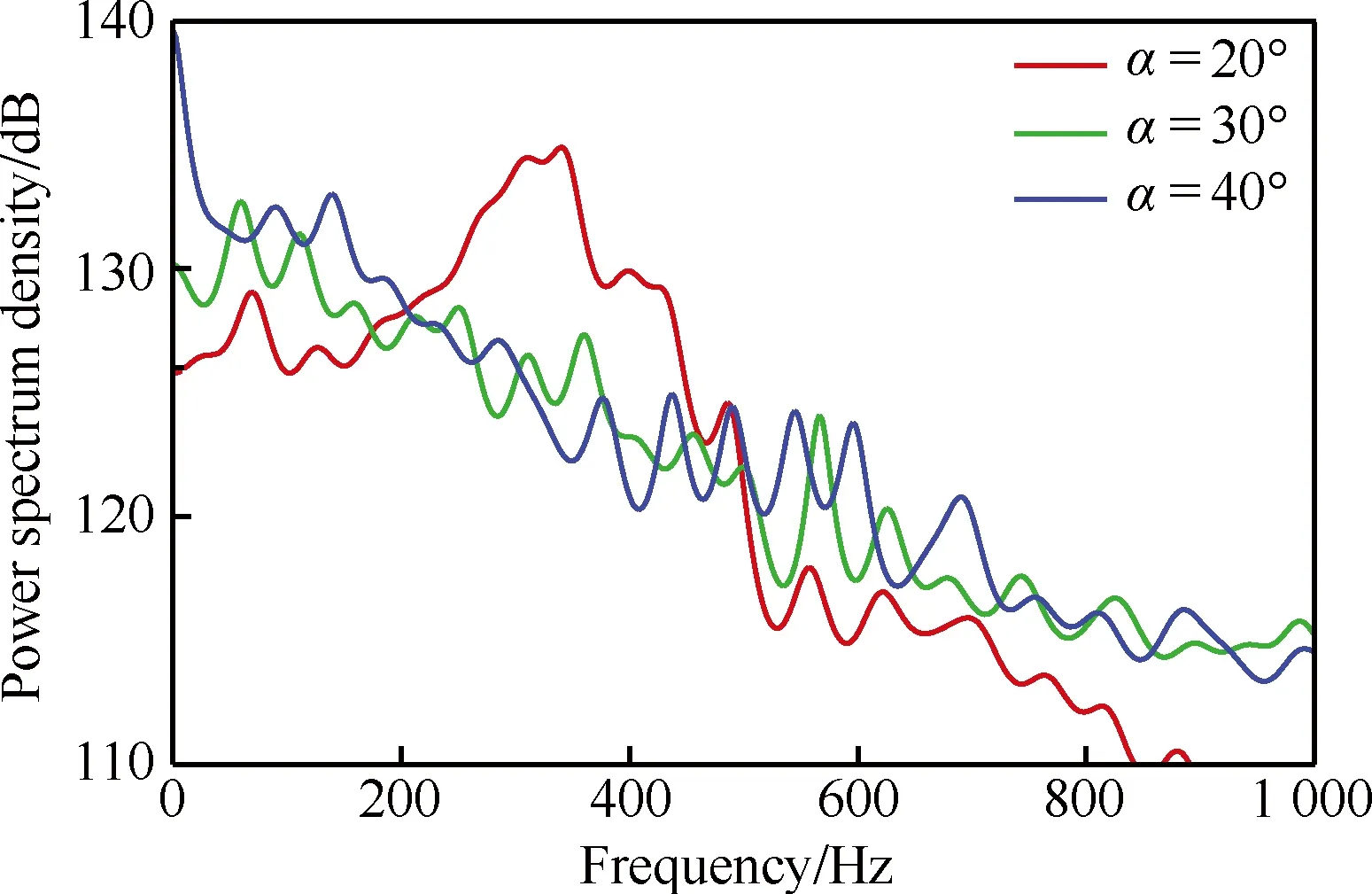
图13 监测点1脉动压力的功率谱密度曲线Fig.13 Power spectrum density curves of fluctuating pressure of monitoring point 1
图14给出了非定常RANS/LES混合方法计算的垂尾侧向力系数CC的时间响应曲线。

图14 垂尾侧向力系数响应曲线Fig.14 Side force coefficient response curves of vertical tail
可以看出,3个机身迎角下,RANS/LES混合方法能够比较好地模拟出垂尾侧向力的响应特性。从模拟结果可以看出,随着机身迎角增加,垂尾的侧向力的绝对值在减小,但侧向力的脉动水平在增长。
为了更详细地比较侧向力的脉动差异,图15给出了不同机身迎角下的垂尾侧向力系数功率谱密度曲线。可以看出,在低频区域,随着机身迎角的增加,垂尾侧向力脉动在增大;在高频区域,机身迎角30° 的垂尾侧向力脉动由于小涡结构在垂尾部分的耗散而与机身迎角20° 时的垂尾侧向力脉动相当,而机身迎角为40° 时,小涡结构在到达垂尾区域已经被耗散,因此,此时的垂尾侧向力脉动要低于机身迎角为20°、30° 时的垂尾侧向力脉动。
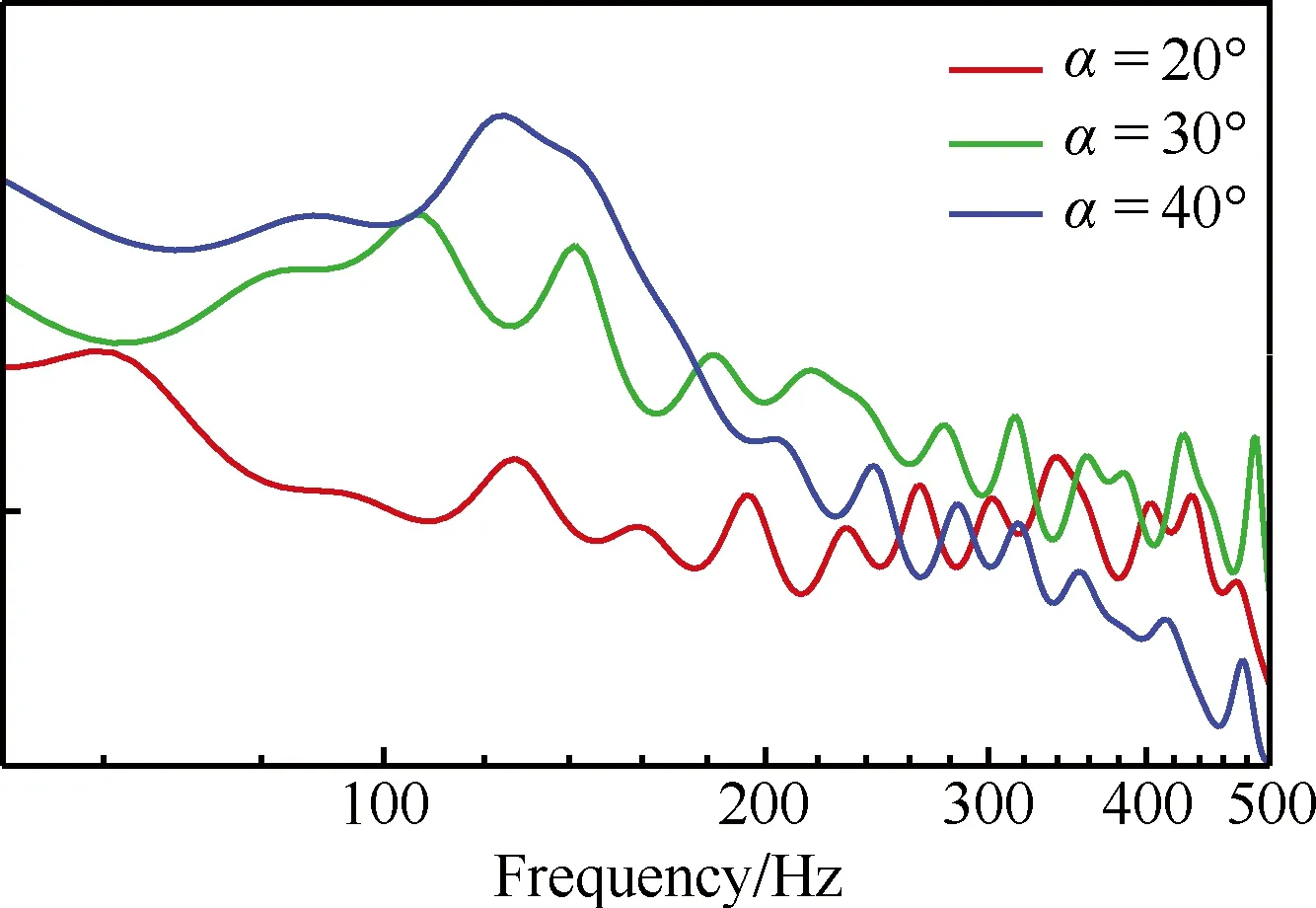
图15 垂尾侧向力系数功率谱密度曲线Fig.15 Power spectrum density curves of side force coefficient of vertical tail
由图15可以看出,机身迎角30° 和40° 时,垂尾侧向力的低频脉动量相当,这是由于侧向力是整个垂尾的积分力,从图10垂尾脉动压力系数分布可以看出,机身迎角40° 时翼根位置的脉动压力要高于30° 时的脉动压力,翼梢位置则相反。虽然机身迎角30° 和40° 时垂尾侧向力的低频脉动量相当,但翼梢位置的压力脉动会引起更大的垂尾抖振响应。
4 结 论
在亚跨超CFD软件平台(TRIP)的框架内,发展了基于RANS/LES混合方法的流动模拟技术,通过NACA0021翼型大迎角分离流动和串列双圆柱绕流算例对RANS/LES混合方法的模拟精度进行了验证,并在此基础研究了某战斗机模型在大迎角状态下的垂尾脉动压力。从数值模拟结果可以得到以下结论:
不同迎角下垂尾脉动压力差异主要体现在翼梢位置,当机身迎角达到一定值时,垂尾完全沉浸在脱体涡破裂后的宽频湍流脉动中,翼梢位置的脉动压力较明显,当机身迎角较小时,脱体涡靠近主机翼,翼梢位置没有破碎的脱体涡,而当机身迎角较大时,翼梢位置的破碎脱体涡被充分衰减。
[1]贾有, 杨智春. 一种飞机垂尾抖振载荷识别的新方法[J]. 航空学报, 2013, 34(10): 2333-2340.
JIA Y, YANG Z C. A new approach to identify buffet loads for aircraft vertical tail[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(10): 2333-2340 (in Chinese).
[2]韩冰, 徐敏, 蔡天星, 等. 涡破裂诱导的垂尾抖振数值模拟[J]. 航空学报, 2012, 33(5): 788-795.
HAN B, XU M, CAI T X, et al. Numerical simulation of vertical tail buffeting induced by vortex breakdown[J]. Acta Aeronautica et Astronautica Sinica, 2012, 32(5): 788-795 (in Chinese).
[3]HUANG J T, GAO Z H. Buffeting numerical simulation coupled with aerodynamics and structure based on MDDES[J]. Science China Technological Sciences, 2013, 56: 1550-1560.
[4]AHMED E, OSAMA A K, OKTAY B. F/A-18 twin-tail buffet modeling using non-linear eddy viscosity models: AIAA-2014-2447[R]. Reston: AIAA, 2014.
[5]李劲杰, 杨青, 杨永年, 等. 边条翼布局双垂尾抖振表面压力脉动风洞实验研究[J]. 实验流体力学, 2006, 20(3): 29-32.
LI J J, YANG Q, YANG Y N, et al. Wind-tunnel unsteady pressure measurements of twin-vertical tail during buffet of strake-wing configuration[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(3): 29-32 (in Chinese).
[6]SPALART P R, JOU W H, STRETLETS M, et al. Comments on the feasibility of LES for wings and on the hybrid RANS/LES approach[C]//Proceedings of the First AFOSR International Conference on DNS/LES. Colombus: Greyden Press, 1998: 137-147.
[7]DECK S. Zonal-detached-eddy simulation of the flow around a high-lift configuration[J]. AIAA Journal, 2005, 43(11): 2372-2384.
[8]SPALART P R, DECK S, SHUR M, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theory and Computation Fluid Dynamics, 2006, 20(3): 181-195.
[9]SPALART P R. Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41(1): 181-202.
[10]SHUR MIKHAIL L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649.
[11]MIKHAIL S G, ANDREY V G, JOCHEN S, et al. Development of DDES and IDDES formulations for thek-ωshear stress tranport model[J]. Flow Turbulence Combust, 2012, 88(3): 431-449.
[12]DECK S. Numerical simulation of transonic buffet over a supercritical airfoil[J]. AIAA Journal, 2005, 43(7): 1556-1566.
[13]吴晶峰, 宁方飞. 后台阶流动的Hybrid RANS/LES模拟[J]. 北京航空航天大学学报, 2011, 37(6): 701-704.
WU J F, NING F F. Hybrid RANS-LES method applied to backward facing step flow[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(6): 701-704 (in Chinese).
[14]XIAO Z X, LIU J, LUO K Y, et al. Numerical investigations of massively separated flows past rudimentary landing gear using SST-DDES: AIAA-2012-0385[R]. Reston: AIAA, 2012.
[15]HUANG J B, XIAO Z X, LIU J, et al. Simulation of shock wave buffet and its suppression on an OAT15A supercritical airfoil by IDDES[J]. Science China: Physics, Mechanics and Astronomy, 2012, 55(2): 260-271.
[16]王运涛, 王光学, 张玉伦. TRIP2.0软件的确认: DPWII复杂组合体的数值模拟[J]. 航空学报, 2008, 29(1): 34-40.
WANG Y T, WANG G X, ZHANG Y L. Validation of TRIP2.0: Numerical simulation of DPWII complex configuration[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(1): 34-40 (in Chinese).
[17]王运涛, 王光学, 张玉伦. 采用TRIP2.0软件计算DLR-F6构型的阻力[J]. 空气动力学学报, 2009, 27(1): 108-113.
WANG Y T, WANG G X, ZHANG Y L. Drag prediction of DLR-F6 configuration with TRIP2.0 software[J]. Acta Aerodynamica Sinica, 2009, 27(1): 108-113 (in Chinese).
[18]王运涛, 王光学, 张玉伦. DPWIII机翼和翼身组合体构型数值模拟[J]. 空气动力学学报, 2011, 29(3): 264-269.
WANG Y T, WANG G X, ZHANG Y L. Numerical simulation of DPW III wing and wing-body configurations[J]. Acta Aerodynamica Sinica, 2011, 29(3): 264-269 (in Chinese).
[19]王运涛, 张书俊, 孟德虹. DPW4翼/身/平尾组合体的数值模拟[J]. 空气动力学学报, 2013, 31(6): 739-744.
WANG Y T, ZHANG S J, MENG D H. Numerical simulation and study for DPW4 wing/body/tail[J]. Acta Aerodynamica Sinica, 2013, 31(6): 739-744 (in Chinese).
[20]SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows: AIAA-1992-0439[R]. Reston: AIAA, 1992.
[21]MENTER F R. Two equation eddy viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605.
孟德虹男, 硕士, 助理研究员。主要研究方向: 计算空气动力学。
Tel: 0816-2463274
E-mail: mdh157@163.com
孙岩男, 博士研究生, 助理研究员。主要研究方向: 计算气动弹性力学。
Tel: 0816-2463205
E-mail: supersunyan@163.com
王运涛男, 博士, 研究员, 博士生导师。主要研究方向: 计算空气动力学。
Tel: 0816-2463015
E-mail: ytwang@skla.cardc.cn
李伟男, 博士研究生, 助理研究员。主要研究方向: 计算空气动力学。
Tel:0816-2463274
E-mail: kuaile06@163.com
Numerical simulation of fluctuating pressure of fighter vertical tail
MENG Dehong1, SUN Yan2, WANG Yuntao1,*, LI Wei1
1. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center,Mianyang621000, China 2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center,Mianyang621000, China
IDDES flow simulation technique based on hybrid RANS/LES method is realized on TRIP, a trisonic fluid simulation software platform. Separating flows around airfoil NACA0021 with 60° angle of attack and tandem cylinders are simulated to validate the precision of hybrid RANS/LES method. Then, fluctuating pressure of a fighter vertical tail is calculated with the presented RANS/LES method. Flow Mach number is 0.1, Reynolds number based on length of fighter is 2 million, and angles of attack are 20°, 30° and 40°. Fluctuating pressure of fighter vertical tail is analyzed through fluctuating pressure coefficients, power spectrum density of fluctuating pressure, space flow structure and side force response. Numerical results show that fluctuating pressure on tip of vertical tail increases obviously when vertical tail is immersed in broadband turbulence fluctuating flow behind the breakup of separating vortex from strake wing.
fighter; vertical tail; fluctuating pressure; RANS/LES; computational fluid dynamics (CFD)
2016-01-18; Revised: 2016-01-23; Accepted: 2016-04-11; Published online: 2016-04-2616:02
National Key Research and Development Plan (2016YFB0200700)
. Tel.: 0816-2463015E-mail: ytwang@skla.cardc.cn
2016-01-18; 退修日期: 2016-01-23; 录用日期: 2016-04-11;
时间: 2016-04-2616:02
www.cnki.net/kcms/detail/11.1929.V.20160426.1602.002.html
国家重点研发计划 (2016YFB0200700)
.Tel.: 0816-2463015E-mail: ytwang@skla.cardc.cn
10.7527/S1000-6893.2016.0121
V211.3
A
1000-6893(2016)08-2472-09
引用格式: 孟德虹, 孙岩, 王运涛, 等. 战斗机垂尾脉动压力数值模拟[J]. 航空学报, 2016, 37(8): 2472-2480. MENG D H, SUN Y, WANG Y T, et al. Numerical simulation of fluctuating pressure of fighter vertical tail[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2472-2480.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
URL: www.cnki.net/kcms/detail/11.1929.V.20160426.1602.002.html
