铁路既有曲线整正计算方法研究

2010-07-30刘永孝张咏军

铁道建筑 2010年11期

刘永孝，张咏军

(兰州交通大学土木工程学院，兰州 730070)

在既有线平面改建及日常线路的大、中维修中，多根据外业测得的曲线正矢、偏角及测点坐标来确定使该曲线保持圆顺所需要的曲线半径、缓和曲线长度，进而计算出各计算点的拨道量[1]。

铁路曲线整正常用的计算方法有三种，即偏角法、绳正法、坐标法。其中偏角法和绳正法是基于渐伸线原理进行计算的，计算结果有一定的近似性，对外业施测和内业计算有相应要求，在一定条件下是满足测量和计算精度要求的[2]。而坐标法具有理论严密、公式推求准确、测量计算成果精度高等优点[3]。

在这些拨道计算方法中，以往都是将它们独自分隔开来，并且分析渐伸线误差及适用范围时，都采用了理论分析方法，很少针对实测数据进行对比研究。本文针对同一条曲线，选用相同的曲线参数，将这三种方法结合起来，研究它们之间的转化公式，计算出各自的拨量值，同时将它们的计算结果进行对比，分析出利用渐伸线整正曲线的误差大小及规律。

1 曲线整正计算方法间的转化关系分析

1.1 偏角法转坐标法

如图1所示γi－1=180°－ (βi－1－ αi－1)

根据余弦定理有

式中 αi——i测点的累计偏角;

βi－1——i－1 测点与后一测点 i的 20 m 的弦与水平线形成的夹角;

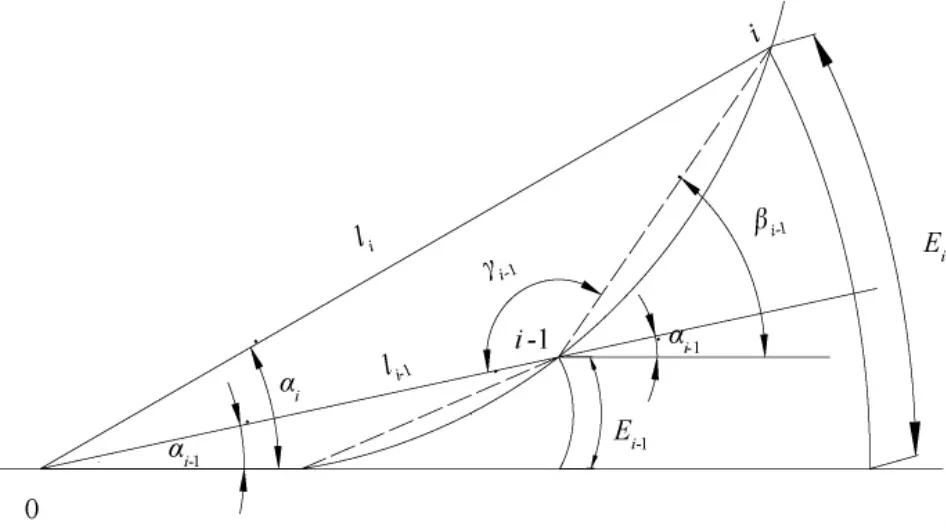
图1 曲线计算示意

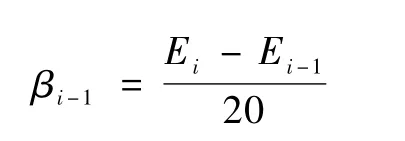
Ei——i点的渐伸线长度;

γi－1——i－1 点的视距线与 i－1 测点与后一测点i的20 m的弦线间的夹角;

li——各计算点与置镜点的距离，也就是视距。

则有 xi=licosαiyi=lisinαi

xi，yi为各计算点转化坐标法下的坐标。

如果置镜点转变，则置镜点后的坐标用公式

xn+i=xn+licosαi

yn+i=yn+lisinαi

式中，xn，yn为置镜点的坐标。

1.2 偏角法转正矢法

利用渐伸线原理计算拨量采用下面公式

en=En－ E′n

式中 en——计算点的拨量;

En——计算点的既有渐伸线长度;

E′n——计算点的设计渐伸线长度。

根据渐伸线的特性，渐伸线E可以近似地用逐渐加大半径的累积圆弧段来表示[4]。

各测点相应的渐伸线长度为:E1，E2，E3，…，En，参照图2所示计算

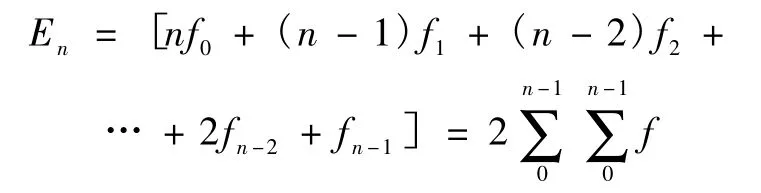
图2 渐伸线长度示意

由上式可以得出:第n点的渐伸线长度E′n等于到前一点(n－1)为止的正矢累计的合计数的两倍。

同理，对于正矢为计划正矢 f′的曲线上 n点的渐伸线长度为

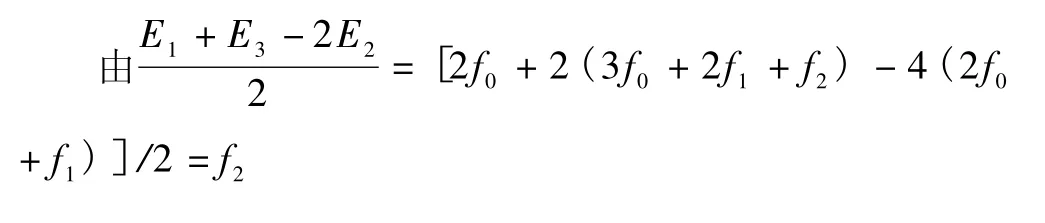
同理得拨后正矢

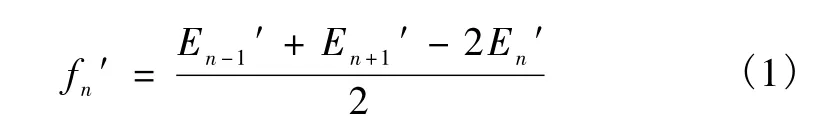
1.3 坐标法转正矢法

第i点的坐标为(xi，yi)，第 i+1点的坐标为(xi+1，yi+1)

则i点的现场正矢为

第i点的拨后正矢为

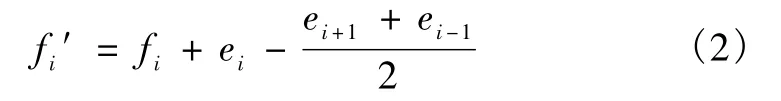
2 实际应用

2.1 偏角法和坐标法计算拨距分析

图3 0<α<1时偏角法与坐标法分析数据对比

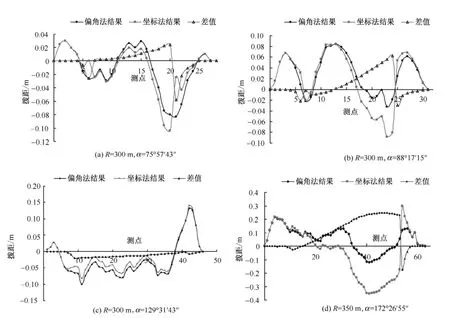
图4 1<α<π时偏角法与坐标法分析数据对比

图5 α>π时偏角法与坐标法分析数据对比

利用偏角法所测曲线的数据，先根据偏角法进行优化得出优化半径和缓和曲线长度，再计算出拨距。然后利用1.1所述公式将其转化为坐标法进行计算，在对坐标法进行计算时，取和偏角法优化所取的相同的参数(半径，缓和曲线长度)，算得坐标法拨距。将偏角法计算拨距结果和坐标法计算结果进行对比分析。上述计算都是通过FORTRAN编程进行，通过对现场实测的大量数据分析，可看出一些规律。现选取其中一些有代表性的曲线拨距分析结果如图3、图4、图5所示。

从图3可以看出当偏角0<α<1弧度时，利用渐伸线结果算出的拨距和坐标法算出的结果很接近，这说明当偏角小于1弧度时，利用渐伸线算出的拨距结果误差很小。通过对大量数据分析其误差最大不超过30 mm，并且随着偏角的增大，其误差也随着增大。

从图4可以看出，当偏角1<α<π弧度时，利用渐伸线结果算出的拨距和坐标法算出的结果相差较大，这说明当偏角大于1弧度，小于2弧度时，利用渐伸线算出的拨距结果误差较大。通过对大量数据分析其误差最大可达到200 mm，并且随着偏角的增大，其误差也跟着增大。

从图5可以看出当偏角α>π弧度时，利用渐伸线结果算出的拨距和坐标法算出的结果相差很大，这说明当偏角大于π弧度时，利用渐伸线算出的拨距结果误差很大。通过对大量数据分析其误差最大可达到1 000 mm，并且随着偏角的增大，其误差也跟着增大[5]。

2.2 坐标法和偏角法拨后正矢分析

对同一曲线，采用相同的曲线要素，分别用偏角法和坐标法计算其拨距，然后通过公式(1)可算出偏角法的拨后正矢，用公式(2)可计算出坐标法对应的拨后正矢。因坐标法计算出的拨后正矢是精确的，可将偏角法计算出的结果和坐标法计算出的结果进行对比分析，并可计算出偏角法的拨后正矢误差。通过对大量的数据分析，现取两个转角比较大的曲线分析如图6所示。

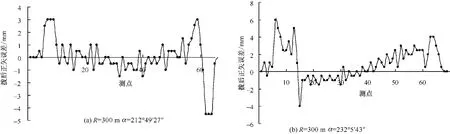
图6 偏角法拨后正矢误差分析

2.3 讨论

通过对大量的数据分析对比，可发现当偏角小于1弧度时，虽然两种方法计算出的拨距稍有差别，但是其拨后正矢几乎是相等的，只有个别点有误差，但误差不超过1 mm。当偏角大于1弧度小于π时，两种方法计算出的拨量相差较大，但其拨后正矢只有一些点有差别，但差值都不超过1 mm。当偏角大于π时，两种方法计算出的拨量相差很大，其拨后正矢的差值也较大，差值最大达到了6 mm。实际上这些差值也就是利用渐伸线原理计算产生的误差。