面向复杂构型飞机的非定常气动力建模与辨识

杨文， 卜忱， 眭建军， 尚祖铭

中航工业空气动力研究院 气动发展部， 哈尔滨　150001



面向复杂构型飞机的非定常气动力建模与辨识

杨文， 卜忱*， 眭建军， 尚祖铭

中航工业空气动力研究院 气动发展部， 哈尔滨150001

不论是现代高机动隐身战斗机的设计需求还是常规布局飞机的飞行动力学分析，深入研究大迎角飞行时的非线性非定常气动力模型都极其重要。基于纵向运动小振幅及大振幅强迫振荡试验数据，分析了常规稳定导数模型的准确性，并从导数模型出发发展了简化涡流和分离流时间迟滞效应的非定常气动力线性模型和非线性模型，最后应用风洞典型机动历程模拟试验验证了模型的有效性。结果表明：对于复杂构型高机动飞机模型，发展并改进的非线性微分方程模型可以准确预测飞机不同机动下的非定常气动力特性，具有较强的工程可行性。

大迎角； 非定常气动力； 时间迟滞； 微分方程； 典型机动

在大气飞行力学中，确定并描述作用在飞机上的气动力及力矩是一项非常重要的任务，而将飞行力学与其他力学分支区分开来的正是其中的气动力部分。严格地来讲，气动力及力矩都是飞行状态变量的泛函。大量的试验结果表明[1-3]，他们不仅仅与这些飞行状态变量的瞬时值有关，还与这些变量在运动过程中的整个时间历程相关。实际应用中，仅采用这些变量及其导数的函数表征气动力及力矩，并拓展至关于这些变量的泰勒展开式。然而，如果将来要配备有多重控制器并具备大迎角区域、高机动性的战斗机，那么在飞行动力学分析及控制律设计中，就要求足够准确的非定常气动力模型。即使对于正常布局的飞机，在其大迎角飞行条件下准确预测其非定常气动力也是非常必要的。

相对于数值模拟方法，基于风洞试验数据建立非定常气动力模型仍然是目前非定常气动力建模研究的主要手段。目前大迎角非定常气动力建模方法中国内外研究最多的主要有两大类：一类是基于飞机表面流动机理确定的非定常气动力和运动状态变量的数学关系表达式，如稳定导数模型[4]及其扩展的多项式模型[5]、阶跃响应函数模型[6-7]及其简化模型[8]、状态空间模型[9-11]和非线性微分方程模型[12-14]等；另一类是避开复杂的物理机理直接采用诸如模糊逻辑[15-16]、神经网络[17]及模糊神经[18]等纯数学的方法进行非线性代数拟合建模。

然而，目前在实际的飞行动力学分析及飞行控制工程应用中仍然采用稳定导数模型，而上述关于气动力建模的研究还主要是集中在方法上，很少有人评价传统导数模型表达式的准确性，更谈不上在此基础上发展大迎角非定常气动力模型。其次，许多建模方法的介绍中，仅仅涉及到诸如大后掠三角翼等布局的气动力建模研究，而且很少应用机动历程试验验证模型的有效性。实际的研究发现，在工程中小展弦比复杂构型飞机的气动力建模通常需要对模型结构进行修正并对辨识算法进行改进。本文[12]基于Goman提出的微分方程模型基本结构形式，从分析常规稳定导数模型的准确性出发，发展并改进了同时适用于某小展弦比复杂构型动态标模小振幅和大振幅运动的非定常气动力微分方程模型，最后应用在FL-8低速风洞中完成的尾冲机动[19]模拟试验验证非线性微分方程模型的有效性和适用性。

1　稳定导数模型

尽管动导数与频率相关性很强，但在实际应用中，大迎角区域的气动力模型仍然沿用式(1)所表达的常规导数模型:

Ciδ(α,ω)δ

(1)

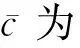
模型中导数与频率的相关性使其与时间域的气动力建模任务不一致。在实际的稳定性分析及飞行仿真中，式(1)中的频率相关性往往被忽略。结果，减缩频率ω随意选取可能就会导致气动力导数模型具有极大地不确定性。图1给出了小振幅俯仰振荡法向力系数CN迟滞环和导数模型的对比图，其中f表征频率。可以看出在失速迎角附近区域，模型预测和试验结果存在较大差别。

图1　导数模型与试验数据的比较(f=1.0 Hz)Fig.1　Comparison between derivatives model and test data (f=1.0 Hz)

2　线性微分方程模型

2.1模型表达式推导

针对第1节中导数模型遇到的问题，基于机翼表面流动机理[11]，Goman等提出了一种单自由度俯仰小幅振荡线性微分方程模型[12]，具体表达式为

对于小振幅强迫振荡试验，迎角的变化规律为

Ci(t)=Ci0+Ciααssin ω t+Ciqαsω cos ω t

(4)

式中：Ci0为气动力均值；Ci α和Ci q分别为所谓的“同相”及“异相”气动力导数，并且在大迎角时与频率、振幅相关。

将式(3)代入气动力模型式(2)中，经拉普拉斯变换、线性化、拉普拉斯反变换及归并同类项后，与式(4)中同相及正交动导数比较，整理可得

(5)

式中：ΔCiα,vb=Ciα,st-Ciα,att，从式(5)中消去非线性项，可以得到同相导数与异相导数之间的线性关系式为

Ciq=Ciq,att-τ(Ciα-Ciα,att)

(6)

式(5)还可以简化为

(7)

式中：

(8)

为待估计参数，而

(9)

为已知量。

从式(6)中能得到一个重要的结论，即以同相导数为自变量，异相导数为因变量，理论上在不同振荡频率下应呈线性关系，而斜率就是这个迎角对应的反映迟滞特性的时间常量，图2给出了某复杂构型飞机小振幅强迫振荡的动导数相图，从图中可见法向力系数和俯仰力矩系数对应的同相和异相导数呈现出明显的线性关系，特别是在大迎角下这种特征更加突出。

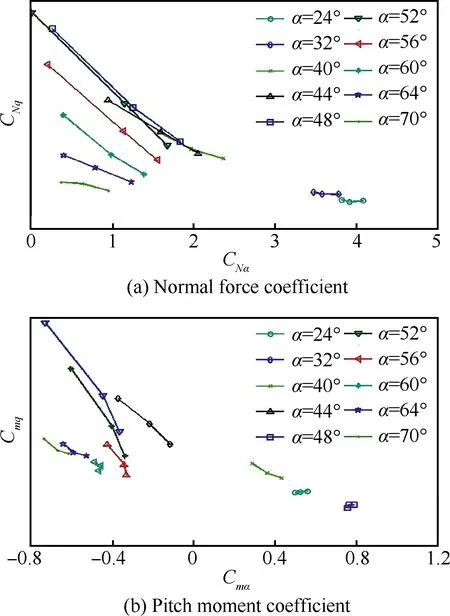
图2　不同中心迎角、不同频率下的同相及异相导数Fig.2　In-phase and out-phase derivatives at different angles of attack and frequencies

2.2线性模型参数辨识

上述线性微分方程模型，在每个不同中心迎角处，特征时间常数τ采用线性回归方法辨识，而其他参数采用牛顿-拉夫逊算法最小化如式(10)所示的判据函数即可获得未知参数b、c和d的估计结果。

(10)

式中：σ1为气动导数Ciα试验结果的相对误差；σ2为气动导数Ciq试验结果的相对误差。

图3给出了特征时间常数的辨识结果及参数估计的置信区间。图4给出了所有参数辨识完后解微分方程得到的线性模型预测结果和小振幅振荡气动力迟滞环的比较，在图4(a)中CN,test为法向力系数小振幅迟滞环试验数据，CN,model 1为法向力系数线性模型预测结果，CN,dyn为小振幅迟滞环中的非定常贡献量，ΔCN为涡破裂引起的法向力系数差量，而CN,st为静态试验数据，CN,model 2为法向力系数导数模型结果，图4(b)中的俯仰力矩元相关变量与法向力元类似。显然，线性微分方程模型明显改善了与大迎角小振幅试验气动迟滞环的拟合效果。

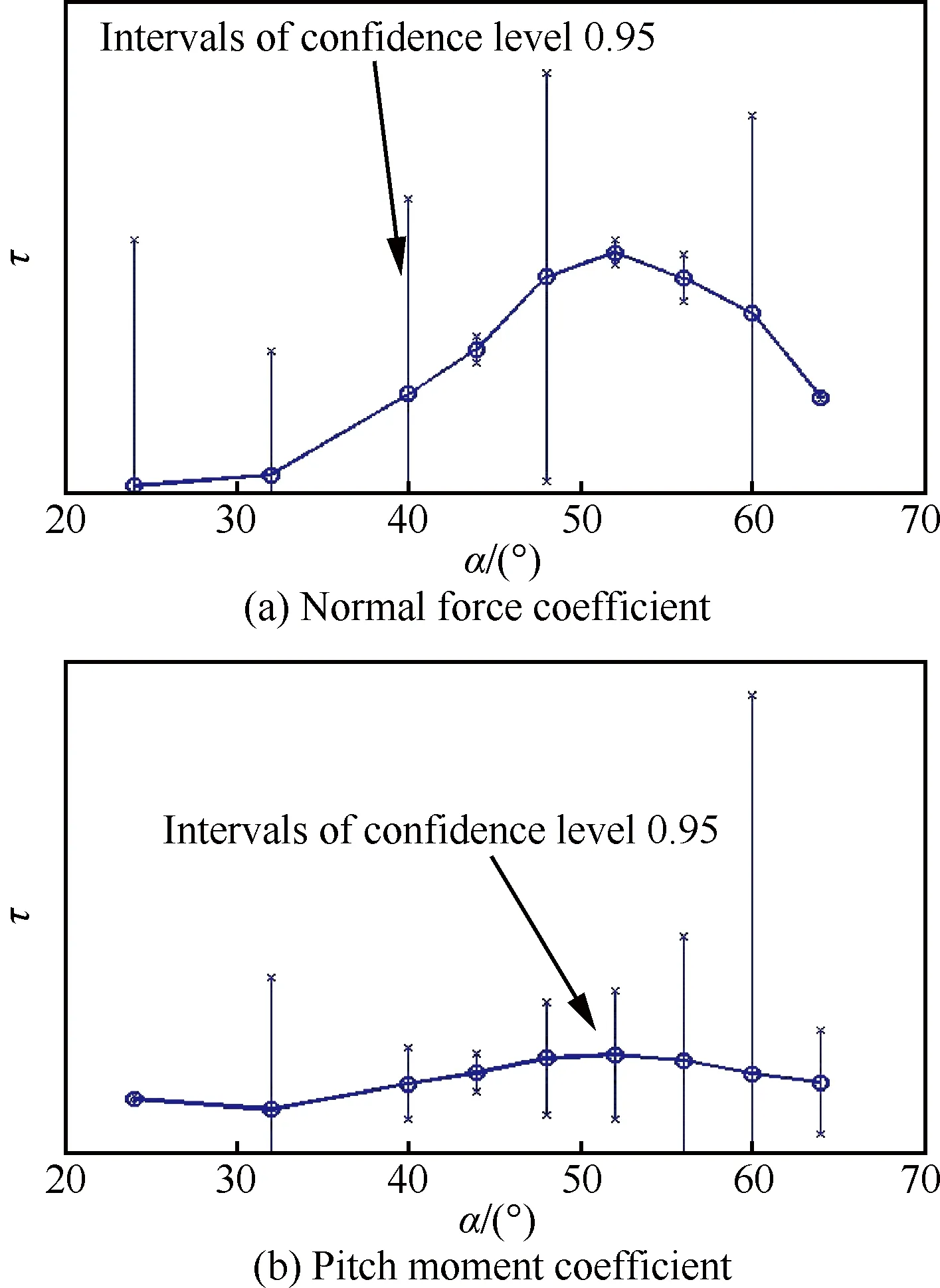
图3　特征时间常数随迎角的变化曲线Fig.3　Characteristic time scale varying with angle of attack

图4　线性模型与试验数据的比较Fig.4　Comparison between linear model and test data

3　非线性微分方程模型

3.1模型结构修正及辨识

随着振幅的增大，第2节中的线性数学模型可能失去其准度，为了使微分方程模型能反映大振幅的非定常气动力，就需要对式(2)做适当地修正，Goman的修正方程为

(11)

式中：n为多项式函数的阶次，取n=3；方程中k1(α)与特征时间常数相关，且当k2(α)=k3(α)=0时，k1(α)=1/τ(α)，从本质上讲，上述修正是因为有效特征时间常数τeff不仅与迎角有关，还与运动的时间历程相关，因而大振幅非定常气动力建模中需要辨识新的有效特征时间常数τeff。然而，不同于尖前缘大后掠三角翼[11]，在复杂构型布局的飞机模型气动力建模研究中发现，k2(α)和k3(α)参数对大振幅非定常气动力模型辨识精度影响并不大，针对实际情况，本文对模型进行如下形式的修正:

(12)

式中：Ci,st(α)为静态气动力系数；Ci,uns为非定常非线性气动力增量；τ1为反映流动拓扑结构迟滞效应的特征时间常数，且与迎角有关，如对于前机身带边条翼的战斗机布局在较小迎角处流场始终是脱体涡结构，并没有出现涡的破裂，因而特征时间常数通常较小，而在失速迎角附近，由于脱体涡的破裂与再附相对于运动本身会出现明显迟滞，因而此时的特征时间常数将会显著增大。

(13)

式中：τ1(α)、Aij为待辨识参数。实际上相关文献[20]研究表明，基于运动状态变量泛函的泰勒展开式的微分方程表达式是阶跃响应函数的一种简化形式，因而上述模型结构的修正有其理论依据。当模型的主体结构确定后，接下来要做的是确定式(13)中右边泰勒展开式的阶次，对不同阶次n计算模型的残差平方和SEE，SEE最小的模型即视为最优模型阶次。研究发现，随着n的增大，SEE逐渐变小，但当n达到一定数值时，SEE变化的速率显著减小，而此时如果继续增大阶次n反而会极大地增加模型辨识的复杂程度，综合考虑后本文取n=6。

3.2非线性微分方程模型参数估计

数学模型结构确定后，问题就成了根据辨识准则和试验数据求取模型中的待定参数，即参数估计问题，这是系统辨识定量研究的核心。而参数估计包括辨识准则和优化算法两部分。本文选用最大似然法准则作为辨识准则，选用牛顿-拉夫逊算法作为优化算法。实际上本文的气动力建模问题中只有一个观测量且不考虑过程噪声，因而最大似然准则和最小平方差和准则相同。

实践中发现，牛顿-拉夫逊法虽然具有不低于二阶的收敛速度，但对于非线性强的气动力模型容易发散，因为该算法要求目标函数的Hesse矩阵G(θ)在每个迭代点θk处是正定的，否则难以保证牛顿方向下降，为了克服这一缺陷，本文引进阻尼因子μk=0.5，使得矩阵Ak=G(θk)+μkI正定。

3.3算例分析

现在采用上述非线性微分方程模型和参数辨识算法来处理FL-8低速风洞中完成的某复杂构型飞机大幅谐波振荡试验数据，以检验上述修正模型结构及辨识算法的可行性。选取振幅为40°，频率分别为0.2、0.4、0.6和0.8Hz的试验数据及振幅为30°，频率分别为0.2、0.4和0.8Hz的试验数据作为训练样本，而选取振幅为30°，频率0.6Hz的振荡试验数据及振幅为20°，频率为0.2、0.4、0.6和0.8Hz的试验数据作为检验样本。特征时间常数随迎角变化，在0°～80° 迎角范围内将τ1(α)等间隔离散41个点，在0°～25° 迎角范围内，其初值取0.2～2.0，由前所述，在小迎角时翼面流场结构不变，流场内部涡系拓扑结构调整的滞后小，因而时间尺度小。而在25° 迎角后，涡破裂的出现将使涡系拓扑结构调整的滞后显著增大，其初值取线性模型中τ(α)的辨识结果，其他参数初值全取1。另外，由流动的物理特性可知该参数值不小于零，如果参数的辨识结果出现负值，即使收敛也将失去其本身的物理意义，实践发现，在30° 迎角后，特征时间常数通常是一个较大的正数，而在小迎角时可能出现负值，且参数出现负值时，虽然模型的精度较高，但其预测能力一般较差，为了避免此时该参数出现负值，在迭代的过程中人为地限制其值大于等于零，从而保证收敛后辨识结果不至于丧失其物理意义。图5给出了法向力系数参数辨识迭代收敛曲线。图中SEE表征残差平方和，而RR表征多层相关系数。

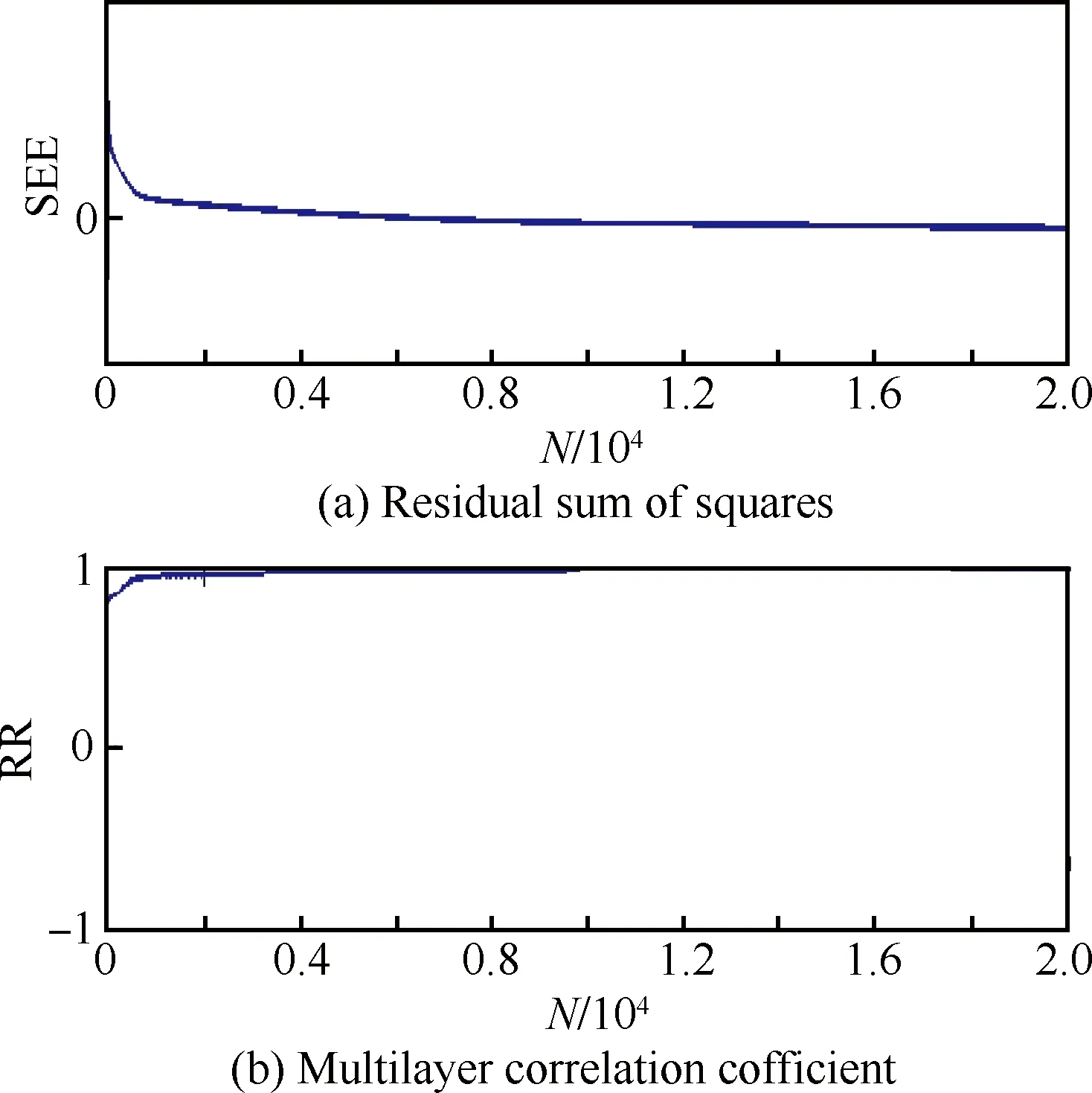
图5　迭代收敛曲线Fig.5　Iterative convergence curves

图6和图7给出了模型输出和训练样本的比较，其中Test表征大幅振荡试验数据，而Model表征非线性微分方程模型计算数据。从图中可以发现，经过修正后的非线性气动力模型与大幅振荡俯仰运动的试验数据吻合得很好。

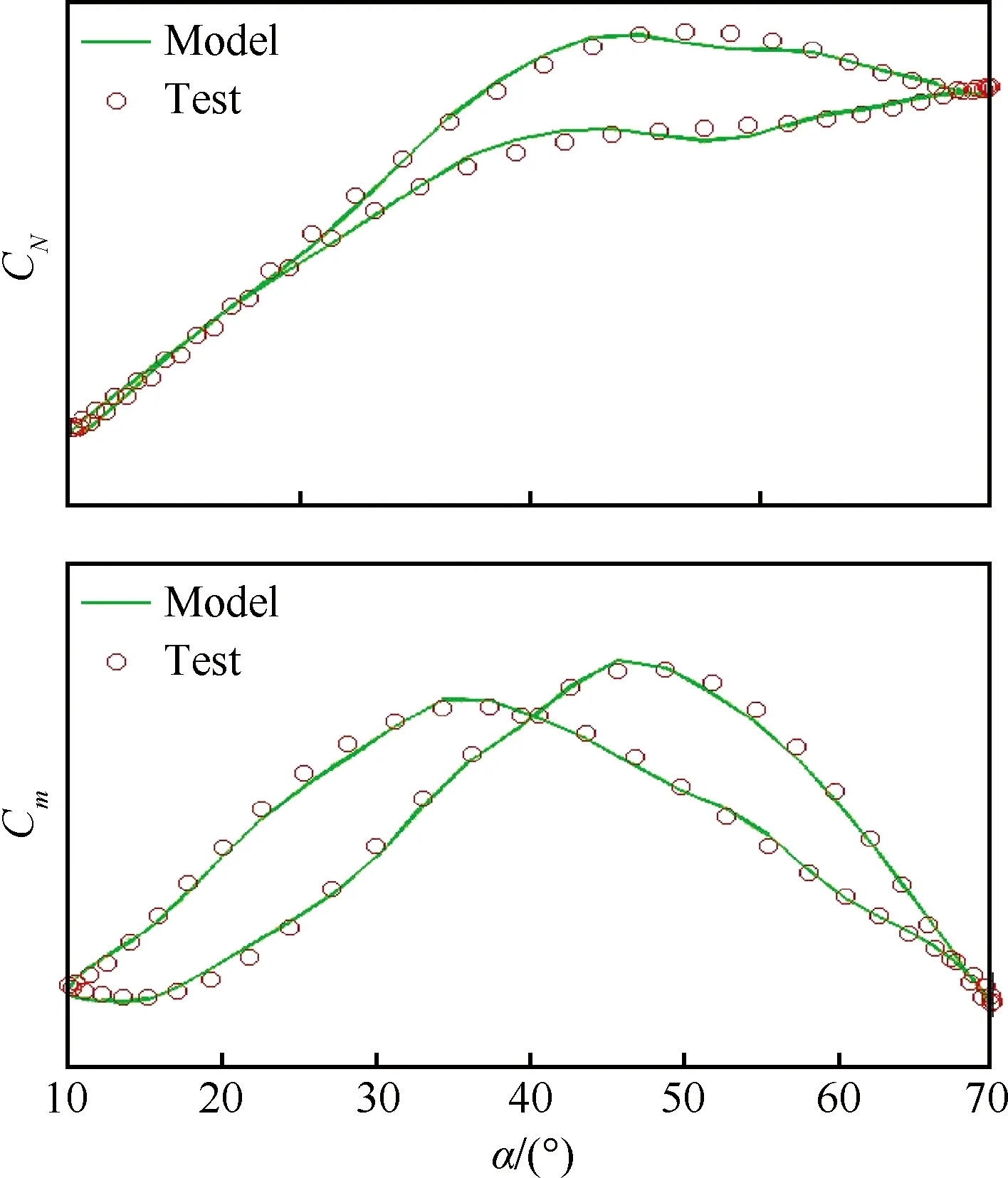
图6　非定常模型与试验数据的比较(f=0.2 Hz)Fig.6　Comparison between unsteady model and test data (f=0.2 Hz)

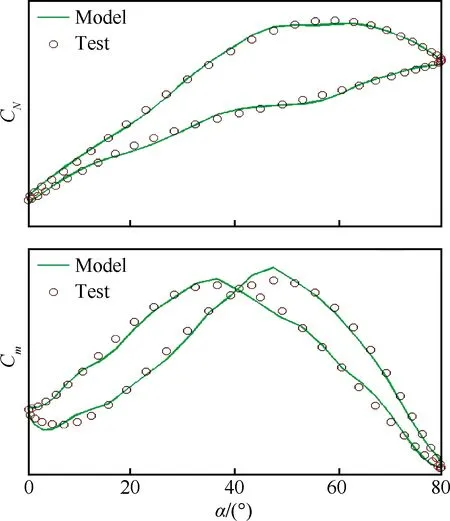
图7　非定常模型与试验数据的比较(f=0.6 Hz)Fig.7　Comparison between unsteady model and test data (f=0.6 Hz)

图8给出了模型预测和检验样本的比较，虽然模型的预测精度比建模精度略差，但依然能比较准确地预测。这就说明上述的模型结构辨识与参数估计足够准确。

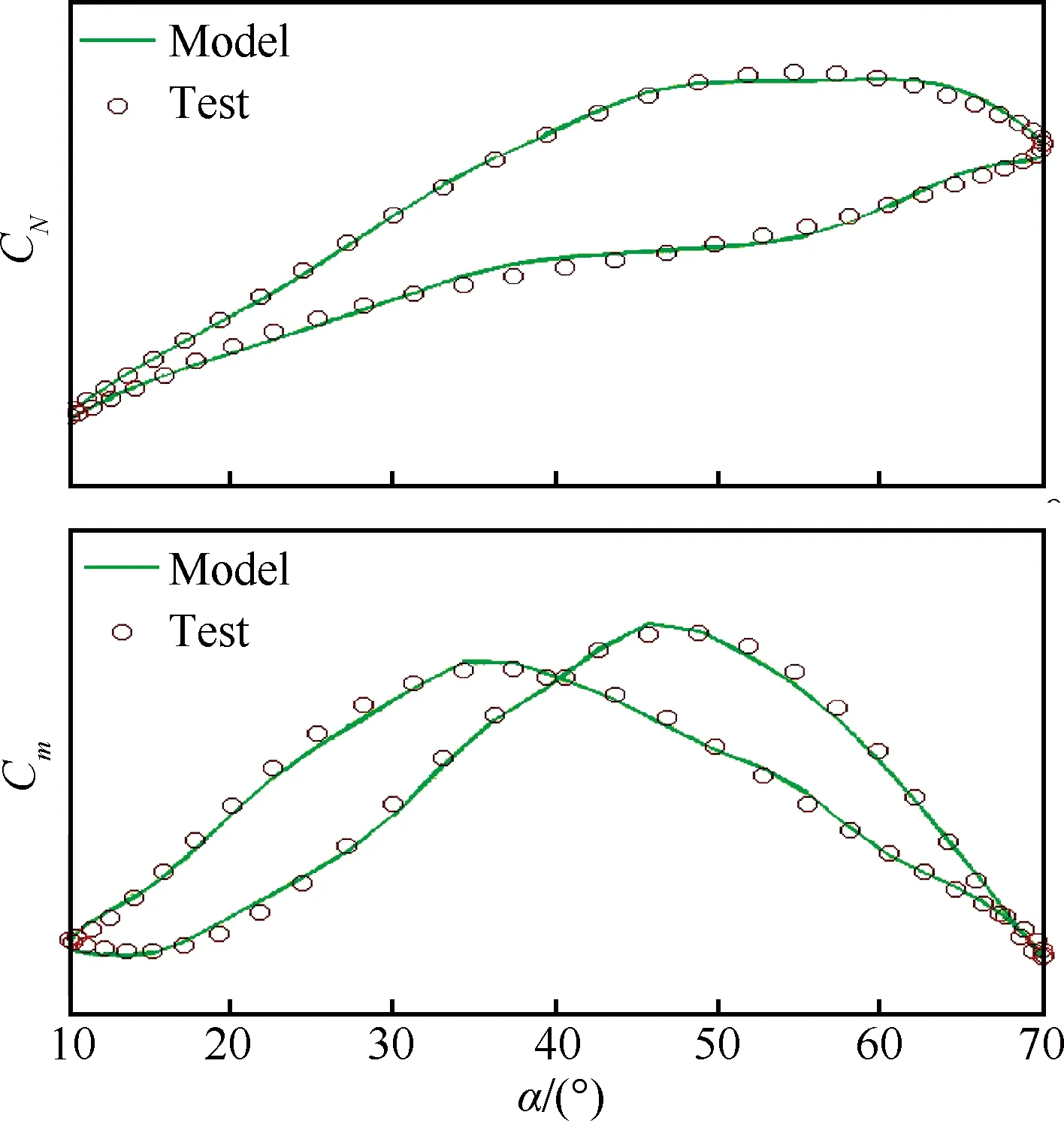
图8　非定常模型与试验数据30° 振幅值比较(f=0.6 Hz)Fig.8　Comparison between unsteady model and test data at 30° of amplitude (f=0.6 Hz)

3.4典型机动试验验证

为了进一步检验及评估上述非线性微分方程模型的有效性，这里将应用尾冲机动风洞模拟试验来验证。图9描述了尾冲机动的时间历程。图10 和图11给出了非线性微分方程模型预测和机动历程试验数据的比较，其中t表征机动历程的时间。可见预测结果和试验数据的一致性较好。

鉴于上述训练样本、检验样本及典型机动试验数据均与模型预测拟合较好，这就说明针对某复杂构型飞机布局的工程应用研究，本文建立的改进非线性微分方程模型能够较准确描述其大迎角非定常气动力特性。

图9　尾冲机动Fig.9　Tail slide maneuvers

图10　非定常模型与尾冲机动试验数据的比较(t=5 s)Fig.10　Comparison between unsteady model and test data in tail slide maneuvers (t=5 s)

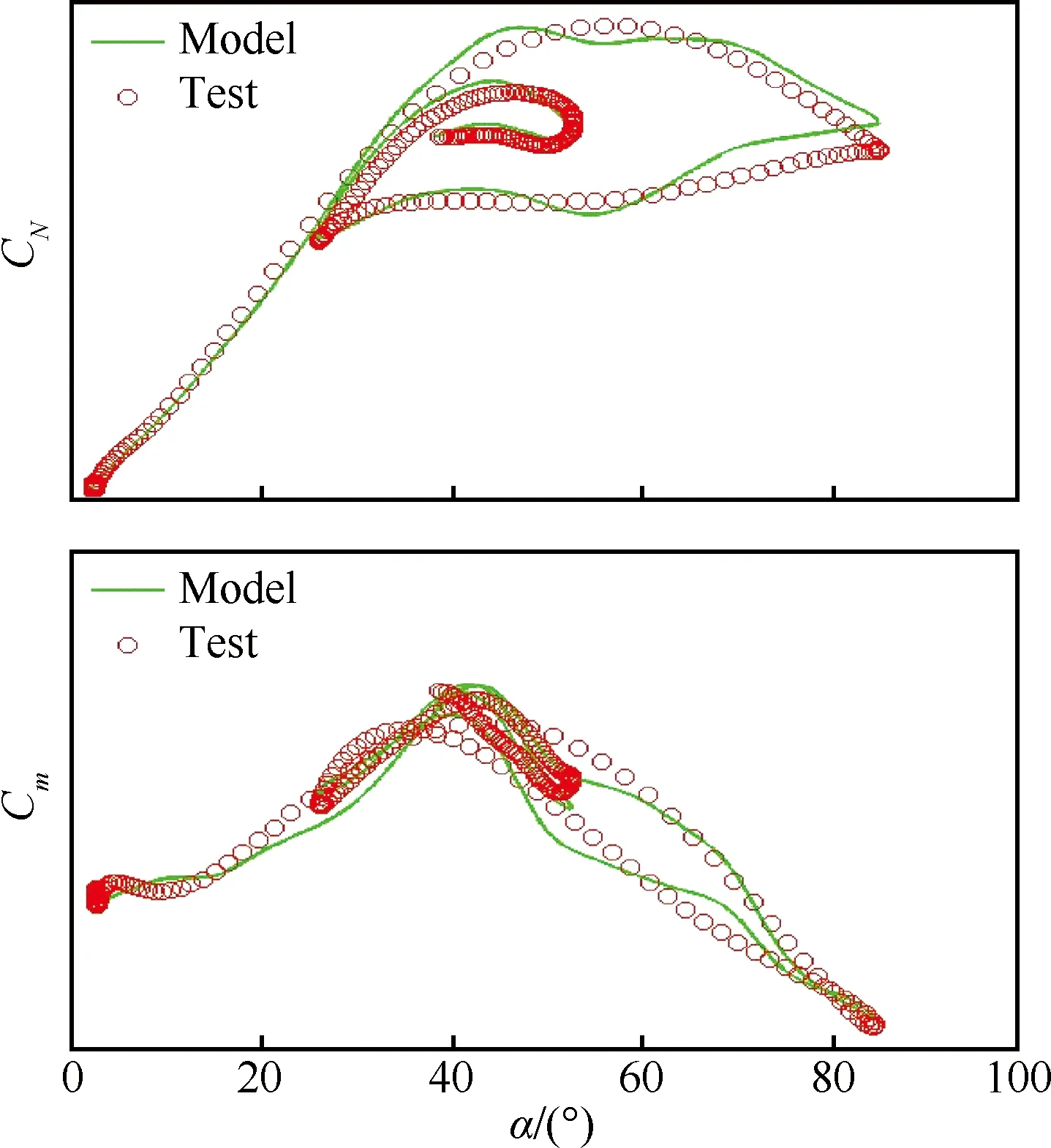
图11　非定常模型与尾冲机动试验数据比较(t=10 s)Fig.11　Comparison between unsteady model and test data in tail slide maneuvers (t=10 s)

4　结　论

1) 对于小振幅运动气动力迟滞环，微分方程模型的线性化表达式具有较高的预测准度，因而它为预测风洞试验难以实现的高频率动导数提供了一种途径。

2) 虽然相较于诸如粒子群等智能方法，牛顿类辨识算法程序设计相对复杂，但它无需设置参数范围且通过适当的修正通常具有良好的收敛性，且每步有明确的数学意义，适合面向工程的气动力建模研究。

3) 本文发展的非线性微分方程模型结构形式简单、物理意义清晰、工程针对性强，基本能够准确反映复杂构型飞机大迎角非定常气动力特性。

[1]JARRAH M A. Low speed wind tunnel investigation of flow about delta wings oscillating in pitch to very high angle of attack: AIAA-1989-0295[R]. Reston: AIAA, 1989.

[2]BRANDON J M, SHAH G H. Unsteady aerodynamic characteristics of fighter model undergoing large-amplitude pitching motions at high angles of attack: AIAA-1990-0309[R]. Reston: AIAA,1990.

[3]ROBERT C N. The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers[J]. Progress in Aerospace Sciences, 2003, 39(3): 185-248.

[4]ABZUG M J, LARRAB E. Airplane stability and control[M]. Cambridge: Cambridge University Press, 1977: 165.

[5]LIN G F, LAN C E, BRANDON J M. A generalized dynamic aerodynamic coefficient model for flight dynamics applications: AIAA-1997-3643[R]. Reston: AIAA, 1997.

[6]TOBAK M, SCHIFF L. On the formulation of the aerodynamic characteristics in aircraft dynamics: NASA TRR-456[R]. Washington, D.C.: NASA, 1976.

[7]GHOREYSHI M, JIRASEK A, POST M L. A computational investigation into the use of response functions for a aerodynamic loads modeling: AIAA-2010-3518[R]. Reston: AIAA, 2010.

[8]KLEIN V, MURPHY P C. Estimation of aircraft nonlinear unsteady parameters from wind tunnel data: NASA TM-1998-208[R]. Washington, D.C.: NASA, 1998.

[9]GOMAN M G, KHRABROV A N. State-space representation of aerodynamic characteristics of an aircraft at high angels of attack[J]. Journal of Aircraft, 1994, 31(5): 1109-1115.

[10]YI G F, FREDERICK H, LUTZE. Identification of unsteady aerodynamic modeling at high angle of attack: AIAA-1996-3407-CP[R]. Reston: AIAA, 1996.

[11]杨文, 尚祖铭, 卜忱. 一种基于升力面分解思想的横向状态空间模型[J]. 飞行力学, 2014, 32(5): 463-467.

YANG W, SHANG Z M, BU C. An lateral-directional state-space model based the idea of splitting the aircraft into several lifting surfaces or panels[J]. Flight Dynamics, 2014, 32(5): 463-467 (in Chinese).

[12]ABRAMOV M, GOMAN M G. Aircraft dynamics at high incidence flight with account of unsteady aerodynamic effects: AIAA-2004-5274[R]. Reston: AIAA,2004.

[13]ABRAMOV N B, GOMAN M G, KHRABROV A N, et al. Simple wings unsteady aerodynamics at high angles of attack: Experimental and modeling results: AIAA-1999-4013[R]. Reston: AIAA,1999.

[14]龚正, 沈宏良. 非定常气动力非线性微分方程建模方法[J]. 航空学报, 2010, 32(1): 83-90.

GONG Z, SHEN H L. Unsteady aerodynamic modeling method using nonlinear differential equations[J]. Acta Aeronautica et Astronautica Sinica, 2010, 32(1): 83-90 (in Chinese).

[15]WANG Z J, LAN C E. Fuzzy logic modeling of lateral-directional unsteady aerodynamics: AIAA-1999-4012[R]. Reston: AIAA, 1999.

[16]ZHONG J, WANG C, EDWARD L. Fuzzy logic modeling of nonlinear unsteady aerodynamics: AIAA-1998-4351[R]. Reston: AIAA,1998.

[17]WANG Q, HE K F. Unsteady aerodynamics modeling for flight dynamics application[J]. Acta Mechanica Sinica, 2012, 28(1): 14-23.

[18]史志伟, 明晓. 基于模糊聚类的模糊神经网络在非定常气动力建模中的应用[J]. 空气动力学学报, 2005, 23(1): 21-24.

SHI Z W, MING X. The application of FNN in unsteady aerodynamics modeling based on fuzzy clustering[J]. Acta Aerodynamic Sinica, 2005, 23(1): 21-24 (in Chinese).

[19]ALCORN C W. The X-31 aircraft advances in aircraft agility and performance[J]. Progress Aerospace Science, 1996, 15(32): 377-413.

[20]汪清, 蔡金狮.飞机大迎角非定常气动力建模与辨识[J]. 航空学报, 1996, 17(4): 391-398.

WANG Q, CAI J S. Unsteady aerodynamic modeling and identification of airplane at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 1996, 17(4): 391-398 (in Chinese).

杨文男， 硕士， 工程师。主要研究方向： 风洞动态试验技术及非定常气动力建模。

Tel: 0451-87570255

E-mail: yangwen19860804@163.com

卜忱男， 硕士， 研究员。主要研究方向： 风洞动态试验技术。

Tel: 0451-87571476

E-mail: buchen.1975@126.com

Unsteady aerodynamic modeling and identification fora complicated aircraft configurations

YANG Wen, BU Chen*, SUI Jianjun, SHANG Zuming

Department of Aerodynamics Development, AVIC Aerodynamics Research Institute, Harbin150001, China

Adequate modeling of nonlinear and unsteady aerodynamics at high angle of attack flight is important for the design of future fighters with high maneuverability and stealth as well as for the improved prediction of normal aircraft configuration’s dynamics. The limitations for conventional aerodynamic derivatives model based on longitudinal small amplitude experimental date and large amplitude experimental date at high angle of attack had been analyzed. The dynamic linear and nonlinear aerodynamic model approximating the vertical and separated flow time lag effects is considered along with the conventional aerodynamic model. Using the model the unsteady aerodynamics of one aircraft in typical maneuver simulation tests is predicted. It is suggested that the structural modification of nonlinear differential equation model proposed in this paper is valid in different maneuvers for complicated aircraft configurations, which bears proof on the practicality of the flight dynamics analysis.

large angle of attack; unsteady aerodynamic; time lag; differential equation; typical maneuver

2016-01-25； Revised： 2016-02-15； Accepted： 2016-03-14； Published online： 2016-04-0611：39

. Tel.： 0451-87571476E-mail: buchen.1975@126.com

2016-01-25； 退修日期： 2016-02-15； 录用日期： 2016-03-14；

时间： 2016-04-0611:39

www.cnki.net/kcms/detail/11.1929.V.20160406.1139.004.html

.Tel.： 0451-87571476E-mail: buchen.1975@126.com

10.7527/S1000-6893.2016.0094

V212.1

A

1000-6893(2016)08-2464-08

引用格式： 杨文，卜忱， 眭建军， 等． 面向复杂构型飞机的非定常气动力建模与辨识 [J]． 航空学报, 2016, 37(8): 2464-2471. YANG W, BU C, SUI J J, et al. Unsteady aerodynamic modeling and identification for a complicated aircraft configuration [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2464-2471.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160406.1139.004.html