考虑热力耦合的轨道车轮辐板参数优化研究

文永蓬，周伟浩，徐小峻，尚慧琳, 李琼

(1. 上海工程技术大学 城市轨道交通学院，上海 201620；2. 上海应用技术大学 机械工程学院，上海 200235)



考虑热力耦合的轨道车轮辐板参数优化研究

文永蓬1，周伟浩1，徐小峻1，尚慧琳2, 李琼1

(1. 上海工程技术大学 城市轨道交通学院，上海 201620；2. 上海应用技术大学 机械工程学院，上海 200235)

以提高双S型轨道车轮的综合性能为目的，建立双S型轨道车轮模型，采用轨道车轮的热力耦合计算方法，讨论双S型轨道车轮辐板在热力耦合条件下的几种优化思路，通过正交实验的方法对双S型轨道车轮辐板的关键参数进行优化。研究结果表明：当S弯方向为正以及结合圆弧处于正中位置时，双S型辐板车轮具有较好安全性能；双S型轨道车轮的辐板厚度以及靠近轮辋处的圆弧半径对双S型轨道车轮性能的影响较大。该研究不仅适用于双S型轨道车轮的结构特性分析，同时还对其他辐板轨道车轮的优化设计具有重要的参考价值。

热力耦合；轨道车轮；疲劳强度；正交实验；参数优化

在城市轨道车辆运行过程中，由于站间距短、行车密度高等因素造成车辆频繁的启动和制动，车轮和轨道的摩擦、车轮与闸瓦的摩擦产生大量的热，引起车轮产生较大的热载荷，与此同时，车轮还承受来自车辆的全部载荷，热载荷和结构载荷剧烈的共同作用往往造成车轮的疲劳损伤[1]。车轮的辐板是轮辋和轮毂的重要连接部件，在热力耦合载荷作用下起到承上启下的作用，对车轮的性能具有重要的影响。近年来，对车轮的疲劳分析及优化设计进行了大量报道[2-13]。早期对车轮疲劳问题的研究大多只考虑结构载荷的作用[2-4]，研究车轮在直道、弯道以及道岔处的应力大小，并算出安全系数与许用安全系数比较。目前，越来越多学者已经注意到温度的改变对于车轮疲劳的影响，重视列车在踏面制动时伴随着闸瓦与踏面间的摩擦车轮表面产生大量的热，认为温度的变化对车轮使用寿命的影响不可忽略。张萍[5]探讨了热流密度的加载方式，为车轮的热分析及热力耦合分析提供了重要的参考价值；Seo等[6-8]研究了车轮的热疲劳问题，对车轮热疲劳寿命预测方法进行了探讨；候耐等[9-11]通过对车轮在结构载荷、热载荷及2个载荷共同作用下的研究分析，认为结构载荷和热载荷的共同作用是导致车轮疲劳失效的主要原因。对于车轮的优化设计，徐传来等[12]通过APDL语言对轨道车轮进行参数化建模，运用ANSYS一阶优化工具对车轮截面进行形状化优化，其优化后车轮的质量少，但是应力有所增加；刘林芽等[13]通过遗传算法对单S型辐板车轮的辐板关键参数进行优化，以声辐射功率为优化目标，优化后的车轮声辐射功率较标准车轮声辐射功率在大部分频段上均有所减小。总之，以上研究很少考虑到热力耦合下轨道车轮辐板的参数优化设计，也未能针对轨道车轮辐板多参数的特点提出多目标的优化策略。为此，研究热载荷和结构载荷的共同作用对轨道车轮的影响，以抗热损性较好的双S型车轮[14]作为研究对象，分析双S型车轮辐板的结构特点，保持车轮的轮毂和轮辋不变，针对轨道车轮辐板提出多目标结构优化思路，得到几种优化后的轨道车轮辐板，并进一步分析比较优化后车轮的最大耦合应力、质量和踏面温度等特性。

1　轨道车轮有限元模型

1.1双S型车轮模型

上海4号线使用的是马钢生产的国产车轮ZD840，为双S型车轮。以该双S型车轮为研究对象，利用ANSYS有限元分析软件进行建模，在建模过程中忽略对计算结果较小的圆弧等细节，采用8节点的六面体单元SOLID70建立有限元模型，该双S型车轮的有限元模型中共含有21 490个节点和19 308个单元，划分好网格的模型如图1所示，该车轮材料为R9T，其基本属性如表1所示。

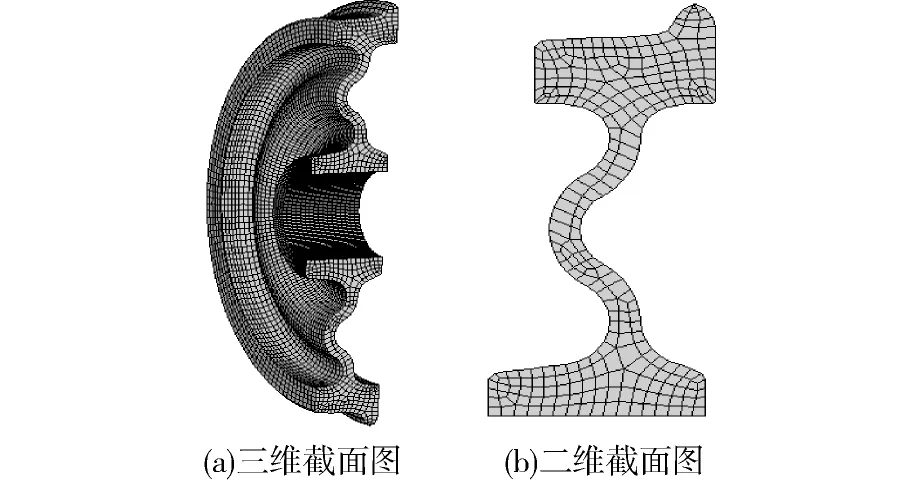
(a)三维截面图；(b)二维截面图图1　双S型车轮有限元模型Fig.1 FEM model for the double S rail wheel

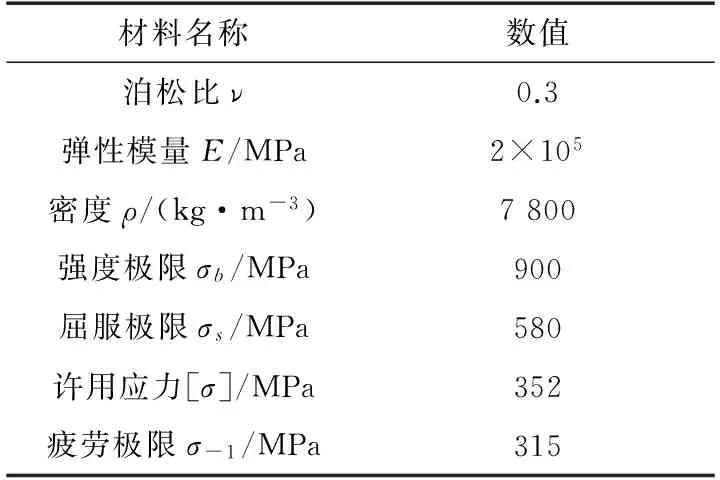
材料名称数值泊松比ν0.3弹性模量E/MPa2×105密度ρ/(kg·m-3)7800强度极限σb/MPa900屈服极限σs/MPa580许用应力[σ]/MPa352疲劳极限σ-1/MPa315

1.2载荷工况及加载条件

我国城市轨道车辆车轮尚未建立计算载荷和计算载工况标准，一般是基于国际铁路联盟UIC510-5或欧盟的BS EN13979-1标准进行。在轨道车辆运行过程中，车轮受到轮轨之间的三向应力，包括横向力、纵向力和垂向力，其中横向力和纵向力的方向有2个，垂向力的方向为竖直向上，但是列车弯道或过道岔运行时，由于转向架两侧重量分配不一致，使得一侧的轮轨间垂向力大于另一侧，导致两侧车轮受到的垂向力位置和大小均有区别。除了轮轨作用力，车轮还受到制动时闸瓦施加的闸瓦力，包括闸瓦压力和闸瓦摩擦力，其中，闸瓦摩擦力根据车轮运行方向不同有2个方向。基于已有的国外2个标准，考虑车轮结构载荷(计算见文献[15])和热载荷共同作用，基本涵盖了列车运行时的制动过程中车轮受到的各种载荷情况。

2　轨道车轮的热力耦合计算方法

2.1温度场分析

温度场分析首先要确定热载荷条件，包括环境温度、热流密度和换热系数。在计算热载荷时用到的轨道车轮相关参数及制动条件如表2所示，其热力学计算参数如表3所示。

表2　轨道车轮参数及制动条件Table 2 Parameters and braking conditions of the rail wheel

表3　轨道车轮热力学参数Table 3 Thermodynamic parameters of the rail wheel

2.1.1环境温度

根据城市轨道交通车辆车轮所处的工作条件，选取环境空气温度为24 ℃，车轮自身表面温度为40 ℃。

2.1.2热流密度

采用能量法进行计算，假设城市轨道交通车辆在制动过程中减少的动能全部转化为热能，根据动能定理以及热流密度q的计算公式可得：

(1)

式中：m为列车质量；v0为初速度；t为制动时间；S为踏面与闸瓦的接触面积；D为轨道车轮直径；n为闸瓦数；l为闸瓦宽度；η为热流分配系数。

2.1.3换热系数

对流换热系数可由经验公式[16]，求得对流换热系数h的计算公式：

h=16.7(1+1.33v)

(2)

式中：v为车辆运行速度。

由于温度场分析属瞬态热分析，所以在选择分析类型时选择瞬态分析，将以上计算得到热载荷值施加到双S型车轮模型上，对车轮制动过程中的温度场进行计算分析，由表2中制动减速度和制动初速度可计算出制动时间约为17 s。图2为温度最高时刻即10 s时的温度云图，图3为制动过程中车轮踏面温度随时间变化关系图，车轮在制动过程中踏面温度先增大后减小，在10 s时刻车轮踏面温度最大为192.2 ℃。

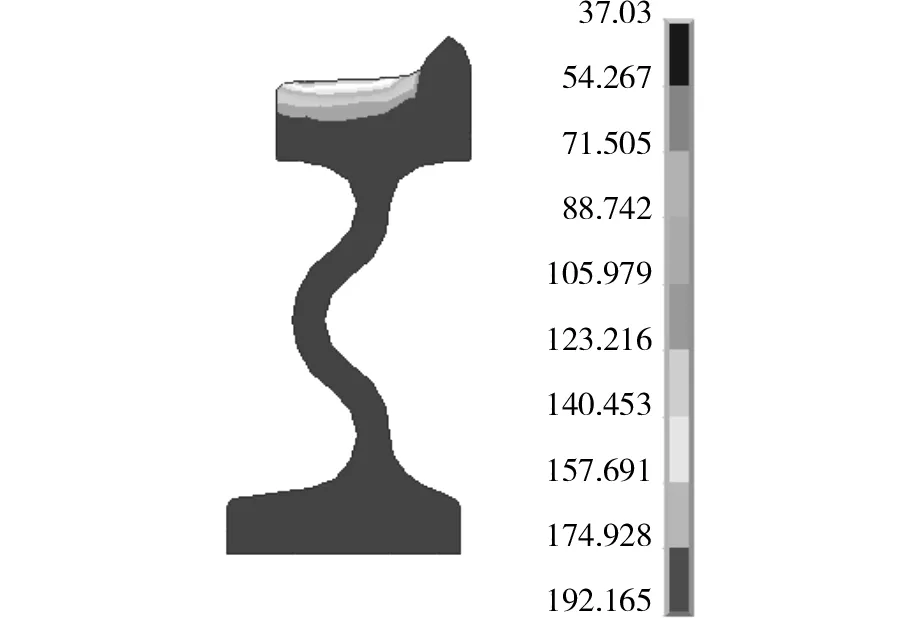
单位：℃图2　双S型车轮温度云图Fig.2 Temperature contour for the double S rail wheel

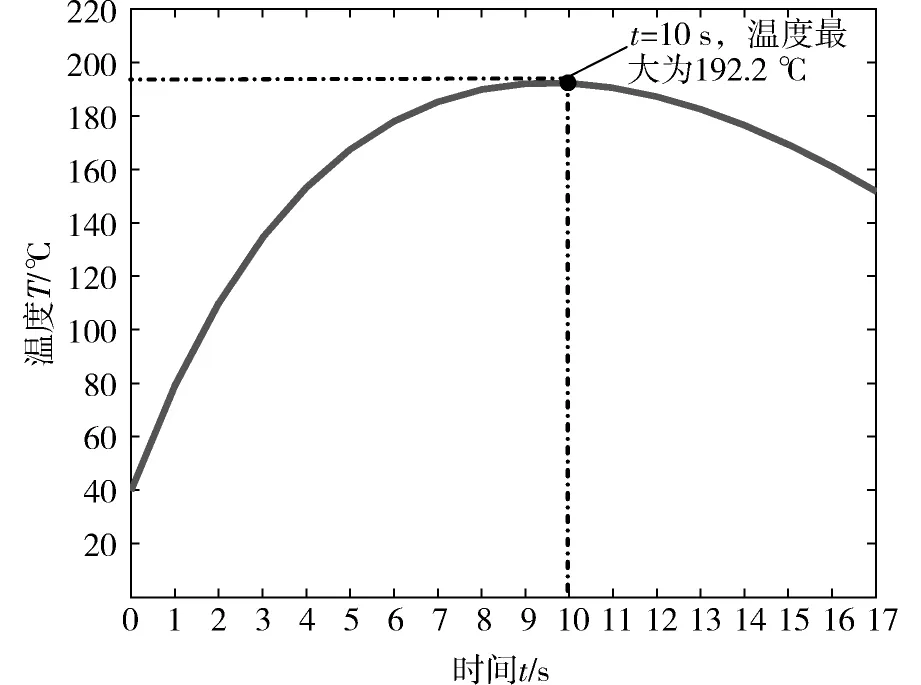
图3　双S型车轮17 s内踏面最高温度变化情况Fig.3 Maximum tread temperature for the double S rail wheel within 17 s

2.2热力耦合分析

采用间接耦合法，首先将热分析模型中的热单元SOLID70转换为结构单元SOLID185，再将轨道车轮热分析中得到的温度场各节点温度载荷作为体载荷施加到车轮上。并且，为了保持耦合前后的完整性，在热应力分析时建立与温度场一致的载荷步[17]。得到制动过程中车轮的热力耦合情况，图4为制动结束时刻热力耦合应力云图，由图4可知，制动结束时，车轮最大应力位于辐板处，最大应力约为120.4 MPa。图5为整个制动过程中最大耦合应力点耦合应力的变化情况，由图5可知，最大耦合应力随着制动时间逐步增大，在制动结束时刻达到最大值。

单位： Pa图4　双S型车轮耦合应力云图Fig.4 Thermal-mechanical coupling stress contour for the double S rail wheel

图5　双S型车轮17 s内辐板最大耦合应力变化情况Fig.5 Maximum thermal-mechanical coupling stress for the double S rail wheel within 17 s

综上，双S型车轮的踏面温度最大值出现在制动过程中，而热力耦合应力最大值出现在制动结束时刻。这2个性能参数描述了双S型车轮重要的特性，踏面温度与车轮踏面材料的属性相关，热力耦合应力与车轮的寿命相关。因此，在下面的研究中，把制动过程中踏面最高温度和制动结束时刻最大耦合应力，作为热力耦合下车轮的评价指标。此外，为节省成本，把车轮轻量化也作为一项评价指标。

3　不同辐板参数下双S型车轮性能

图6为双S型辐板车轮结构特征图。如图6所示，双S型车轮辐板存在2个S型弯和连接2个S弯的过渡圆弧三部分组成，S弯的厚度均为D。下面S弯形同“S”，称为正S弯；上面S弯形同反“S”，称为反S弯。保持双S型车轮的阴影部分(轮辋和轮毂)固定不动，即a点、b点、c点和d点固定不动，将辐板的空间作为辐板设计域。

在辐板设计域内，考虑双S型车轮辐板2个S弯的正反方向、结合圆弧的位置、S弯半径及辐板厚度，可分以下3种情况热力耦合分析。

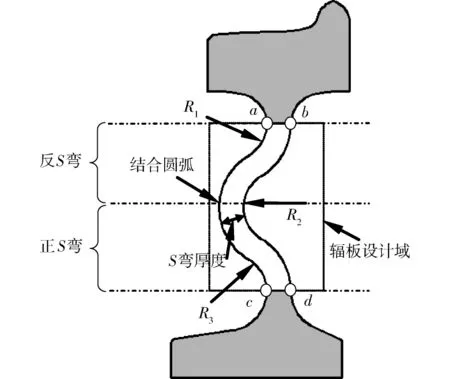
图6　双S辐板车轮结构特征图Fig.6 Structural features for the double S rail wheel

3.1S弯方向

在双S型车轮中，规定双S型车轮下面的S弯方向为双S车轮的方向，则原车轮为正双S车轮，可以建立反双S车轮，正双S车轮和反S车轮的二位截面如图7所示，并对反双S车轮进行热力耦合分析，其结果如表4所示。

图7　正、反双S车轮的二维模型Fig.7 Forward two dimensional model and the reverse one for the double S rail wheel

Table 4 Comprehensive performance comparison of the forward model and the reverse model for the double S rail wheel

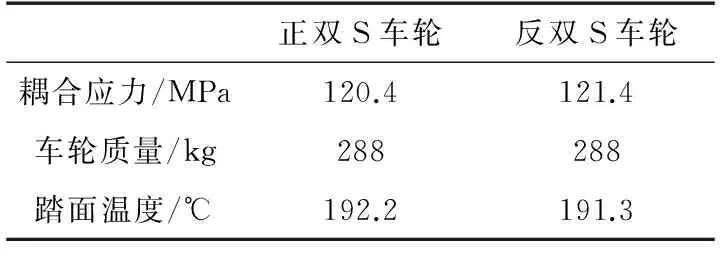
正双S车轮反双S车轮耦合应力/MPa120.4121.4车轮质量/kg288288踏面温度/℃192.2191.3

表4中，正双S车轮和反双S车轮的质量一样，踏面温度和耦合应力均差不多，由于主要考虑耦合应力，正双S车轮的耦合应力略小于反双S车轮，因此，正双S车轮性能优于反双S车轮，下面的分析中，均针对正双S车轮进行。

3.2结合圆弧位置

在正双S车轮辐板中，2个S弯呈轴对称分布，2个S弯的大小和形状都是相同的，所以2个S弯中间结合圆弧就在辐板的正中间位置，现考虑2个S弯的大小形状不同，在重新建立模型的过程中，尽量保持车轮的质量以及结合圆弧的半径不变，对原双S车轮辐板进行修改，得到2个新的双S车轮模型，并和原模型进行对比，3个模型的二维截面特征如图8所示。

图8　结合圆弧位置不同的双S型车轮的二维模型Fig.8 Two dimensional model of the double S rail wheel for the different arc position

Table 5 Comprehensive performance comparison of three kinds of arc models for the double S rail wheel

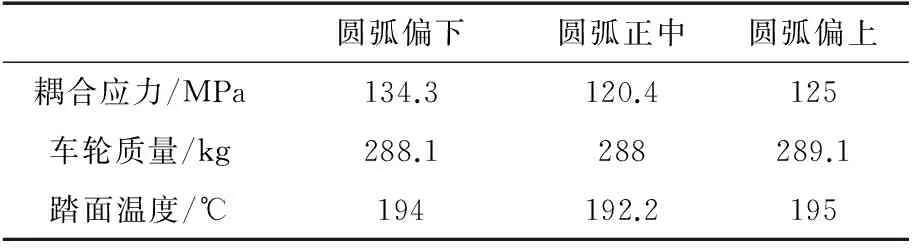
圆弧偏下圆弧正中圆弧偏上耦合应力/MPa134.3120.4125车轮质量/kg288.1288289.1踏面温度/℃194192.2195

对由于结合圆弧位置不同引起的新双S辐板车轮进行热力耦合分析，结果如表5所示。由表5可知，当结合圆弧在车轮辐板正中位置时，车轮质量最小，踏面温度最低，辐板耦合应力也最低，因此，结合圆弧在正中位置时，双S型车轮的性能较优。

3.3S弯半径及辐板厚度

由以上讨论可知，S弯方向和结合弧位置在一定范围内发生变化时，结合圆弧在辐板正中间的正双S型车轮是相对较优的。因此，本节主要对S弯方向及结合圆弧位置相对较优的原车轮辐板的4个尺寸参数进行讨论。

根据图6，双S型车轮辐板由3段等半径圆弧R1,R2和R3组成，且S弯的厚度D不变。现以R1,R2,R3和D这4个车轮辐板关键参数作为优化变量，以车轮辐板最大耦合应力、车轮质量和车轮踏面最高温度作为优化目标，现对每个变量参数赋予3个值，通过对这4个关键变量随机组合来寻找优化参数，共81种组合，由于实验次数较多，故本文采用可减少计算量的正交实验设计方法进行分析。

正交实验设计方法[18]是实验设计中的一种优化方法，利用数理统计的原理对实验结果进行科学地分析，通过少数实验就能够了解到各个因素对实验指标的影响情况，并且能够确定各个因素影响的主次顺序，从而找出优化参数组合。

采用正交实验的设计方法，分析辐板的4个参数对双S型车轮性能的影响，找出性能较优的参数组合，从而获得优化车轮。本实验中有4个因素A,B,C,和D，分别对应辐板参数R1,R2,R3和D。每个因素有3个水平，即每个因素对应的3个值，列出所有因素水平表，如表6所示。

利用正交实验的设计方法，选用“四因素三水平”正交表L9(34)，每个实验条件做3次，每次实验对3个指标测定，并取平均值，实验方案及其实验结果如表7所示，分析比较计算得到的实验数据，进而选取出较优的双S型车轮辐板的参数组合。

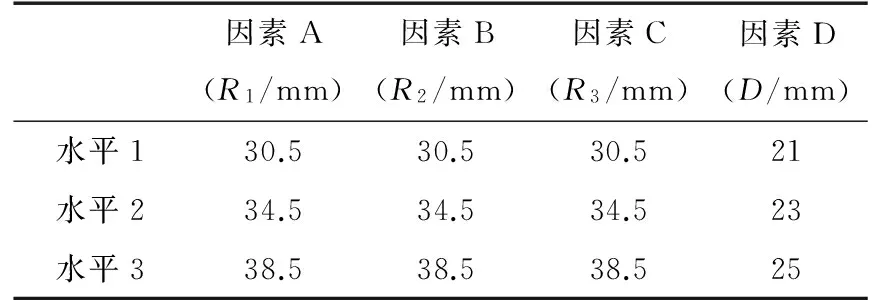
表6　因素水平表Table 6 Factors and levels table

表7　实验方案及结果Table 7 Experimental scheme and results

根据实验分析结果，可绘制出各个优化目标的效应曲线图，如图9所示。

由图9可以得出各优化目标下以及综合条件下双S型车轮辐板参数的优化组合，分析过程如下：

1)耦合应力为主

由图9(a)可知，在单纯以耦合应力为优化目标下，各因素的主次顺序为D>B>A>C，根据每个因素的每个水平的平均值大小可以得出耦合应力优化组合为A2B1C2D3(优化模型1)。

2)质量为主

由图9(b)可知，在单纯以质量为优化目标下，各因素的主次顺序为D>B>C>A，根据每个因素的每个水平的平均值大小可以得出耦合应力优化组合为A3B3C3D1(优化模型2)。

3)踏面温度为主

由图9(c)可知，在单纯以踏面温度为优化目标下，各因素的主次顺序为D>B>C>A，根据每个因素的每个水平的平均值大小可以得出耦合应力优化组合为A2B3C1D3(优化模型3)。

4)综合平衡考虑

在以上3个优化目标中，耦合应力关系到双S型车轮的行车安全及使用寿命，为主要优化目标，其次考虑成本等目标，兼顾车辆轻量化和车辆材料的加工工艺的要求。因此，优化目标主次顺序为：耦合应力>质量>踏面温度，根据优化目标的主次顺序，可确定因素D和因素B对车轮性能影响较大，因素C和因素A相对较小。

对于因素D：因素D对3个目标的影响均较大，但主要考虑的指标是耦合应力最小，故选D3，此时，踏面温度D3也是较优的。

对于因素B：因素B对3个目标的影响也较大，其影响程度仅次于D，从耦合应力角度选B1。

对于因素C：因素C对3个目标均是次要因素，耦合应力C1和C2差不多，从踏面温度角度选C1。

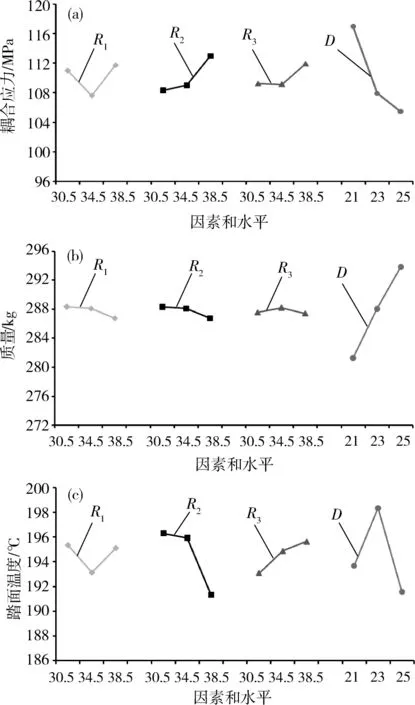
(a)耦合应力效应曲线;(b)质量效应曲线；(c)踏面温度效应曲线图9　各优化目标的效应曲线Fig.9 Effect curve of each optimization objective

对于因素A：因素A对以上3个指标也是次要因素，从耦合应力、踏面温度角度选A2。

故综合考虑耦合应力、车轮质量以及踏面温度后，确定综合平衡选取的优化组合为：A2B1C1D3(优化模型4)。

图10分别建立上述以单目标优化时优化的3个模型以及综合目标优化的1个模型。由图10可知，4个模型的S弯半径和辐板厚度在原有的双S型车轮辐板的基础上都有一定程度的改变，优化后的双S型车轮耦合应力、车轮质量和踏面温度均发生变化，结果如表8所示。由表8可知，以上4种优化模型的耦合应力均有所下降，优化模型1,3和4的耦合应力下降的最明显，其中优化模型1的耦合应力比原车轮下降最多，达16.7%，但是这3个优化模型的质量却都有上升，但是最大不超过2.5%；优化模型2耦合应力较原车轮相近，但其质量比原车轮下降了2.8%；优化模型3的踏面温度较优，但只比原车轮低了0.9%。因此，由上述优化效果可知，不改变车轮辐板的基本形状，仅仅使S弯半径和辐板厚度微小的改变，若造成车轮质量增加，则可降低其耦合应力；对于踏面温度，仅改变辐板参数，其优化效果不明显，但可通过使用优化材料属性来进行提升。

综上，以耦合应力、车轮质量以及踏面温度为优化目标，通过改变双S型车轮辐板2个S弯的正反方向、结合圆弧的位置、S弯半径及辐板厚度，确立了优化目标及设计参数的优先级，双S型车轮辐板厚度D和靠近轮辋处的圆弧半径R2这2个参数对车轮性能最灵敏，对双S型车轮综合性能影响显著。因此，今后在加工制造过程中这2个参数的加工误差需要格外关注。

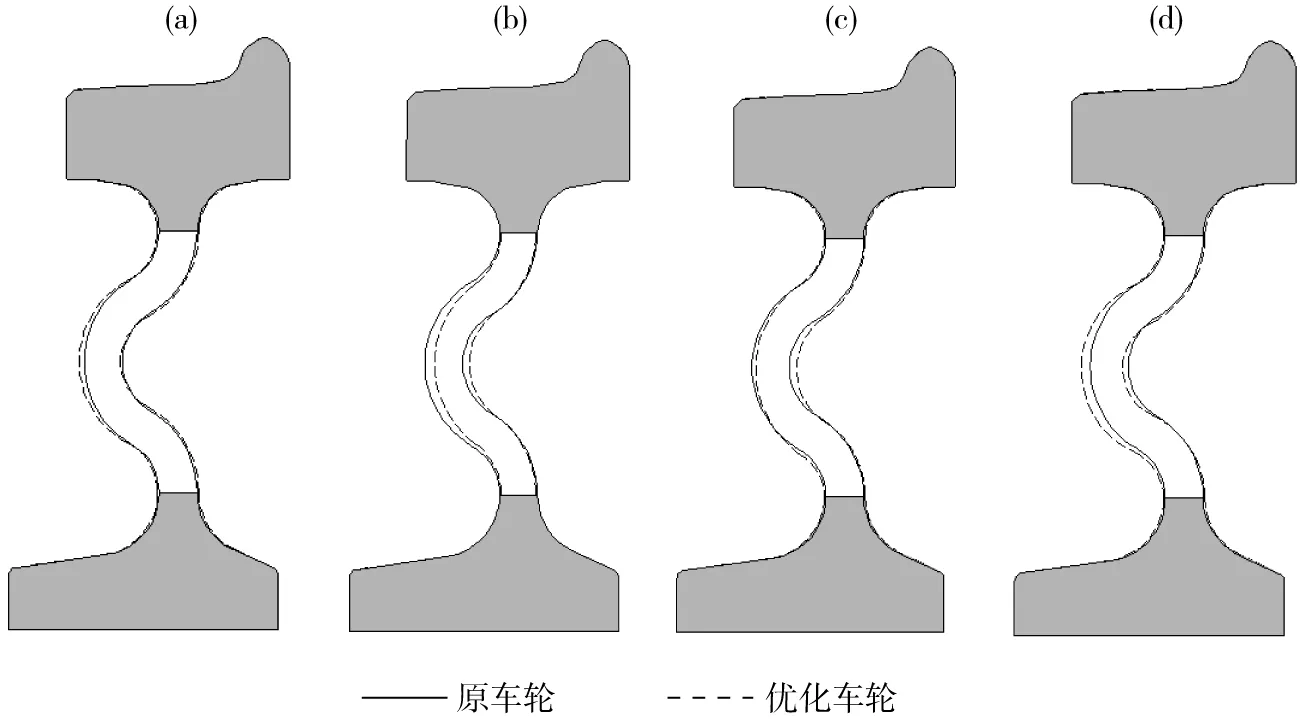
(a)优化模型1；(b)优化模型2;(c)优化模型3；(d)优化模型4图10　优化前后辐板形状比较图Fig.10 Comparison of results before and after optimization

优化车轮A2B1C2D3(模型1)A3B3C3D1(模型2)A2B3C1D3(模型3)A2B1C1D3(模型4)原车轮A2B2C2D2设R1/mm34.538.534.534.534.5计R2/mm30.538.538.530.534.5参R3/mm34.538.530.530.534.5数D/mm2521252523耦合应力/MPa100.3119.1104.7105.4120.4车轮质量/kg295.3279.9293292.9288踏面温度/℃192.3196190.4192.9192.2优化效果耦合应力降低16.7%质量降低2.8%温度降低0.9%耦合应力降低12.5%

4　结论

1)当 S弯方向为正以及结合圆弧处于正中位置时，双S型辐板车轮具有较好安全性能，且双S型车轮辐板厚度D和靠近轮辋处的圆弧半径R2对双S型车轮性能影响较显著，在加工制造时，对车轮这两个参数需要格外重视。

2)根据双S型车轮多参数的特点，确立了以耦合应力为主、车轮质量和踏面温度为辅的优化思路，按照这个思路对辐板的4个尺寸参数进行平衡选优，从而得出综合性能较优的车轮，对多目标优化问题提供参考价值。

3)采用正交试验的方法对双S型轨道车轮进行参数优化，减少了实验次数，能快速直观地获得双S型车轮辐板的优化参数组合，为轨道车轮的优化设计提供了一条有效思路。

4)优化后的车轮较原车轮均有明显的优化效果，优化模型一的耦合应力比原车轮下降达16.7%，因此，考虑热力耦合效应，建议采用优化模型一为城市轨道双S型车轮的进一步研究的车轮模型。

[1] 文永蓬,尚慧琳,董其炜,等.城市轨道车辆车轮轮缘磨耗分析[J].科技导报,2013,31(26):40-43.

WEN Yongpeng, SHANG Huilin, DONG Qiwei, et al. Analysis on the wear of wheel flange for urban rail vehicle[J].Science & Technology Review,2013, 31(26):40-43.

[2] 何莹,刘志明,胡宝义.动车组车轮强度标准与分析方法[J].北京交通大学学报,2009,33(1) :15-19.

HE Ying,LIU Zhiming,HU Baoyi. EMU’s wheel strength standards and analytical methods [J].Journal of Beijing Jiaotong University,2009,33(1) :15-19.

[3] 丁辉.铁道车辆车轮强度分析和评定方法[J].铁道机车车辆,2003,23(4):12-14.

DING Hui.Intensity analysis evaluation method of the wheel of the railway vehicle[J].Railway Locomotive & Car,2003,23(4):12-14.

[4] 王宏林,李芾,黄运华.25 t轴重重载货车车轮强度分析[J].铁道车辆,2007,45(12):1-4.

WANG Honglin,LI Hu,HUANG Yunhua.Strength analysis of wheels for heavy haul freight cars with the axle-load of 25 t[J].Rolling Stock,2007,45(12):1-4.

[5] 张萍.地铁车轮踏面制动热负荷研究[D].成都:西南交通大学,2010.

ZHANG Ping.A study of thermal load of tred braking for metro wheel[D].Chengdu: Southwest Jiaotong University,2010.

[6] Seo J W,Kwon S J,Jun H K,et al.Effects of esidual stress and shape of web plate on the fatigue life of railway wheels[J].Engineering Failure Analysis,2009,16:2493-2507.

[7] Teimourimanesh S,Vernersson T,Lunden R,et al.Tread braking of railway wheels-temperatures generated by a metro train[J].Original Article,2014,228(2):210-221.

[8] 卢立丽.货车制动踏面热损伤研究[D].成都:西南交通大学,2007.

LU Lili.Research on tread brake heat injury of freight wheel[D].Chengdu: Southwest Jiaotong University,2007.

[9] 候耐.重载货车车轮踏面制动热负荷研究[D].成都:西南交通大学,2011.

HOU Nai.Heat load analysis of heavy-haul frecight car wheel for tread breaking[D].Chengdu: Southwest Jiaotong University,2011.

[10] 肖楠,谢基龙,周素霞.地铁车轮踏面制动疲劳强度评价方法及应用[J].工程力学,2010,27(9) :234-239.

XIAO Nan,XIE Jilong,ZHOU Suxia.Method to assess fatigue strength of tread breaking of mehicle wheel and its application[J].Engineering Mechanics,2010, 27(9):234-239.

[11] 徐传来,米彩盈,李芾.基于轴对称模型的货车车轮结构疲劳强度分析[J].交通运输工程学报,2008,8(6):20-23.

XU Chuanlai,MI Caiying,LI Fu.Structural fatigue strength analysis of wheel for freight car base on axisymmetric model[J].Journal of Traffic and Transportation Engineering,2008,8(6):20-23.

[12] 徐传来,米彩盈,周仲荣.基于APDL语言的车轮参数化形状优化[J].铁道学报,2011,33(11):23-27.

XU Chuanlai,MI Caiying,ZHOU Zhongrong.Wheel shape & parameter optimization based on APDL language[J].Journal of the China Railway Society,2011,33(11):23-27.

[13] 刘林芽,张斌,邵文杰,等.S型辐板车轮声辐射优化设计[J].交通运输工程学报,2013,13(5):55-60.

LIU Linya,ZHANG Bin,SHAO Wenjie,et al.Optimization design of acoustic radiation for S-form web plate wheel[J].Journal of Traffic and Transportation Engineering, 2013,13(5):55-60.

[14] 王庆峰.关于统一城轨车辆车轮型式的研究[J].现代城市轨道交通,2009(2):55-57.

WANG Qingfeng.Study on unification of wheel type of urban rail vehicles [J].Modern Urban Transit,2009(2):55-57.

[15] 田剑锋,赵永翔. Ф840mm地铁车轮疲劳强度分析[J].机械设计与研究，2013,40(10):45-49.

TIAN Jianfeng,ZHAO Yongxiang.Strength analysis of Ф840mm subway wheel[J].Journal of Machine Design and Research,2013,40(10):45-49.

[16] 陈倩,李芾,王军平,等.40t轴重货车制动热负荷分析[J].铁道机车车辆,2012,32(4):32-36.

CHEN Qian,LI Fu,WANG Junping,et al.ThermaI load anaIysis of wheels for 40t axle-load freight car under braking conditions[J].Railway Locomotive & Car,2012, 32(4):32-36.

[17] 李金良,肖楠,谢基龙.重载货车车轮踏面制动辐板热应力分析[J].机械工程学报,2012,48(12):133-138.

LI Jinliang,XIAO Nan,XIE Jilong.Thermal stress analysis of the heavy-haul freight car’s wheel web plate under the wheel tread braking[J].Journal of Mechanical Engineering,2012,48(12):133-138.

[18] 刘文卿.实验设计[M].北京:清华大学出版社,2005.

LIU Wenqing.Experiment design[M].Beijing: Tsinghua University Press, 2005.

Study on parameter optimization for the rail wheel considering thermal-mechanical coupling

WEN Yongpeng1,ZHOU Weihao1,XU Xiaojun1,SHANG Huilin2,LI Qiong1

(1. College of Urban Railway Transportation, Shanghai University of Engineering Science, Shanghai 201620, China;2. School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 200235, China)

In order to improve the comprehensive performance of the double S urban rail wheel, a double S rail wheel model was established. The method of thermal-mechanical coupling was introduced in this model. Considering the thermal-mechanical coupling, several thoughts of double S rail wheel optimization model were analyzed. The key parameters of double S rail wheel plate were optimized by the method of orthogonal experiment. The results show that the double S rail wheel has a good safety performance when S bending in the positive direction and circular arc in the center position. The plate thickness and the radius of circular arc near the rim have a greater influence on the performance of the double S rail wheel. The work is not only suitable for the structure analysis of double S rail wheel, but also has important reference value for the other rail wheel optimization design.

thermal-mechanical coupling; rail wheel; fatigue strength; orthogonal experiment; parameter optimization

2016-05-20

国家自然科学基金资助项目(11472176)；上海市自然科学基金资助项目(15ZR1419200)；上海市研究生教育创新计划学位点引导布局与建设培育项目(13sc002)

文永蓬(1979-)，男，江西永新人，博士，副教授，从事轨道车辆关键结构优化设计，轨道车辆振动与控制无轨道车辆故障诊断技术的研究；E-mail：yp_wen@163.com

U270.2

A

1672-7029(2016)10-2042-09