水泥-水玻璃双液注浆力学特性的试验研究

王小龙，王起才,2，张戎令,2，张亚昆，巫茂寅

(1.兰州交通大学 土木工程学院, 甘肃 兰州 730070；(2.道桥工程灾害防治技术国家地方联合工程实验室，甘肃 兰州 730070；(3.中铁二十一局集团路桥工程有限公司，陕西 西安 710000)



水泥-水玻璃双液注浆力学特性的试验研究

王小龙1，王起才1,2，张戎令1,2，张亚昆3，巫茂寅1

(1.兰州交通大学 土木工程学院, 甘肃 兰州 730070；(2.道桥工程灾害防治技术国家地方联合工程实验室，甘肃 兰州 730070；(3.中铁二十一局集团路桥工程有限公司，陕西 西安 710000)

通过测定水泥-水玻璃双液注浆压强0.4 MPa，距离注浆中心0.5 m，注浆龄期1，2，4和12 h高精度测斜管的变形，结合有限元软件ABAQUS，研究不同注浆龄期、不同深度水泥-水玻璃双液注浆的力学特性。试验结果表明：注浆龄期1，2，4和12 h，水泥-水玻璃双液注浆产生的注浆压力先增大后减小，再持续增大，最小值发生在注浆龄期2 h；各个注浆龄期测斜管变形内力Mises的最大值出现在注浆土层中心深度，测斜管的第二大变形内力出现在注浆土层与未注浆土层分界处。

水泥-水玻璃双液注浆；测斜管；注浆龄期；力学特性

随着城市发展和地下空间的开发，越来越多地遇到复杂地基及地下工程建设等问题。地基加固是否恰当关系到整个工程的质量、投资和进度[1]，地下空间开发势必进行基坑开挖，围护结构施工等行为，引起坑底隆起、支护后土体侧移以及坑外地面沉降等[2]，对既有建筑安全产生影响。因此，合理选择地基加固方法是保证建设工程顺利进行的重要途径之一。水泥-水玻璃浆液亦称CS浆液，两者混合后生成水泥胶，水泥胶凝固后的结石率可达98%～100%，结石的抗压强度较高，可提高土体抗压强度，改善土体的松散性和软弱性[3]。目前，双液注浆加固是隧道渗漏处理，既有建筑周围土体加固，地下工程泥水平衡调整的有效方法[4-8]。国内外许多学者对水泥-水玻璃双液注浆进行了研究[9-12]。然而，大多研究着眼于双液注浆胶凝时间、注浆工艺及改进方面，忽略了水泥-水玻璃双液注浆力学特性的研究。少量研究虽然考虑了水泥-水玻璃浆液的力学行为，但只着眼于最终效用，没有考虑不同注浆龄期、不同注浆深度水泥-水玻璃双液注浆力学行为的变化规律。本文通过测定注浆龄期1，2，4和12 h测斜管的变形，研究了不同注浆龄期水泥-水玻璃双液注浆产生的注浆力的变化规律并结合有限元软件ABAQUS分析不同注浆深度加固结构的内力分布规律。

1　试验

1.1试验方法

水泥-水玻璃浆液注入土体时，土体受到水泥-水玻璃浆液的挤压产生扰动，离注浆中心越近，水泥-水玻璃浆液越容易到达，土体受到挤压力越大，相应的该处测斜管变形越大。试验通过测定不同注浆参数下测斜管的变形，研究水泥-水玻璃双液注浆的力学特性。试验注浆压强为0.4 MPa，测斜管与注浆管间距为0.5 m，水泥-水玻璃双液注浆试验断面图如图1所示。

图1　水泥-水玻璃双液注浆试验断面图Fig.1 Cross-section diagram of cement-silicate double solution grouting test

1.2试验材料及仪器

1.2.1试验材料

试验用水采用自来水，水泥采用的是河南省卫辉市春江水泥有限公司生产的P.O42.5级普通硅酸盐水泥，水泥浆水灰比W/C=1∶1。按照国标(GB/17671—1999)检测，水泥各项指标如表1所示。水玻璃采用市场上销售的符合国家要求的水玻璃，水玻璃模数M=2.96，水玻璃溶液浓度Be’=35。水泥浆∶水玻璃=1∶1(体积比)。测斜管使用的是高精度铝合金测斜管，各项指标如表2所示。

1.2.2试验仪器

试验仪器有：1)GZJB型液压双液注浆泵，最大输送压强为7 MPa,最大水平输送距离为200 m，最大垂直输送距离为60 m，理论输出4 m3/h，工作原理如图2所示；2)测斜仪。

表1　硅酸盐水泥性能参数Table 1Portland cement performance index

表2　高精度铝合金测斜管参数Table 2 Parameters of high- precision aluminum inclinometer pipe

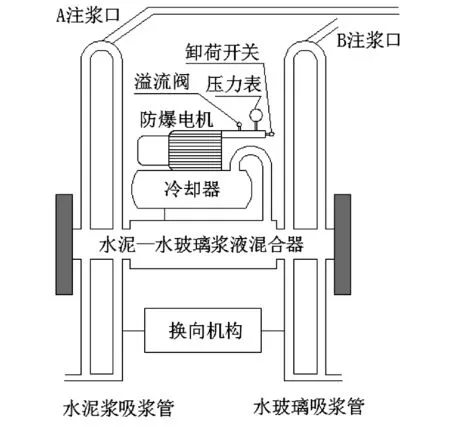
图2　水泥-水玻璃双液注浆泵工作原理Fig.2 Working principle of cement-silicate double solution grouting pump

1.3试验过程及数据处理

1.3.1试验过程

试验在粉质黏土区进行，试验区环境条件单一，没有外界因素对测斜管变形产生影响。利用注浆管将水泥-水玻璃混合料注入土层中，注浆土层4 m，上覆土层深度10 m。根据《建筑地基处理技术规范》(JGJ79—2012)，注浆管采用Φ42 mm，壁厚3 mm的金属管，为了使CS浆液准确注入加固土层，注浆管底部每隔10 cm横向开设2个Φ6 mm的小圆孔，小圆孔呈梅花型布置，注浆时浆液从小圆孔流入加固土层，注浆管其他部位均没有预留孔隙，如图1所示。

1.3.2数据处理

水泥-水玻璃双液注浆产生的测斜管变形由下式计算：

Δ=St-S0

(1)

式中：Δ为水泥-水玻璃双液注浆引起的测斜管变形，正值向注浆中心外侧偏移，负值向注浆中心内侧偏移；St为注浆龄期测斜管变形值；S0为测斜管的初始变形值。

2　结果与讨论

2.1水泥-水玻璃双液注浆不同龄期力学特性

距离注浆中心0.5 m，注浆压强0.4 MPa，不同注浆龄期测斜管变形如表3所示。从表3可以看出，注浆龄期1 h时，注浆段测斜管向注浆中心外侧倾斜，总体呈现出中间大两端小的态势，最大值在注浆加固土层中心深度处，为3.1 mm，最小值在注浆加固土层底部，为2.0 mm；注浆龄期2 h时，测斜管变形较1 h龄期减小，测斜管向注浆中心内侧偏移，出现最大、最小值的位置与1 h龄期相同，分别为1.5 mm和1.0 mm；注浆龄期4 h时，测斜管变形恢复，超过1 h龄期值，出现最大最小值的位置与1和2 h龄期相同，分别为3.5和2.2 mm；龄期12 h时，测斜管变形在4 h龄期的基础上持续增大，出现最大最小值的位置与龄期1，2和4 h均相同，为5.6和4.4 mm。这是因为，注浆龄期1 h时，水泥-水玻璃浆液在注浆压力作用下挤入土体，使土体变密实，测斜管在土体和CS浆液共同作用下向外倾斜。由于水泥-水玻璃浆液挤入土体破坏了原状土的固结特性，加上水泥-水玻璃浆液没有达到足够强度，注浆龄期2 h时，测斜管变形回弹。注浆龄期4 h时，水泥-水玻璃浆液胶凝性增强、强度增大，土体与水泥-水玻璃浆液重新组合成密实性更好的体系，而且水泥自身水化放热膨胀，在上述综合因素作用下，测斜管向注浆管外侧倾斜，变形较大。这一阶段，粉质黏土中的碱金属组分与水玻璃反应生成碱金属水合硅酸盐和二氧化硅凝胶，充填了粉质黏土中的孔隙，增加了粒间胶结力，使土体硬化，强度增加。注浆龄期12 h时，测斜管的变形在龄期4 h的基础上进一步增大，达到观测龄期峰值，加固土体的强度和密实度进一步增强。

表3各个龄期测斜管深层水平位移测试值

Table 3 Inclinometer pipedeep horizontal displacement test valuesof each grouting age

注浆深度/m不同注浆龄期测斜管变形/mm1h2h4h12h0.02.21.12.64.70.52.21.12.64.71.02.41.22.75.01.52.91.43.25.42.03.11.53.55.62.52.71.42.95.23.02.21.12.54.83.52.01.02.24.44.02.01.02.24.4

注：注浆深度为注浆加固土层(上覆土层不计入其中)顶面到测斜管倾斜监测点的距离

不同注浆龄期注浆段测斜管的变形相似，近似为二次抛物线，如图3所示。根据力与变形的关系可知，注浆龄期1 h，水泥-水玻璃双液注浆对埋设其中的测斜管施加一个初始正压力，方向与测斜管变形方向相同；注浆龄期2 h，压力减小，变形回弹；注浆龄期4 h，压力恢复，超过1 h龄期值，后续监测龄期压力持续增大。

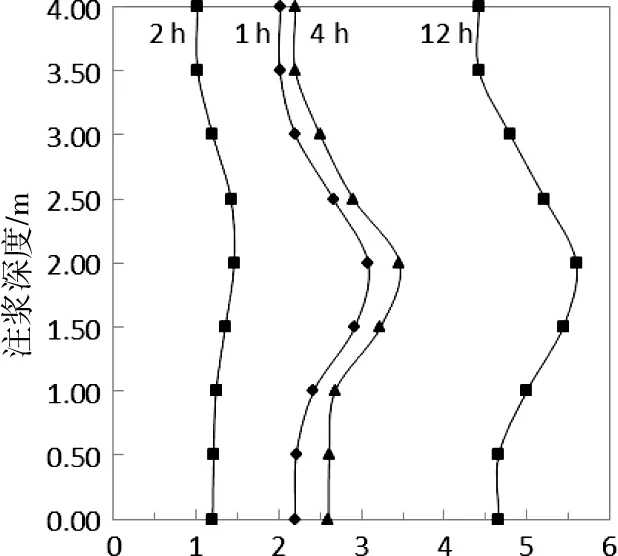
水平位移/mm图3　不同注浆龄期测斜管变形曲线Fig.3 Inclinometer pipe deformation curve of different grouting age

2.2水泥-水玻璃双液注浆不同注浆深度压力分布

水泥-水玻璃双液注浆范围2 m以外，测斜管变形很小，近似为零，因此测斜管力学计算的边界条件可以简化为注浆范围2 m以外的固端约束。水泥-水玻璃双液注浆示意图与边界条件简图如图4所示，试验测斜管由6061-T6铝合金制成，弹性模量E=67 620 MPa，泊松比μ=0.33。结合测斜管的边界条件与试验变形结果，根据力与变形的关系，利用有限元软件ABAQUS模拟当测斜管产生表3所示的变形时的内力如图5所示，不同注浆龄期各个注浆深度测斜管的内力Mises如表4所示，Mises是根据密塞斯(Von Mises)屈服准则计算的等效应力[13]，Mises的计算公式为：

(2)

式中：σ1，σ2，σ3为材料的第1，第2和第3主应力。

图4　水泥水玻璃双液注浆测斜管变形示意图Fig.4 Inclinometer pipe deformation schematic diagram of cement-silicate double solution grouting

单位：Pa图5　注浆龄期1 h测斜管变形应力Mises云图Fig.5 Mises stress nephogram due to inclinometer pipe deformation at grouting age of 1 h

Table 4 Mises stress finite element calculation results ofinclinometer pipeat different grouting age

注浆土层深度/m不同注浆龄期测斜管应力有限元计算结果/MPa1h2h4h12h0.03.871.914.618.300.51.910.851.333.571.02.641.013.401.381.52.481.582.194.242.05.121.926.559.262.52.021.471.423.103.02.421.123.021.463.51.930.863.274.624.03.521.763.847.75

根据表4作出不同注浆龄期测斜管内力Mises随注浆深度变化曲线图如图6所示。从图6可以看出，测斜管内力Mises沿注浆深度呈波浪形变化，没有明显规律可循，这是由土体局部的不均匀性引起的。总体来说，各个注浆龄期，Mises最大值出现在注浆土层中心深度；注浆龄期1，2和4 h，测斜管内力Mises最小值出现在注浆深度0.5 m附近，随着注浆龄期增大，测斜管内力Mises最小值向深层土体略微偏移，到注浆龄期12 h，Mises应力最小值出现在注浆深度1.0 m处。除去注浆加固中心深度所对应的Mises值，测斜管的第二大内力出现在注浆加固土层与未加固土层分界处。这说明，在注浆土体与未注浆土体的临界面，由于未加固土体的固端约束效应，使测斜管产生较大的内力；在注浆加固土体中心深度，由于水泥-水玻璃浆液大量聚集使测斜管产生最大变形，测斜管的等效应力Mises达到峰值。根据密塞斯(Von Mises)屈服准则，当Mises≥σs时，σs由单向拉伸实验确定)材料发生屈服破坏。因此，利用水泥-水玻璃双液注浆进行加固时，为防止材料屈服破坏，应对注浆土体中心深度和注浆土体与未注浆土体的临界面处的结构应力进行验算。

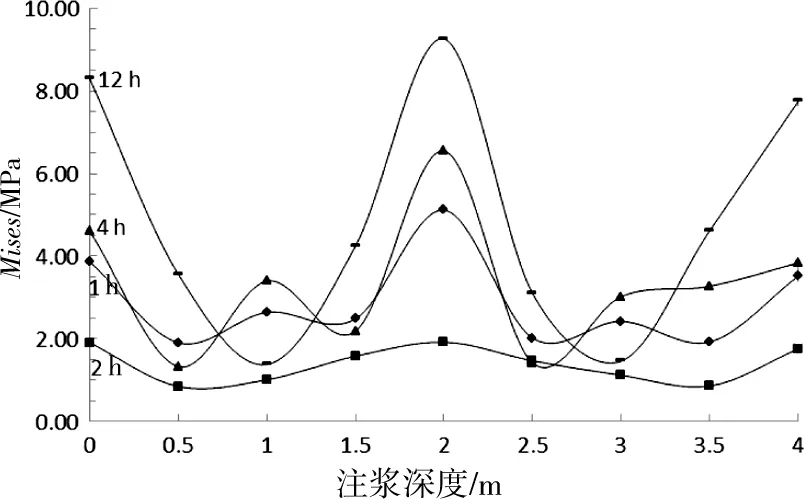
图6　不同注浆深度测斜管应力Mises变化曲线Fig.6 Inclinometer pipe Mises stress variation curve in different grouting depth

2.3水泥-水玻璃双液注浆对地下工程变形的影响

某基坑既有线下卧地铁盾构隧道注浆加固断面图如图7所示，地铁盾构隧道断面为圆环形，外径6.0 m，内径5.4 m，基坑基底标高为盾构隧道底部向下2 m，基坑边缘距离地铁盾构隧道中心12 m。由于两侧基坑土体开挖以及上部建筑材料堆积，地铁盾构隧道产生竖向压缩变形，使横截面水平直径线1-4方向尺寸变大，竖直方向尺寸减小，如图8所示。在盾构隧道外侧0.6 m进行水泥-水玻璃双液注浆，注浆土层为粉质粘土，注浆压强为0.4 MPa，浆液配比与测斜试验相同，注浆范围为地铁盾构隧道横截面水平直径线±2 m，如图7所示。

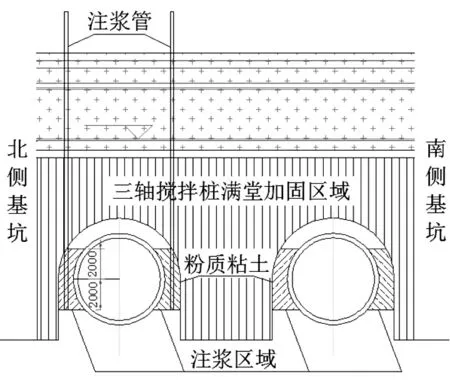
图7　地铁盾构隧道注浆断面图Fig.7 Grouting cross-section diagram of metro shield tunnel

图8　地铁盾构隧道变形监测图Fig.8 Deformation monitoring image of metro shield tunnel

注浆前后地铁盾构隧道1-4边累积变形曲线如图9～10所示。图9表明，水泥-水玻璃双液注浆前7 d地铁盾构隧道变形增大，最后趋于稳定，收敛值为9.20 mm。图10表明，水泥-水玻璃双液注浆1 h龄期，盾构隧道1-4边累积变形减小，7 h龄期变形回增，回弹量为0.1 mm，后续监测龄期1-4边累积变形持续减小，最后稳定在8.98 mm。结合图9～10可以看出，水泥-水玻璃双液注浆减少了地铁盾构隧道侧向变形，变化较小。对注浆龄期4 h的数据进行分析，注浆龄期4 h，盾构隧道的侧向变形减小了0.18 mm。由于盾构隧道直径为6 m，管片厚度为0.3 m，而其累积变形最大值只有9.2 mm，因此，根据小变形结构计算的基本假设，单纯分析水泥-水玻璃双液注浆对盾构隧道变形的影响时，可以看作盾构隧道是在原形尺寸的基础上发生了弹性变形δ。

δ=Δ0-Δt

(3)

式中：δ为由水泥-水玻璃双液注浆引起的盾构隧道变形，正值为径向压缩，负值为径向扩展；Δ0为注浆起始时间盾构隧道累积变形；Δt为注浆监测龄期盾构隧道累积变形。

地铁盾构隧道管片由高性能混凝土预制而成，弹性模量Ec=39 630 MPa，泊松比μ=0.17。注浆龄期4 h，由水泥-水玻璃双液注浆引起的盾构隧道应力分布有限元模拟如图11所示。由图11可以看出，水泥-水玻璃双液注浆对盾构隧道注浆区域中心部位施加的变形应力最大，这与测斜试验得出的结论吻合。由于地铁盾构隧道各向尺寸相等，与试验测斜管在空间形态、边界条件和力学简化上差别较大，因此测斜试验得出的加固土层与未加固土层临界处结构的应力分布规律不适用于该地铁盾构隧道。进一步分析，测斜试验得出的水泥-水玻璃双液注浆引起的结构内力分布规律与结构埋深较大，注浆土层临界面土体固端作用明显的结构的内力分布规律具有较好的拟合性。

图9　注浆前盾构隧道1-4方向累计变形曲线Fig.9 Accumulative deformation curve along 1-4 direction of shield tunnel without grouting

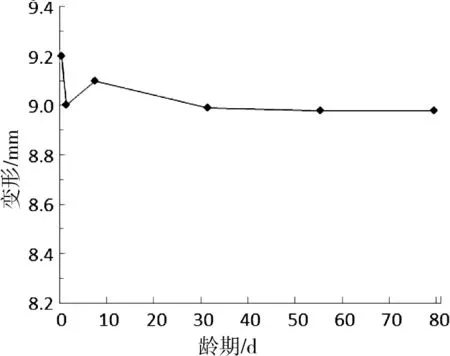
图10　注浆后盾构隧道1-4方向累计变形曲线Fig.10 Accumulative deformation curve along 1-4 direction of shield tunnel after grouting

单位：Pa图11　注浆龄期4 h盾构隧道应力Mises云图Fig.11 Mises stress nephogram of shield tunnel at grouting age of 4 h

3　结论

1)双液注浆填充了黏性土颗粒之间的孔隙，改变了原状土的固结特性，使土体注浆早期变得松散，后期强度增加，密实性变好；注浆龄期1 h，测斜管获得一个初始正压力，变形较大，2 h龄期压力部分卸载，变形减小，后续监测龄期变形持续增大。

2)各个注浆龄期，测斜管内力Mises最大值出现在注浆土层中心深度；注浆龄期1,2和4 h，测斜管内力Mises最小值出现在注浆深度0.5 m附近，随着注浆龄期增大，测斜管内力Mises最小值有向深层土体略微偏移的趋势，到注浆龄期12 h，Mises应力最小值出现在注浆深度1.0 m处。除去注浆加固中心深度所对应的Mises值，测斜管的第二大内力出现在注浆加固土层与未加固土层分界处。

3)水泥-水玻璃双液注浆减小了注浆侧地铁盾构隧道变形，变化值较小。由测斜试验得出的水泥-水玻璃双液注浆引起的结构内力的分布规律与结构埋深较大，注浆土层临界面土体固端作用明显的结构的内力分布规律具有较好的拟合性。

[1] 雷进生. 碎石土地基注浆加固力学行为研究[D].北京：中国地质大学，2013.

LEI Jinsheng. Research on mechanical behavior of grout in gravelly soil foundations[D]. Beijing: China University of Geosciences，2013.

[2] 尹筱琴. 基坑开挖对下部盾构隧道的影响研究[D]. 沈阳：东北大学，2011.

YIN Xiaoqin. Research on the influence of foundation excavation to lover tunnel segment[D]. Shenyang: Northeastern University，2011.

[3] 刘建茂，徐涛，康和勇，等. “双液注浆法”在基坑堵漏中的应用研究[J]. 地质找矿论丛，2008(1)：82-87.

LIU Jianmao，XU Tao，KANG Heyong，et al. Application research of double liquid grouting method in excavation leaking stopping[J]. Geological Prospecting Treatise，2008(1)：82-87.

[4] 李若飞. 地基注浆加固法在地铁盾构施工中对减少建筑物沉降的研究[D]. 包头：内蒙古科技大学，2015.

LI Ruofei. Study on reduction of building settlement by applying grouting foundation consolidation during subway shield construction[D]. Baotou: Inner Mongolia University of Technology，2015.

[5] 朱雯蕾. 厚卵砾漂石地层中注浆止水材料的研究与应用[D].北京:北京交通大学，2014.

ZHU Wenlei. Study and application of grouting material to water plugging for a thick gravel boulder formation[D].Beijing: Beijing Jiaotong University，2014.

[6] 苟长飞. 盾构隧道壁后注浆浆液扩散机理研究[D]. 西安：长安大学，2013.

GOU Changfei. Study on the grouts diffusion mechanism of shield tunnel back-filled grouts[D]. Xi'an: Chang'an University，2013.

[7] 杨志全，牛向东，侯克鹏，等. 宾汉姆流体柱-半球形渗透注浆形式扩散参数的研究[J]. 四川大学学报(工程科学版)，2015(增2):47-53.

YANG Zhiquan，NIU Xiangdong，HOU Kepeng，et al. Study on diffusion parameters of bingham fluid based on column-hemispherical penetration grouting[J].Journal of Sichuan University(Engineering Science Edition)，2015(Suppl 2):47-53.

[8] Dalmalm Thomas，Janson Thomas. Large-scale field investigation of grouting in hard jointed rock[J]. Geotechnical Special Publication，2003,12011:1628-1639.

[9] 王乾，曲立清，郭洪雨，等. 青岛胶州湾海底隧道围岩注浆加固技术[J]. 岩石力学与工程学报，2011(4)：790-802.

WANG Qian，QU Liqing，GUO Hongyu，et al. Grouting reinforcement techneque of qingdao jiaozhou bay subsea tunnel[J]. Chinese Journal of Rock Mechanics and Engineering，2011(4): 790-802.

[10] Jefferis Stephan A. Long term performance of grouts and the effects of grout by-products[J]. Geotechnical Special Publication，2003,12011:1141-1152.

[11] Anon. Ultrafine cement：A critical component of a grouting program[J]. Tunnels and Tunnelling International，2005,37(4):27-29.

[12] Groppo Sembenelli P, Sembenelli G. Deep jet-grouted cut-offs in riverine alluvia for ertan coffer dams[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999，125(2):142-153.

[13] 丁剑霆，刘海霞. 试论最大偏应力屈服准则与Mises、Tresca屈服条件的关系[J]. 黑龙江工程学院学报，2008(3):18-20.

DING Jianting，LIU Haixia. Study on the relationship between maximum deviatoric stress yield rule and Mises and Tresca yield conditions[J]. Journal of Heilongjiang Institute of Technology，2008(3):18-20.

Experimental study on mechanical characteristics of cement-silicate double solution grouting

WANG Xiaolong1，WANG Qicai1,2，ZHANG Rongling1,2，ZHANG Yakun3，WU Maoyin1

(1.School of Civil Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China;2.Road and Bridge Engineering Disaster Prevention Technology Laboratory of National and Local Joint projects，Lanzhou 730070，China;3.Road & Bridge Engineering Limited Company of China Railway No.21 Engineering Group，Xi'an 710000，China)

The experiment was carricd out by measuring high-precision inclinometer pipe deformation of 0.5 meter away from grouting center with grouting pressure 0.4 MPa and grouting age 1,2,4 and 12 h， and combining finite element software ABAQUS. The cement-silicate double solution grouting mechanical properties of different grouting age and different grouting depth was then studied. The results show：at grouting age of 1,2,4 and 12 h，the grouting force generated by cement-silicate double solution grouting increases at first, and then decreases and thereafter continually increase， with the minimum value appears at grouting age of 2 h；At different grouting age，the maximum inclinometer deformation stress Mises appears in central depth of grouting soil， and the second largest deformation stress of inclinometer appears in the critical position between grouting soil and no grouting soil.

cement-silicate double solution grouting；inclinometer pipe；grouting age；mechanical characteristics

2016-05-04

长江学者和创新团队发展计划滚动支持项目(IRT15R29)；国家自然科学基金资助项目(51268032)；陇原青年创新人才扶持计划项目

王起才(1962-)，男，河北晋州人，教授，博士，从事土木工程新材料及桥梁新结构的研究和开发；E-mail：13909486262@139.com

TU528.041

A

1672-7029(2016)10-1926-07