基于多主分量神经网络的同步DS-CDMA伪码盲估计
2016-11-11张天骐赵军桃江晓磊
张天骐,赵军桃,江晓磊
(重庆邮电大学信号与信息处理重庆市重点实验室,重庆 400065)
基于多主分量神经网络的同步DS-CDMA伪码盲估计
张天骐,赵军桃,江晓磊
(重庆邮电大学信号与信息处理重庆市重点实验室,重庆 400065)
针对批处理方法在实现非等功率同步直接序列码分多址(direct sequence code-division multiple access,DS-CDMA)信号伪码序列盲估计时存在的复杂度高、收敛速度慢的问题,引入了3种多主分量神经网络(Sanger NN、LEAP NN和APEX NN)。首先将已分段的一周期DS-CDMA信号作为神经网络的输入信号,用神经网络各权值向量的符号函数代表DS-CDMA信号各用户的伪码序列,然后通过不断输入信号来反复训练权值向量直至收敛,最终DS-CDMA信号各用户的伪码序列就可以通过各权值向量的符号函数重建出来。此外,本文提出了一种在递归最小二乘(recursive least square,RLS)意义下的最优变步长收敛模型,极大地提高了网络的收敛速度。理论分析与仿真实验表明:将3种神经网络用于同步非等功率DS-CDMA信号伪码盲估计时的复杂度均明显降低,且LEAP NN与Sanger NN均可有效地实现-20 dB信噪比、10个用户下的同步非等功率DS-CDMA伪码盲估计,APEX NN则相对较差,此外,LEAP NN消耗内存较大、收敛速度快,APEX NN相反,Sanger NN则介于两者之间。
盲估计; 码分多址; 伪码; 多主分量; 神经网络
0 引 言
直接序列码分多址(direct sequence code-division multiple access,DS-CDMA)信号是通过将多个携带有用信息的窄带信息码序列分别与多个高速伪码序列相乘再求和而获得的宽带扩频信号,因而其具有优良的抗干扰能力和低截获特性。然而,DS-CDMA系统中不可避免地存在的远近问题和多址干扰严重影响着这一技术的推广应用。第三代移动通信系统利用多用户检测技术来有效的解决这一问题,提高了这一信号应用的广泛性。目前,该信号已被广泛的应用于通信、雷达、遥感和遥控等领域。因此,研究该信号伪码序列的盲估计具有重要意义。
目前,针对DS-CDMA信号的伪码序列的盲估计已提出多种方法,如基于批处理(SVD或EVD)的方法[1],基于盲源分离的方法[2]以及基于子空间[3]的方法,但是批处理方法不可避免的会涉及到相关矩阵的R预先计算,具有计算复杂度高、收敛速度慢及计算存储量大等缺点,且当序列长度较长或工作于非平稳环境中时,该方法变得不再可行。而主分量神经网络可以自适应地进行模式识别与特征提取[4-5],且不需要进行R的预先计算,不涉及批处理运算,具有开销小、效率高、复杂度低等优点,因此得到了广泛的应用。文献[6]分别将主分量神经网络及奇异值分解(singular value decomposition,SVD)方法用于音频信号消噪,并对其性能进行了对比分析,但由于该文用到的神经网络为单主分量神经网络,因此并不适用于接收信号为DS-CDMA信号时的情况。然而,经典的Sanger神经网络[7-8]、通过主分量实现自适应特征提取的在线无监督学习(on line unsupervised learing neural network for adaptive feature extraction via principle component,LEAP)神经网络[9-11]以及自适应主分量提取(adaptive principle components extraction,APEX)神经网络[12-13]均为多主分量神经网络,且属于无监督检测,因此是一类很有潜力的非等功率同步DS-CDMA伪码盲提取工具。
本文利用多主分量神经网络复杂度低、效率高且可用于盲提取伪码序列的优良特性,将其用于非等功率同步DS-CDMA伪码序列的盲估计。另外,本文提出了一种在递归最小二乘[14-15](recursive least squares,RLS)意义下的最优收敛模型,极大地提高了网络的收敛速度。此外,本文网络仅需要已知伪码周期就可实现盲估计,由于已有大量文献可以求出同步DS-CDMA信号的伪码周期,如文献[16-17],所以本文假定伪码周期已知。本文首先引入Sanger NN、LEAP NN以及APEX NN,其次对各神经网络模型的收敛性及复杂度进行了详细分析,最后根据各神经网络能够收敛的最多用户数、最低信噪比以及相应的收敛速度进行了详细的仿真实验。理论分析与仿真实验表明,3种方法均可有效地实现较低信噪比与较多用户数条件下的非等功率同步DS-CDMA伪码序列盲估计,并且具有较好的收敛性能。
1 DS-CDMA模型
DS-CDMA信号可以简单的看作将K个性质类似的单用户DS-SS信号线性叠加而成的,一个有K个用户的基带数字DS-CDMA系统的接收信号可以表示为

(1)
(2)
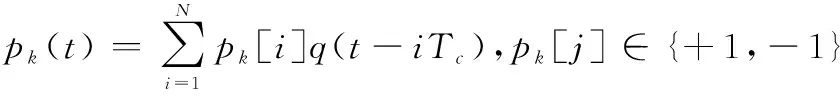
当τ1=τ2=…=τK=Tx时,式(2)代表了K个用户的同步DS-CDMA信号;而当τ1≠τ2≠…≠τK时,式(2)代表了K个用户的异步DS-CDMA信号。
本文只考虑非等功率的同步基带DS-CDMA信号。而且,不失一般性,取M=0,Tx=0,即每个用户每帧只有一个数据符号位。所以,本文所用到的接收信号模型可表示为
(3)
2 多主分量 NN方法
2.1Sanger NN、LEAP NN与APEX NN
根据Hebbian与Oja学习规则,Sanger提出了一种多主分量分析神经网络模型,如图1所示。
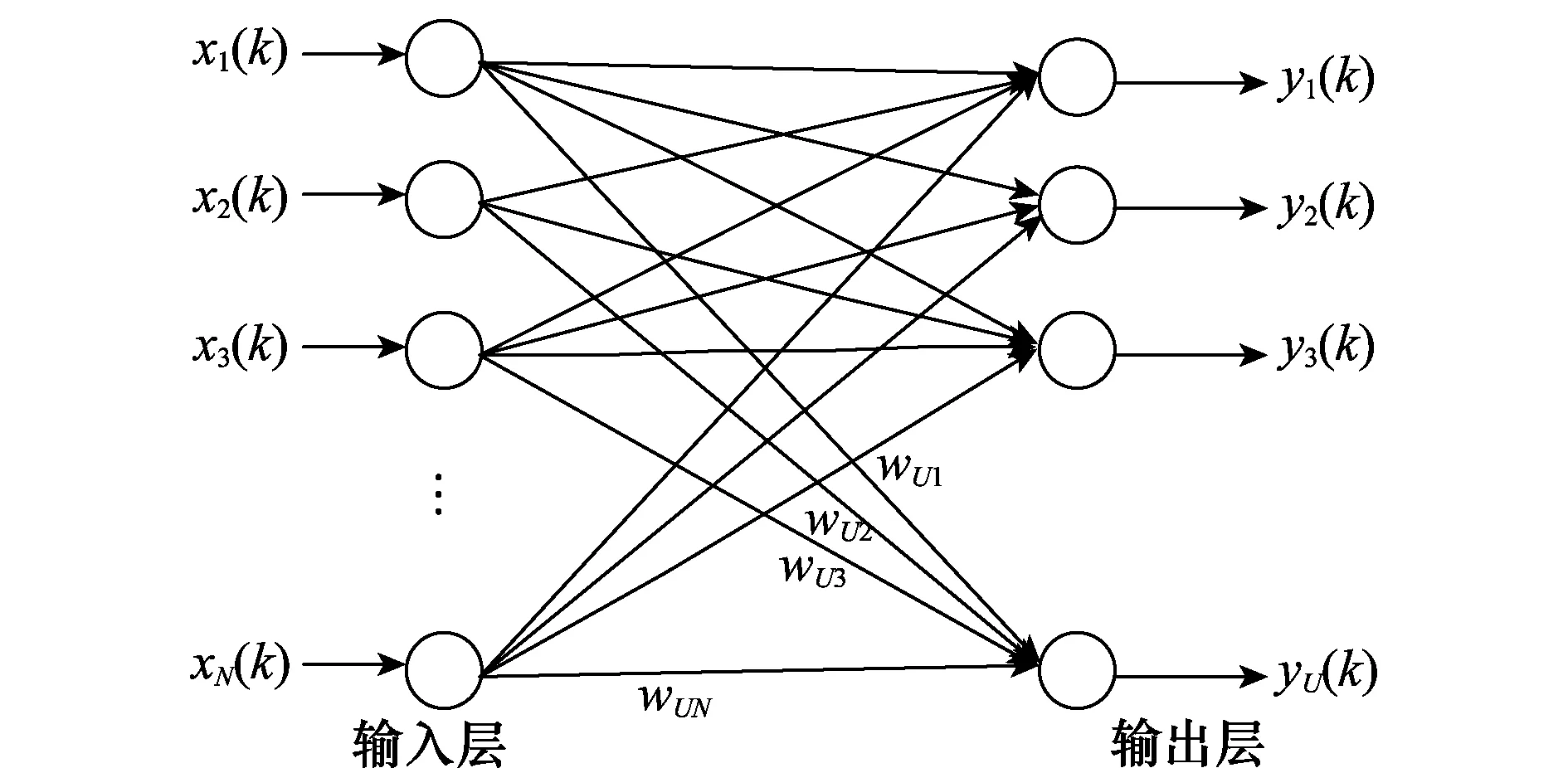
图1 Sanger 神经网络Fig.1 Sanger neural network

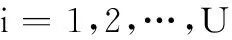
(4)
则由图1可得,输出为
(5)
式中,x(k)=[x1(k),x2(k),…,xN(k)]T;y(k)=[y1(k),y2(k),…,yU(k)]T,且权值更新公式为
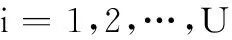
(6)
(7)
Chen H和Liu R W在Sanger NN的基础上提出了LEAP NN。其更新公式为下式给定的非线性、非自治动态差分方程:
(8)
式中
(9)
式中,I表示一个N×N的单位矩阵。在每次迭代时,Ai和Bi是所有连接权值中用于实现施密特正交化的去相关条件。当k→∞时,LEAP NN也可以提取任意大小的一组主分量。
根据反Hebbian规则(anti Hebbian rule)与Oja规则,Kung S Y提出了APEX NN。其特点是若给出前i-1个主分量,可用递推方式计算第i个主分量。APEX NN如图2所示,与Sanger NN的不同之处在于其在前向连接的基础上增加了用于使输出信号正交化去相关的侧向连接。
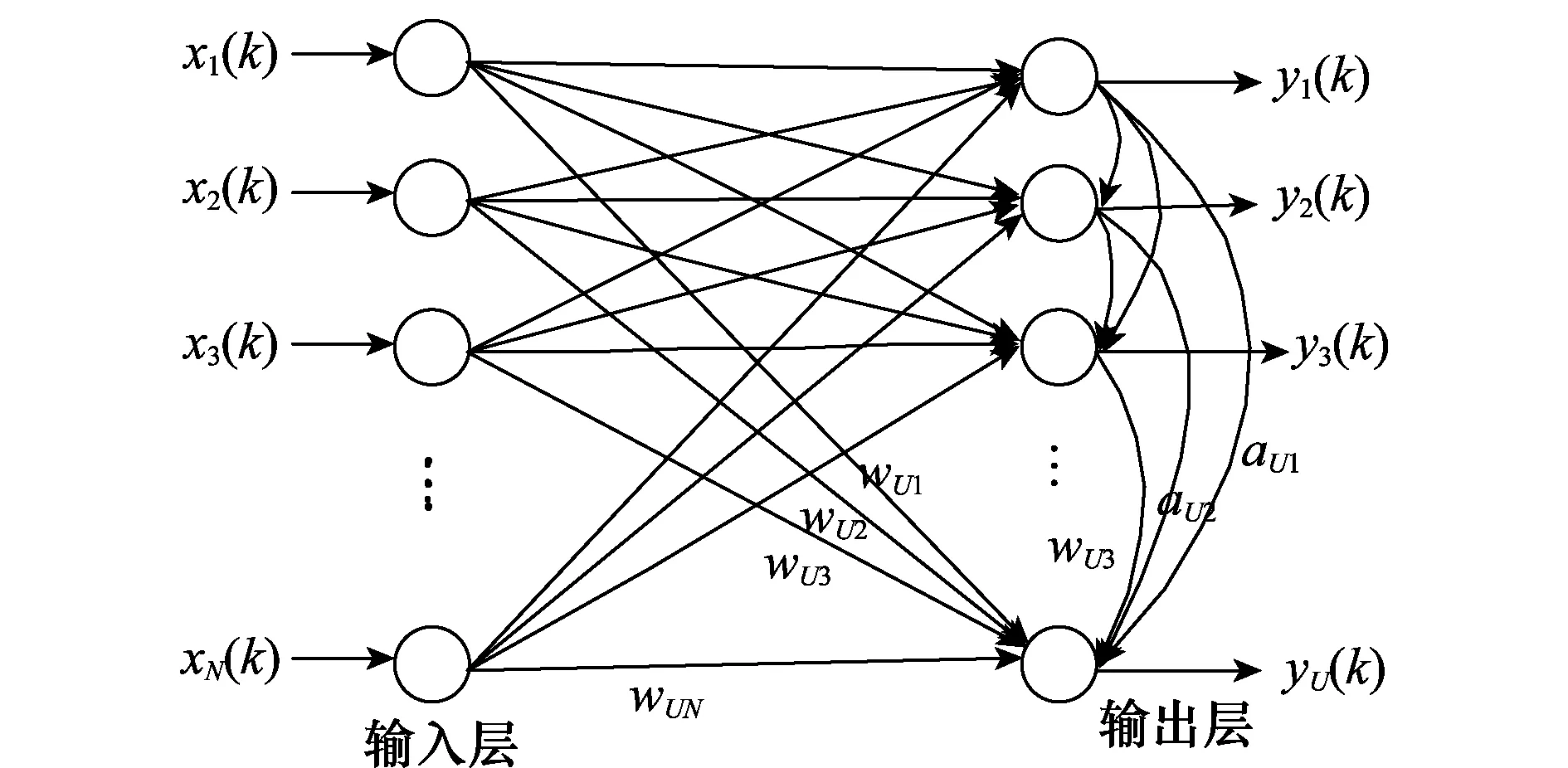
图2 APEX 神经网络Fig.2 APEX neural network
图2中各神经元均为线性神经元,其含有两种连接:前向连接、侧向连接。前向连接与Sanger NN中的wij(k)等效,它是按照一个Hebbian学习规则来工作的;侧向链接是指从输出神经元1,2,…,i-1,i=1,2,…,U到输出神经元i的连接,它将反馈应用到网络。这些连接被表示为反向权向量,即

(10)
侧向连接是按照一个反Hebbian学习规则来工作。由图2可知APEX NN的输入输出关系为
(11)
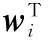
(12)
假设输入向量x(k)是来自于一个平稳过程,其自相关矩阵R具有互相区别的按降序排列的特征值,即
(13)
进一步假设图2中输出神经元1,2,…,i-1已经收敛到它们各自的稳定点,表示为
(14)
(15)
式中,ej是相关矩阵R的第j个特征值对应的特征向量,并且时刻k=0表示了网络的神经元i计算的起点,故此时式可以写为
(16)
式中,Q是一个(i-1)×N的矩阵,由相关矩阵R的前i-1最大特征值λ1,λ2,…,λi-1对应的特征向量e1,e2,…,ei-1构成,即
(17)
神经元i的前向权向量wi(k)和反向权向量ai(k)的更新等式分别定义为

(18)

(19)
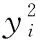
2.2Sanger NN、LEAP NN与APEX NN在RLS下的最优变步长学习速率
由于Sanger NN、LEAP NN与APEX NN的权值更新公式中均含有x(k)-yi(k)wi(k)项(特别地,对于APEX NN中的侧向连接,令ai(k)与wi(k)取相反的符号,则可得侧向权值增量中含有yi-1(k)-yi(k)ai(k)项,这将与x(k)-yi(k)wi(k)具有相同的形式),因此可令x(k)或yi-1(k)作为RLS算法中输入信号的期望信号,yi(k)作为RLS算法中的输出信号,wi(k)与ai(k)作为RLS算法的连接权值,以此来构建的RLS算法代价函数为
(20)
或
(21)
式中,0<γ≤1为遗忘因子,其作用是确保在过去某一段时间内的值被遗忘,从而使系统工作于平稳状态。
由代价函数推导得相应RLS算法的更新公式为
(22)
或
(23)
式中
(24)
由此,可得出3种多主分量神经网络在RLS意义下的最优变步长学习速率为
(25)
或
(26)
进一步可等效为
(27)
由文献[14]可知,d(0)是一个很小的正数,且由式(27)可知,初始值d(0)与γ值越小,变步长β(k)将越大,收敛速度越快。但是当d(0)与γ取值过小(尤其是γ过小)时,会导致收敛性不稳定,从而导致收敛速度变慢甚至不能收敛。
2.3Sanger NN、LEAP NN与APEX NN用于同步DS-CDMA信号伪码序列盲估计
当接收信号为式(3)给定的非等功率同步DS-CDMA信号时,假设Tx=0(已有文献可以求出Tx),将接收信号在不重叠的周期窗内采样,不失一般性,这里假设采样周期等于一个码片宽度,即采样周期为Ts=T0/N=Tc。则系统进行N次采样得到的一周期接收信号为
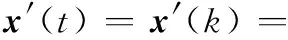
(28)
式中,{xi(t)=x[t-(i-1)Tc],i=1,2,…,N}是以采样周期Ts=Tc进行采样,即每切普一个采样点。在x′(t)输入神经网络之前,将其归一化为

(29)
式中
(30)
这样,主特征向量就会以一个较为鲁棒的形式估计出来。输出神经元的数量U等于所需主分量的个数(在本文中等于DS-CDMA信号用户的个数),通常取U≤N。在许多“降维”的实际应用中U≪N。通过网络权值的反复更新,最终权值将收敛于DS-CDMA信号的伪码序列。另外,为了使该神经网络取得更好的收敛性能,本文采用式(27)所给定的变步长。
3 收敛性分析
3.1数学等价模型
现以APEX NN为例(其他两种网络的数学等价模型推导与其相似)。为了获得一个实际中易于处理的数学模型,利用Ljung L提出的随机估计算法收敛性分析工具,本文可以应用两种近似:存在足够大的正整数M,充分小的正常量β,使得:
(31)
(32)
(33)

(34)
和
(35)
进一步,可以用{k,k+1,k+2,…}来代替{k,k+M,k+2M,…},式(34)与式(35)就可以简化为下式:
(36)
(37)
式中,γ=Mβ,此时的wi(k)、ai(k)是M个时刻的瞬时权值的平均值。这是非常关键的一步,因为通过上述等价,前面的非线性、非自治动态差分方程就可以近似为非线性、自治确定性差分方程。一般来说,两个系统的渐进轨迹是等价的,即其中一个系统收敛就意味着另一个系统也收敛。
同理,可推导得Sanger NN非自治动态系统的自治确定性系统数学等价模型为
(38)
LEAP NN非自治动态系统的自治确定性系统数学等价模型为
(39)
3.2i=1时的收敛性分析
对于Sanger NN,当i=1时,有
(40)
这里,将连接权值向量w1(k)按照相关矩阵的正交归一化特征向量集展开如下:
(41)
式中,ej是矩阵R的特征值λj对应的特征向量;θ1j(k)是展开时的时变系数,则有
(42)
(43)
利用定理1可得
(44)
定理1(证明见文献[9])已知
(45)
则有
(46)
3.3i≠1时的收敛性分析
当i≠1时,利用归纳法,首先假设输出神经元1,2,…,I-1,I>1已经收敛到它们的稳定状态,然后证明在假设条件下第I个神经元也能收敛。接下来分别证明3种多主分量神经网络在i≠1时的收敛特性。
3.3.1Sanger NN的收敛性分析

3.3.2LEAP NN的收敛性分析
现取i=I,则有
(47)
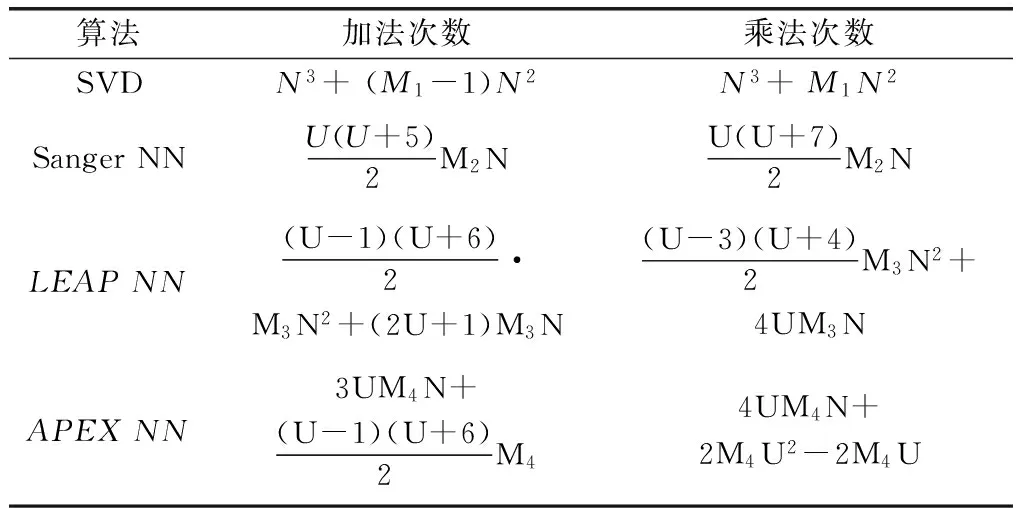
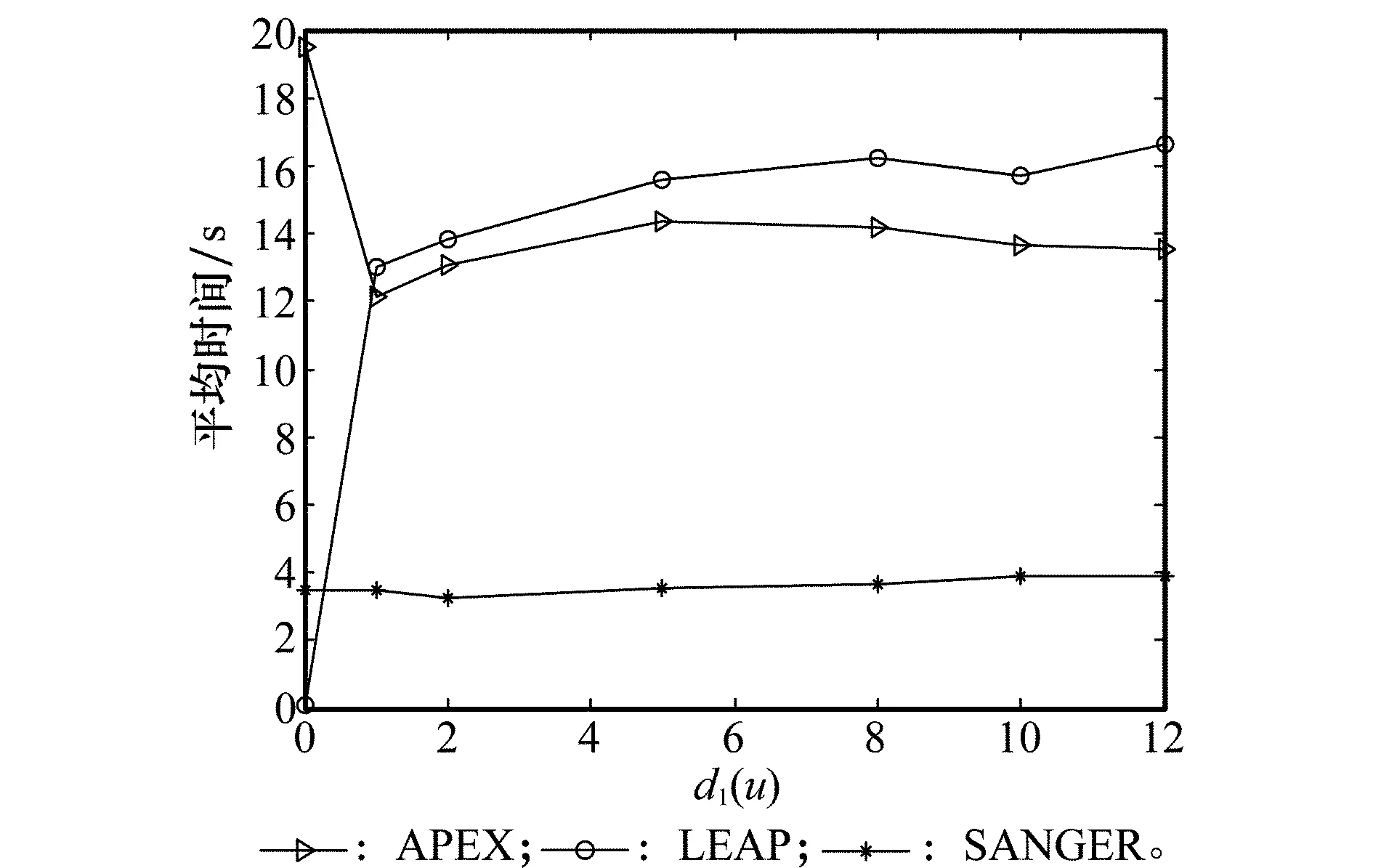
令εl(k)=wl(k)-el∈RN,l=1,2,…,I-1,则由假设可得存在常量c>0,0 (48) 则有 (49) 其中 (50) (51) 显然所有ΦI(k)∈RN×N的绝对值有一致的上界3(I-1)cdk,其值当k→∞时,以指数形式收敛于0。现设ΨIi(k)是ΦI(k)ei到向量ei上的映射,则当k→∞时,其值也以指数形式收敛于0。因此,式可以简化为 (1)当1≤j≤I-1时 (52) (2)当I≤j≤N时 (53) 利用定理2可得: (54) 定理2(证明见文献[9])已知: (55) 则有 (56) 3.3.3APEX NN的收敛性分析 现取i=I,且令其前向连接权值向量按式展开,接着用基本关系式: Rej=λjej (57) 来表达矩阵积RwI(k)如下: (58) 类似地,用式(17),可以将矩阵积RQTaI(k)表达为 (59) 式中,A=[aI1(k),aI2(k),…,aII-1(k)]。因此,将式(59)代入式(36),并简化,得 (60) 同理,反向权向量aI(k)的更新等式(37)可以被转化为 (61) 式中,1j是除了第j个元素等于1,其他所有I-2个元素都为零的向量;下标j被限制在1≤j≤I-1。 有两种情况需要被考虑(依赖于下标j以及I-1的分配值)。下文情形1表示的1≤j≤I-1,其涉及该神经网络“老”主模式的分析;情形2表示的I≤j≤N,其涉及该神经网络“新”主模式的分析。 情形 1当1≤j≤I-1时,在这种模式下,由式(60)和式(61)可得: (62) (63) 用矩阵形式,可以将式(62)和式(63)变换为 (64) 式中 则式(64)描述的系统矩阵的特征值如下: (65) 从式(65)中,能够得出两个重要的结论: (1)在式(65)中矩阵系统的特征值ρIj是独立于相关矩阵R的所有特征值λj。 给定ρIj<1时,式(48)的展开式系数θIj(k)和反向权向量aIj(k)将对所有的k以相同的速度渐进的趋于零,因为网络所有的主模式都具有相同的特征值。这个结果是相关矩阵特征向量的正交归一化性质的一种延续。换句话说,wI(k)按照相关矩阵R的整个归一化特征向量集的展开式是式所描述结果的基础,特征值λj的选择是不变的。 情形 2当I≤j≤N时,在这种情况中,反向权向量aIj(k)对网络节点没有影响,表示如下: (66) 因此,对每一个主模式I≤j≤N,有一个简单的等式如下: (67) 其直接从式(60)和式(66)推导得到。根据情形1,对1≤j≤I-1,θIj(k)和aIj(k)将最终收敛到零。且神经元输出的平均输出功率为 (68) 这里设θII(k)≠0,且定义 (69) 可以接着将式(69)写为 (70) 由自相关矩阵的特征值λI>λj,I (71) 因此 (72) 故 (73) 此时,式(68)可以简化为 (74) 并且由式(67)可得 (75) 推导得 (76) 这个极限条件就暗示了以下双重含义 (1)从式(48),有 (77) (2)从式(74),有 (78) 换言之,当k迭代次数趋于无穷大时,图2所示的神经网络将提取出输入向量x(k)相关矩阵R的第I个特征值及对应的特征向量。这当然是首先假设了神经网络的神经元1,2,…,I-1已经收敛到了相关矩阵R的特征值及其对应的特征向量,这就证明了APEX NN在i≠1时收敛性。至此,Sanger NN、LEAP NN与APEX NN的收敛性就证明完毕。 此外,这里对3种多主分量神经网络分析时按照“串行模式”处理,即,第i个神经元是在前i-1个神经元已经收敛后才开始工作。这样做的目的仅是为了以一种简单的方式来解释网络的工作原理。然而,实际上,各网络结构均是按照“并行模式”工作的,即各网络中的神经元均是趋向于同时收敛。 算法的时间复杂度一般是指算法实现过程中用到的乘法次数与加法次数。本文取用户数为U,伪码序列长度为N(本文中等于输入神经元个数),各算法达到收敛时所需的信息码元数(本文中等于算法收敛所需要的数据组数)分别为M1,M2,M3,M4,且一般来说M1,M2,M3,M4各不相等,则各算法的单次蒙特卡罗实现所需的复杂度如表1所示。 表1 复杂度分析 由表1可知,若不考虑M1,M2,M3,M4对各算法复杂度的影响,当U=1时,Sanger NN、LEAP NN与APEX NN的计算复杂度相同,这是因为此时3种神经网络结构相同;当U≠1时,LEAP NN复杂度最大(因为其结构中包含矩阵运算),Sanger NN次之,APEX NN最小。对于批处理方法来说,其复杂度与用户数无关,且一般有U≪N,因此其复杂度远大于多主分量神经网络的方法。 实验说明:以下实验主要针对非等功率同步DS-CDMA信号。 (1)非等功率同步DS-CDMA信号各用户的PN序列是长度为100 (或200)位的截断m序列,序列的幅度为±1。 (2)每个用户每次均匀随机地产生幅度为±1的一位信息码,然后用它们分别去调制对应用户的PN码。 (4)实验中用到的信噪比为 (79) (80) (81) 式中,Var{·} 表示求方差操作;SNRk表示第k个用户的信噪比;SNRavr 、SNRsum分别为所有用户的平均信噪比和总的信噪比。 (5)本文各实验均取蒙特卡罗次数为Mncr=200,上采样次数为Sa=1,算法达到收敛时允许存在1%的误码率。 (6)本文实验2到实验5是在式(27)所示的变步长环境下进行,其中d(0)的初始值取10.0,参数γ取恒定值0.995。 实验 1确定各算法变步长的最优初值以及初步比较3种算法达到收敛时所需的平均数据组数与平均实际时间。 这里取PN码长为100,用户数为7,噪声标准差σV=5。图 3和图4是取γ=0.99,d(0)=[eps,1,2,5,8,10,12]时所得实验结果图。而图5和图6是取d(0)=1.0,γ=[0.98 0.9850.990.9950.998]时得到的实验结果图。 图3 初值对收敛数据组数的影响Fig.3 Influence of the initial value on the number of convergence data sets 图4 初值对收敛时间的影响Fig.4 Influence of the initial value on convergence time 由图3和图4可知,当取d(0)=0时,LEAP NN达到收敛时所需数据组数几乎为零,事实上,这是由于此时收敛已不稳定,误码率收敛到NaN所致,且对于APEX NN,此时的收敛性能也较差。当d(0)≠0时,随着初值的增大,收敛性略微变差,但效果不明显,可见当初值d(0)在一定范围内时,收敛速度对d(0)并不敏感。此外,就神经网络达到收敛时所需的平均数据组数而言,LEAP NN性能最好,Sanger NN性能次之,APEX NN性能最差;就神经网络达到收敛时所需的实际平均时间而言,Sanger NN性能最好,APEX NN性能次之,LEAP NN性能最差(这是由于LEAP NN引入了矩阵结构使得运算量增大)。 图5 遗忘因子对收敛数据组数的影响Fig.5 Influence of the forgetting factor on the number of convergence data sets 图6 遗忘因子对收敛时间的影响Fig.6 Influence of the forgetting factor on convergence time 由图5和图6可知,当取γ<0.98时,3种神经网络已经不能收敛(或收敛性能很差),故文中不予考虑。当取γ≥0.98,神经网络达到收敛时所需的平均数据组数与平均实际时间随γ的变化曲线大致呈“凹”形,这与前面的理论描述相一致。 为了方便对比分析,本文以下各实验统一取d(0)=10.0,γ=0.995。 实验 2比较APEX NN、LEAP NN以及Sanger NN在低信噪比条件下的收敛性能(这里仅考虑平均数据组数,下同)。 本实验中取PN码长度为100位,用户数为7。则3种神经网络在不同信噪比下收敛性能如表2所示。其中表2中σV代表噪声的标准差,a=SNRavr,b=SNR7分别代表相应噪声条件下的平均信噪比与第7个用户(该用户的功率最小)的信噪比。 由表2可知,当σV≥9时,由于信噪比太低而导致算法收敛所需数据组数太大或不能收敛。且随着信噪比的降低,各算法达到收敛所需的平均数据组数都在逐渐增加。此外,在相同的信噪比条件下,LEAP NN的收敛性能最好,Sanger NN次之,APEX NN最差。 表2 在不同信噪比下的平均数据组数 实验 3比较APEX NN、LEAP NN以及Sanger NN在多用户情况下的性能。 这里取PN码长度为100位,σV=0.5,其中用户数分别取U=7,8,9,10,11,且其相应的幅度值分别为 则3种神经网络在用户数分别取7,8,…,11时的收敛性能如表3所示,表3中U代表用户数,a=SNRavr,bk=SNRk,k=7,8,…,11分别代表相应用户数条件下的平均信噪比与第k个用户的信噪比。 表3 在不同用户数下的平均数据组数 由表3可知:当U≥11时,由于信噪比太低而导致算法收敛所需数据组数太大或不能收敛。且随着用户数的增加,各算法达到收敛所需的平均数据组数在逐渐增加。此外,在相同的用户数条件下,LEAP NN的收敛性能最好,Sanger NN次之,APEX NN最差。此外,如果σV值减小,相应的信噪比会增大,用户达到收敛所需要的平均数据组数会进一步减小,可以收敛的用户数也会增多。 实验 4分析APEX NN、LEAP NN以及Sanger NN在不同伪码长度时的性能。 本实验中取用户数为7,则3种神经网络在伪码长度取100、200位时的均值收敛性能如图7所示。 由图7可知,当PN序列长度为200时,各算法达到收敛所需平均数据组数明显小于PN序列长度为100时,即PN序列越长,收敛性能越好。此外,随着信噪比的降低,各算法达到收敛所需的平均数据组数都在逐渐增加。而且,在相同信噪比条件下,LEAP NN的收敛性能最好,Sanger NN收敛性能次之,APEX NN的收敛性能最差。 图7 不同伪码长度下的均值性能曲线Fig.7 Average performance curve under different PN length 实验 5分析APEX NN、LEAP NN以及Sanger NN各个用户的平均比特误码率与平均数据组数。 这里取用户数为7,PN码长度为C=100,则3种神经网络提取信号前3个用户时的学习收敛曲线如图8所示,均值性能曲线如图9所示。 图8 学习收敛曲线Fig.8 Learning convergence curve 图9 均值性能曲线Fig.9 Mean performance curve 由图8可知,各算法的平均误码率都随着输入信号数据组数的增加而减小,且在相同的条件下,第一个用户的伪码序列在刚开始估计时收敛速度明显快于其他用户,这是由于第一个用户的信号强度最大的缘故。 由图9可知,在相同条件下第一个用户的伪码序列估计所需数据组数明显小于其他用户,这同样是由于第一个用户的幅度值最大的缘故。 其中曲线不够平滑是因为蒙特卡罗次数较少的缘故,且相互交叉的曲线并不存在直接比较。 本文通过3种多主分量神经网络权值向量的符号函数来重建非等功率同步DS-CDMA信号各用户的伪码序列,从而实现该信号伪码序列的盲估计。本文提供了一种在RLS意义下的最优变步长收敛模型,极大地提高了算法的收敛速度。通过理论分析与仿真实验得出,相比于批处理方法,3种多主分量神经网络在实现非等功率同步DS-CDMA信号伪码盲估计时的复杂度均明显降低,且APEX NN的复杂度最低,Sanger NN次之,LEAP NN最高。在允许1%的误码率条件下,当用户数为7时,3种多主分量神经网络都可以有效地实现在最小用户信噪比为-27.9 dB下的非等功率同步DS-CDMA伪码序列的盲估计;当噪声标准差为σv=0.5时,Sanger NN与LEAP NN可以有效地实现10个用户的非等功率同步DS-CDMA伪码序列的盲估计,APEX NN则性能较差;此外,就算法达到收敛时所需的平均数据组数而言,LEAP NN性能最好,Sanger NN性能次之,APEX NN性能最差;就算法达到收敛时所需的实际平均时间而言,Sanger NN性能最好,APEX NN性能次之,LEAP NN性能最差。另外,由于本文神经网络能够自适应地处理输入数据且不需要存储权值更新的中间变量,因此可以工作于输入数据无限长以及非平稳的环境中。 [1] Luo Z,Zhu L.A charrelation matrix-based blind adaptive detector for DS-CDMA systems[J].Sensors,2015,15(8):20152-20168. [2] Wu W J,Zhang T Q,Shi S,et al.Parallel blind estimate of spreading sequences in multi-rate DS/CDMA signals[J].Information and Control,2015,44(2):171-178.(吴旺军,张天骐,石穗,等.多速率DS/CDMA信号扩频序列并行盲估计方法[J].信息与控制,2015,44(2):171-178.) [3] Zhou L,Leung H,Xu P,et al.The Kalman filtering blind adaptive multi-user detector based on tracking algorithm of signal subspace[J].Information,2015,6(1):3-13. [4] Bouzid A,Ellouze N.Speech enhancement based on wavelet packet of an improved principal component analysis[J].Computer Speech and Language,2016,35:58-72. [5] Bai D,Liming W,Chan W,et al.Sparse principal component analysis for feature selection of multiple physiological signals from flight task[C]//Proc.of the IEEE International Conference on Control Automation and Systems,2015:627-631. [6] Nie Z G,Zhao X Z.Similarity of signal processing effect between PCA and SVD and its mechanism analysis[J].Journal of Vibration and Shock,2016,35(2):12-17.(聂振国,赵学智.PCA与SVD信号处理效果相似性与机理分析[J].振动与冲击,2016,35(2):12-17.) [7] Sanger T D.Optimal unsupervised learning in a single-layer linear feedforward neural network[J].Neural Networks,1989,2(6):459-473. [8] Zhang T Q.Blind processing for signal of direct sequence spread spectrum[M].Beijing:National Defence Industy Press,2012:195-196.(张天骐.直扩信号的盲处理[M].北京:国防工业出版社,2012:195-196.) [9] Chen H,Lin R W.An on-line unsupervised learning machine for adaptive feature extraction[J].IEEE Trans.on Circuits and Systems-II:Analog and Digital Signal Processing,1994,41(2):87-98. [10] Zhang T Q,Chen Q B,Zhou Z Z,et al.Adaptive feature extraction of lower SNR DS-CDMA signals[C]//Proc.of the IEEE International Conference on Signal Processing,2006. [11] Zhang T Q,Dai S S,Li X S,et al.A neural network method to adaptive feature extraction of weak DS-CDMA signals[C]//Proc.of the IEEE Congress on Image and Signal Processing,2008:385-389. [12] Kung S Y,Diamantaras K I,Taur J S.Adaptive principal component extraction (APEX)and applications[J].IEEE Trans.on Signal Processing,1994,42(5):1202-1217. [13] Zhang T Q,Tian Z S,Chen Q B,et al.Use APEX neural networks to extract the PN sequence in lower SNR DS-SS signals[J].Lecture Notes in Computer Science,2006,4114:1252-1257. [14] Hong X,Gong Y.A constrained recursive least squares algorithm for adaptive combination of multiple models[C]//Proc.of the IEEE International Joint Conference on Neural Networks,2015:1-6. [15] Hunki K,Shaheen E M,Soliman M,et al.Blind adaptive LMS multiuser detector with variable step size[C]//Proc.of the IEEE International Conference on Engineering and Technology,2014:1-5. [16] Zhang T Q,Zhou Z Z,Kuang Y J,et al.New method for periodic estimation of the PN sequence in the lower SNR long code DS-SS signals[J].Systems Engineering and Electronics,2007,29(1):12-16.(张天骐,周正中,邝育军,等.低信噪比长伪码直扩信号伪码周期的估计方法[J].系统工程与电子技术,2007,29(1):12-16.) [17] Wu W J,Zhang T Q,Yang R,et al.Blind periodic estimate of PN sequence based on reprocessing of power in multirate DS/CDMA transmissions[J].Telecommunication Engineering,2014,54 (7):937-944.(吴旺军,张天骐,阳锐,等.利用二次谱盲估计多速率DS/CDMA伪码周期[J].电讯技术,2014,54(7):937-944.) PN code sequence blind estimate of synchronous DS-CDMA based on multi-principal component neural network ZHANG Tian-qi,ZHAO Jun-tao,JIANG Xiao-lei (Chongqing Key Laboratory of Signal and Information Processing,Chongqing University of Posts and Telecommunications,Chongqing 400065,China) Aiming at the problem of the batch processing method with high complexity and slow convergence speed for the pseudo-noise (PN)code sequence blind estimate of synchronous direct sequence code-division multiple access (DS-CDMA)signals under different power level,three multi-principal component neural networks (NNs)are introduced—Sanger NN,LEAP NN and APEX NN.Firstly,the period segmented DS-CDMA signals are chosen as the neural network input and the symbol function of each weight vector is used to represent the PN code sequence of each user.Then through the continuous input signal,the weight vectors of the NN are trained repeatedly until convergence.Finally,the PN code sequence of each user can be rebuilt by the symbolic function of each weight vector.Furthermore,an optimal variable step convergence model is put forward via the recursive least square (RLS),which improves the convergence speed of the network greatly.Theory analysis and simulation results show that the complexity of three kinds of NNs when used to the PN code sequence blind estimate of synchronous DS-CDMA signals under different power level is reduced significantly,and when the signal to noise ratio (SNR)is -20 dB and the number of users is 10,the PN code sequence of synchronous DS-CDMA signals under different power level can still be estimated by LEAP NN and Sanger NN efficiently.Compared with LEAP NN and Sanger NN,APEX NN is poor relatively.In addition,LEAP NN consumes lager memory but it has fast convergence speed.APEX NN is contrary to LEAP NN; Sanger NN is between the LEAP NN and the APEX NN. blind estimate; code division multiple access (CDMA); pseudo-noise (PN)code; multi-principal component; neural networks (NNs) 2016-01-25; 2016-07-05;网络优先出版日期:2016-08-16。 国家自然科学基金(61671095,61371164,61275099);信号与信息处理重庆市市级重点实验室建设项目(CSTC2009CA2003);重庆市教育委员会科研项目(KJ130524,KJ1600427,KJ1600429)资助课题 TN 911.7 ADOI:10.3969/j.issn.1001-506X.2016.11.27 张天骐(1971-),男,教授,博士研究生导师,博士,主要研究方向为扩频信号的盲处理、神经网络实现以及信号的同步处理。 E-mail:zhangtq@cqupt.edu.cn 赵军桃(1991-),男,硕士研究生,主要研究方向为基于神经网络的直扩信号盲处理。 E-mail:1012928803@qq.com 江晓磊(1992-),女,硕士研究生,主要研究方向为导航信号的捕获与跟踪。 E-mail:173993170@qq.com 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160816.1504.002.html
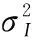
4 复杂度分析
5 仿真实验
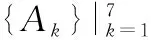

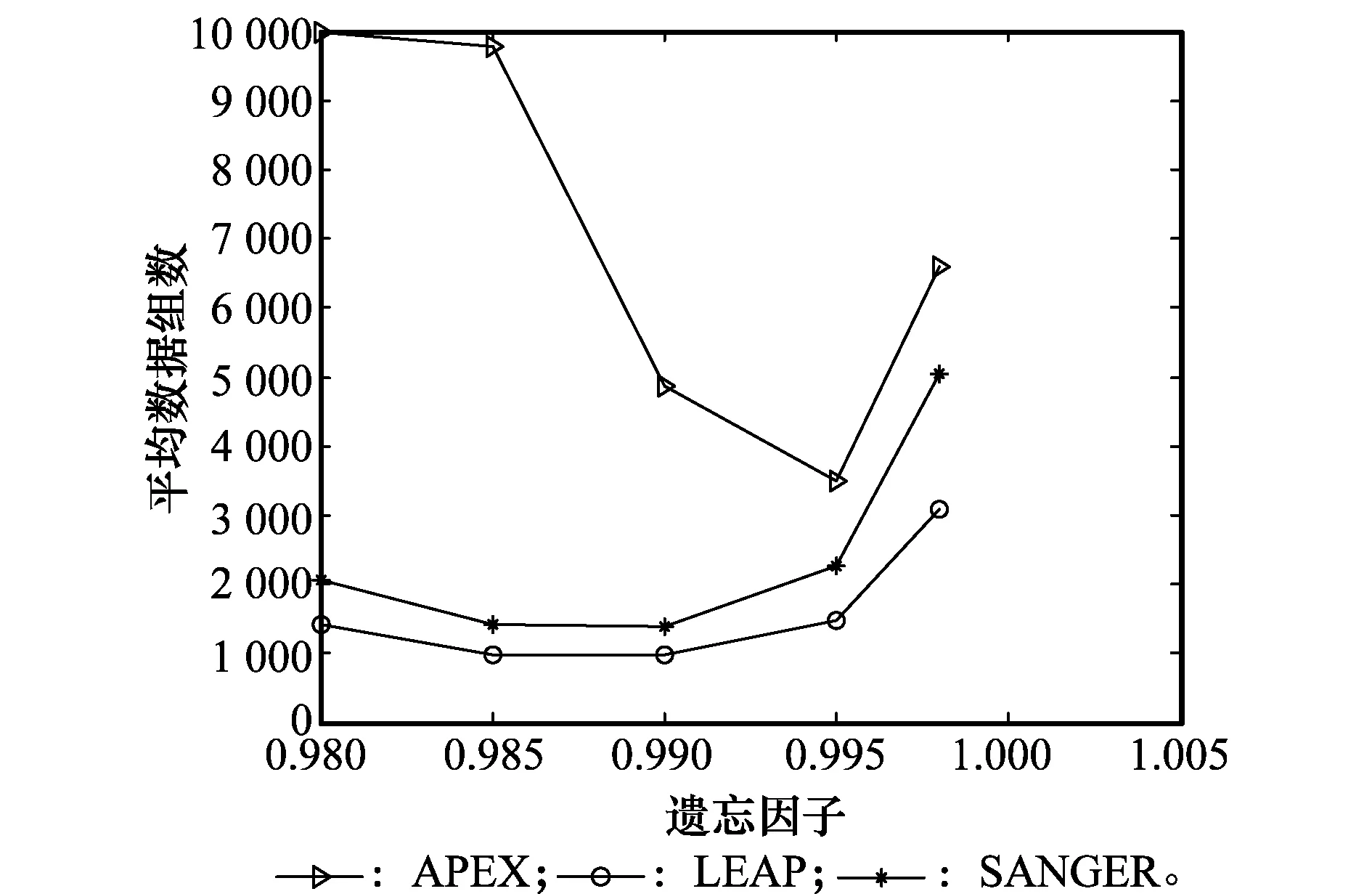
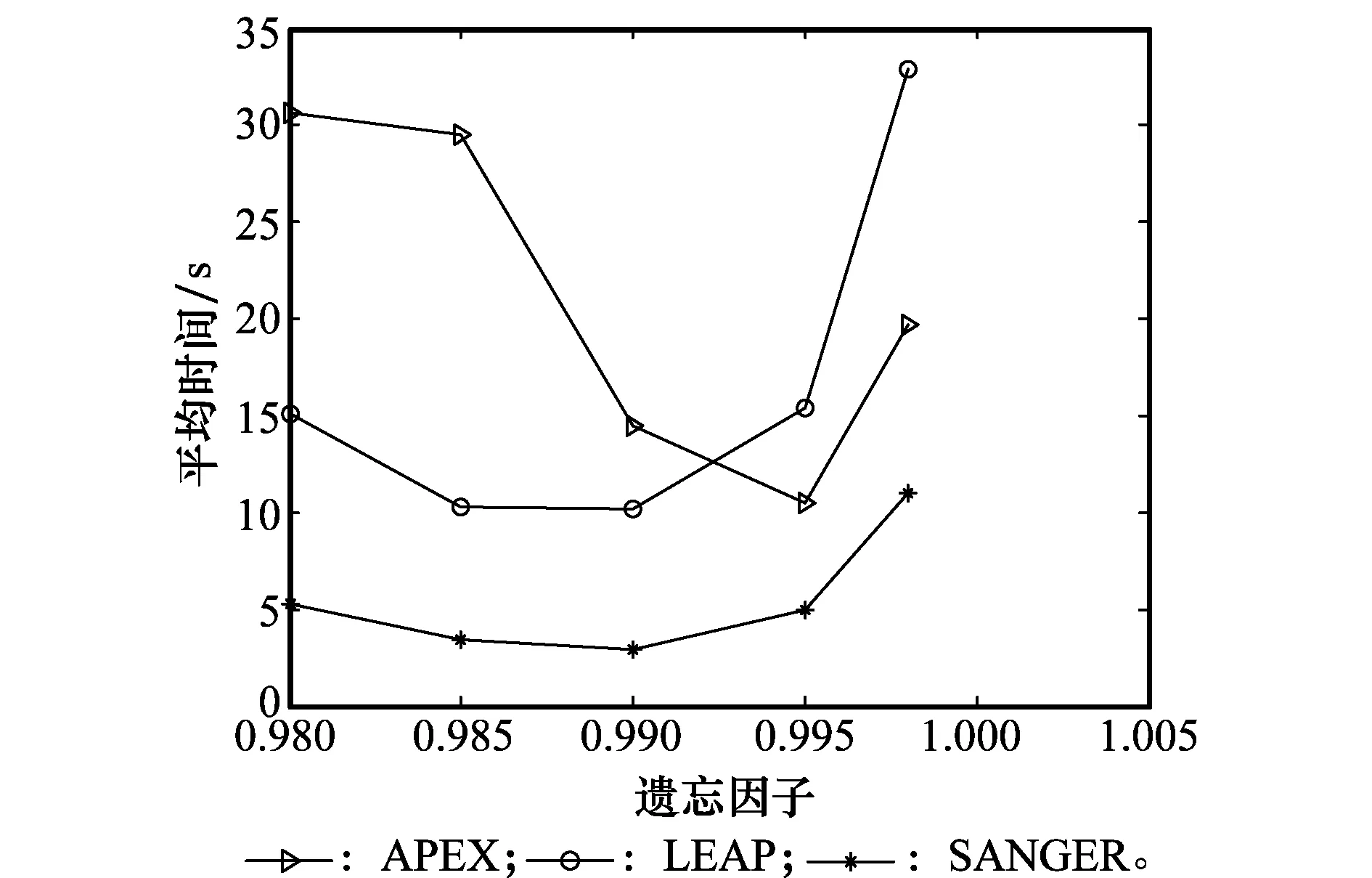



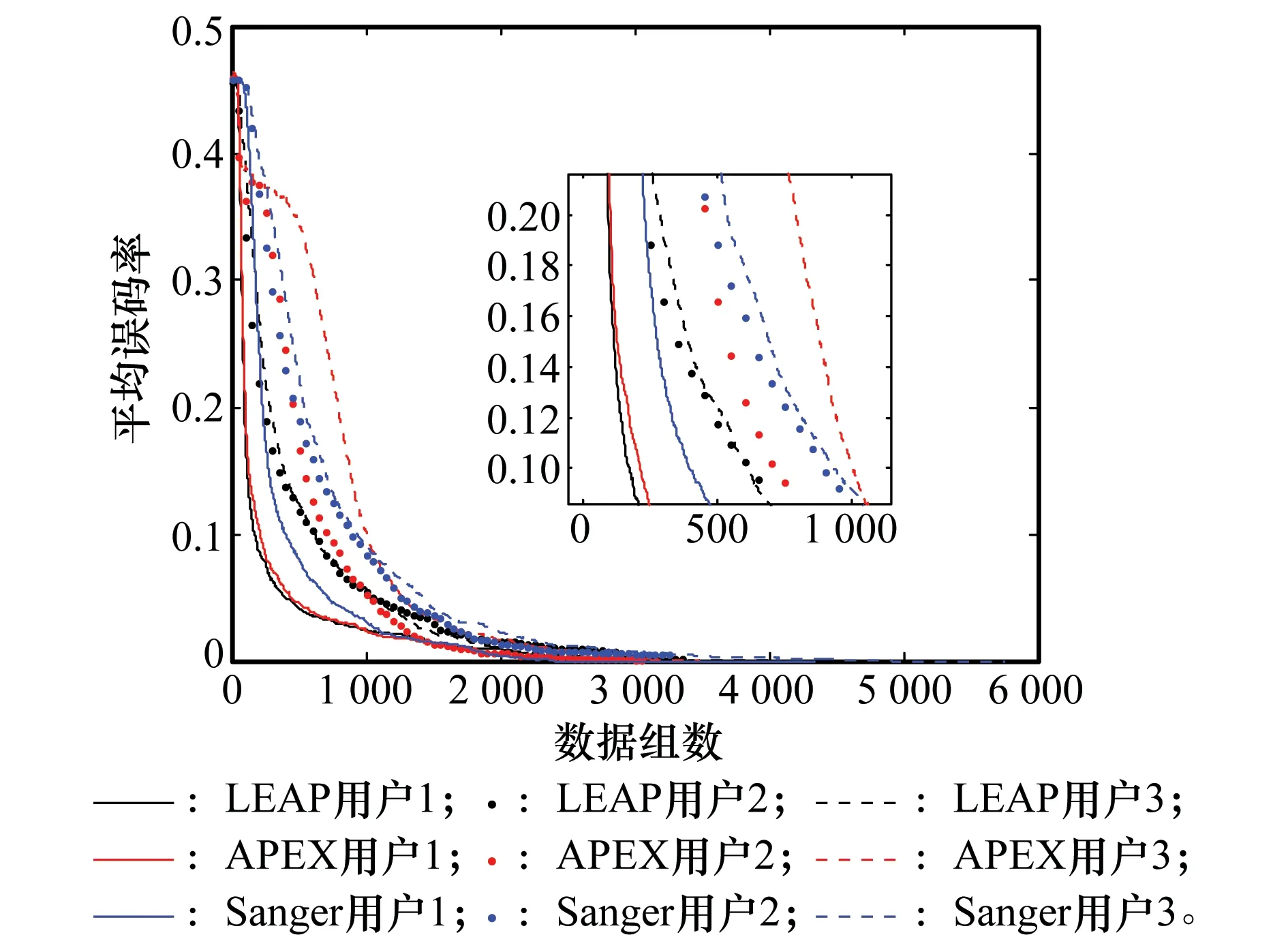
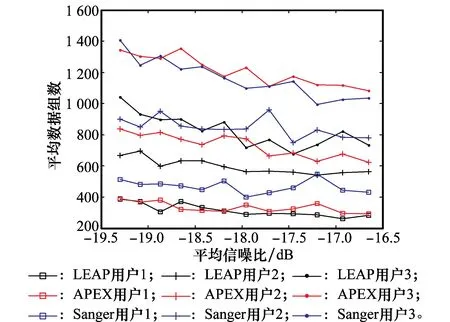
6 结 论
