双系统合作式协同进化算法求解不可分解函数
2016-11-11崔锋哲王秀坤滕弘飞
崔锋哲,王秀坤,滕弘飞,2
(1.大连理工大学计算机科学与技术学院,辽宁 大连 116024;2.大连理工大学机械工程学院,辽宁 大连 116024)
双系统合作式协同进化算法求解不可分解函数
崔锋哲1,王秀坤1,滕弘飞1,2
(1.大连理工大学计算机科学与技术学院,辽宁 大连 116024;2.大连理工大学机械工程学院,辽宁 大连 116024)
针对不可分解函数求解问题,基于合作式协同进化(cooperative co-evolutionary,CC)框架,发展一种双系统协同进化算法。该算法给出一种双系统A,B的 CC框架新结构形式及其相应的协调机制,以增加算法的多样性和收敛性;给出双系统A,B各自求解的两种算法,例如差异进化、改进粒子群算法选择原则和匹配方式,使该两种算法具互补性,并且与双系统A,B各自角色相匹配,目的是提高基于CC框架双系统算法的计算性能。经不可分解函数集(维数D=1 000)测试表明,本文算法计算性能(计算精度和标准差)与其他3种典型算法相比,对于其中某些函数求解占优,总体上4种算法对函数集的求解各有所长,具有互补性。
不可分解函数优化; 合作式协同进化; 双系统框架; 现代启发式算法; 算法选择和匹配
0 引 言
不可分解函数优化问题的工程背景之一是复杂耦合工程系统优化和控制问题,该问题研究有助于揭示复杂耦合系统问题的本质,开拓求解思路、方法及其应用,这是一个重要而又难解问题。单纯用现代启发式算法(进化算法和群智能算法)求解困难。近年来,用文献[1]提出的合作式协同进化算法(cooperative co-evolutionary algorithm,CCEA)的协同进化 (cooperative co-evolutionary,CC)框架和其他综合算法求解该问题取得了重大进展[2-4]。
但是,对于测试函数集(Benchmark)[5-6]的各个测试函数Fi(i∈n)而言,目前还难有一种算法对每个测试函数Fi求解结果都比其他算法更好,而是各种算法对于Benchmark[5-6]中各函数Fi求解能力各有所长,也即各算法之间具有互补性。现有的算法对其中某些函数求解尚缺乏有效求解,远未达到其最优解。
本文算法的基本思想是,基于双系统CC框架,采用分而治之策略,将系统分解为若干个相对独立的子系统并行求解。给出新的双系统CC框架结构形式和协调机制[1]。该协调机制是针对双系统CC框架算法改进的协调机制,它包括双系统之间的信息交流,合作个体选择和其系统评价方式。此外,给出双系统A,B求解算法选择和匹配方式。
不可分解函数的定义[6]:设一个个体X={xd|d=1,2,3,…,D}表示D维函数问题的解,如果函数f(X)的X中任意两个变量xd是相互关联(耦合)的,则称f(X)是不可分解函数。如果其中任意一个变量是相互独立的,则称函数f(X)是可分解的函数[6]。
1994年,文献[1]对不可分解函数Rosenbrock利用合作式协同进化遗传算法(cooperative co-evolutionary genetic algorithm,CCGA)求解,函数变量的合作个体选择采用(a)最佳合作个体选择和(b)最佳与随机个体组合选择两种方式,经Benchmark[1]测试结果表明,后者计算结果较好,原因是它比最佳合作个体选择更有助于增加种群的多样性。文献[3]提出基于CC框架新的协同进化粒子群算法(novel cooperative co-evolutionary particle swarm optimization,CCPSO2)求解不可分解函数,仿真实验表明该算法比用进化算法整体优化例如基于有效利用种群策略的粒子群算法(efficiency population utilization strategy for particle swarm optimizer,EPUS-PSO)效果好。
基于CC框架算法求解不可分解函数优化问题的研究主要包括以下方面[2-4,7-9]:
(1)发展CCEA新的求解算法。重点研究基于CC框架的求解算法。2004年,文献[7]提出了基于CC框架的合作式协同粒子群算法(cooperative particle swarm optimizer,CPSO),包括CPSO-SK和CPSO-HK。经Benchmark[7](维数D=30)测试结果表明,CPSO求解不可分解函数F1,F4的性能要优于传统的粒子群算法(particle swarm optimization,PSO)。2011年,文献[10]将协同搜索策略与量子行为的粒子群优化算法(quantum-behaved particle swarm optimization,QPSO)相结合,提出了具有量子行为的协同粒子群优化算法(MQPSO)。经Benchmark (D=50)测试结果表明,MQPSO_20求解不可分解函数F2的性能要优于传统的QPSO和标准粒子群算法(standard particle swarm optimization,SPSO)。
(2)基于CC框架的不可分解函数变量集合对半划分的变量分组。2005年,文献[8]提出了新的合作式协同差异进化算法(cooperative co-evolutionary differential evolution,CCDE),并提出将变量集合对半分组策略。经Benchmark[9]中的函数F1-F5(D=100)测试结果表明,CCDE相对于传统的差异进化算法(differential evolution,DE)、遗传算法(genetic algorithm,GA)和CCGA具有更好的计算性能。

2008年文献[2]提出和探索的上述动态变量分组工作对于求解高维不可分解函数是一项新的贡献,近年来后续研究也取得进展。该研究意义在于涉及复杂耦合系统的各子系统间耦合和协同效应分析,以及如何处理的核心问题。该问题一旦解决,将有深远影响。当然,即使不计计算代价,也尚有不少难关有待攻克。
接下来,介绍双系统(双种群)进化算法研究现状。
近年来有些研究学者研究了现代启发式算法的双种群算法,例如研究双种群差异进化算法(differential evolution with double population,HDEDP)[13]和双种群遗传算法(dual population genetic algorithm,DPGA)[14],该双种群算法不是基于CC框架。前者用于求解3个较简单的工程设计优化测试题(焊接梁设计,压力容器设计和耐张力绝缘串设计问题),案例验证表明该算法是有效的。后者用于求解多模态函数优化问题,采用Benchmark测试集[9](与本文的Benchmark[5-6]不同)求解的维数D=30,计算结果与其他文献相比,各有短长。
此外,文献[15]发展了一种基于CC框架双系统(双种群)进化算法,简称双簧管-CCEA (Oboe-CCEA),用于求解卫星舱组件布局优化问题。值得说明该算法是针对卫星舱组件布局优化问题,而不是针对不可分解函数求解,没有讨论不可分解函数求解问题。本文与Oboe-CCEA在双系统结构,协调机制(包括信息交流合作个体选择,及其评价),以及双系统求解算法方面有不同,在文后加以说明。目前,采用这种基于CC框架的双系统协同进化算法求解不可分解函数的讨论尚少见。
综上所述,针对不可分解函数求解问题,虽然基于CC框架算法(CCEA)研究取得进展,但是求解Benchmark中某些函数,结果距其最优解有相当大的距离。各种算法对于Benchmark中各种函数求解各有所长。本文探讨如何提高基于双系统CC框架算法求解不可分解函数问题计算性能。本文目的是发展一种双系统合作式协同进化算法,对于Benchmark中某些函数求解明显有效,与现有的经典算法具互补性,共同有效地求解尽量多的不可分解函数。本文求解变量维数D=1 000。值得说明,动态变量的分组方式研究是一项很有意义的工作,有待以后讨论。
本文重点研究如何提高基于CC框架算法或CCEA求解不可分解函数优化问题的计算性能,从以下两方面进行研究:①发展一种新的双系统CC的结构形式及相应的其协调机制;②给出CC框架双系统A,B各自求解的现代启发式算法(例如DE,PSO)的选择和匹配方法。本文着重研究如何提高求解不可分解函数问题计算性能,采用通用Benchmark[5-6]评价指标:计算精度和鲁棒性(标准差),采用通用Benchmark[5-6]测试(变量维数D=1 000)。文献[3-4,16]典型算法的评价指标不涉及计算效率或计算复杂度。
1 本文算法DCCDE/PSO
1.1本文DCCDE/PSO算法特点
针对不可分解函数,本文发展一种双系统协同进化算法(dual-system cooperative co-evolutionary differential evolution particle swarm optimization DCCDE/PSO),它是基于文献[1]提出CCEA的CC框架,与CCEA不同之处是基于双CC框架。本文基于双系统A,B的CC框架算法与Oboe-CCEA主要不同之处:
(1)双系统CC框架的结构形式不同:Oboe-CCEA对A系统没有采用CC框架,采用整体优化和粗-细变粒度策略,虽然有助于A系统的系统优化问题整体求解,但是其中某些参数需人工设置,比较麻烦,所以本文算法的 A,B系统都是基于CC框架,并行计算。本文A系统不用整体优化,所以没有采用变粒度策略。
(2)协调机制不同。①Oboe-CCEA采用最佳合作个体选择方式[17],不利于迭代前期增加算法的多样性。在迭代前期,本文采用最佳与随机个体混合的合作个体选择的协调机制[17],增加种群的多样性。在迭代后期,本文利用精英保留策略和精英解集档案(Archive)[18]策略,与Oboe-CCEA不同,A系统从该精英解集档案中选择合作个体,有助于算法的收敛性。②A,B系统之间双向信息交流。本文采用个体迁移方式,而Oboe-CCEA采用部分子个体或个体方式迁移。③完整解的评价。Oboe-CCEA采用A系统,本文用A,B系统各自评价。本文目的是提高算法计算精度。因为Oboe-CCEA是B系统基于一个CC框架,发挥B系统的子系统之间的协同效应。而本文是基于两个CC框架,不仅发挥A,B系统各自子系统之间的协同效应,而且还发挥A,B系统之间的互补效应,有助于提高算法的收敛性。因为本文算法和Oboe-CCEA分别采用两个或一个CC框架,自然前者比后者耗时多。Oboe-CCEA既没有讨论也不是针对不可分解函数求解问题,所以文后Benchmark测试没有与Oboe-CCEA对比。
(3)本文给出双系统CC框架中A,B系统各自求解算法(DE,PSO)的选择和匹配方法。Oboe-CCEA的系统A,B都采用GA,没有讨论此问题。本文算法的系统A采用多样性好、搜索能力强的DE[19]求解;系统B采用具有搜索初期搜索速度快和克服后期易早熟的较好性能的探测粒子群(detecting particle swarm optimization,DPSO)[20]求解,这两种算法互补性好,并分别与系统A,B功能(角色)相匹配。
1.2本文算法DCCDE/PSO基本框架
本文算法的双系统框架如图1所示。

图1 DCCDE/PSO框架图Fig.1 Framework of DCCDE/PSO
1.3基于CC框架的系统分解
将系统或测试函数Fi个体置于CC框架,将测试函数Fi采用横向分解方式,将它截成E个子函数表达式(视为子系统或子个体),则该函数Fi可以表示为Fi(X),其中X={xi| i∈I=1,2,…,n},Xe={xie| i∈I,e∈E=1,2,…,E} 即将X分解为E个子系统。
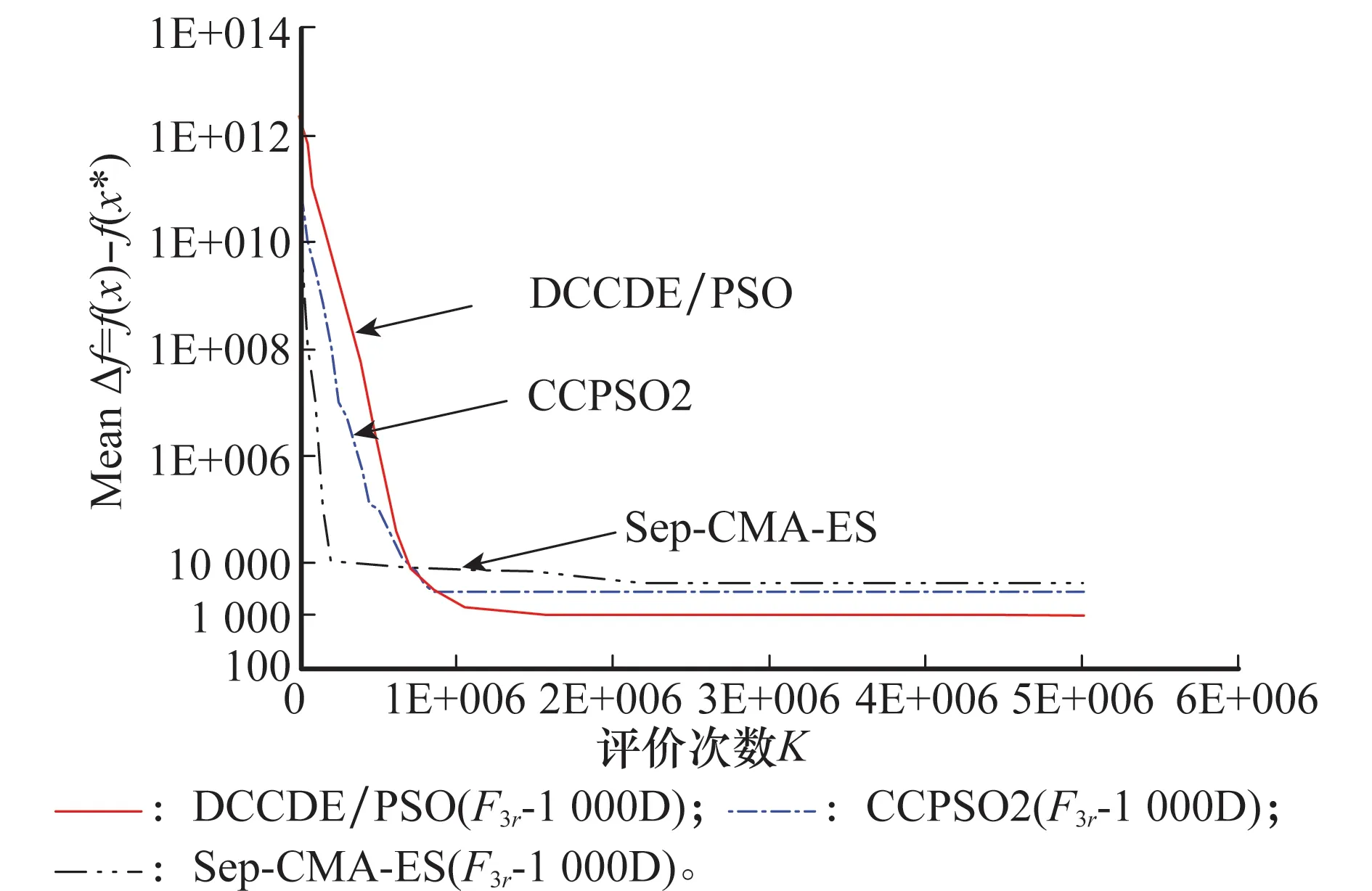
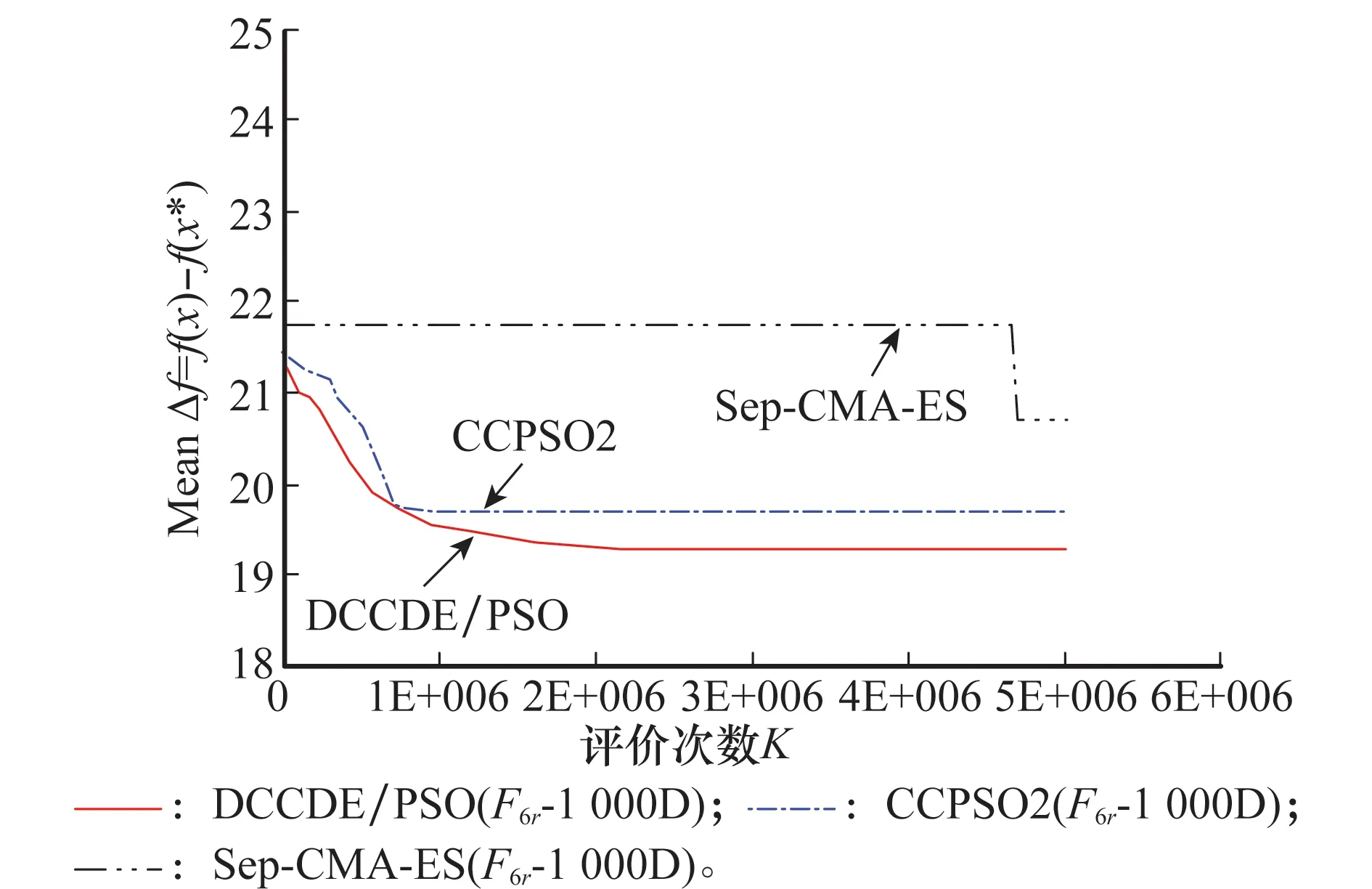
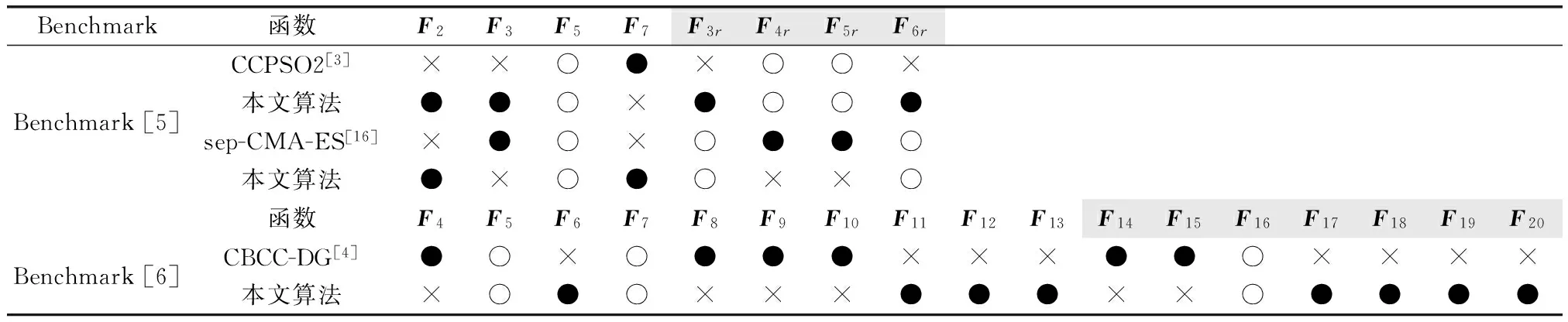
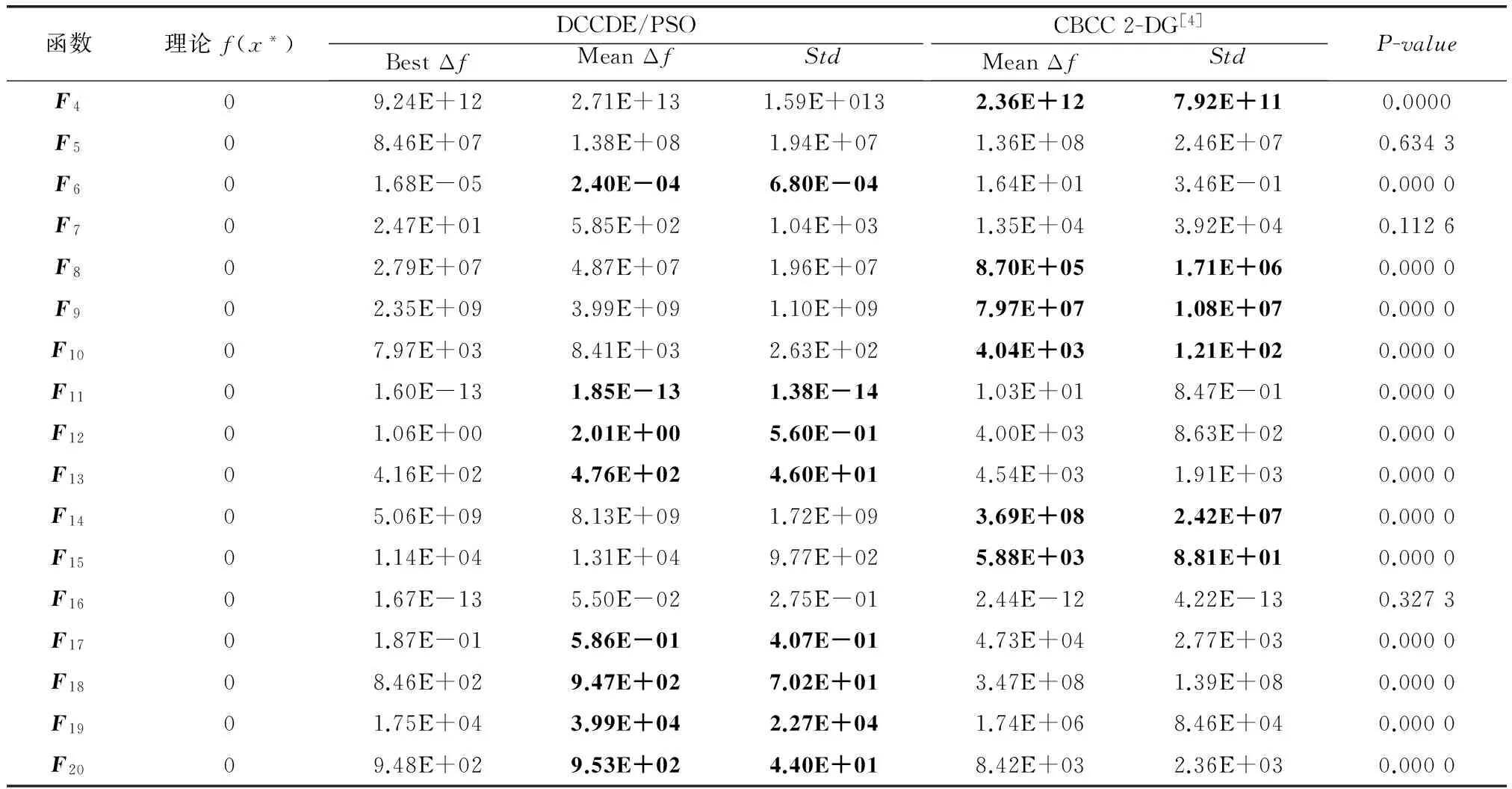
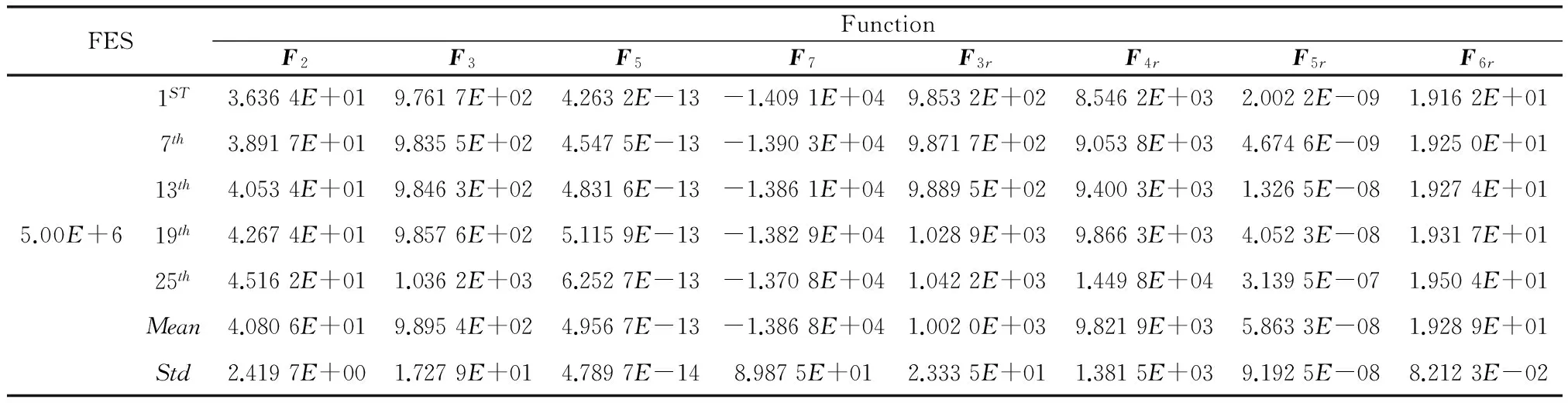
附带说明,上述Fi的分解,相当于变量集合X分组。X={Xp},分成p个相对独立的小组,p=2,3,…,P,1 1.4本文双系统DCCDE/PSO协调机制 本文双系统CC框架的协调机制是基于CCEA的隐式协调机制。CCEA的隐式整体协调机制与合作个体的选择相关,常用的合作个体选择方法有:随机选择、合作者群体选择、最优个体选择[17]以及档案(Archive)[16]方法。本文算法将A,B系统分解为E个子系统Ae,Be,e=1,2,…,E,Ae之间,Be之间,存在耦合关系,以及A,B之间,存在互补关系。需要在进化过程中保持整体协调一致性。 设本算法系统A,B各自的迭代最大评价次数为2 500×D,给出迭代前期和后期的判别式 (1) 式中,m和ε分别表示间隔代数和许用值。 为了增加算法收敛性,A,B系统还采用精英保持策略,并建立精英解集档案(Archive)[16]。该精英解集档案作用是,A系统通过该档案向B系统迁移精英个体,增加算法收敛性。在迭代后期,A系统基于CC框架的合作个体选择是从精英解集档案(Archive)中选择,组成完整解,以提高算法的收敛性。最终使B系统逼近担任主要角色的A系统,A系统逼近P系统(原问题)。本文个体迁移的时机、数量参见文献[15]。 1.5CC框架中求解的混合算法选择和匹配 本文试算经验表明,算法选择应该与双系统的A,B担任的角色相匹配。本文算法的A,B系统担任角色和关系:一是A,B系统之间既属于协同关系,又属于主辅关系;二是B为A提供优良的系统完整解(含子个体)资源;三是A系统是最终决策者;四是本文算法收敛过程使B逼近A,A逼近P(原问题)。以上是混合算法选择和匹配的依据。 本文系统A,B分别采用DE[19]和DPSO[20]算法求解,这是经过采用不同的算法组合(例如DE/PSO,DE/DE,PSO/PSO等)试验获得。DE具有全局和局部并行直接搜索、多样性好的搜索性能,适于求解高维、非线性函数问题。DPSO[20]是一种改进的PSO,它在PSO种群中选少量的子种群作为探测粒子,做收敛螺旋轨迹探索,从而实现一种普通粒子群体搜索与探测粒子个体搜索协同的搜索行为,除保持PSO的全局搜索能力好和搜索初期搜索速度快的特点而外,并较好地克服PSO算法后期收敛速度慢,局部搜索能力较弱的缺陷。此外,本文针对DPSO种群的最优位置(Globalbest,Gbest)采用Lévy变异算子,可以进一步提高克服容易早熟的能力。 综上所述,基于CC框架的系统分解,本文的双系统协调机制在迭代前期增加多样性,在迭代后期增加收敛性。系统B为系统A提供更多的全局搜索的完整解(含子个体),而系统A利用合作个体选择方式和求解算法DE的多样性和收敛性兼优的特点实现进一步优化。在迭代后期,利用精英解集档案的合作个体选择构成A系统的精英个体,A系统向B系统输送精英个体。通过双系统之间个体相互迁移,不断进化。算法DE和DPSO二者在迭代过程发挥各自所长和互补性,并与A,B系统承担角色相匹配。本文算法不仅发挥双系统A,B的各自子系统的协同效应(有别于Oboe-CCEA主要发挥B系统子系统的协同效应),而且更好地发挥系统A,B之间的协同效应,目的是提高其计算能力。最终使系统B逼近系统A,系统A逼近原系统P。 1.6基于CC框架的系统分解和变量分组 CCEA基于CC框架的系统分解如第1.3节所述。将Benchmark中测试函数Fi的个体分解为若干个子个体,也即相当于从系统角度实现变量分组。变量分组分两种:一种是静态(固定)变量分组,分组后不再改变;另一种是动态(可变)变量分组[2]。一般情况下,后者比前者有效,当然也需付出代价。本文采用前者方式,意在探讨在变量静态分组情况下,如何提高本文算法求解不可分解函数的计算性能,并借此分析不可分解函数Fi的函数性质,以及分析本文算法求解各Fi的能力好或差的原因。 1.7算法流程 DCCDE/PSO流程的伪代码如下所示。 Algorithm:Pseudocode of DCCDE/PSO 1.{Pe}←DecomposedSystem(P),P={Pe},e∈S 2.{Ae},{Be}←CopySystem(PPe),A={Ae},B={Be},e∈S//the number of AAeis not equal to the number of BBe,that is the subsystem number of system A is not equal to the subsystem number of system B. 3.Ae,Be←initPop()//Random initialize population system A and B,respectively; 4.K=1 5.While (termination criterion not met)do 6.A,B←ParallelComputation() 7.Parallel.for each subsystem Aedo 8.OneDESolve(Ae)//each subsystem AeParallel computation 9.End for 10.Parallel.for each subsystem Bedo 11.OneDPSOSolve(Be)//each subsystem BeParallel computation 12.End for 13.IfK 16.else 19.End if 20.If migration conditions is met do 27.K=K+1 28.End While 2.1测试函数 本文算法与目前典型的算法CCPSO2[3],改进的协方差矩阵自适应进化策略(smallest possible modification covariance matrix adaptation evolution strategy,sep-CMA-ES)[16]和CBCC-DG[4]这3种典型算法计算结果相比较。采用相同的Benchmark[5-6]和该Benchmark要求的评价指标:计算精度(误差平均值MeanΔf)、鲁棒性(标准差standard deviation,Std)和相同的函数变量维数(dimension,D),本文D=1 000。最大迭代次数Kmax=5 000×D。 选择文献[3,16]采用的Benchmark测试函数[5]中具代表性函数F2,F3,F5,F7,F3r,F4r,F5r,F6r,计8个不可分解函数,文献[3]中的Benchmark[5]中测试函数F3r,F4r,F5r,F6r经坐标变换,使该函数更复杂难解;文献[4]采用的Benchmark测试函数[6]中的17个不可分解函数F4-F20进行测试。两Benchmark共计25个测试函数。 下面较详细介绍不可分解函数数学定义[6]。 定义1如果函数f(x)满足式(2)的条件,则称函数f(x)是可分解的函数。 (2) 定义2如果函数f(x)任意两个变量是相互关联的,则称f(x)是不可分解函数。 有关测试函数的其他性质参见文献[5-6],其中有些测试函数性质,文后进行分析。 本文DCCDE/PSO算法设置如下: (1)每个测试函数都独立随机运行25次,试验结果取25次计算的误差平均值(计算结果与最优解的误差的平均值Mean Δf)。误差Δf=f(x)-f(x*),x*为测试函数的最优解。 (2)设置双系统A,B各自的种群规模M为25。本文采用静态变量分组,本文A系统横向分解子系统数目EA=5(即将函数Fi表达式截断后的数目),B系统横向分解子系统数目EB=2EA。A,B种群规模M数目分别与EA,EB数目对应。 (3)根据文献[19]对Benchmark[5-6]中函数多次测试推荐:取DE[19]的交叉因子CR=0.9,缩放因子F=0.5,采用的变异交叉策略为Rand1Exp;同样根据文献[20]的推荐:取DPSO[20]的惯性系数W=0.9,加速度系数C1=C2=2.05,探测粒子数Ms=1,探测粒子一次螺旋路径搜索的采样点个数T=10;螺旋运动学习因子Cs1=Cs2=0.8。 (4)文献[5-6]函数最大评价迭代次数分别为Kmax=5 000×D,Kmax=3 000×D (D为变量的维数)。许用值ε=0.5,间隔代数m=1 000。 (5)本文算法数值实验运行环境为Windows7操作系统,Inter(R)I7-3770处理器,8GB内存。 2.2结果和讨论 2.2.1结果 图2~图5分别给出了本文算法、CCPSO2和sep-CMA-EM 3种算法求解坐标轴旋转的F3r,F4r,F5r,F6r(1 000维)不可分解函数误差平均值(Mean Δf)进化曲线图。 图2 F3r误差平均值(MeanΔf)收敛曲线Fig.2 Diagram of F3r Mean Δf convergence curve 图3 F4r误差平均值(MeanΔf)收敛曲线Fig.3 Diagram of F4r Mean Δf convergence curve 本文算法与目前典型的CCPSO2[3],sep-CMA-ES[16]和CBCC-DG[4]的3种算法计算性能的两评价指标为计算精度(Mean Δf)和鲁棒性(标准差Std)。采用上述经典算法的评价指标和测试方法是:先进行T检验,考虑Mean Δf和Std,计算P-Value。当P-Value≥0.05,认为两算法相当;当 P-Value<0.05,两算法不相当。这时,两种算法比较采用Mean Δf评价,愈小愈好。以下两算法之间比较,采用此方法,每种算法各25次计算。同样,本文算法与CCPSO2[3]或sep-CMA-ES[16]通过Benchmark[5](包含8个不可分解函数)测试比较,以及本文算法与CBCC-DG[4]通过Benchmark[6](包含17个不可分解函数)测试比较,结果见表1。 图4 F5r误差平均值(MeanΔf)收敛曲线图Fig.4 Diagram of F5r Mean Δf convergence curve 图5 F6r误差平均值(Mean Δf)收敛曲线图Fig.5 Diagram of F6r Mean Δf convergence curve Benchmark函数F2F3F5F7F3rF4rF5rF6rBenchmark[5]CCPSO2[3]××○●×○○×本文算法●●○×●○○●sep-CMA-ES[16]×●○×○●●○本文算法●×○●○××○函数F4F5F6F7F8F9F10F11F12F13F14F15F16F17F18F19F20Benchmark[6]CBCC-DG[4]●○×○●●●×××●●○××××本文算法×○●○×××●●●××○●●●● 注:1)●表示占优,○表示相当,×表示较差; 2)阴影背景函数表示难解函数。 表2~表4分别给出本文算法与CCPSO2[4],sep-CMA-ES[16]和 CBCC-DG[4]算法计算结果数据比较。 表5给出本文算法对Benchmark[5]Fi(D=1 000)中8个不可分解函数计算结果排序,标记出用箱线图(Boxplot)中的5个统计量:1ST(Best),7th,13th(Median),19th,25th(Worst)的Δf,以及25次计算的Mean Δf和Std。用于说明本文的Mean Δf和Std来源。 上述其他两种算法基于单系统CC框架算法的迭代最大评价次数为5 000×D,由于本文算法采用双系统结构,因此本算法系统A,B各自的迭代最大评价次数为2 500×D,以示公平。 表2 本文算法DCCDE/PSO 与CCPSO2算法25次计算结果比较(D=1 000) 注:1)F7的最优解未知,期望f(x*)值越小越好,CCPSO2计算结果引自文献[3]; 2)DCCDE/PSO与CCPSO2采用双侧T检验,α=0.05,如果二者算法的统计结果有显著性差异,则最好的计算结果用黑粗体表示。 表3 本文算法DCCDE/PSO 与sep-CMA-ES 算法25次计算结果比较(D=1 000) 注:1)DCCDE/PSO与sep-CMA-ES采用双侧T检验,α=0.05,如果二者算法的统计结果有显著性差异,则最好的计算结果用黑粗体表示。 表4 本文算法DCCDE/PSO 与CBCC-DG 算法25次计算结果比较(D=1 000) 表5 本文DCCDE/PSO算法对8个不可分解函数25次计算结果(D=1 000)1) 注1):1ST表示最优计算结果(Best),13th表示中位数(Median),25th表示最差计算结果(Worst)。 2.2.2讨论 本文算法与CCPSO2[3],sep-CMA-ES[16],CBCC-DG[4]3种典型算法计算结果见表1~表5,以下对其进行比较和讨论。 (1)不可分解函数F3r-F6r迭代的MeanΔf收敛曲线的讨论 按T检验和单评价指标MeanΔf评价Benchmark计算结果,由图2~图4可见,当D=1 000时,对于F3r,F6r收敛曲线,本文算法(DCCDE/PSO)与CCPSO2收敛速度相当,而本文算法MeanΔf值最小。对于F4r收敛曲线,与CCPSO2相比,本文算法收敛速度较慢。对于F5r收敛曲线,本文算法在迭代前期趋向收敛较慢,但是在迭代后期下降幅度较大,本文算法MeanΔf值最小,体现了本文算法潜在的较强的计算性能,在图4中体现尤为明显。这主要归因于本文算法采用的双系统框架,相应的协调机制,以及双系统之间的协同效应。本文算法与sep-CMA-ES相比,后者收敛或停滞都较快,例如对F4r,F5r收敛非常快,而对F3,F6r停滞特别快。sep-CMA-ES收敛或停滞比较快的原因是,它利用协方差矩阵的主元分析,构造与前一代搜索方向共轭的新的演化路径,它的协方差矩阵是对角阵,有利于引导着种群变异方向引导,当然计算也较复杂。 (2)本文与其他3种算法计算结果讨论 本文算法与CCPSO2[3],sep-CMA-ES[16]和CBCC-DG[4]3种算法计算结果比较见表1。采用T检验和单评价指标MeanΔf评价。 本文对Benchmark[5]和Benchmark[6]中25个函数Fi进行测试,采用如下方法。 当算法的P-value≥0.05,两算法相当。对于表2函数(F5,F4r,F5r),P-value≥0.05,认为本文算法与CCPSO2相当。对于表3函数(F5,F3r,F6r),同理,本文算法与sep-CMA-ES相当。对于表4函数(F5,F7,F16),同理,本文算法与CBCC-DG相当。 当算法的P-value<0.05,只考虑MeanΔf值,MeanΔf愈小愈好。 1)本文算法与CCPSO2[3]相比,按照MeanΔf指标进行比较,在Benchmark[5]8个函数中,①本文算法占优的有4个函数,其中对于F3,本文算法的MeanΔf比CCPSO2高1个数量级,Std小1个数量级;②相当的有3个函数。③本文算法不如CCPSO2的函数有1个,如表1所示。 2)本文算法与sep-CMA-ES[16]相比,按照MeanΔf指标进行比较,本文算法求解的8个不可分解函数[5]中:①本文算法占优的有2个函数;②相当的有3个函数F5,F3r,F6r;③本文算法不如sep-CMA-ES函数有3个,见表1。 3)本文算法与CBCC-DG[4]相比,按照MeanΔf指标进行比较,在Benchmark[6]17个不可分解函数中:①本文算法占优的有8个函数;②相当规则函数有3个函数;③本文算法不如CBCC-DG函数有6个函数,如表1所示。 本文算法的MeanΔf和Std两项都优于CBCC-DG的8个函数,其中5个函数(F6,F11,F13,F18,F20)为多峰不可分解函数,其余3个为单峰不可分解函数。对于F11,,本文算法的MeanΔf比CBCC-DG的高14个数量级,Std小15个数量级。对于F18,本文算法的MeanΔf比CBCC-DG高6个数量级,Std小7个数量级。 (3)算法比较结果分析 首先分析本文算法对于某些函数表现差的原因如下: 1)CCPSO2对于F7优于本文算法的原因是,F7是最优解未知,内含有双重随机干扰,函数面崎岖不平,属于多峰的不可分解函数。CCPSO2计算结果表明,虽然CCPOS2是基于一个CC框架,但是在优化的前期和后期,采用动态随机调整变量(动态)分组方式(这比本文的静态分组效果较好),并采用基于柯西-高斯相结合的变异算子更新粒子的邻接位置(Lbest),以及采用环形的结构定义局部邻域,增加了算法的空间探索能力,适用于求解多峰函数F7。本文算法不具有该针对性搜索性能。 2)sep-CMA-ES对于F4r,F5r优于本文算法原因是,该算法采用子代种群规模变化和自适应的变异两种策略。对于F5r,属于多峰、坐标轴旋转的不可分解函数,该函数对于算法子代种群规模增加不敏感,所以该算法采用自适应的变异策略,通过比较当代与父代的均值之间的关系,更新协方差矩阵来实现个体变异方向,这种个体变异方向增加了算法的探索能力。对于F4r,属于多峰、坐标轴旋转函数。sep-CMA-ES改变求解策略,改采用不断扩大子代种群规模,才能在个体均值邻域周围更加有效的采集样本,以获得较好的计算结果。本文算法不具有该算法这种针对性的搜索性能。但是sep-CMA-ES算法采用上述何种策略,需要算法对种群规模变化敏感性进行试算,需要付出相应的计算代价。 3)CBCC-DG在17个不可分解测试函数中,有6个函数F4,F8,F9,F10,F14,F15优于本文算法,其中F14,F15为完全不可分解函数,前者为单峰,后者为多峰,其余的4个为非完全不可分解函数。以下讨论对于F14,F15优于本文算法的原因,CBCC-DG算法采用变量自动动态分组策略,即耦合变量差分分组策略。该策略包含分组结构的识别和优化两个部分,分组结构的识别是按照文献[4]中定理1:按顺序比较第一个变量和其余变量的关联关系,依次循环迭代,直到检测所有变量与第一个变量的关联关系,此时第一个子种群建立完毕。如果没有探测到关联关系,那么该变量被认为或许是可分解的变量,则将它分到其他不同的组,将上述探测过程循环迭代,直到探测到所有变量之间的关联关系。但是实现这种两两变量组合识别方式相当耗时。CBCC-DG以此量化每个子种群对于测试函数适应度函数值的贡献并依次分配计算资源。另外,按上述耦合变量差异进行变量分组策略,对F14和F15以及其余4个函数进行变量分组,力求使测试函数的各变量分组相对独立,有助于优化,提高计算精度。本文没有采用这种动态变量分组策略,所以对上述6个函数不占优。本文基于CCEA的CC框架进行系统分解(静态变量分组),CC框架的系统分解的特点是,并不追求子系统之间(变量分组)严格地相对独立,而是用隐式的协调机制实现优化,缺乏从使各变量分组相对独立角度来提高其计算精度的能力。 下面分析本文算法对于某些函数表现好的原因:综上所述,采用该Benchmark常用的评价指标和方法:经T检验之后,按照MeanΔf评价指标评价。对于Benchmark[5]8个函数计算结果,与CCPSO2相比,本文占优的函数有F2,F3,F3r,F6r,4个。与sep-CMA-ES相比,本文占优的函数有F2,F7,2个。对于Benchmark[6]17个函数,与CBCC-DG相比,本文占优的函数有F6,F11,F12,F13,F17,F18,F19,F20,8个。本文算法与以上3种算法之间相当函数如前所述。 没有发现能有一种算法求解所有的Fi(i∈I)结果比其他算法都好的结果。例如文献[3]指出CCPSO2[3]与sep-CMA-ES[16]相比,在8个测试函数中,前者占优的2个,后者占优的2个,相当的4个,可见,这两种算法是互补的。 由此可见,本文算法具有一定的既可求解单峰、复杂多峰函数例如F18,F20,也可求解坐标系旋转变换的不可分解的复杂函数能力。例如本文算法对于4个坐标系旋转变换的函数中的两个函数F3r,F6r占优,F4r,F5r的求解不足。另外,由此可见本文算法、其他3种典型算法(CCPSO2[3],sep-CMA-ES[16],CBCC-DG[4])这4种算法相互之间具有互补性。 本文算法对于上述函数表现好的主要原因:一是sep-CMA-ES属于进化策略算法,不是基于CC的算法,而本文算法是基于CC框架的双系统结构。本文算法在迭代前期,采用最佳与随机混合的合作个体选择,有助于增加种群的多样性。后期基于精英解集存档合作个体选择,有助于增加算法的收敛性。二是CCPSO2和CBCC-DG是基于单系统CC框架,本文算法基于双系统CC框架,给出了新的双系统结构和相应的协调机制(包括信息交流方式,合作个体选择以及评价方式),发挥了双系统的各自的各子系统之间协同效应,以及系统A,B之间的互补效应。三是求解算法的选择和匹配,本文利用A,B系统求解的DE和DPSO各自的特点和互补性,并与A,B系统的角色相匹配。 这几种算法对于两个Benchmark[5-6]中25个不同函数(D=1 000)的求解各有短长,本文算法与其他3种算法相比,本文算法对Benchmark中某些函数计算结果占优,总体上各算法之间具有互补性。以往的研究表明,对不可分解函数Benchmark函数集[5-6]求解的各种算法计算结果的比较表明[2-5],难有一种算法对每个测试函数Fi求解比其他算法都好,一般是各有短长,这也许可借用无免费午餐观点来解释。 附带说明,关于基于CC框架与非CC框架算法之间的对比问题,本文未涉及,不过文献[3]表明,算法CCPSO2(前者)与算法EPUS-PSO(后者),用同一种PSO求解,经Benchmark[5]的测试结果表明,前者优于后者,也即表明文献[3]的基于CC系统分解CCPSO2优于整体优化求解的PSO方法。 不可分解函数优化是一个重要而又难解问题,涉及复杂耦合系统求解的本质问题,虽然Benchmark中的不可分解函数为无约束非线性函数,但是它的工程背景之一是工程耦合系统的优化与控制(一般属于带约束的非线性、非连续、多模态函数),因此研究如何提高基于CC框架算法(例如CCEA)求解高维不可分解函数能力,分析各种不可分解函数Fi及其特有函数的性质,以及探索其求解策略和应用,是有益的。这是一个引人关注而又困难的问题。为了提高CCEA算法求解不可分解函数问题计算性能,本文在前人CCEA和Oboe-CCEA,以及不可分解函数求解算法的工作基础上,针对不可分解函数的求解,发展一种基于CC框架的双系统协同进化算法(DCCDE/PSO)。 本文主要工作是: (1)发展一种新的双系统A,B的 CC框架结构,以及相应的协调机制(包括信息交流、合作个体选择及其评价)。在迭代前期采用选择随机和最佳合作个体方式组成系统完整解,有助于增加算法的多样性。为了增加算法收敛性,A,B系统还采用精英保持策略,并建立精英解集档案(Archive)。在迭代后期,从精英解集档案(Archive)中选择合作个体方式,有助于增加算法的收敛性。本文迭代前期和后期A,B之间信息交流都采用个体迁移方式实现,以及采用基于CC框架双系统A,B的各自评价方式评价。本文双系统架构不仅发挥A,B系统各自子系统之间的协同效应,而且发挥了A,B系统之间的互补效应。 (2)本文给出针对双系统CC框架的系统A,B各自求解两种算法选择和匹配方法,本文的系统A,B分别采用DE和DPSO[20]求解,发挥其各自特长和具有互补性特点,并且与系统A,B各自角色相匹配。 (3)本文算法与其他3种典型算法相比较,通过两个Benchmark[5-6]函数(D=1 000)测试结果表明,总体上几种算法对于上述两个函数测试集不同函数求解各有短长,本文算法与其他3种典型算法相比,对Benchmark中某些函数计算占优(包括难解的F3r,F6r,F17~F20),总体上各算法之间具有互补性,各算法所占贡献 (有效求解函数Fi数目)比重基本相当。 本文期望通过研究提高基于CC框架算法求解能力,并借此分析各种不可分解函数性质,以及探索其针对性求解策略,最终目的是期望提高该算法计算性能,并有助于它的工程应用。 下一步工作是:针对不可分解函数求解问题,对于基于CC框架双系统,研究合作型或竞争型协同进化算法与统计分析方法相结合方法,以便有助于它在耦合系统优化与控制方面应用。 [1] Potter M A,DeJongK A.A cooperative coevolutionary approach to function optimization[J].Lecture Notes in Computer Science,1994,866(1994):249-257. [2] Yang Z Y,Tang K,Yao X.Large scale evolutionary optimization using cooperative coevolution[J].Information Sciences,2008,178(15):2985-2999. [3] Li X D,Yao X.Cooperatively coevolving particle swarms for large scale optimization[J].IEEE Trans.on Evolutionary Computation,2012,16(2):210-224. [4] Omidvar M N,Li X D,Mei Y,et al.Cooperative co-evolution with differential grouping for large scale optimization[J].IEEE Trans.on Evolutionary Computation,2014,18(3):378-393. [5] Tang K,Yao X,Suganthan P N,et al.Benchmark functions for the CEC'2008 special session and competition on large scale global optimization[R].University of Science and Technology of China,2007. [6] Tang K,Li X D,Suganthan P N.Benchmark functions for the CEC’2010 special session and competition on large-scale global optimization[R].University of Science and Technology of China,2009. [7] Van den Bergh F,Engelbrecht A P.A cooperative approach to particle swarm optimization[J].IEEE Trans.on Evolutionary Computation,2004,8(3):225-239. [8] Shi Y J,Teng H F,Li Z Q.Cooperative co-evolutionary differential evolution for function optimization[C]//Proc.of the International Conference on Natural Computation,2005:1080-1088. [9] Yao X,Liu Y,Lin G M.Evolutionary programming made faster[J].IEEE Trans.on Evolutionary Computation,1999,3(2):82-102. [10] Zhou D,Sun J,Xu W B.Quantum-behaved particle swarm optimization algorithm with cooperative approach[J].Control and Decision,2011,26(4):582-586.(周頔,孙俊,须文波.具有量子行为的协同粒子群优化算法[J].控制与决策,2011,26(4):582-586.) [11] Sayed E,Essam D,Sarker R,et al.Decomposition-based evolutionary algorithm for large scale constrained problems[J].Information Sciences,2015,316:457-486. [12] Liu J P,Tang K.Scaling up covariance matrix adaptation evolution strategy using cooperative coevolution[C]//Proc.of the International Conference on Intelligent Data Engineering and Automated Learning,2013:350-357. [13] Huang F Z,Wang L,He Q.A hybrid differential evolution with double populations for constrained optimization[C]//Proc.of the IEEE Congress on Evolutionary Computation,2008:18-25. [14] Park T,Ryu K R.A dual-population genetic algorithm for adaptive diversity control[J].IEEE Trans.on Evolutionary Computation,2010,14(6):865-884. [15] Teng H F,Chen Y,Zeng W,et al.A dual-system variable-grain cooperative coevolutionary algorithm:satellite-module layout design[J].IEEE Trans.on Evolutionary Computation,2010,14(3):438-455. [16] Ros R,Hansen N.A simple modification in CMA-ES achieving linear time and space complexity[C]//Proc.of the International Conference on Parallel Problem Solving from Nature,2008:296-305. [17] Paul W R,Liles W C,DeJongK A.An empirical analysis of collaboration methods in cooperative coevolutionary algorithms[C]//Proc.of the Genetic and Evolutionary Computation Conference,2001:1235-1242. [18] Panait L,Luke S,Harrison J F.Archive-based cooperative coevolutionary algorithms[C]//Proc.of the 8th Annual Conference on Genetic and Evolutionary Computation,2006:345-352. [19] Das S,Suganthan P N.Differential evolution:a survey of the state-of-the-art[J].IEEE Trans.on Evolutionary Computation,2011,15(1):4-31. [20] Zhang Y N,Teng H F.Detecting particle swarm optimization[J].Concurrency and Computation:Practice and Experience,2009,21(4):449-473. Dual-system cooperative co-evolutionary algorithm for non-separable function CUI Feng-zhe1,WANG Xiu-kun1,TENG Hong-fei1,2 (1.School of Computer Science and Technology,Dalian University of Technology,Dalian 116024,China; 2.School of Mechanical Engineering,Dalian University of Technology,Dalian 116024,China) Aiming at solving the non-separable function optimization problem,a dual-system cooperative co-evolutionary differential evolution particle swarm optimization algorithm (DCCDE/PSO for short)is developed based on the dual-system cooperative co-evolutionary (CC)framework.The proposed algorithm gives a new CC framework of the dual-system A and B and its corresponding coordination mechanism for improving the diversity and convergence,and gives two algorithms for example differential evolution (DE),the improved particle swarm optimization (PSO)that it solves the systems A and B respectively,as well as complementary and matches with the roles that the systems A and B play in the dual system.The purpose is to improve computational performance of the dual system algorithm based on the CC framework.The numerical experimental results of non-separable Benchmark functions (1000-dimensional)show that the performance (computational accuracy and standard deviation)of the proposed DCCDE/PSO compared favorably against other three representative algorithms has advantages for some of functions and as a whole the four algorithms had theirselves’s strengths for the Benchmark functions and each complemented the other. non-separable function optimization; cooperative co-evolution; dual-system framework; modern heuristic algorithm; algorithm selection and match 2016-06-20; 2016-08-22;网络优先出版日期:2016-09-30。 国家自然科学基金(61472062)资助课题 TP 391.72 ADOI:10.3969/j.issn.1001-506X.2016.11.30 崔锋哲(1977-),男,博士研究生,主要研究方向为智能计算、复杂系统优化。 E-mail:Hftdlut@126.com 王秀坤(1945-),女,教授,硕士,主要研究方向为决策支持系统、数据库系统。 E-mail:jsjwxk@dlut.edu.cn 滕弘飞(1936-),男,教授,主要研究方向为产品数字化设计与制造、智能计算、复杂系统建模和优化。 E-mail:tenghf@dlut.edu.cn 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160930.1313.032.html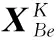

2 数值仿真实验




3 结论与展望
