基于人工噪声多用户MIMO系统的窃密算法
2016-11-11达新宇褚振勇
王 舒,达新宇,褚振勇
(空军工程大学信息与导航学院,陕西 西安 710077)
基于人工噪声多用户MIMO系统的窃密算法
王舒,达新宇,褚振勇
(空军工程大学信息与导航学院,陕西 西安 710077)
人工噪声是一种保障无线通信系统物理层安全的有效策略。现有针对基于人工噪声保密系统的窃密算法仅适用于单用户多输入单输出系统,该文针对这一问题,提出了两种适用于多用户多输入多输出(multi-input multi-output,MIMO)系统的窃密算法。首先通过基于人工噪声的多用户MIMO系统模型与盲源分离线性混合模型的比对,提出了基于盲源分离理论的窃密思路,其次通过改进两种盲源分离算法中的分离矩阵以及选择的非线性函数结构,消除了原始算法估计秘密源信号出现的相位模糊性,同时对每一步迭代中的分离矩阵进行归一化,避免了幅度的不确定性。仿真结果表明,所提两种方法在有效窃密的同时具有较低的计算复杂度,另外,当窃听天线数目越多时,窃密效果越好。
物理层安全; 多用户多输入多输出; 人工噪声; 盲源分离
0 引 言
由于无线信道的开放性和电磁信号传播的广播特性使无线通信系统对保密性以及安全性的需求变得日益突出。依赖密钥体制的传统保密系统在计算机的高速发展下不再绝对安全。利用无线信道的广播特性以及动态特征的物理层安全技术成为近年来的研究热点[1-2]。文献[3]提出保密容量(secrecy capacity)的概念并用来衡量系统的保密性能。文献[4]指出,在高斯广播信道下,当主信道容量大于窃听信道容量时,即保密容量大于零时,定义系统为安全的。然而实际中,窃听者的信道状态一般未知,无法保证其信道容量低于合法用户。为解决这一问题,文献[5]提出一种人工噪声辅助方法来保障系统的保密性。但同时文献[5]也指出当窃听者的天线数不小于发送天线时,这种人工辅助方法将会失效。在这种条件下,针对人工噪声辅助的单用户多输入单输出(multi-input single-output,MISO)系统且合法用户信道状态未知时,文献[6]提出了MUSIC-like 窃密算法,该算法利用信号子空间与噪声子空间正交的特性,对有限字符集内所有可能出现的信号序列进行遍历搜索,实现信息的获取。文献[7]提出了超平面聚类(hyperplane clustering,HC)窃密算法,该算法指出加扰信号存在超平面分布特征,并据此设计了超平面聚类算法,完成信息截获。针对基于人工噪声的单用户多输入多输出(multi-input multi-output,MIMO)系统,在已知合法用户信道状态的情况下,文献[8]提出了一种窃密算法。但是,现有文献的窃密方案均仅适用于单用户系统。在多用户场景下,信号空间特征发生改变。因而上述方法将不再可行。
针对这一问题,本文提出一种在合法用户信道状态未知的情况下适用于人工噪声辅助的多用户MIMO系统的窃密算法。首先,建立了人工噪声辅助的多用户MIMO系统模型,随后通过对窃听端信号模型的分析,将其归纳为盲源分离问题,并详细阐述了两种经典的解决盲源分离的算法,即可变步长自然梯度算法和等变自适应分解(EASI)算法,但由于窃听信号多为复信号,这两种算法在估计秘密源信号时会带来相位的模糊性以及幅度的不确定性,不能直接应用于窃密,因此本文对算法中的分离矩阵以及选择的非线性函数结构做出了限制,提出了改进的可变步长自然梯度算法和EASI算法。分析与仿真表明,这两种算法可有效窃取秘密信息,同时具有较低的计算复杂度。
1 系统模型
1.1基于人工噪声的多用户MIMO信号模型
考虑一个多用户MIMO系统,其中发送端天线数为Nt,同时向K 个合法用户发送不同的秘密信息。每个合法用户的天线数为Nr,一个天线数为Ne的窃听用户希望截获所有的K个秘密信息。所有合法用户和窃听用户已知自己的信道状态。发送端已知所有合法用户的信道状态但不知道窃听用户的信道状态。为混淆窃听用户,发送端在发送秘密信号的同时加入人工噪声干扰,因此发送信号的表达式可写为
(1)
式中,sk为发送至合法用户 k的保密信息比特符号,且Ex{SSH}=I;wk∈CNt×1是sk的发送波束成形向量;s′ 为发送的人工噪声干扰向量。
发送端到合法用户 k的信道用Nt×Nr维的hk表示,发送端到窃听者的信道用 Nt×Ne维的G表示,在多用户场景下,合法用户 k 与窃听者的接收信号分别表示为
(2)
和
(3)

为消除多用户之间产生的共道干扰 (co-channel interference,CCI),可以利用块对角化预编码(block diagonalization,BD)[9]设计波束成形矩阵W=[w1,w2,…,wK]。对于任一合法用户k(k=1,2,…,K)其波束成形矩阵应与其他所有合法用户的信道矩阵相互正交,即
(4)
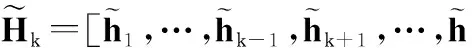
(5)
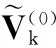
(6)
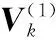
(7)
式中,Λ为对角矩阵,本文中假设其所有对角元素都为1。于是式(7)简化为
(8)
为保证人工噪声不对所有合法用户造成干扰,人工噪声必须在联合信道矩阵H=[h1,h2,…,hK],的零空间内产生,同样采用SVD分解得到H零空间的一组正交基Z∈CNt×(Nt-K),于是有s′=Zt,其中t为服从CN(0,1)分布的高斯白噪声。为保证Z的存在,本文假设K 综上,式 (1)可以表示为 (9) 将式(9)分别代入式(2)和式(3),合法用户k与窃听者的接收信号的表达式分别为 (10) 和 ye=GHWs+GHZt+ne (11) 可以看出合法用户k可以利用最大似然法解调期望信号sk,即 (12) 式中,U={u1,u2,…,um}是总数为m的符号集。但是对于窃听者而言,很难从受人工噪声干扰的接收信号中恢复出秘密信号。 1.2盲源分离的线性混合模型 假设从m个天线接收到的观测信号为x=[x1,x2,…,xm],n个信号源信号为S=[S1,S2,…,Sn],A是混合系数矩阵,盲源分离的信号模型为 x=AS+N (13) 式中,N为观测噪声向量。盲源分离[10]就在未知混合矩阵A和源信号S的任何先验信息的前提下,求得一个分离矩阵B,从观测信号x中恢复源信号S。 2.1可变步长盲分离算法 观察发现,窃听端接收信号的表达式(11)与盲源分离的线性混合模型(13)形式类似。于是有 ye=GHWks+GHZt+ne=AS+ne (14) 式中,A=GH[WZ]为混合矩阵;S=[st]为发送符号矩阵。本文采用变步长的自然梯度算法对发送符号矩阵S进行盲估计。首先对观测信号ye进行白化预处理,即 (15) (16) 式中,Vs∈CNe×K和Vn∈CNe×(Ne-K)分别为特征值对角矩阵Λs=diag{λ1≥λ2≥…≥λK}和 Λn=diag{λK+1≥λK+2≥…≥λNe}的特征向量。则白化矩阵计算如下: (17) 进行了白化预处理后,信号维数由Ne降为Nt。这时容易证明的混合矩阵Q×A是一个正交矩阵,因此分离矩阵B也是一个正交矩阵。 为了得到关于源信号S的一个良好估计,引入了目标函数: (18) (19) (20) 上述传统自然梯度算法和EASI算法收敛速度过慢,为提高收敛速度,文献[12]和文献[13]提出一种变步长的自然梯度算法和EASI算法,将迭代步长ηn也自适应地进行迭代,在算法进行n+1次迭代时,设步长迭代式为 (21) (22) (23) 2.2改进的可变步长盲分离算法 上述变步长的自然梯度算法和EASI算法具有良好的收敛性和有效性。然而由于大多数通信信号都是复数形式,上述盲源分离算法在应用到通信信号分离时会造成分离后信号的相位模糊性和幅度不确定性,这会严重影响源信号的恢复。考虑到复信号可以分成独立的同向分量以及正交分量,这两个分量都是实数,就不存在分离信号相位模糊性的问题。因此,如果能分别恢复出同向与正交分量,然后在合成复信号,就可以消除相位模糊性。 下面对上述算法中的非线性函数以及分离矩阵进行修正,从而消除相位的模糊性和幅度不确定性。首先将非线性函数进行的表达式结构转变为如下分解形式: 1≤l≤m (24) (25) 式中,br(n+1)为Bn+1的实部;bi(n+1)为Bn+1的虚部。将式(24)、式(25)代入式(19),得到变步长自然梯度算法的初始分离矩阵独立的同向与正交分量: (26) (27) 同理,将式(24)、式(25)代入式(20),得到变步长EASI算法的初始分离矩阵独立的同向与正交分量: (28) (29) 注意,当迭代次数n≥1时,将上式中的迭代步长替换为式(21),得到变步长自然梯度算法的迭代分离矩阵独立的同向与正交分量: (30) (31) 同理,得到变步长EASI算法的初始分离矩阵独立的同向与正交分量: (32) (33) 同时,为了避免输出向量幅值的不确定性,对每一步迭代得到的Bn+1均做归一化处理,即 (34) 2.3基于改进可变步长盲分离的窃密算法 综上所述,基于改进自然梯度的窃密算法具体步骤如下: 步骤1按式(14)对观测信号ye进行零均值及白化预处理; 步骤2令n=0,初始化随机权矢量B0=I、η0、γ,设定最大迭代次数为m以及选择非线性函数f(yl); 步骤3按式(26)、式(27)计算分离矩阵Bn+1的同向与正交分量; 步骤4按式(25)将Bn+1的同向与正交分量合成一个复数形式,并按式(34)进行归一化; 步骤5按式(21)计算迭代步长ηn+1,令n=n+1; 步骤6按式(30)、式(31)计算分离矩阵Bn+1的同向与正交分量; 步骤7重复步骤4~步骤6,计算所有采样时刻的分离矩阵Bn+1,直到n达到最大迭代次数; 下面通过仿真实验验证本文方法的有效性。假设H与G为瑞利块衰落信道。在下列两种场景下仿真:①发射天线Nt=4共3个合法接收用户,每个用户有Nr=2个天线;②发射天线Nt=7共4个合法接收用户,每个用户有Nr=2个天线。所有用户都采用BPSK 调制。每个天线上的噪声都是独立的高斯白噪声。本文中信噪比(signal-to-noise ratio,SNR)与信干比(signal-to-interference ratio,SIR)分别定义为信号与噪声的功率比值以及信号与人工噪声的功率比值。仿真时步长初始值均为η0=0.08,γ=0.001,非线性函数f(y)=y3+2y。为方便描述,在下文中,将改进后可变长自然梯度算法称为改进算法1,将改进后可变长EASI算法称为改进算法2。 图1 算法收敛性比较(SIR=0 dB)Fig.1 Algorithm convergence comparison (SIR=0 dB) 下面分析盲分离算法的盲估计性能,仿真中,算法1的迭代次数为400,算法2的迭代次数为200,接收信号样本个数为300个。图1为窃听用户的平均误码率与信噪比的关系曲线图。由图中可以看出:①相较于可变步长算法1和算法2,改进算法1与改进算法2 都能获得较低的误码率,其中改进算法2在较高信噪比下具有更好的窃密效果;说明本文改进后的算法可以有效消除相位的模糊性以及幅度的不确定性;②窃听天线数Ne>Nt比Ne=Nt时可误码率有很大提高,说明窃听天线数目越多,误码率越低,窃听效果越好;③合法用户总数对窃听效果的影响较小,这是因为盲分离算法对源信号的总数并不敏感 。 然后分析人工噪声功率对算法的影响,如图3 所示,随着SIR的增加,改进后算法的平均误码率逐渐降低,改进后算法2相较于改进后算法1对人工噪声的抑制性能更好,说明改进后算法1、算法2均具有良好的鲁棒性,同时也说明如果分配给人工噪声较高的功率,更有利于防止窃听。 图2 算法的误码率随信噪比变化曲线(SIR=0 dB)Fig.2 BER performance as SNR increases (SIR=0 dB) 图3 算法的误码率随信干比变化曲线(SNR=15 dB)Fig.3 BER performance as SIR increases (SNR=15 dB) 最后分析对可变步长算法1、算法2和改进后算法1、算法2进行100次盲估计实验。 通过比较平均运行时间来判断四种方法的运算复杂度。运行时间如表1所示,由表 1 可以看出,改进的算法1、算法2的运行时间与可变步长算法1、算法2几乎一样,这是因为由第3.2节可知,本文方法仅仅是对非线性函数以及盲分离矩阵做出了结构的限制,并没有增加算法的计算复杂度。 表1 算法运行时间比较 从基于人工噪声的保密系统的对立面出发,本文提出了两种针对基于人工噪声的多用户MIMO系统的窃密算法。首先构建了基于人工噪声的多用户MIMO的系统模型,在此基础上结合盲分离理论,利用可变步长的方法提高了自然梯度算法和EASI算法的收敛速度,然后通过对非线性函数形式的限制消除了原盲源分离算法带来的相位模糊以及幅度不确定。最后的仿真实验证明两种改进后算法均能有效窃取秘密信息,且具有较低的计算复杂度,其中改进后可变步长的EASI算法性能更好。窃听天线数目越多,窃听效果也越好。 [1] Chen X,Yin R.Performance analysis for physical layer security in multi-antenna downlink networks with limited CSI feedback[J].IEEE Wireless Communations Letters,2013,2(5):503-506. [2] Li N,Tao X,Xu J.Artificial noise assisted communication in the multiuser downlink:optimal power allocation[J].IEEE Wireless Communations Letters,2015,19(2):295-298. [3] Wyner A D.The wire-tap channel[J].Bell System Technical Journal,1975,54(8):1355-1387. [4] Csiszár I,Körner J.Broadcast channels with confidential messages[J].IEEE Trans.on Information Theory,1978,24(3):339-348. [5] Goel S,Negi R.Guaranteeing secrecy using artificial noise[J].IEEE Trans.on Wireless Communications,2008,7(6):2180-2189. [6] Wu F L,Wang W J,Wang H W,et al.A unified mathematical model for spatial scrambling based secure wireless communication and its wiretap method[J].Science China:Information Science,2012,42(4):493-492. [7] Lu L,Jin L,Huang K.Eavesdropping against artificial noise:hyperplane clustering[C]//Proc.of the IEEE International Conference on Information Science and Technology,2013:1571-1575. [8] Liu S,Hong Y,Viterbo E.Artificial noise revisited:when eve has more antennas than alice[C]//Proc.of the IEEE International Conference on Signal Process Communication,2014:1-5. [9] Spencer Q H,Swindlehurst A L,Haardt M.Zero forcing methods for downlink spatial multiplexing in multiuser MIMO channels[J].IEEE Trans.on Signal Procesing,2004,52(2):461-471. [10] Pham D T,Cardoso J.Blind separation of instantaneous mixtures of nonstationary sources[J].IEEE Trans.on Signal Procesing,2001,49(9):1837-1848. [11] Hyakin S.Unsupervised adaptive filtering,volume l:blind source separation[M].2nd ed.New York:Wiley,2000. [12] Fu W H,Yang X N.Novel algorithm for step-size adaptive blind source separation based on natural gradient[J].Journal of Huazhong University of Science and Technology(Nature Science Edition),2007,35(10):18-20.(付卫红,杨小牛.改进的基于步长自适应的自然梯度盲源分离算法[J].华中科技大学学报(自然科学版),2007,35(10):18-20.) [13] Fu W H,Yang X N,Liu N A,et al.Step-size optimization based EASI algorithm for blind source separation[J].Journal of Sichuan University(Engineering Science Edition),2008,40(1):118-121.(付卫红,杨小牛,刘乃安,等.基于步长最优化的EASI盲源分离算法[J].四川大学学报(工程科学版),2008,40(1):118-121.) Wiretapping strategies for artificial noise assisted communication in MU-MIMO system WANG Shu,DA Xin-yu,CHU Zhen-yong (School of Information and and Navigation,Air Force Engineering University,Xi’an 710077,China) The artificial noise (AN)-assisted strategy is invalid to guarantee physical layer security of wireless comunication.The opposite of AN-assisted strategy is investigated only for the single user case.Aiming at this,two wiretapping methods are proposed for AN-assisted multiuser multiple-input-multiple-output (MU-MIMO)system.Firstly,the idea of wiretapping based on blind source separation (BSS)is expounded by the contrast analysis of the AN-assisted MU-MIMO system model and the BSS linear structure.Then,two novel wiretapping algorithms are put forward.The permutation indetermination of secret message is removed through setting limits on the separation matrix and nonlinear function structure,and the phase ambiguity is reduced by the separation matrix normalization.Simulation results show that both of our proposed methods can intercept information effectively with a low computational complexity.In addition,the more antennas eavesdropper equipped the better average BER. physical layer security; multiuser MIMO; artificial noise(AN); blind source separation (BSS) 2016-02-26; 2016-05-26;网络优先出版日期:2016-08-16。 国家自然科学基金(61271250, 61571460)资助课题 TN 918 ADOI:10.3969/j.issn.1001-506X.2016.11.28 王舒(1987-),女,博士研究生,主要研究方向为物理层安全和通信信号处理。 E-mail:xss_wang@163.com 达新宇(1961-),男,教授,博士,主要研究方向为通信信号处理。 E-mail:dxy2008@163.com 褚振勇(1972-),男,副教授,博士,主要研究方向为通信信号处理。 E-mail:zane_chu@163.com 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160816.1504.004.html2 基于改进可变步长盲分离算法的窃密算法
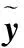
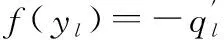
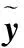
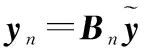

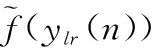
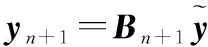
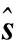
3 仿真实验
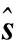
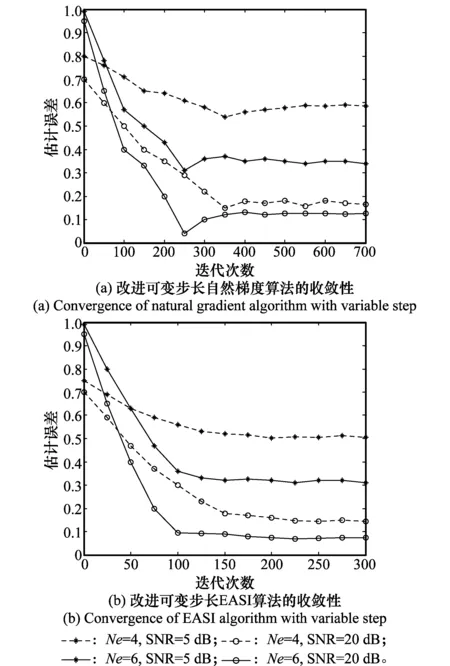
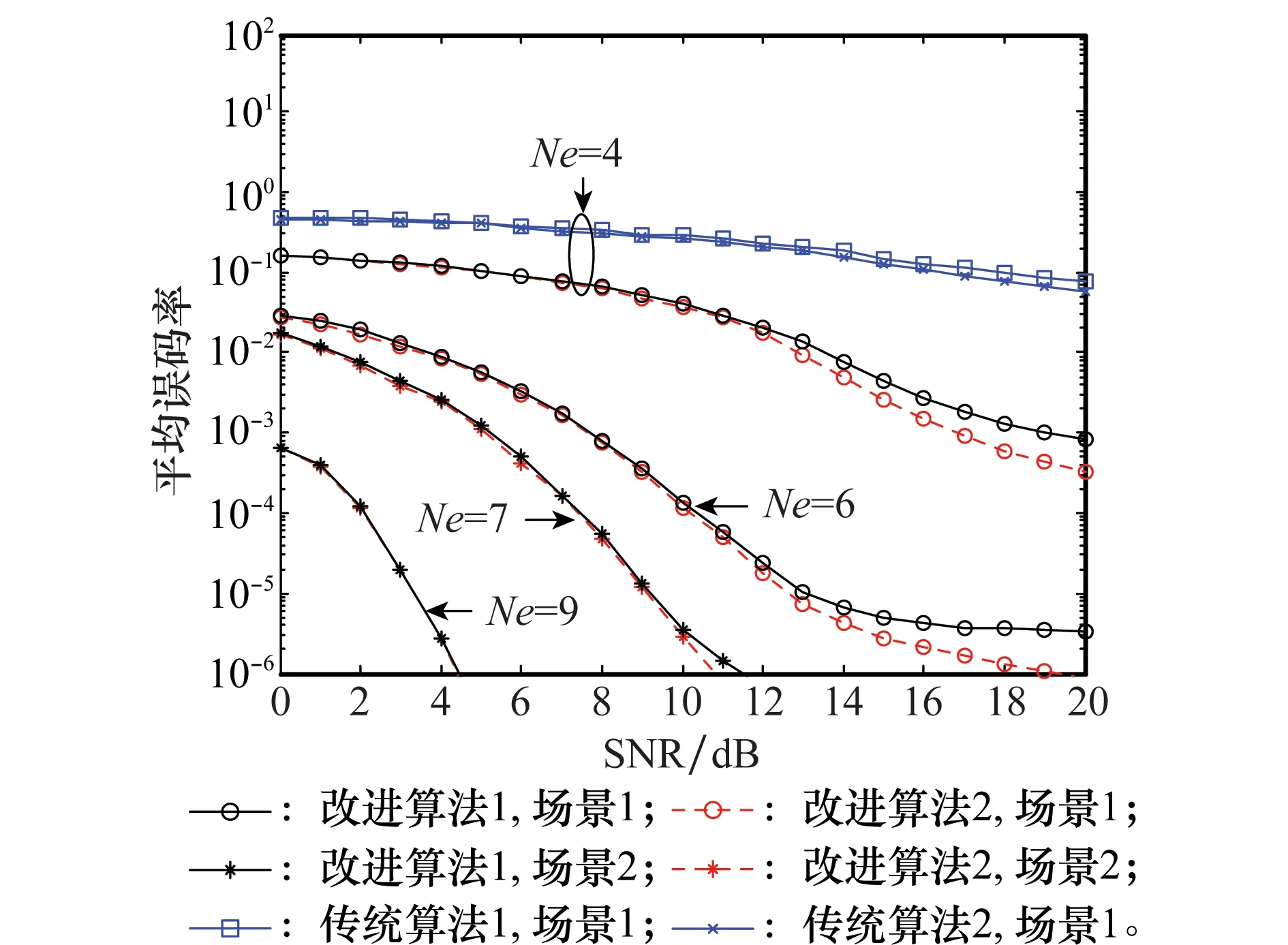


4 结束语
