可验证的安全内积计算协议的设计与实现*
2016-11-11张文科杨浩淼
冉 鹏,张文科,杨浩淼
(1.电子科技大学计算机科学与工程学院,四川 成都 611731;2.中电集团30所保密通信重点实验室,四川 成都 610041)
可验证的安全内积计算协议的设计与实现*
冉 鹏1,2,张文科2,杨浩淼1,2
(1.电子科技大学计算机科学与工程学院,四川 成都 611731;2.中电集团30所保密通信重点实验室,四川 成都 610041)
安全多方计算旨在解决一组互不信任的参与方之间隐私保护的协同计算问题。自姚期智从1982年提出以来,随着云计算、电子商务技术的发展,安全多方计算得到了更加广泛的研究及应用。余弦相似性是用于度量两个样本点之间相似度的有效方法,且广泛应用于数据挖掘、神经网络和机器学习等领域。目前存在的大多数安全多方计算研究都忽略了用户输入和结果的验证过程,都假设各参与方是诚实地执行协议。为了弥补这一块的缺陷,设计了一种可验证的安全内积计算的协议,并证实了此协议会更加安全。
安全内积计算;余弦相似性;隐私保护;可验证
余弦相似性(Cosine Similarity,CS)[4]是用于度量两个样本点之间相似度的有效方法,且广泛应用于数据挖掘、神经网络和机器学习等领域。特别是近几年,随着大数据分析的兴起,在大规模数据集中进行数据挖掘得到可使用的信息变得异常重要。余弦相似性是一个非常有用的算法,只要涉及计算两个样本点之间的相似度都可以使用它。比如,当需要查找某本书籍中的某几个关键字时,移动社交网络中查找潜在的用户或好友时,余弦相似性度量就是一个非常高效的方法。
在如今的大数据环境下,基于余弦相似性的安全多方计算协议,能够保证用户的输入信息不被泄露的情况下,通过协同计算各自输入样本点之间的相似度可以对各自的数据集进行挖掘。现有的大多数多方安全计算协议都着力于保护数据隐私,却忽略了计算的可验证性,而协议的正确性依赖于所有参与方完全诚实地遵守协议的执行。但是,在实际中很难实现。由于缺乏对参与方输入数据与输出结果的验证,恶意用户可以通过对输入数据、中间计算结果和输出结果进行撒谎,使协议得到错误的计算结果,从而破坏计算机的系统安全。对此,本文在总结前人的基础上,设计了一个可验证的安全多方计算协议,以弥补大多数安全多方计算缺乏验证过程的缺陷。实验证明,可验证的安全多方计算协议较之前的大多数安全多方计算协议更加安全。
1 相关研究
姚期智(A.C.Yao)最早于1982在著名的“百万富翁”问题[5]中提出了安全多方计算问题。百万富翁问题即有两个百万富翁,他们想在不泄露各自钱财的情况下,知道谁拥有更多的财富,实际上是比较两个整数大小的安全多方计算问题。随后,在1986年,Goldreich、Micali、Wigderson提出了可以计算任意函数的、基于密码学安全模型的安全多方计算协议[6]。该协议证明了被动攻击时n-secure的协议是存在的,主动攻击时(n-1)-secure的协议是存在的。接下来的两年,Chaum和Goldreich分别考虑了信息论安全模型和密码学安全模型下的安全多方计算问题[7]。此后,许多学者在如何提高安全多方计算协议的效率、如何对安全多方计算进行形式化的定义、如何对通用的安全多方计算协议进行剪裁使之更加有效地适用于不同的应用环境、新的安全多方计算协议的构造方法、安全多方计算攻击者结构定义等方面进行了大量研究。
虽然安全多方计算在理论上的研究很成熟,但是通用的安全多方计算协议的计算代价极其昂贵。这些现存的方法都集中考虑了隐私保护方面,却忽略了各参与方的输入和最后结果的验证过程[8]。大多数协议的正确性都是基于这样的假设:假设各个参与方都能严格执行协议。实际上,很难保证各个参与方都是完全诚实的。因此,可验证的安全内积计算协议应运而生。本文将在分析前人的结果上,设计一种可验证的安全内积计算协议。
2 基础知识
2.1 可验证的安全多方计算
可验证的安全多方计算(Verifiable Secure Multiparty Computation)问题,就是说在分布式网络中,有n个参与方,每一方都有一个自己的秘密输入,他们希望不泄露彼此的秘密输入的情况下,能够协同完成某种计算任务。要求计算结束后,他们每一方都能接收到正确的输出,且每一方只能了解自己的秘密输入和输出。这里,如果在该协议中,一个恶意参与方无法欺骗其他参与方接受一个错误的计算结果,那么就称这类安全多方计算协议是可验证的。
2.2 余弦相似性
余弦相似性是度量两个样本点之间相似度的有效方法,主要度量他们之间的余弦角θ(θ∈(0,π)),而余弦角的大小决定了两个向量之间的相似度。比如,当余弦角为0°时,说明两向量方向相同、线段重合;如果角度为90°,说明两向量形成直角,方向完全不相似;如果角度为180°,说明两向量方向刚好相反。因此,可以通过计算余弦角的大小来判断两向量的相似程度。夹角越小,说明两向量越相似。

余弦值的范围在[-1,1]之间,余弦值越接近于1,代表两个向量的方向越接近于0,他们的方向更加一致,相应的相似度也越高。
在大数据分析中,余弦相似性已经成为数据挖掘和机器学习等领域的一个重要模块。
2.3 同态加密
1978年,在RSA密码算法刚提出不久,Rivest等人提出了全同态加密算法的概念[9]。一个加密方案E如果满足对密文做任意操作后再解密,其结果与对明文进行相应操作结果相同,就称该加密方案是全同态加密方案。形式化描述为:Decrypt是方案E的解密算法,sk的私钥,pk是公钥,f(x1,x2,…,xt)是一个t元函数,则Decrypt( f (c1,c2,…,ct),sk)=f(m1,m2,…,mt)。目前的同态加密方案都是部分同态加密的,还没有完全的全同态加密方案出现。同态加密方案目前满足加同态和乘同态两种运算[10]。
①对于两个明文m1和m2,对其进行加密π(m1)=c1,π(m2)=c2,得到密文后,对密文进行加运算。如果满足c1+c2=π(m1)+π(m1)=π(m1+m2),即该加密算法满足加同态,如ElGamal加密算法。
②对于两个明文m1和m2,对其进行加密π(m1)=c1,π(m2)=c2,得到密文后,对密文进行乘运算。如果满足c1· c2=π(m1)·π(m1)=π(m1· m2),即该加密算法满足乘同态,如RSA加密算法。
本文采用快速Paillier加密算法[11]作为可验证部分的同态加密算法。
快速Paillier加密算法描述如下:
第一,选择两个素数p和q,公钥为{n, g},其中模数n=pq,本元私钥为:
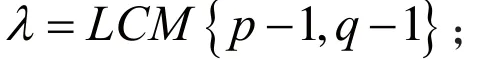
第二,加密c=E( m, r)=gm+nrmodn2;
第三,解密,即:

加法同态性:
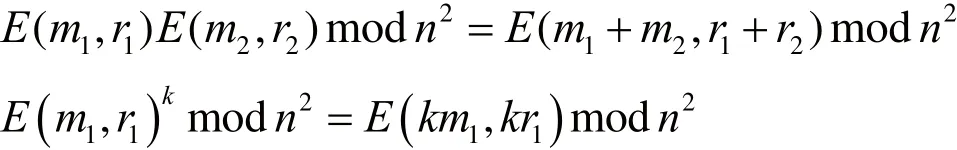
2.4 不经意传输协议
假设A有一个秘密,想以1/2的概率传递给B,即B有50%的机会收到这个秘密,另外50%的机会什么也没有收到。协议完成后,B知道自己是否收到了这个秘密,但是A却不知道B是否收到了这个秘密。这种协议称为不经意传输协议(Oblivious Transfer,OT)。
1981年,Rabin给出了最早的不经意传输协议[12]。该协议实现了“二选一”的功能,被记作协议。随后,被相继提出[13-14]。这里,只简单介绍一下协议。
3 可验证的安全内积计算协议的设计
3.1 基本方案描述

图2 基本方案
协议1描述如下:
(3)P收到Alice和Bob的秘密输入后,计算两个向量的内积以及Alice、Bob双方输入的模最后将消息广播发送给Alice和Bob;
此方法将各自的秘密输入外包到第三方,由第三方来执行计算过程,减轻了参与方的计算压力。但是,由于第三方P的存在,直接发送各参与方的秘密输入易导致输入方的隐私信息泄露,且第三方P并不是完全可信的,它不一定返回正确的内积以及模它甚至可以发送伪造或者篡改的消息给各参与方来进行欺骗。
为了保证各参与方隐私信息不被泄露,可以采用加密方案。Alice和Bob分别对各自的秘密输入进行加密运算后,再发送给可信第三方P,再由可信第三方P进行相应的运算。但是,加密操作限制了数据的使用,通信成本增加。同时,上述基本方案没有考虑参与方输入数据和输出结果的验证过程。为了安全着想,可以对第三方P的输出结果进行验证,同样P也可以对Alice和Bob的输入信息进行验证,以防篡改信息。因此,设计了可验证的安全内积计算协议。
3.2 可验证的安全内积计算协议
3.2.1 基于不可信第三方的可验证的安全两方内积计算协议(协议2)
首先简单介绍一个基于不可信第三方的可验证的安全两方内积计算协议。同样,假设有两个参与方Alice和Bob,分别拥有一个秘密向量和和以及一个不可信的第三方P(即假设P不会和Alice或者Bob进行串通)。Alice和Bob将各自的秘密输入分别外包给可信第三方P,由P来执行计算过程,然后Alice和Bob分别计算余弦相似性。同时,需要保证Alice和Bob可以对P返回的信息进行验证,以防篡改或者伪造。
协议2描述如下:
(4)不可信第三方P计算:

(5)Alice和Bob对消息m1和m2进行验证(此步骤可以单独进行,将在后文单独给出),如果验证通过,则继续协议;如果验证不通过,则终止协议;
(6)Alice和Bob通过计算:

(8)待交换过程结束后,Alice和Bob就可以分别计算余弦值。
步骤(5)中的验证过程如下:


Bob计算如下信息:

然后,Bob将e1、e2和自己的证书发送给Alice;
④同理,Alice和Bob互换角色再次执行上述步骤①到③,Bob可对Alice的输入进行验证。
下面进行安全性分析。
第一,步骤(2)和步骤(3)中,添加随机向量的目的是增加Alice和Bob初始输入向量的随机性,同时保护各自的隐私信息;
第二,步骤(5)中增加了Alice和Bob对彼此消息的相互验证过程,防止了Alice和Bob之间的欺骗行为;
第三,步骤(6)中增加了Alice和Bob对内积结果的验证过程,防止了不可信第三方P的欺骗行为。
此协议中由于不可信第三方的存在,在某种特定情形下并不完全安全。同时,由于存在证书交互过程,加大了通信成本。接下来,将设计一个无不可信第三方的无证书的可验证的安全多方计算协议。
3.2.2 无不可信第三方的可验证的安全两方内积计算协议(协议3)
同样,假设有两个参与方Alice和Bob,分别拥有一个秘密向量,协议结束后输出Alice和Bob的内积。
协议3描述如下:
(1)Alice和Bob共同协商两个整数p和m,使得pm足够大;
(4)对每一个j=1,2,…,m,Alice和Bob按照以下步骤进行计算:
①Alice生成一个秘密的随机数k,1≤k≤p;
③对每一个i=1,2,…,p,Bob计算:

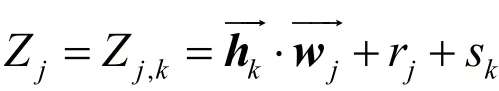
(8)Bob收到消息后,首先验证消息{u'-e}是否等于步骤6中计算得到的{u-e},如果相等,则说明Alice正确发送消息;如果不等,则终止协议。
下面进行安全性分析。
第一,在步骤(4)中,如果Bob想进行猜测攻击,那么他正确猜测的概率为由于足够pm大,因此其概率接近于0;
第二,在步骤(4)③中加入随机数rj的目的是增加Zj,i的随机性,防止了Alice猜测Bob的秘密输入向量b的行为;
第三,无不可信第三方的存在,安全性较协议2高;
第四,步骤(6)到(8)主要用于验证,由于验证过程的存在,防止了Alice和Bob彼此的欺骗行为;
第五,此协议中没有证书交互过程,通信成本较协议2更低。
4 结 语
现有的大多数安全多方计算协议没有考虑参与方输入输出结果的验证。考虑到这种情况,本文在总结前人的基础上,设计了两个可验证的安全内积计算协议,弥补了大多数安全多方计算缺乏验证过程的缺陷,大大提高了安全多方计算协议的安全性。
[1] Lu R X,Zhu H,Liu X M.Toward Efficient and Privacy-Preserving Computing in Big Data Era[J].IEEE Network,2014,28(04):46-50.
[2] Wen Liang Du.A Study of Several Specific Secure Two-party Computation Problems[D].USA:Purdue University,2000.
[3] 耿涛.安全多方计算若干问题以及应用研究[D].北京:北京邮电大学,2012. GENG Tao.Research on Several Secure Multi-party Computation Problems and Applications[D].Beijing:Beijing University Of Posts And Telecommunications,2012.
[4] De Xin Yang,ChunJing Lin,Bo Yang.A Novel Secure Cosine Similarity Computation Scheme With Malicious Adversaries[J].International Journal of Network Security & Its Applications(IJNSA),2013,5(02):171-178.
[5] YAO A.C.Protocols for Secure Computations[J].Foundations of Computer Science Annual Symposium on,1982:160-164.
[6] Goldreich O,Micali S,Wigdeson A.How to Play Any Mental Game[C].In Proceedings of the 19th Annual ACM Symposium on Theory of Computing,1987:217-229.
[7] Chaum D,Crepeau C,Damgard I.Multiparty Unconditionally Secure Protocols[C].In Proc.20th Annual Symposium on the Theory of Computing,1988:11-19.
[8] ZHANG Lan,LI Xiang-Yang,LIU Yun-hao.Verifiable Private Multi-party Computation:Ranging and Ranking[J]. In Proceedings IEEE INFOCOM,2013,12(11):605-609.
[9] Rivest R L,Adleman L,Dertouzos M L.On Data Banks and Privacy Homomorphisms[J].Foundations of Secure Computation,1978:169-179.
[10] Gentry C,Halevi S.Fully Homomorphic Encryption over the Integers[D].Palo Alto:Stanford University,2010.
[11] Paillier P.Public-key Cryptosystems based on Composite Degree Residuosity Classes[J].In Proc. of EUROCRYPT,1999,(05):223-238.
[12] Rabin M.How to Exchange Secrets with Oblivious Transfer,Technical Report TR-81,Aiken Computation Lab[D].Cambridge:Harvard University,1981.
[13] Ham L,Lin H.Noninteractive Oblivious Transfer[J]. Elcetronic Leters,1990,26(10):635-636.
[14] Naor M,Pinkas B.Oblivious Transfer and Polynomial Evaluation(Extended Abstract)[M].Atanta:ACM press,1999.

冉 鹏(1991—),男,硕士,主要研究方向为密码学理论与技术、安全多方计算;
张文科(1973—),男,硕士,高级工程师,主要研究方向为密码理论与信息安全;
杨浩淼(1974—),男,博士,副教授,主要研究方向为密码理论与技术。
Design and Implementation of Verifiable Secure Inner-Product Computation Protocols
RAN Peng1,2, ZHANG Wen-ke2, YANG Hao-miao1,2
(1.College of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu Sichuan 611731, China;2.Laboratory of Science and Technology on Communication Security, Chengdu Sichuan 610041, China)
Secure multi-party computation is designed to solve the privacy-preserving cooperative computing problem between a set of mutually untrusting participants, since A.C.Yao proposed it in 1982,with the development of cloud computing, e-commerce technology, secure multi-party computation get more extensive research and application. Cosine similarity is an effective method to measure similarity between two sample points, which is widely applied in data mining, neural network and machine learning. At present, the most existing secure multi-party computation researches ignore the verification process of user's inputs and results, all of which assume that each participant will follow the protocol honestly. So, in order to make up the blemish in this part, we design a verifiable secure inner-product computation protocol, which confirmed to be more secure.
secure inner-product computation; cosine similarity; privacy-preserving; verifiable
0 引 言
互联网的快速发展,为协同计算提供了大量机会,其结果主要依赖于各个参与方的隐私输入[1]。但是,由于互联网的开放性,直接发送各自的输入易导致隐私的泄露。因此,人们更希望能够在安全环境下进行各自协同计算,同时保护用户各自的隐私信息不被泄露,这便是安全多方计算问题。通常来讲,安全多方计算(Secure Multi-Party Computation,SMC)问题[2]是指在分布式网络环境中,一组互不信任的用户之间能够在不泄露各自私有的输入信息的情况下,协同执行某个计算任务的问题。如果存在一个可信的第三方(Trusted Third-Party,TTP),那么该类问题就可以很好地解决。我们只需要每个参与方将各自的输入分别发送给TTP,由TTP来进行计算得到最后的结果,然后再将最后计算的结果广播给各个参与方,这样每个参与方就能得到正确的结果。但是,现实生活中很难找到这样完全可信的第三方。因此,安全多方计算协议的研究应运而生。如今,安全多方计算在密码学中拥有相当重要的地位,在电子选举、电子拍卖、电子投票、秘密分享门限签名等场景中有着极其重要的作用。图1说明了安全多方计算在密码学中的地位[3]。
National Natural Science Foundation of China (No.U1633114,No.U1333127);International Science and Technology Cooperation and Exchange Program of Sichuan Province(No.2015HH0040);China Postdoctoral Science Foundation-Funded Project(No.2014M562309)
TP309
A
1002-0802(2016)-10-1369-06
10.3969/j.issn.1002-0802.2016.10.020
2016-06-16;
2016-09-12
data:2016-06-16;Revised data:2016-09-12
国家自然科学基金(No.U1633114,No.U1333127);四川省科技厅国际合作计划(No.2015HH0040);中国博士后科学基金资助项目(No.2014M562309)
