基于耦合分析的双通带滤波器设计*

宛新文，张 宇，许耀华，李民权

（安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039）

基于耦合分析的双通带滤波器设计*

宛新文，张 宇，许耀华，李民权

（安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039）

基于耦合矩阵综合的方法，辅以数值优化，可以实现不同期望目标的双通带滤波器，设计过程清晰、便捷。基于前期的分析计算，使设计后期的 仿真、优化及调试工作量明显减少。而交叉耦合的引入，能在特定频点引入传输零点，大幅提高了滤波器的性能，从而使滤波器的设计快速且准确。通过实例设计和仿真，验证了该计算方法的正确性，并对结果进行了讨论，对高性能双通带滤波器设计具有重要的参考价值。

耦合矩阵；双通带滤波器；传输零点；耦合

0　引 言

随着现代通信技术的高速发展，空间电磁环境趋于复杂，全面考验着通信系统和通信设备。微波滤波器的性能往往影响着整个通信系统的传输质量，使得对微波滤波器的要求趋于严苛［1］，更给滤波器设计带来了难度。双通带滤波器的设计方法很多，但是能实现通带预期可调节并保证通带传输特性良好的方法比较有限。本文通过计算滤波器中各谐振器间的耦合系数，得到耦合矩阵，并利用耦合矩阵构建实际电路模型，以根据预期设计目标，计算设计过程中所需的参数，从而得出较为理想的结果［2］。此外，提出在设计过程中辅以编程计算优化方法，以进一步优化目标滤波器的性能。

1　滤波器耦合分析

对于一个没有损耗的无源滤波器网络，在归一化频域s=jΩ中，其传输函数或逼近函数可以表示为［3］：

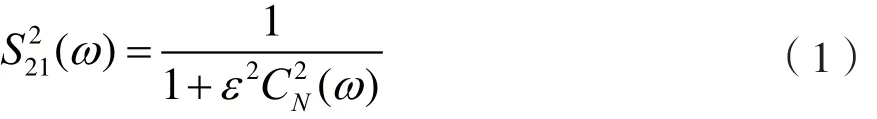
其中CN（ω）为特征函数。切比雪夫低通原型的边沿特性最接近于理想情况，所以本文选取广义切比雪夫函数分析滤波器的耦合特性，其表达式如下：

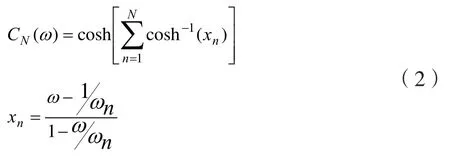
理想滤波器传输和反射响应还可以采用特征多项式P（s）、F（s）和E（s）描述：

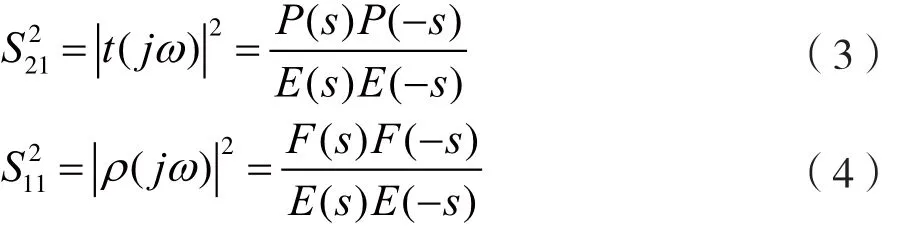
因此，只要能够根据预期目标通过特征函数计算出滤波器对应的特征多项式，则滤波器的性能也随之确定。将理论设计的滤波器转化为实际器件的过程中，需要分析实际滤波器各个谐振单元之间的耦合情况，从而引入耦合矩阵。

耦合矩阵中，各元素代表了对应的谐振单元之间的耦合系数，其阶数对应滤波器的阶数N。通过对耦合矩阵进行相似变换，可以在保持滤波器性能不变的情况下，实现实际拓扑结构的简化。滤波器的耦合矩阵也可以通过其特征多项式综合得出［4-6］。

若设计一款4阶切比雪夫带通滤波器，通带内回波损耗低于-22 dB，在归一化频域［-1.25j，1.25j］添加两个传输零点。采用广义切比雪夫函数作为特征函数，计算得到滤波器对应的特征多项式为：

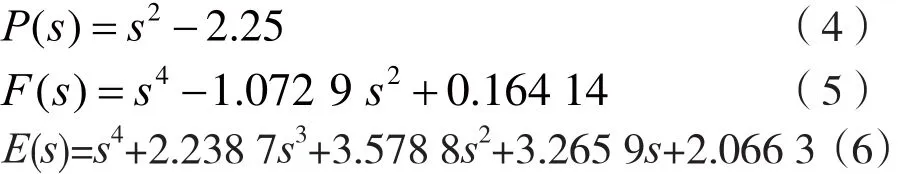
由特征多项式可以计算出滤波器相对应的耦合矩阵Ma：

通过耦合矩阵可以得出该滤波器在频域所对应的归一化频率响应，如图1所示。

从图1可以看出，通带内S22曲线呈等波纹变换，符合切比雪夫函数性质。而引入交叉耦合的设计，使得滤波器引入了两个传输零点，优化了带外抑制效果。

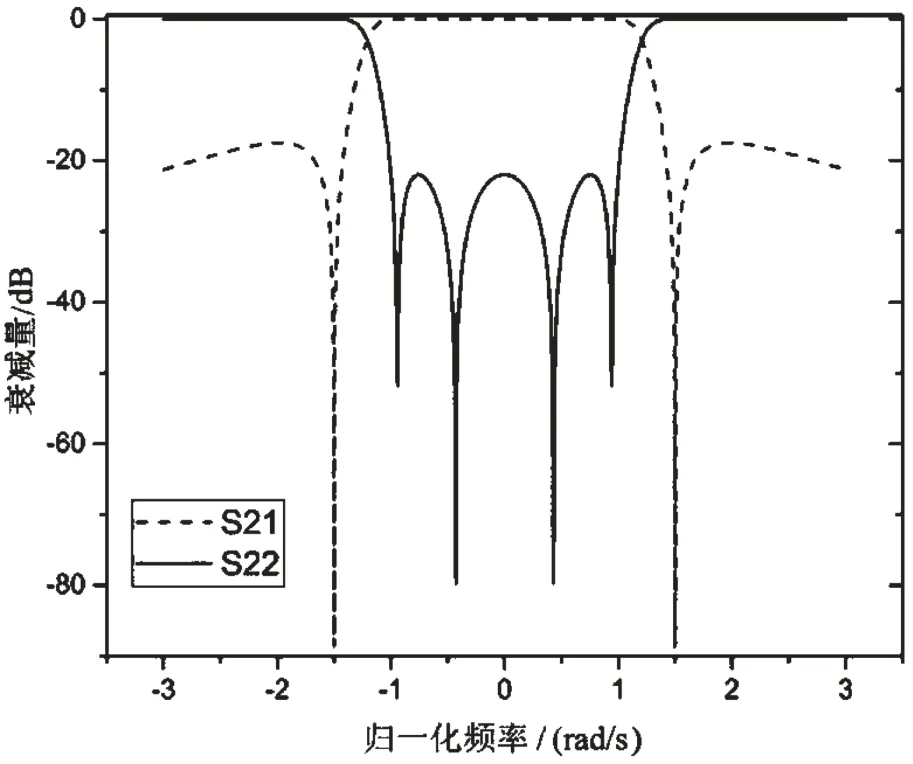
图1　滤波器归一化频率响应曲线

2　非对称双通带滤波器设计

在大多数情况下，实际所需的双通带滤波器带宽不同，或对于通带内回波损耗的要求不同，这时需要设计非对称响应的双通带滤波器。假定非对称双通带滤波器归一化至频域后，其通带范围为［ωLL，ωLH］和［ωRL，ωRH］，仍记双通带归一化至频域域，而低通原型为s=jω（Ω域）。若记Ωz为通带之间分界点，则两频域间转换关系符合关系式为：

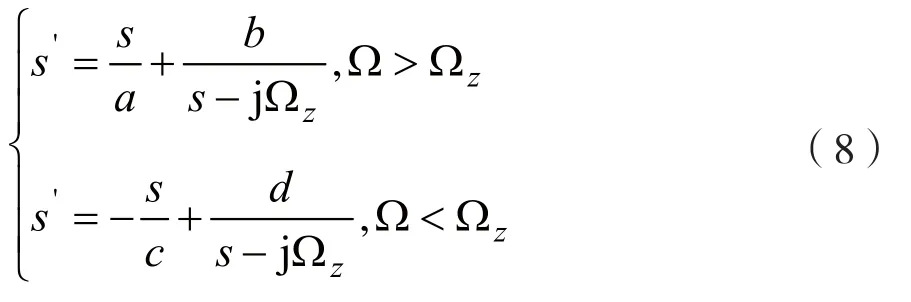
式中，a、b、c和d为待定系数。从低通原型至双通带，之间的频率变换如图2所示。

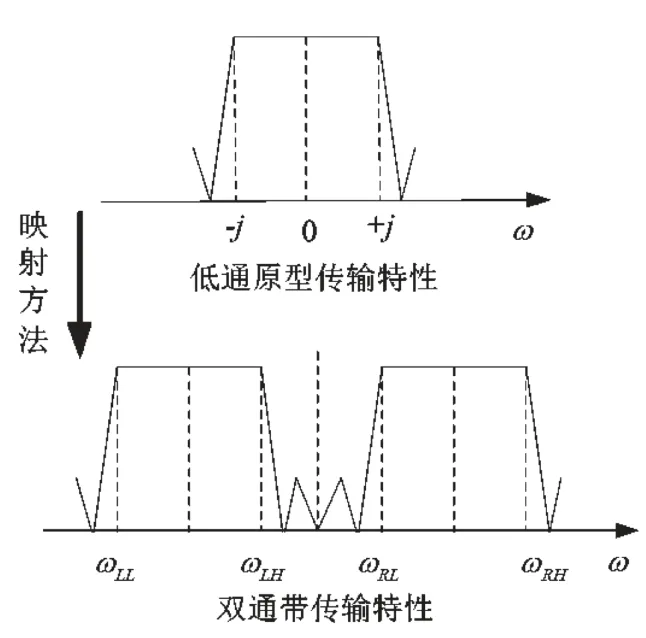
图2　非对称双通带滤波器映射

两频域进行变换，存在边界对应的条件关系，a、b、c和d的值可以通过这个关系来确定。边界对应条件如表1所示。

表1　双通带归一化频域与低通原型对应边界条件

将表1中的数据代入转换公式，便可得出系数，实现频域间的转换。理论上，Ωz可以任意取值，但是不合理的Ωz可能会影响通带间阻带的等波纹特性，因而选取时需要慎重。

文献［7］给出了一类的Ωz计算公式：

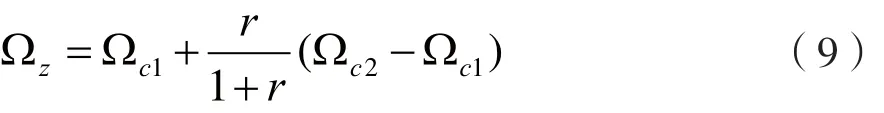
这里，r为两个通带的带宽比值：

例如，现需设计一款8阶非对称双通带滤波器，通带范围为1.2～1.26 GH z和1.3～1.4 GHz。带内的回波损耗为-25 dB，归一化波纹系数εR=1。先确定低通原型中传输零点的位置，若取其为带内回波损耗为-25 dB，则低通原型中反射零点进行频率转化，可以得到对应的非对称双通带滤波器的传输零点Ftz和反射零点

于是，容易求得滤波器对应的特征多项式为：

从而得出滤波器对应的耦合矩阵：

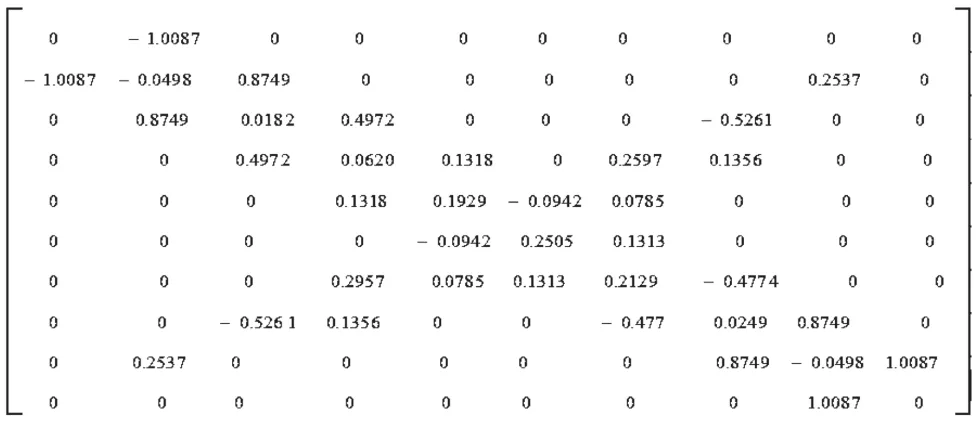
它的频率响应曲线则如图3所示。

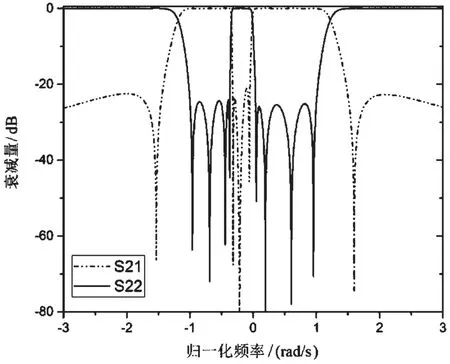
图3　非对称双通带归一化频率响应曲线

从图3可以看出，非对称双通带滤波器在通带内保持了等波纹特性，带外引入的传输零点增强了抑制效果。在两个通带之间，成功添加三个传输零点，不仅使两个通带明显分离，也保证了良好的隔离特性。

为了进一步改进滤波器性能，可以通过数值计算优化分离点。以先前计算的结果为基点，取其附近值进行仿真，比较两个通带之间抑制波纹上极点的值，按照精度选取最为合适。通过优化仿真可以得到，不同分离点对 通带间传输系数的 影响如图4所示。

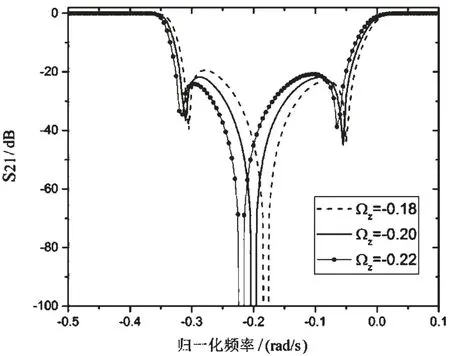
图4　不同分离点对通带间传输系数的影响

由图4可以看出，当Ωz值为-0.2j 时，通带之间两个波纹上的极点基本达到同一水平，且抑制也都位于-20 dB以下。所以，可以认为-0.2j是比较理想的分离点。分离点为-0.2j时，滤波器的传输和反射系数优化结果如图5所示。可以看出，这时非对称双通带滤波器响应达到了非常好的效果。

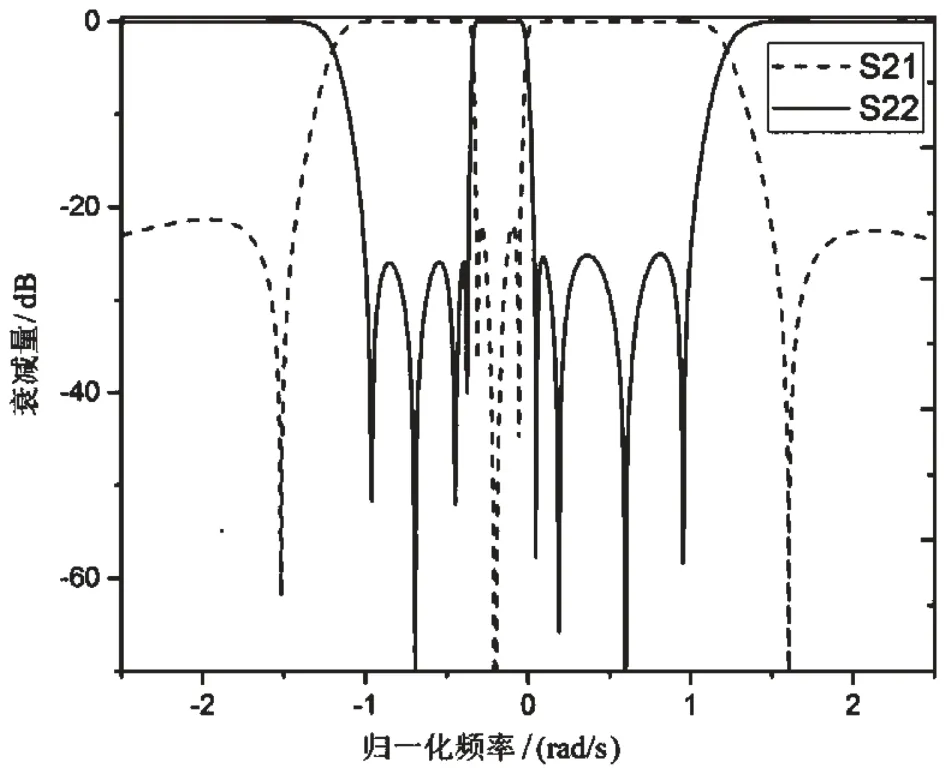
图5　优化后的不对称双通带频率响应曲线

3　设计实例

设计一个双通带滤波器，通频带为2.1～2.4 GHz和2.6～2.9 GHz，带内回波损耗低于-25 dB，两通带间引入两个传输零点［-0.1，0.1］。采用6阶切比雪夫特征函数，综合出对应耦合矩阵：

根据所得的耦合矩阵，可以求得其对应的滤波器归一化频率响应曲线，如图6所示。可以看出，该理论计算完全符合设计期望。

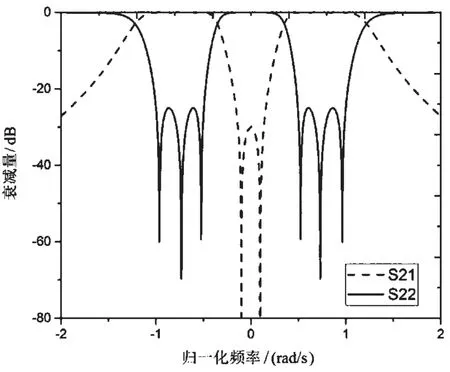
图6　双通带滤波器理论归一化频率响应曲线

通过在Ansoft HFSS13中建模仿真，采用均匀阻抗谐振器（Uniformity Impedance Resonator，UIR）结构实现各谐振器间的耦合，以F4B介质作为基板（εr=2.55，厚度为0.964 mm，损耗角正切0.002），模型结构如图7所示。

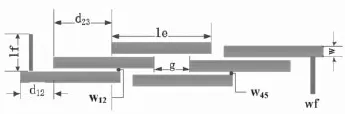
图7　双通带滤波器建模

对模型中各项参数进行优化，最终得到较为适宜的参数尺寸，见表2。

表2　模型中各参数尺寸/mm

仿真得到的滤波器S11和S21曲线如图8所示。从图中可以看出，在2.1～2.4 GHz与2.6～2.9 GHz之间成功实现了两个通带，且通带内S11低于-15 dB，S21在-2 dB附近。可见，在两通带间的传输零点成功将两个通带分离，且保证了通带边沿的陡峭性。两个通带外侧，S21下降很快，陡峭特性也较为良好。

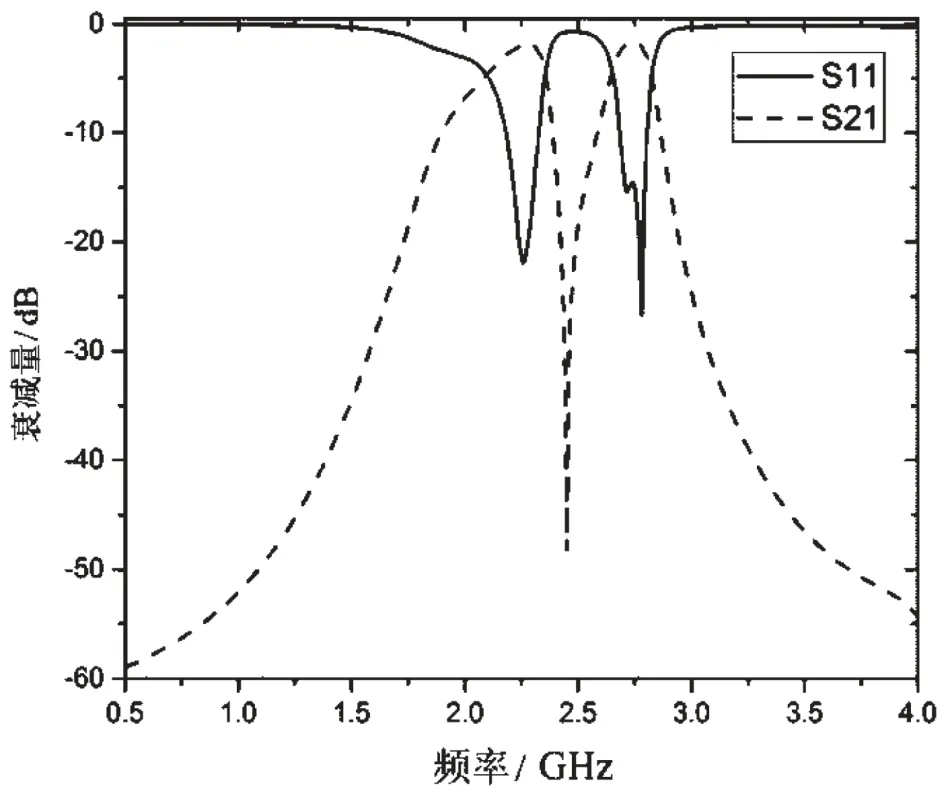
图8　滤波器频率响应曲线

然而，相较理想计算得到的频响曲线，可以看出结果尚存在一些偏差：通带内存在一定的插入损耗，且通带间只出现了一个传输零点。出现这种情况，一方面是由于设计和模型的误差所致；一方面也受到了微带线低Q值的限制。但是，总的来说，设计仿真结果基本达到了预期目标，同时验证了前期理论计算的正确性。

4　结 语

根据所给双通带滤波器的指标要求，采用从低通到带通的对称映射，将已确定的单通带特性扩展至两个子通带，从而实现所需的双通特性。利用耦合矩阵综合方法，对参数进行数值优化，得出双通带滤波器频率响应曲线。在特定频点引入传输零点，大幅提高了滤波器性能，从而使滤波器的设计快速且准确。设计过程清晰、便捷，减少了滤波器后期调试工作量。通过HFSS仿真软件建模仿真，给出了均匀阻抗谐振器结构微带双通带滤波器。仿真结果与文中方法结果基本一致，验证了该计算方法的正确性。

［1］ 程兴，苏涛，梁昌洪.交叉耦合滤波器设计与传输零点的独立性分析［J］.微波学报，2006，（01）：34-38.

CHENG Xing，SU Tao，LIANG Chang-hong.Design and Independence of Transmission Zeros Analysis for Cross-Coupled Filter［J］.Journal of Microwave Science，2006，（01）：34-38.

［2］ Cameron R J，Chandra M，Kudsia.通信系统微波滤波器设基础、设计与应用［M］.王松林，译.北京：电子工业出版社，2012.

Cameron R J，Chandra M，Kudsia.Foundation，Design and Application of Microwave Filters for Communication Systems［M］.WANG Song-lin，translation. Beijing：Publishing House of electronics industry，2012.

［3］ Cameron R J，Rhodes J D.Asymmetric Realization of Dual-mode Band-pass Filter［J］.IEEE Trans. Microwave Tech，1981，（29）：649-655.

［4］ Cameron R J.General Coupling Matrix Synthesis Methods for Cheybeshev Filtering Function［J］.IEEE Trans Microwave Tech，1999，（47）：433-442.

［5］ Cameron R J，Rharish A，Christopher J，et al.Synthesis of Advanced Microwave Filters without Cross-couplings［J］. IEEE Trans Microwave Tech，2002， （50）：2862-2872.

［6］ CameronR J.Advanced Coupling Matrix Synthesis Techniques for Microwave Filter［J］.IEEE Trans. Microwave Tech，2003，（51）：1-10.

［7］ 张德锋.微波双通带滤波器的综合与设计［D］.西安：西安电子科技大学，2010. ZHANG De-feng.Synthesis and Design of Microwave Dual Band Bandpass Filters［D］.Xi'an：Xi'an Electronic and Science University，2010.

［8］ 邓庆文，徐亚军，范童修等.平行耦合微带线滤波器的优化设计方法［J］.微波学报，2014，（S1）：241-244. DENG Qing-wen，XU Ya-jun，FAN Tong-xiu，et al.An Optimization Design of Parallel Coupled Microstrip Filter［J］.Journal of microwaves，2014，（S1）：241-244.

宛新文（1967—），男，硕士，讲师，主要研究方向为宽带通信、微波器件；

张 宇（1992—），男，硕士，主要研究方向为微波电路与器件；

许耀华（1976—），男，硕士，副教授，主要研究方向为无线与移动通信。

李民权（1968—），男，博士，教授，主要研究方向为天线与馈电、微波器件。

Design of Dual-band Filter based on Coupling Analysis

WAN Xin-wen， ZHANG Yu， XU Yao-hua， LI Min-quan
（Key Laboratory of Intelligent Computing and Signal Processing， Ministry of Educaton ， Anhui University， Hefei Anhui 230039， China）

The method based on coupling matrix and assisted by numerical optimization， could achieve dual-band filters with different expected objectives， and the entire design process is clear and convenient. The early-day calculation based on mathematical analysis clearly reduces the workload of simulation，optimization and debugging in the later-on design process. The cross-coupling design could introduce the certain transmission zeros at a specific frequency， thus greatly improving the performance of the filter and making the filter design faster and more accurate. The example design and simulation indicate the correctness of the theoretical calculation. Meanwhile， the experiment results are discussed as well. All this is of important reference value for the design of high-performance dual-band filter.

coupling matrix； dual-band filter； transmission zero； coupling

National Natural Science Foundation of China（No.51477001）

TN713

A

1002-0802（2016）-10-1296-05

10.3969/j.issn.1002-0802.2016.10.006

2016-06-09；

2016-09-12

data：2016-06-09；Revised data：2016-09-12

国家自然科学基金项目（No.51477001）