基于压缩感知的MIMO OFDM系统稀疏信道估计*
2016-11-11丁远晴
丁远晴
(四川警察学院侦查系,四川 泸州 646000)
基于压缩感知的MIMO OFDM系统稀疏信道估计*
丁远晴
(四川警察学院侦查系,四川 泸州 646000)
针对MIMO OFDM系统中时间、频域双选择性衰落信道的估计问题,分析了信道在时延、多普勒域的稀疏特性,提出了一种基于压缩感知的稀疏信道估计方法。通过修改OMP重构算法的迭代终止条件,得到了一种稀疏度未知条件下的改进的OMP算法(简称为I-OMP算法)。与传统最小二乘法相比,改进的OMP算法可以在使用较少导频的条件下获得较好的信道估计性能;与OMP算法相比,在不需要已知时延-多普勒域稀疏度的条件下,改进的OMP算法能够获得复杂度较低、性能较好的信道估计性能。
正交频分复用;双选择性衰落;压缩感知;正交匹配追踪;信道估计
0 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术和多输入多输出(Multi-Input Multi-Output,MIMO)技术是第四代乃至第五代移动通信系统的关键技术[1]。OFDM具有传输速率快、频谱资源利用率高和有效抵抗多径干扰等优点;MIMO技术能有效提高无线信道容量。但在高速移动性快衰落环境中,引发的多普勒频移扩展会破坏OFDM子载波间的正交性,造成子载波间干扰(Inter Carrier Interference,ICI)。同时,无线信道的多径效应使信道具有频率选择性,是快衰落环境下严重影响系统性能的因素之一。快时变信道具有时间和频率两方面的选择性,因此增加了待估计信道状态信息的数量。
利用少量导频来准确估计时频双选择性信道的问题,实际上是已知条件较少而待解未知数多的问题。同时,对无线宽带多径信道进行物理测量的结果表明,信道具有稀疏特性[2]。在此基础上,一些学者提出运用压缩感知理论[3],以较少的导频符号有效重构该稀疏信号,进而得到理想的信道估计。文献[4]提出了一种在慢衰落信道中,基于导频辅助的压缩信道感知(Compressed Channel Sensing,CCS)算法。算法利用了信道在时延域的稀疏性,但受限于慢衰落信道情况,并没有考虑快衰落环境下,信道在多普勒域的稀疏性。所以,若将该算法运用到快衰落信道中,在频率的采样位置与实际信道变化的频率范围方面将出现偏差,容易引起功率混叠与泄露,影响信道稀疏性,导致信道重构性能不好。文献[5]基于分析超宽带(Ultra Wideband,UWB)系统信道的稀疏特性,建立了一种统计信道模型,利用压缩感知恢复算法重构信道的稀疏系数。
本文利用MIMO OFDM时频双选择性衰落信道在时延-多普勒域的稀疏性,研究OMP算法的迭代停止条件,提出一种不需要知道信道在时延-多普勒域的稀疏度值的I-OMP算法。算法使用导频数量少,能够提高频谱资源利用率。此外,算法未使用信道稀疏度值,在与OMP算法信道估计性能相当的前提下,扩大了OMP算法的普适性。本文中,diag(·)表示对角化,(·)T和(·)H分别表示转置和共轭转置,vec(·)表示将矩阵以列堆叠进行向量化,表示向上取整,⊗表示Kronecker积。
1 系统模型
MIMO OFDM系统中,假设发射天线数和接收天线数分别为Nt和Nr,t=1,…,Nt表示发射天线序号,r=1,…,Nr表示接收天线序号。用n=1,…,N表示OFDM符号序号,每个符号有K个子载波,k=1,…,K表示子载波序号。在子载波k1,k1,…,kp上放置P(P<K)个导频符号。对于第n个OFDM符号而言,第t根发射天线上第k个子载波所发送的信号表示为第(r,t)天线对间的第k个子载波的信道状态信息表示为那么,第r根接收天线所接收到的P个导频符号为:

在一个OFDM符号内,若信道的变化是线性的,那么导频所受的子载波间干扰可认为是小于噪声水平的。非导频子载波的ICI污染,如式(1)中的部分,可被视为加性噪声[6-7]。用表示噪声向量与ICI部分的和。于是,式(1)可另写为:

定义最大多普勒频移vmax,Td表示单个OFDM符号块持续时间,W表示带宽,τmax表示时延扩展。假设不同(r,t)天线对间的信道满足独立同分布,那么第r个接收天线与第t个发送天线间的高移动性信道在时延-多普勒域表示为:

令:

则:
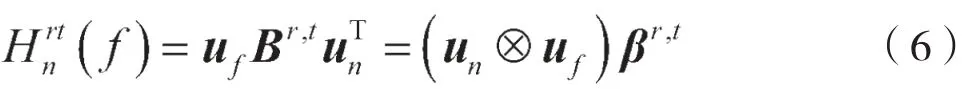
其中,Br,t是由第(r,t)天线对间双选择性信道在时延-多普勒域的稀疏系数所组成的矩阵,其维数由可分辨时延数和多普勒频移数决定,为L×(2M+1)。矩阵具体展开为:

定义βr,t=vec(Br,t)表示将矩阵Br,t进行向量化,即将Br,t中的列进行堆叠,形成一个长度为L(2M+1)的列向量。将式(6)带入式(2)可得:

2 信道估计算法
2.1 压缩感知综述
压缩感知技术[8]是对稀疏性信号以低于奈奎斯特采样率的速率进行采样。所谓稀疏性信号是指信号本身是稀疏的或在某个变换域是稀疏的。与传统信号采样技术不同,压缩感知实现信号抽样的同时,也对信号进行了压缩。利用最优化方法,接收端能够以很高的概率重构原信号。压缩感知的测量模型可表示为:

式中,H表示V×1维列向量,Ψ为V×V变换基矩阵,β为V×1维列向量。若β只有S个非零值,其余均为0或近似于0的值,且S<<V,则H在Ψ域是稀疏的。X表示U×V维与Ψ不相关的观测矩阵,Y表示测量后的结果,是由测量值组成的U×1维向量,其中V>U≥cSlog2(V/S),c为常数[9]。接收端利用X、Ψ和Y重建信号β,然而求解的未知数数目多于方程组数目,因此β的解不唯一,需要根据一定的准则找出最优解。
2.2 稀疏信道估计
正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[10]的基本思想是在每一次迭代过程中,从过完备原子库即恢复矩阵XΨ中,选择与信号Y最相关的一列作为原子,并将所选原子进行正交化处理,构成正交空间,再计算出信号在空间上的投影分量和残余分量;下一次迭代中对残余分量作相同的分解处理。通过一定次数的迭代,原信号被分解为一些原子的线性组合形式,各分量的加权系数则构成重构信号。该算法复杂度较低,有利于实时重构稀疏信道系数。
OMP算法中的迭代次数是根据信道稀疏度来确定的,因此算法要求稀疏度值是已知的或者有预设值。对于慢衰落信道,一个OFDM符号内信道冲激响应不随时间变化或者变化缓慢,这些信道的稀疏度值自然也可认为是不变的。因此,慢衰落信道下,OMP算法估计性能较好。而在实际快衰落信道环境下,信道在时延-多普勒域的稀疏度很难确定,盲目预设信道的稀疏度值往往达不到预期的效果。
图1给出了不同稀疏度值的先验信息下,对于式(8)使用OMP算法的信道估计性能。不难看出,预设的稀疏度值小,将导致算法运算迭代次数过少,估计性能降低;而预设的稀疏度值过大,所引起的迭代次数过多,将带来不必要的运算,增加算法复杂度。因此,先验信息稀疏度值会影响重构算法的效能。本文通过研究传统OMP算法的迭代终止条件,提出一种稀疏度未知情况下的OMP算法,简称为I-OMP算法,可有效解决这个问题。

图1 不同稀疏度值时基于OMP算法的信道估计误差比较
从OMP算法迭代过程可知,被重构的信道稀疏系数的稳定性可由接收信号残余分量的能量大小来衡量。信号残余能量越小,说明重构完成度越高。也就是说,在快衰落信道中,可以用相邻两次迭代中信号残余分量的能量差作为迭代停止条件。当能量差值小于任意小的阈值时,停止迭代,此时可认为重构完成。
I-OMP算法具体描述如下:
第一,初始化参数,设恢复矩阵T=XΨ,索引值集合Λ=∅,残差r0=Y,相邻两次迭代残余信号的能量差Δ0=||r0||。
第二,定义η为一阈值常数,表示相邻两次迭代间残余信号的能量差的最小值。η取值较小,当Δi≥η时,进行迭代:
(2)合并索引集Λi=Λi-1∪{λi},此时索引集Λi中元素个数为i;
(3)利用最小二乘(Least Square,LS)算法获得新的估计该估计值在Λi之外的地方均为零,在Λi内的估计为:

其中,TΛi为P×i维矩阵,包含T矩阵中索引为Λi的所有列,(·)†表示伪逆运算。
(4)对观测估计值和信号残差进行更新:

3 仿真结果及分析
为比较I-OMP算法、传统频域LS算法以及OMP算法在快衰落信道估计方面性能的不同,本文进行了以下仿真。考虑一个TD-LTE系统上行链路,时频双选择性快衰落信道模型是3GPP TS 36.101、36.104等标准中定义的多径衰落模型测试信道。系统仿真参数配置为:系统天线配置为2Rx2Tx(二发二收);带宽W为1.4 MHz,OFDM中的子载波数K为128;一个子帧包含14个OFDM符号,长度Td为1 ms;子载波频率fc为2.6 GHz;最大时延扩展τmax为5 μs;最大多普勒频移vmax为300 Hz,即收发端的最大相对速度约为125 km/h;迭代中的停止阈值常数η=10-6。本文主要仿真验证基于压缩感知的稀疏信道估计可行性和I-OMP算法的可行性。
3.1 基于压缩感知的稀疏信道估计可行性
仿真分析了导频数量不同的情况下,分别采用传统频域LS算法和OMP算法估计导频位置对应的信道信息。其中,频域LS算法基于公式(2),且导频位置均匀分布;OMP算法导频位置随机分布,预设稀疏度值为12,结果如图2所示。从二者的估计均方误差(MSE)可看出,传统LS算法性能较差,在增加导频数或提高性噪比条件下仍不见好转,LS算法几乎失效。这是由于在多根发射天线系统中,有Nr×P个已知关系式,而带估计值的数目却有Nr×Nt×P个。这种情况下,不论导频个数如何取值,方程都是病态的,LS算法并不能准确估计唯一的信道信息矩阵。而相同导频数情况下,OMP算法能够较好地重构稀疏信道系数,信噪比提高时,OMP算法的性能随之改善。信噪比一定的情况下,导频数量增加,OMP算法的估计误差相应减小。说明时频双选择性快衰落信道中,基于压缩感知的时延-多普勒域稀疏信道估计具有可行性。
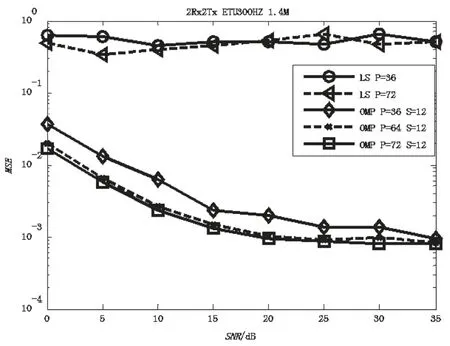
图2 频域LS算法和OMP算法性能比较
3.2 I-OMP算法的可行性
图3给出了导频数量为64,导频位置随机选取,在不同的稀疏度S情况下的OMP算法信道估计性能。显然,S=12和S=20时,OMP算法的性能与S=6时有较大提升;在中高信噪比条件下,性能提升更为明显;而S=20时的算法性能相较于S=12时提升并不明显;当迭代达到一定程度,算法性能趋于收敛。正如前面的分析,OMP算法中预设的稀疏度值S会直接影响算法迭代次数,继而影响算法的效能。
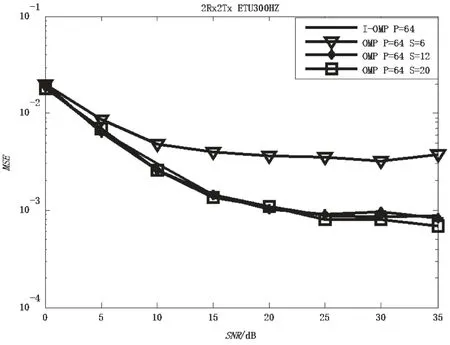
图3 OMP算法与I-OMP算法性能比较
同时,图3也对I-OMP算法与OMP算法的信道估计MSE进行了比较。从图3中可以看出,I-OMP算法性能与性能最优的OMP算法相当,并且I-OMP算法不需要人为假设稀疏度值,能够较好地控制算法复杂度。这样算法达到较优的估计性能的同时,复杂度亦较小,不失为提升性能和效率的一种好方法。
4 结 语
本文研究了MIMO OFDM时频双选择性信道在时延-多普勒域的稀疏表示,并对传统OMP算法重构信道信息的准确性和复杂性进行了分析。在此基础上,通过修改OMP重构算法迭代条件,提出了一种I-OMP算法,其无需已知信道在时延-多普勒域稀疏度,解决了实际快衰落信道在时延-多普勒域稀疏度难以确定的问题,避免了由于设置不同稀疏度值所引起的算法性能不稳定。通过仿真比较频域LS算法和OMP算法,验证了利用压缩感知原理和OMP重构算法解决稀疏信道估计的可行性。通过对I-OMP算法与OMP算法的仿真比较可知,采用I-OMP算法进行信道估计的性能与OMP算法最优估计性能相当,而I-OMP算法的复杂度相对较小,提高了重构算法的效能。
[1] 尤肖虎,潘志文,高西奇,等.5G移动通信发展趋势与若干关键技术[J].中国科学:信息科学,2014,(05):551-563.
YOU Xiao-hu,PAN Zhi-wen,GAO Xi-qi,et al.The Development and Key Technologies of 5G Mobile Communication[J].SCIENCE CHINA Information Sciences,2014,(05):551-563.
[2] Raghavan V,Hariharan G,Sayeed A M.Capacity of Sparse Multipath Channels in the Ultra-Wideband Regime[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(03):357-371.
[3] Candes E J,Wakin M B.An Introduction to Compressive Sampling[J].IEEE Signal Processing Magazine,2008,25(02):21-30.
[4] Bajwa W U,Haupt J,Sayeed A M,et al.Compressed Channel Sensing:A New Approach to Estimating Sparse Multipath Channels[J].Proceedings of the IEEE,2010,98(06):1058-1076.
[5] 何雪云,潘林,彭伟刚.压缩感知在稀疏信道估计中的应用[J].通信技术,2011,44(09):27-29. HE Xue-yun,PAN Lin,PENG Wei-gang.Application of Compressive Sensing Theory in Sparse Channel Estimation[J].Communication Technology,2011,44(09):27-29.
[6] Mostofi Y,Cox D C.ICI Mitigation for Pilot-aided OFDM Mobile Systems[J].Wireless Communications,2005, 4(02):765-774.
[7] El H S Y,Sezginer S.Fast Varying Channel Estimation in Downlink LTE Systems[J].Personal Indoor & Mobile Radio Communications IEEE International Symposium on,2010:608-613.
[8] Donoho D L.Compressed Sensing[J].Information Theory,2006,52(04):1289-1306.
[9] Candes E J,Romberg J,Tao T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].Information Theory,2006,52(02):489-509.
[10] Tropp J,Gilbert A C.Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J].Information Theory,2008,53(12):4655-4666.

丁远晴(1992—),女,硕士,助教,主要研究方向为无线通信系统的信道估计技术。
Compressed Sensing based Sparse Channel Estimation in MIMO OFDM Systems
DING Yuan-qing
(Department of Investigation, Sichuan Police College, Luzhou Sichuan 646000, China)
To solve the channel estimation problem for time- and frequency-selective fading MIMO OFDM systems, the features of the channel in Delay and Doppler domain are analyzed. A new method of sparse channel estimation based on compressive sensing(CS) is proposed. The Improved OMP(I-OMP) algorithm works in channel of unknown sparse degrees by modifying the condition of termination in iteration in OMP recovery algorithm. Simulations have shown that the I-OMP estimation has much better performance with a few pilots than conventional least square estimation; and compared with Orthogonal Matching Pursuit(OMP)estimation, the I-OMP algorithm can obtain the same good performance steadily, whose complexity is lower,without knowing the sparse degrees of channel in Delay-Doppler domain.
orthogonal frequency division multiplexing(OFDM); double selective fading; compressive sensing(CS); orthogonal matching pursuit(OMP); channel estimation
TN911.23
A
1002-0802(2016)-10-1287-05
10.3969/j.issn.1002-0802.2016.10.004
2016-06-13;
2016-09-22
data:2016-06-13;Revised data:2016-09-22
