粘弹结构模态损耗因子分析的修正模态应变能法

孙宝,孙大刚,李占龙,燕碧娟,王军

(1.太原科技大学机械工程学院,山西太原030024;2.西安理工大学机械与精密仪器工程学院,陕西西安710048)

粘弹结构模态损耗因子分析的修正模态应变能法

孙宝1,孙大刚1,李占龙2,燕碧娟1,王军1

(1.太原科技大学机械工程学院,山西太原030024;2.西安理工大学机械与精密仪器工程学院,陕西西安710048)

为了研究粘弹结构的阻尼特性,采用传统变形能理论建立了粘弹结构结构损耗因子的计算模型,并对相关阻尼参数进行了优化分析;通过研究传统模态应变能法与已有3种改进方法的原理及其相互关系,提出了一种新的修正模态应变能方法,新方法中修正因子随不同阶次模态损耗因子的幅值而变化。以一种四参数原型系统为依据,通过对4种模态应变能法的误差分析表明新修正方法对结构损耗因子与固有频率的计算误差最小;选取两个算例,通过对结构损耗因子与固有频率采用修正模态应变能法、变形能法、传统模态应变能法及相关文献有限元法的计算结果表明:修正模态应变能法可以满足工程设计的要求,且计算误差最小;修正模态应变能法可为粘弹结构阻尼特性与结构设计及改进等领域的研究提供一定的理论参考。

振动与波;模态应变能法;粘弹阻尼结构;模态损耗因子;固有频率

DOI:10.3969/j.issn.1000-1093.2016.01.023

0 引言

阻尼技术是目前使用比较广泛的一种对振动加以控制的方法,该技术利用阻尼耗能的原理,充分发挥阻尼在减振、降噪中的作用,从而提高机械结构的抗振性,降低机械产品的噪声,增强机械与机械系统的动态稳定性[1]。粘弹性复合结构便是采用约束阻尼处理技术来增大结构损耗因子,避免结构强度、刚度的损失,最终达到高效振动响应控制与结构承载功能一体化的目的。因此,研究粘弹性复合结构的阻尼耗散性能自然成为当前工程领域减振降噪技术中一类比较重要的课题[2]。

许多学者对该问题做了大量的研究,主要分为解析法与数值法。解析法包括:复刚度法、变形能理论等。数值法包括:复特征值法、模态应变能法与有限单元法等。文献[1]采用传统变形能理论分析了粘弹阻尼结构的阻尼性能,但该理论需要大量的经验数据,且在具体的工程应用中计算误差偏大。为了更好地适用于工程领域,目前较多采用了有限元法[3-12]。文献[3]采用复特征值法在阻尼状态下求解运动方程,得到的特征值与特征向量均为复数,计算复杂性极高,文献[4]利用有限元模态应变能(MSE)法找出阻尼结构的模态参数,计算简单、快速。虽然避免了大量多特征值的计算,但随着粘弹性成分的提高,该方法的误差增大,往往使得计算结果比精确解要偏小。文献[5]对传统的模态应变能法进行了改进,将粘弹性材料的模量用复模量的绝对值替换,提出一种改进的模态应变能(AVMSE)法。文献[6]中对AVMSE法做了进一步的改进,提出一种计算模态损耗因子更为精确的方法(RMSE法)。

综上所述,变形能理论虽然给出了模态损耗因子与固有频率的理论分析计算,可为阻尼层的优化设计,结构改进等问题提供理论参考,但该方法依赖于大量的经验数据,往往导致计算误差较大。为了避免变形能理论中使用大量的经验数据,本文对比分析了传统模态应变能法、MSE及已有模态应变能修正方法AVMSE、RMSE的原理及其相互关系,研究发现两种修正方法中粘弹结构不同阶次模态的修正因子均相同,而相同的修正因子可能带来过量修正或修正不足。而我们知道,一般地,不同阶次的模态粘弹结构应该具有不同的损耗因子[7],根据这一思想,本文在RMSE法的基础上,提出了一种基于模态损耗因子幅值变化的新修正方法(ACMSE).选取两个算例,通过与变形能理论对比,表明新修正模态应变能法对粘弹复合结构模态损耗因子及固有频率的计算误差更小,精度更高。

1 变形能理论

粘弹约束阻尼结构是采用上下层为强度较高的弹性材料(如钢、铝合金),中间层采用粘弹性阻尼材料(如橡胶、塑料)复合而成的一种约束阻尼结构[1],如图1所示。

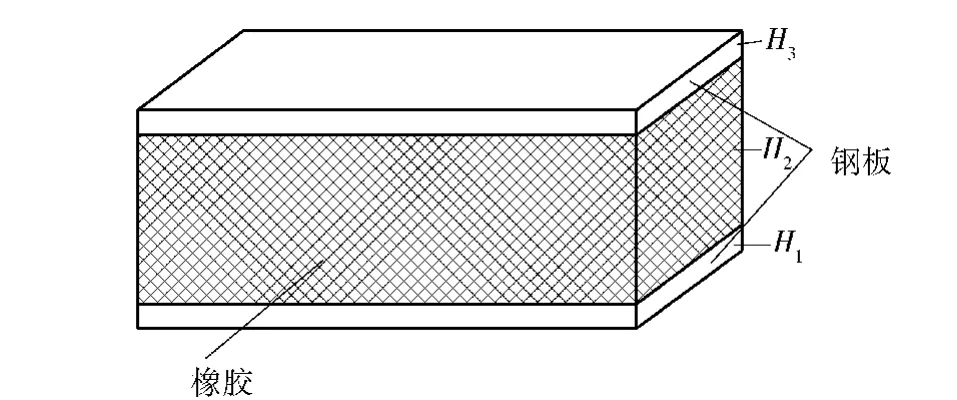
图1 粘弹约束阻尼结构Fig.1 Viscoelastic constrained damping structure

结构损耗因子η可表示为结构耗散能和总的弹性变形能的比值:

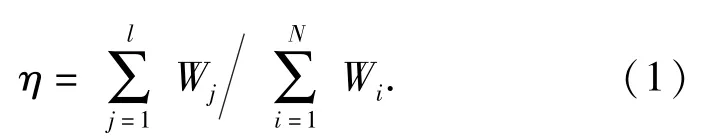
采取图2所示的一般约束阻尼结构形式。外层是需要消振的任意结构,内层是受到外层包容的约束结构,阻尼层处于内、外层之间。

戴德沛[1]采用Kerwin的理论假设提出:若仅考虑阻尼附加结构的横向弯曲振动,对任何附加阻尼结构的结构损耗因子η均可表示为

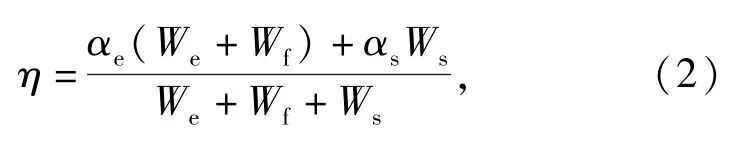
式中:αe为耗能结构的拉伸损耗因子;αs为耗能结构的剪切损耗因子;We为拉伸变形能;Wf为弯曲变形能;Ws为阻尼层弹性剪切变形能。

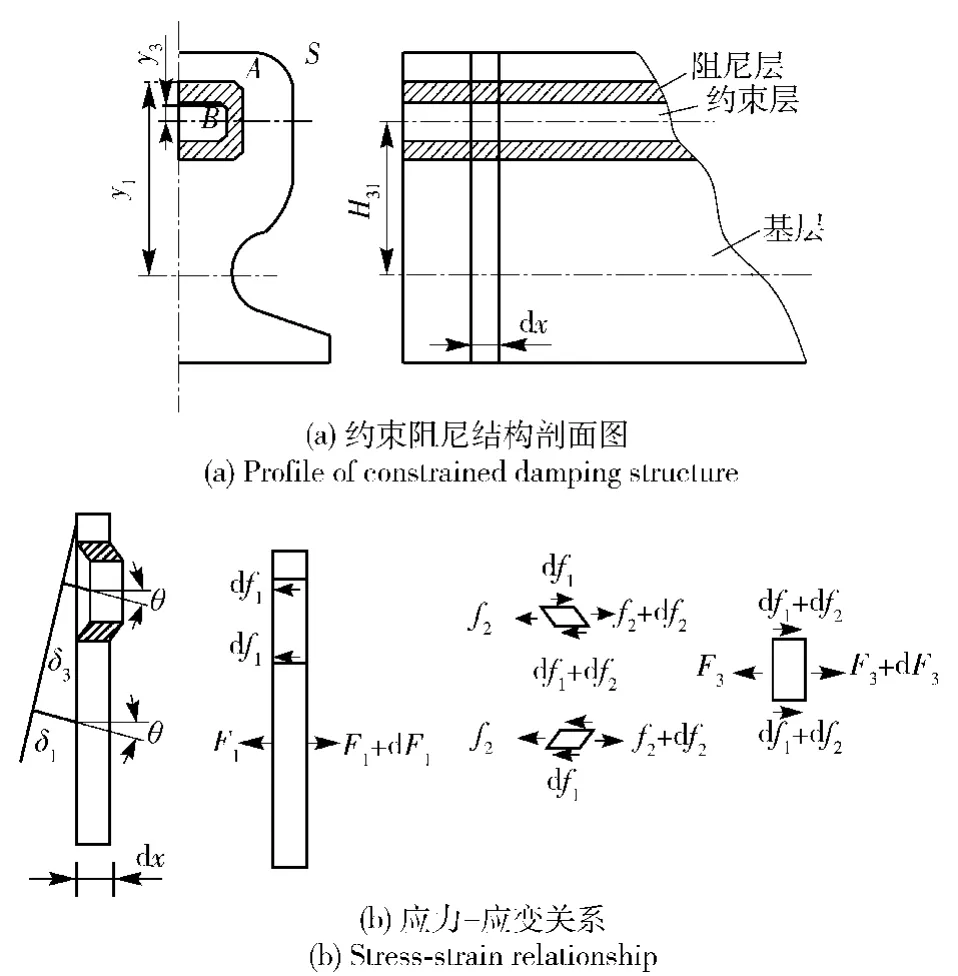
图2 约束阻尼结构应力-应变关系Fig.2 Stress-strain relationship of constrained damping structure

进一步推导、简化,最后可得结构损耗因子η:

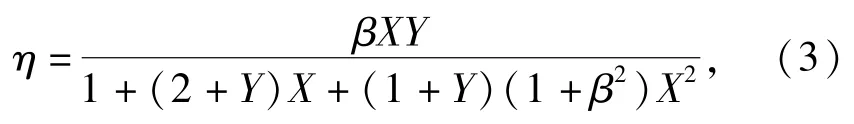
式中:β为粘弹材料的损耗因子。

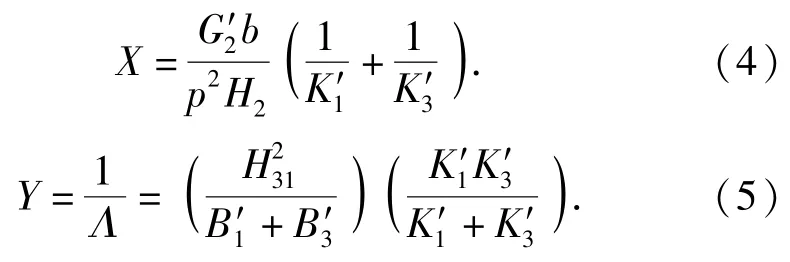
可见,对于一个粘弹约束阻尼结构,利用变形能法求得的结构损耗因子η为材料损耗因子β、剪切参数X及刚度参数Y的一个空间曲面。

2 变形能理论的阻尼性能分析

图3给出利用变形能理论计算粘弹约束阻尼结构损耗因子的计算框图。依据工程经验,将阻尼层厚度H2取合理的变化区间,迭代计算便可获得最大结构损耗因子η=ηmax,同时也可得到ηmax下所需的一系列阻尼参数的最优值。

2.1 刚度参数Y的优化分析

一般地,刚度参数Y的设计方程为

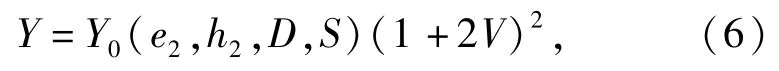
式中:V=H2/H3+λH1;e2=E2/E1为杨氏模量比; h2=H2/H1为厚度比;D=b/A为尺寸比;S=H/A为尺寸比。

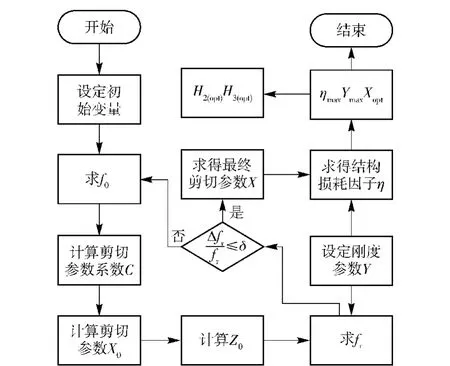
图3 约束阻尼结构损耗因子计算框图Fig.3 Block diagram of loss factor calculation of constrained damping structure

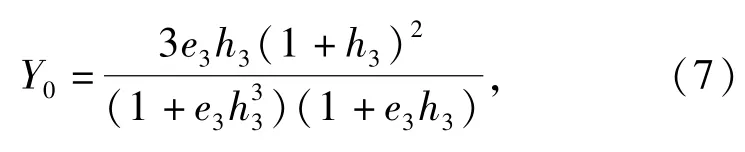
式中:e3=E3/E1为约束层与基层的杨氏模量比; h3=H3/H1为约束层与基层的厚度比。

依据工程经验,图4给出对应于两个不同e3值,约束层厚度比h3分别等于0.1、0.5、1、2情况下,刚度参数Y关于阻尼层厚度H2的变化曲线,从图4中可直观看出Y与阻尼层厚度H2的变化规律。

对比表明:对于一个粘弹约束阻尼结构,固定约束层厚度比h3,结构刚度参数Y会随着阻尼层厚度H2的增加而变大。固定约束层杨氏模量比e3,当阻尼层厚度H2不变时,结构刚度参数Y会随着约束层厚度比h3的增加而增大。

2.2 剪切参数X的优化分析

剪切参数X的计算步骤如下:

1)依据工程经验设定阻尼层厚度H2的变化区间:H2∈[a,b],相关材料参数,结构参数。计算结构的固有频率

2)计算剪切参数系数

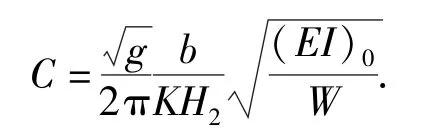
3)设Z=0,令fr=f0,这里fr表示组合结构在r阶模态下的固有频率,计算剪切参数X0:

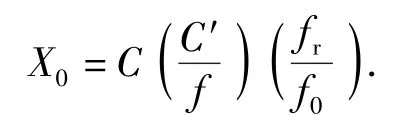
4)令X=X0,给定β,求Z0:

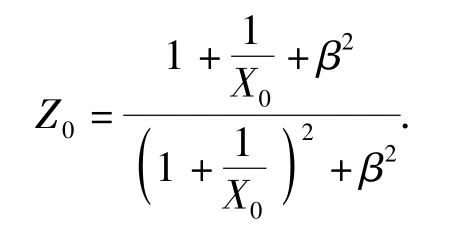
5)由Z0求

6)第一轮计算完之后,第二轮迭代开始,计算新的fr,此时fr≠f0,重复进行最后得到剪切参数X,若逐次迭代计算新的fr满足条件Δfr/fr≤0.1%,则计算终止。

图5给出剪切参数X关于阻尼层厚度H2的变化趋势,图中可直观看出阻尼层厚度对剪切参数的影响作用。

对比表明:对于一个粘弹约束阻尼结构,当固定阻尼层厚度H2时,剪切参数X会随着频率的增大而逐渐变小。对于固定的频率,随着阻尼层厚度H2的增加,剪切参数X逐渐变小。

2.3 η与X、Y的耦联关系

由(3)式,为了讨论的方便,本文选取常见的两类材料损耗因子β值。固定材料损耗因子β,图6给出当β分别等于0.2、2的情况下,η对X、Y的优化曲面。

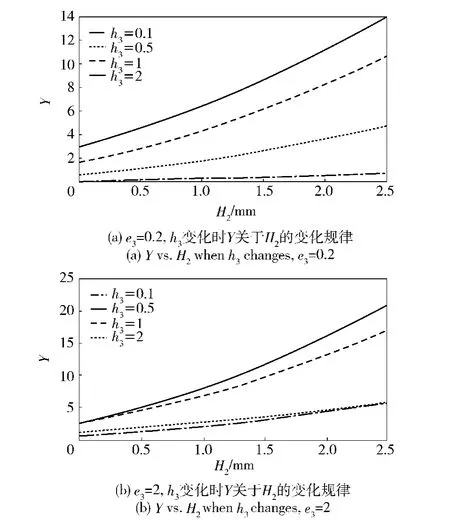
图4 Y与H2的函数关系曲线Fig.4 Function relation curve between Y and H2

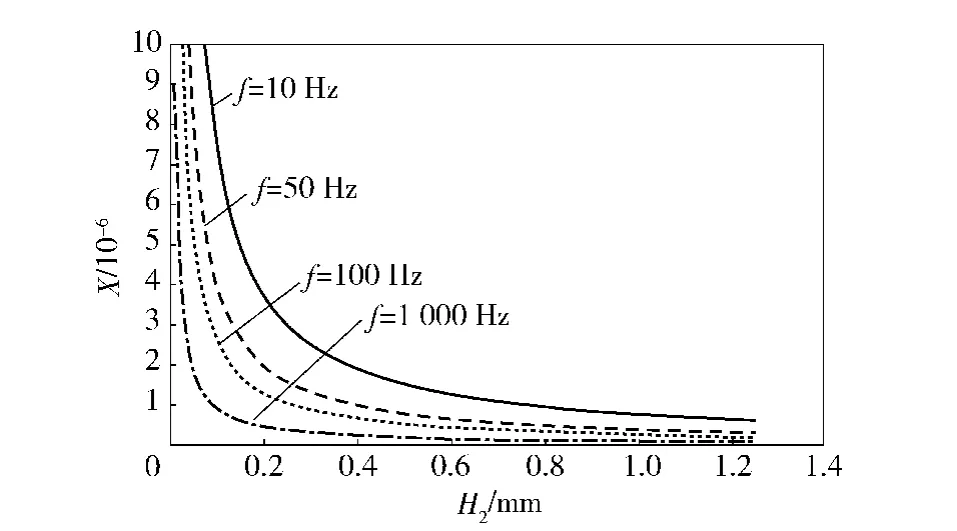
图5 X与H2的函数关系曲线Fig.5 Function relation curve between X and H2

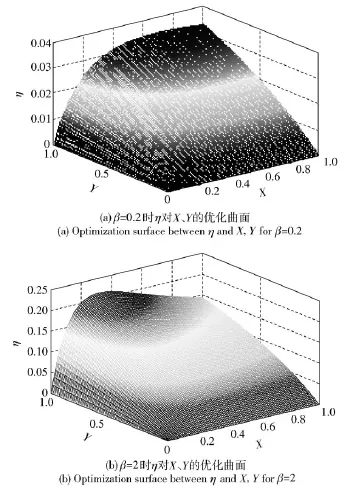
图6 η对X、Y的优化曲面Fig.6 Optimized surface of η and X,Y

综上所述,由图4～图6可得出以下结论:

1)对于一个粘弹约束阻尼结构,当固定材料损耗因子β时,结构损耗因子η是由剪切参数X与刚度参数Y共同作用的结果。为了获得最大的结构损耗因子ηmax,需对剪切参数、刚度参数进行合理的优化分析。

2)剪切参数对阻尼结构耗散性能影响显著,计算中若选取不合理,将导致结构损耗因子η仅是最大值的10-3～10-2[1].另外,η与刚度参数Y成正比,为了得到ηmax,可通过改变结构件的外形尺寸,来加大Y的取值。但并不是Y越大越好,从上述剪切参数的优化分析可知,Y与X又成反比例关系。分析中需要一定的经验数据。

3)阻尼结构层间厚度是影响结构阻尼性能的重要因素之一,在分析各阻尼参数相互间关系的基础上,通过合理的优化,可以得到最大结构损耗因子ηmax.

3 修正模态应变能法

3.1 传统MSE方法

MSE法将粘弹复合结构的实特征向量Φr近似替代复特征向量得到第r阶的近似复圆频率为

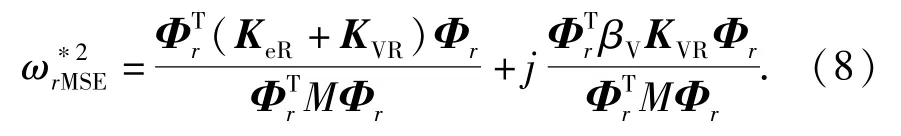
MSE方法的第r阶的近似模态损耗因子ηrMSE为

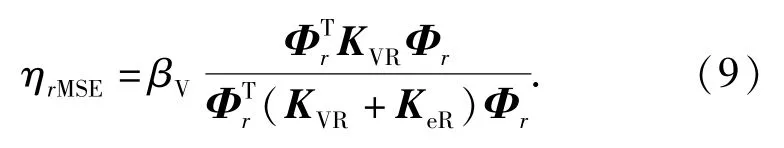
3.2 模态应变能法AVMSE、RMSE

MSE法中,实部与虚部的分离过程并未考虑粘弹性滞后对结构振型的影响。当结构矩阵中虚刚度比例增大时,计算误差较大。考虑到虚刚度的影响,对复刚度取绝对值进行修正,利用实模态Φr近似替代复合结构模态从而求得AVMSE法的第r阶近似复圆频率[6]:

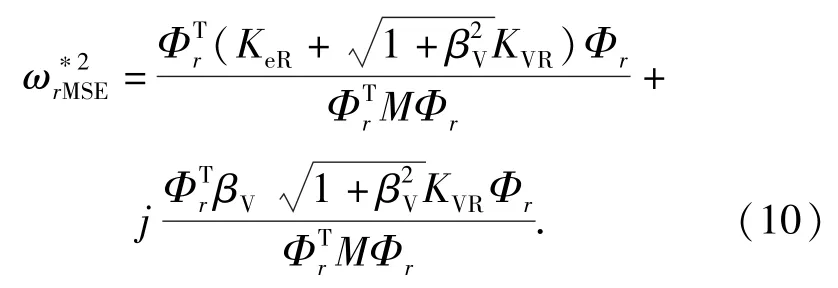
经过计算最后可得AVMSE法的第r阶近似模态损耗因子ηrAVMSE:

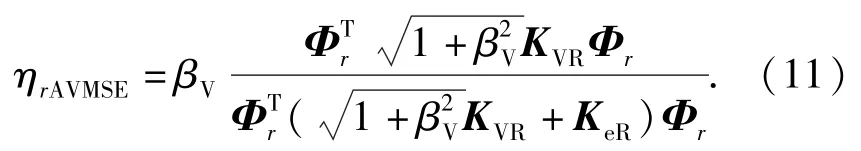
模态应变能损耗因子的计算受到刚度矩阵与特征向量的双重修正,AVMSE法可能产生过量修正。Rongong提出一种修正方法,将(11)式除以一个修正因子从而获得了RMSE法的第r阶近似模态损耗因子:

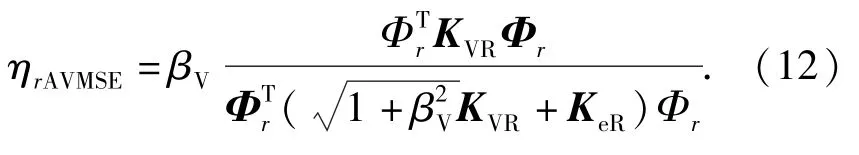
通过比较(11)式与(12)式,RMSE法的第r阶近似模态损耗因子ηrRMSE又可表示为

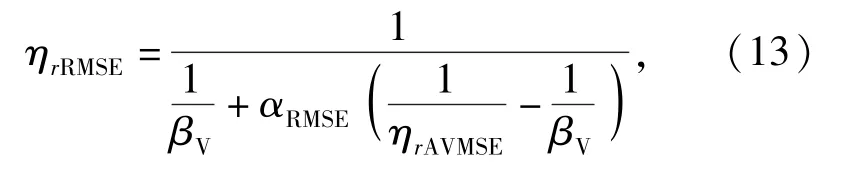
RMSE法的第r阶模态的近似损圆频率ωrRMSE为

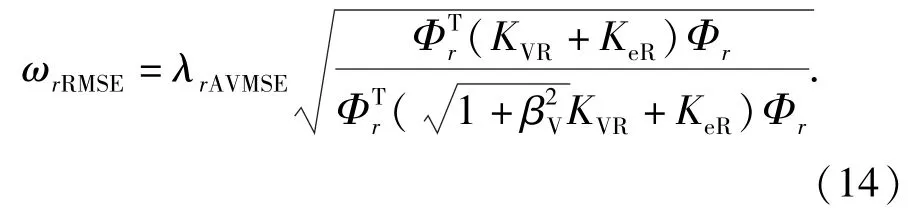
整理可得另一种表达形式为

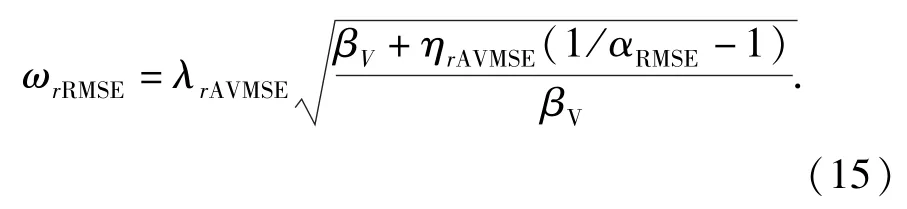
3.3 修正模态应变能法ACMSE

对于不同的模态阶次,粘弹复合结构理论上应具有不同的损耗因子[7]。但AVMSE法和RMSE法所提出的修正因子均相同,可能造成修正不足或过量修正。为此,本文在RMSE方法修正因子αrRMSE的基础上,结合0≤ηr≤βV,设计并提出一种新的修正因子αrACMSE,该因子随结构损耗因子的幅值而变化,有可能提高计算精度。取

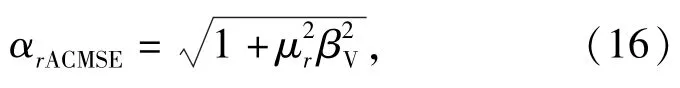
由(13)式可得ACMSE法第r阶近似模态损耗因子ηrACMSE为

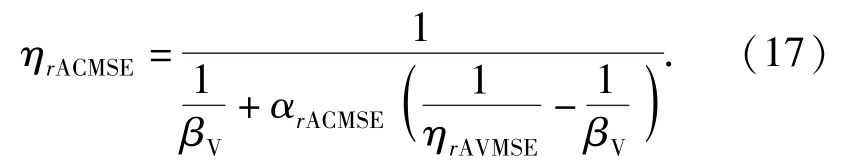
类似于RMSE法,同理可得ACMSE法的第r阶近似圆频率ωrACMSE为

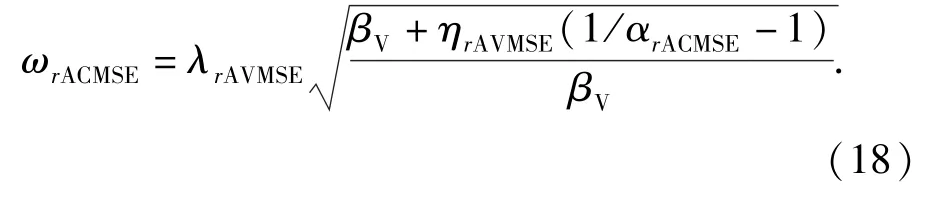
4 修正模态应变能法误差分析

本文选取Torvik等提出的可等效为一种粘弹性夹层梁(板)的四参数原型系统作为依据分析几种模态应变能法的误差[7]。如图7所示。

由粘弹性-弹性原理计算系统的复刚度K*:

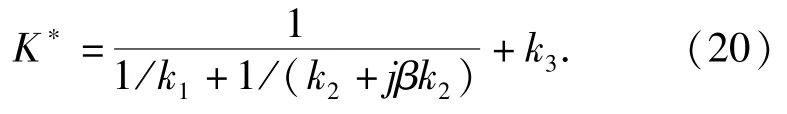
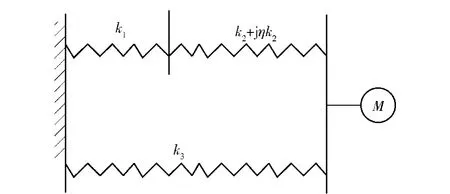
图7 四参数原型系统Fig.7 Four-parameter prototype system

系统复刚度的虚部与实部的比值可求得系统损耗因子ηs:

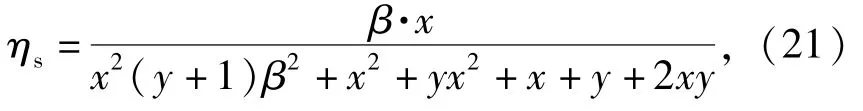
式中:χ=k2/k1;y=k3/k1;β为复刚度弹簧损耗因子。

系统齐次解的计算得到系统的固有圆频率ωs:

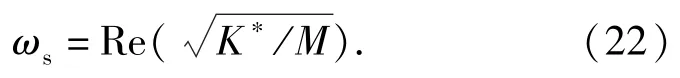
MSE法是将复刚度弹性模量用实部代替,绝对值模态应变能法AVMSE将复刚度弹性模量用其绝对值替代,RMSE在AVMSE法的基础上提出一种新的修正因子。上述3种模态应变能法的结构损耗因子与固有圆频率可分别表示如下:

式中:χ=k2/k1,y=k3/k1为刚度比;z=k1/M;α=

分析AVMSE、RMSE法中修正因子的特点,本文提出一种新的修正模态应变能法ACMSE.新方法中修正因子α＇随系统不同模态阶次的损耗因子的幅值而变化,计算误差更小。由已有模态应变能的推导过程可得ACMSE法的结构损耗因子与固有圆频率如下:

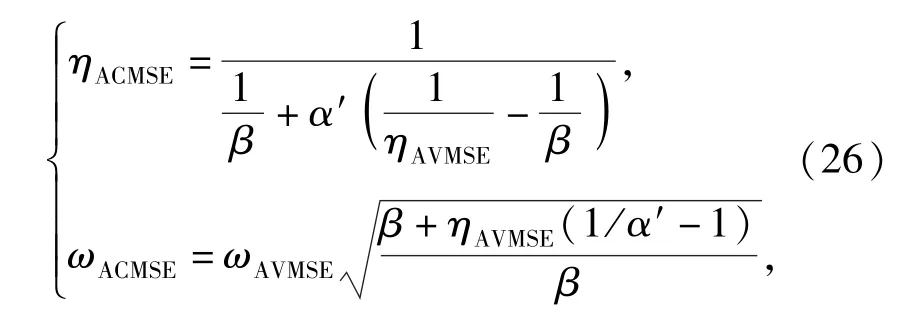
可见四参数原型系统中损耗因子η与刚度比χ、y及复弹簧损耗因子β三个变量有关。固有频率ω与刚度比χ、y、复弹簧损耗因子β及z四变量有关,为了分析方便,本文取z为常量。

为了比较4种模态应变能法的计算误差。本文取刚度比χ、y范围为0.01～100,包含了刚度比的4个数量级变化;复弹簧损耗因子β范围为0～2,表明了常见的一些粘弹材料的损耗因子[7]。图8和图9分别给出4种模态应变能法对结构损耗因子与固有频率的计算相对误差曲线。

比较图8、图9,从中可以得出以下结论:

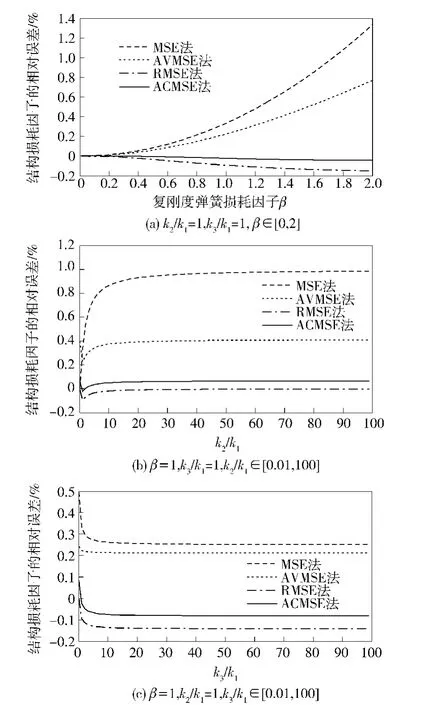
图8 4种模态应变能法计算损耗因子的相对误差Fig.8 Relative errors of loss factors calculated by four modals strain energy methods

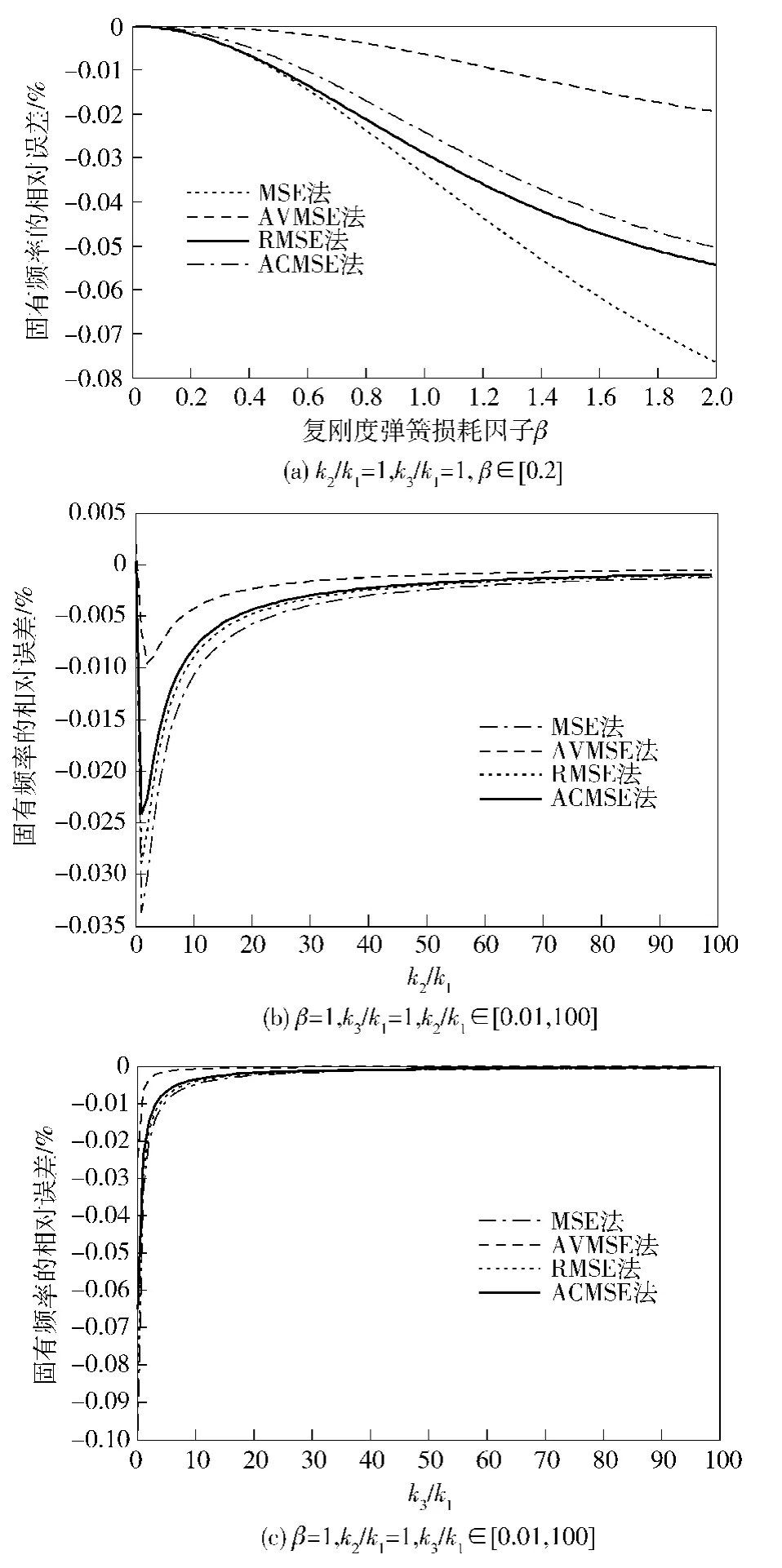
图9 4种模态应变能法计算固有频率的相对误差Fig.9 Relative errors of natural frequencies calculated by four modals strain energy methods

1)固定刚度比χ,y,4种方法计算结构损耗因子与固有频率的误差均随材料损耗因子的增加而增大。其中MSE方法的误差表现尤为明显,因此很有必要对其进行修正。

2)比较AVMSE、RMSE法,本文修正方法ACMSE对结构损耗因子的计算误差最小,且对固有频率的计算误差仅大于AVMSE法。

3)取定材料损耗因子β,当分别固定刚度比k3/k1与k2/k1时,ACMSE法对结构损耗因子的计算误差最小,且随着刚度比值的增加,误差趋于稳定。

4)总体来看,随着固定刚度比的增加,几种方法的计算误差非常接近,且总体趋于稳定。对固有频率的计算ACMSE法的计算误差仅大于AVMSE法。

综上所述,通过对损耗因子及固有频率的计算误差分析比较,4种模态应变能法中新模态应变能法ACMSE计算结构损耗因子及固有频率是最有效的一种改进方法。

5 材料损耗因子的DMA实验测试

2.3节在固定材料损耗因子β分别等于0.2和2的前提下给出了结构损耗因子η关于剪切参数X及刚度参数Y的耦联关系。3.3节对几种模态应变能法所作的误差分析中选取材料损耗因子β的范围为0～2.上述内容在材料损耗因子β取为定值的情况下开展研究,然而我们知道对于阻尼橡胶材料,其损耗因子关于温度与频率具有一定的非线性,为了更加准确地研究粘弹复合结构的阻尼特性,需要考虑阻尼材料损耗因子的这一非线性质。

为此,本文采用德国NETZSCH DMA242C动态机械分析仪对粘弹复合结构常用橡胶材料开展动态性能的测试分析。动态机械分析仪DMA242C能够对试件温度进行实时控制,在试件表面施加动态变化的激励力,可方便准确地获取试件材料损耗因子关于温度与频率的相关动态特性。依据该分析仪的工作原理,本文选取三点弯曲方式作为实验项目进行相关测试。实验过程见图10.

图10 动态机械分析仪DMA242CFig.10 Dynamic mechanical analyzer DMA242C

粘弹性橡胶材料的复拉伸模量E*可通过下式获得:

式中:l为弯曲长度;b为橡胶件宽度;h为橡胶件高度;F为激励力;a*为橡胶件变形量。

橡胶材料损耗因子β可表示为

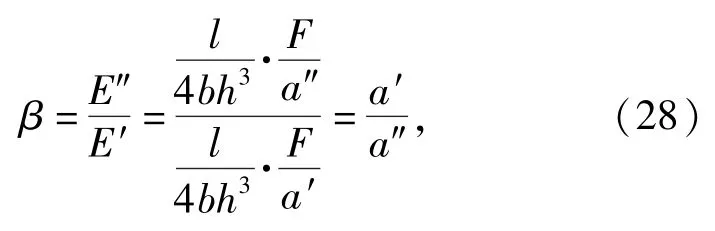
式中:E"为损耗弹性模量;E＇为储存弹性模量,a"为动态位移虚部;a＇为动态位移实部。

测试前制作橡胶试件外形尺寸为l×b×h=40 mm× 10 mm×4 mm,程控软件确认为三点弯曲分析模式,实验过程温度选取 -30℃ ～90℃,设定温度按4℃/min速率递增。分析频率取 4种频率2 Hz、3.33 Hz、5 Hz和10 Hz.当环境温度适合且保持不变30 min后,测试工作开始。整个实验在动态机械分析仪程序监控下自动完成。最后可获得该阻尼橡胶材料的动态参量变化曲线,分别见图11、图12、图13.

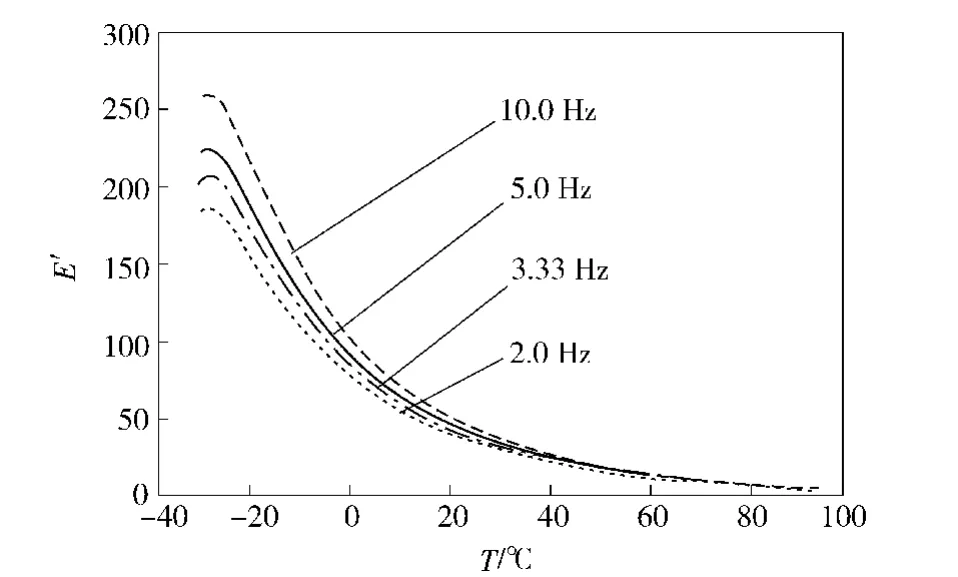
图11 E＇的温度-频率动态特性Fig.11 Temperature and frequency characteristics of E＇

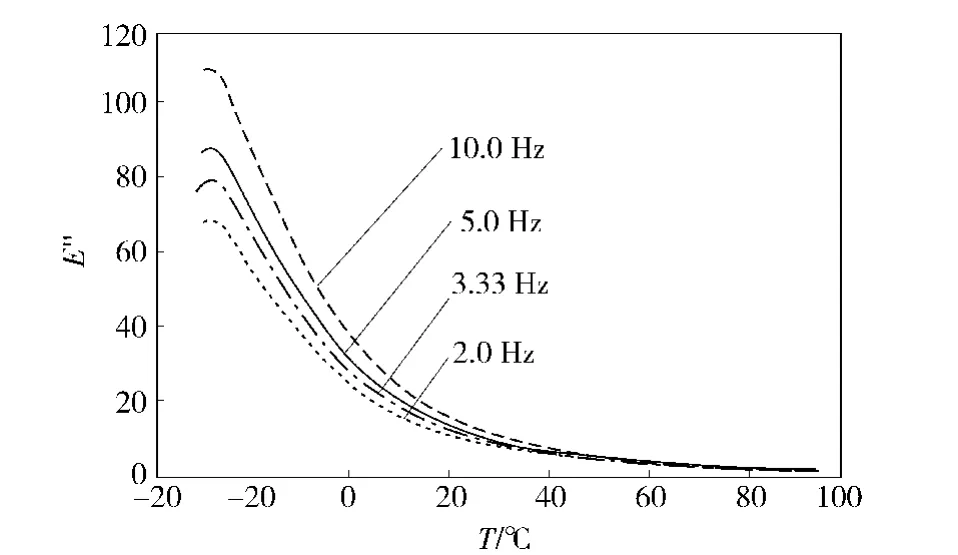
图12 E"的温度-频率动态特性Fig.12 Temperature and frequency characteristics of E"

从图13可以看出:材料损耗因子具有一定的非线性质,在设定温度及频率下,该橡胶试样材料损耗因子β的变化范围大致为0.10～0.42;当频率一定时,β随温度的增加而降低;当温度一定时,β随频率的增大而增加,意味着对橡胶表面施加动态变化的激励力时,橡胶本身β会随之发生变化,这一过程也充分体现了橡胶作为阻尼材料所起阻尼效应是明显的。

通过DMA实验测试获得了阻尼橡胶材料损耗因子β关于温度及频率的动态特性。实验结果可为本文关于材料损耗因子β的确定及选取提供一个有力的实验依据,同时为了进一步体现材料阻尼的非线特性,将这一特性引入到阻尼结构阻尼性能的研究中,以后仍需针对这一问题进行进一步深入的研究。

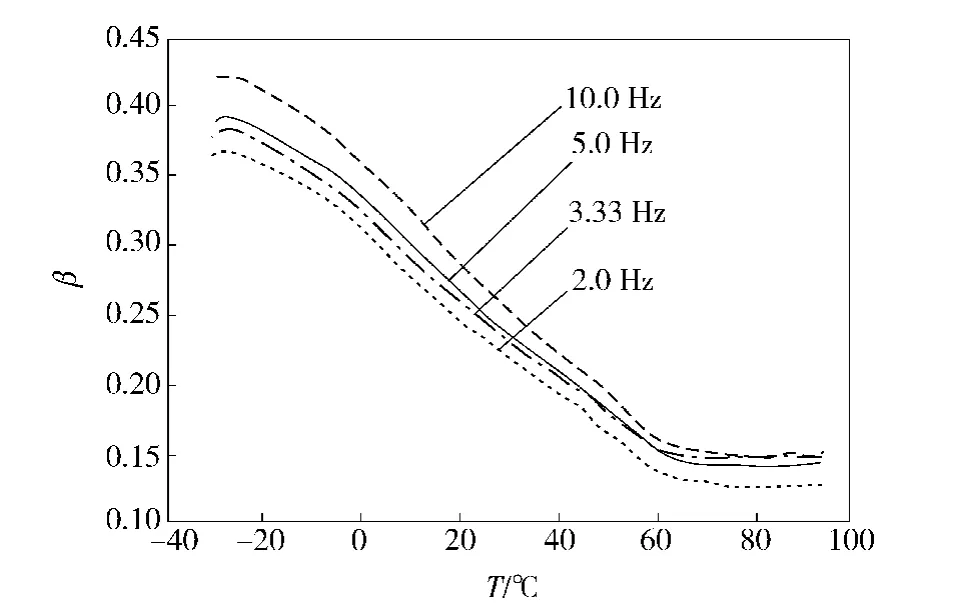
图13 β的温度-频率动态特性Fig.13 Temperature and frequency characteristics of β

6 算例验证

6.1 算例1

本文利用文献[8]中关于边界条件影响的结论:边界条件的改变并不会对最大模态损耗因子ηmax产生影响,但当结构出现最大模态损耗因子ηmax时,固有频率ωmax发生移动。根据此观点,本文采用新模态应变能法ACMSE,仅考虑对边简支的约束阻尼板计算粘弹约束阻尼结构不同模态阶次的模态损耗因子及固有频率。算例如下:

取四边间支约束阻尼结构,夹层板为长0.5 m,宽0.3 mm,粘弹材料的损耗因子β=1.0.材料主要参数如下表1所示。

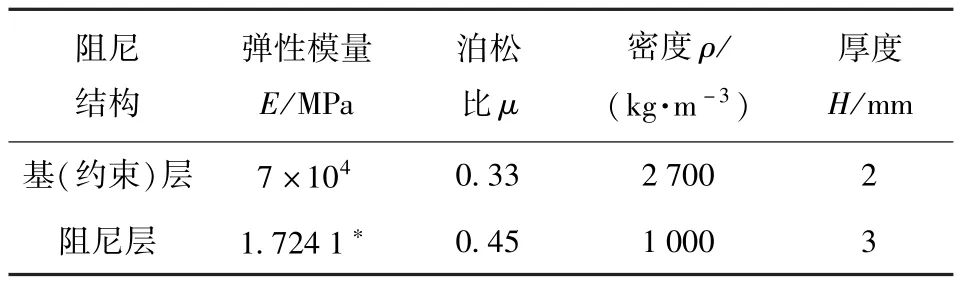
表1 夹层板的主要材料参数Tab.1 The main material parameters of sandwich plate

算例1采用两端部固支矩形截面阻尼夹层结构,总层数为3层。应用有限元进行建模时,阻尼层采用Hex 8六面体单元,弹性层采用CQuad 4板单元。为了确保层间位移的协调,本文定义了板单元节点与对应实体单元节点间的多点约束单元(Rbe 2),有限元模型示意图如下。

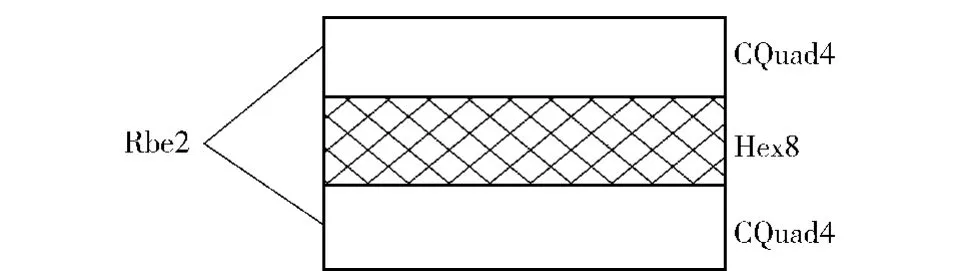
图14 阻尼夹层结构有限元模型Fig.14 Damped sandwich structural finite element model

表2给出了利用修正模态应变能法ACMSE与变形能法对该结构损耗因子和固有频率的计算结果。利用Ansys软件进行模态分析,计算得到模态损耗因子,并与文献[9]中Ansys结果进行对比。分析模型为三维实体,单元为SOLID45.实体单元具有8个节点,每个节点具有3个自由度,分别是χ、y、z的平动自由度,输入的材料特性为各向同性。

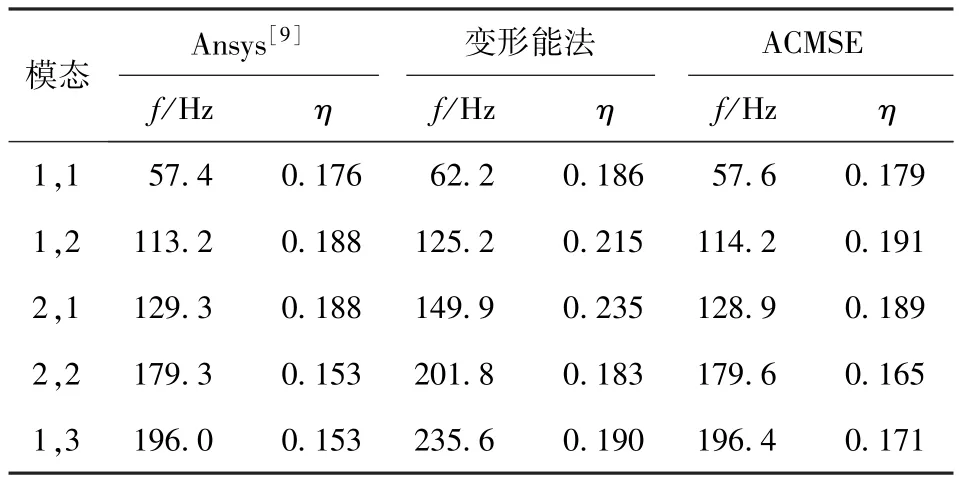
表2 ACMSE与变形能法计算结果的比较Tab.2 The comparison of calculated results of ACMSE and deformation energy method

通过对比表2的计算结果,表明:变形能法与ACMSE法的计算结果还是非常接近的。相比Ansys的分析结果,两种方法的固有频率与结构损耗因子的误差均小于5%.从而说明了变形能法与ACMSE法的合理性,且能满足一些工程设计的要求。

通过与文献[9]中Ansys的分析结果对比:本文提出的修正模态应变能法ACMSE较传统的变形能法对模态损耗因子与固有频率的计算误差明显要小。分析该误差的主要原因可能是传统的变形能法只考虑了阻尼层的剪切效应,而ACMSE法在有限元计算时对阻尼层既考虑了剪切效应,又考虑了挤压效应。另外变形能计算中需要一定的经验数据,也有可能导致计算误差的偏大。

6.2 算例2

为了验证ACMSE法的精确性,选取Johnson给出的一个算例[10]:0.304 8 m×0.348 0 m的各向同性的四边简支夹层板结构,阻尼层厚度为0.254 mm,剪切模量为0.896 MPa、泊松比均为μ=0.49,密度为ρc=999 g/cm3,损耗因子β=0.50.基层、约束层厚度为0.762 mm,弹性模量均为E=68.9 GPa,泊松比均为μ=0.30,密度均为ρf=2 740 g/cm3.

表3给出了利用传统MSE法,新模态应变能修正法ACMSE对粘弹复合结构模态损耗因子及固有频率计算结果。为了便于结果对比,利用Ansys软件进行模态分析,分析模型为三维实体,单元为SOLID45.

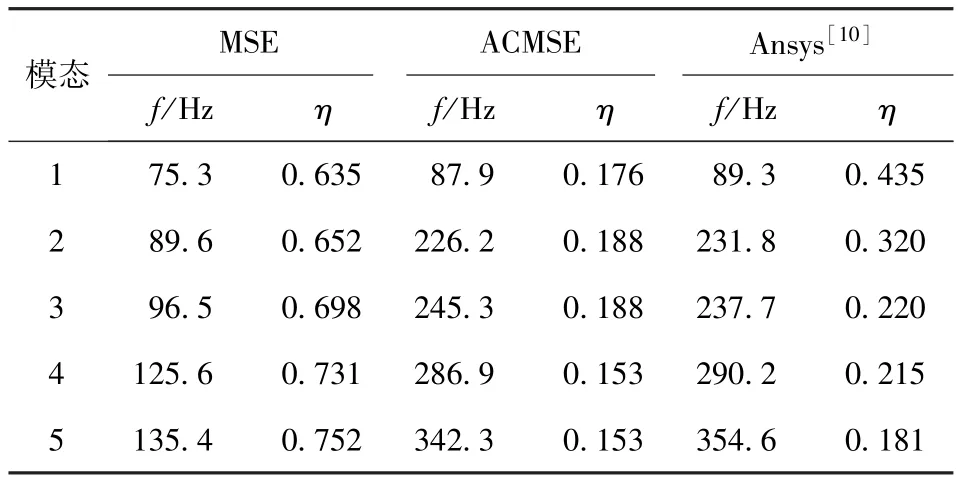
表3 本文结果与Ansys计算结果的比较Tab.3 The comparison ofcalculated results of the proposed method and Ansys method

计算结果表明:通过与文献[10]中Ansys的分析结果对比,相比传统模态应变能法MSE,修正方法ACMSE的模态损耗因子与固有频率的计算误差明显减小,且最小误差可减小至15%左右;同时由于修正方法相比传统MSE避免了复数的计算,计算效率也有了显著的提高;修正后的新模态应变能法能够满足工程设计的需求,同时也验证了本文提出的新方法的合理性与正确性。

7 结论

1)对传统变形能理论做了相关讨论,从理论分析的角度说明变形能法在粘弹约束阻尼结构阻尼性能分析中的应用,可为一些工程优化设计,结构改进等理论问题提供一定的参考。但同时也表明该方法过多依赖大量的经验数据,计算误差偏大。

2)研究了已有模态应变能法 MSE、AVMSE、RMSE的特点及相互关系,在RMSE法的基础上,修正模态应变能法,提出了一种基于模态损耗因子幅值变化的新模态应变能法ACMSE.

3)选取两个算例计算粘弹结构损耗因子及固有频率,通过有限元分析,分别对比ACMSE与传统变形能法,ACMSE与传统模态应变能法MSE.表明修正方法的计算误差最小,验证了该方法的正确性。

4)本文对于材料损耗因子β的确定,为了分析计算的方便,仅是依据经验取为定值。实际上材料损耗因子β具有一定的非线性变化。本文仅通过DMA实验初步地探讨了这一过程,后续应针对材料阻尼的非线特性及其在结构阻尼性能分析中的应用进行更深入的研究。

References)

[1]戴德沛.阻尼减振降噪技术[M].西安:西安交通大学出版社,1986:1-30.DAI De-pei.Damping vibration noise reductiontechnology[M].Xi' an:Xi'an Jiaotong University Press,1986:1-30.(in Chinese)

[2]桂洪斌,赵德有,郑云龙.粘弹性阻尼层结构动力学问题有限元综述[J].振动与冲击,2001,20(1):44-47.GUI Hong-bin,ZHAO De-you,ZHENG Yun-long.A review finite element method analyzing dynamic problem of structure with viscoelastic damped layer[J].Journal of Vibration and Shock,2001,20(1):44-47.(in Chinese)

[3]王正兴,代会军.粘弹性阻尼材料在板结构中的优化计算[J].噪声与振动控制,2000,18(6):21-30.WANG Zheng-xing,DAI hui-jun.An optimized computation for damping elastic plank structure[J].Noise and Vibration Control,2000,18(6):21-30.(in Chinese)

[4]申颜利,杨庆山,田玉基.模态应变能方法精确性和适用性研究[J].工程力学,2008,25(6):18-21.SHEN Yan-li,YANG Qing-shan,TIAN Yu-ji.Study of accuracy and applicability of modal strain enegy method[J].Engineering Mechanics,2008,25(6):18-21.(in Chinese)

[5]吕刚,陆锋,张景绘.桁架结构阻尼控制的绝对值模态应变能法[J].宇航学报,1999,20(2):113-118.LYU Gang,LU Feng,ZHANG Jing-hui.Absolute value modal strain energy method for viscoelastic damping control of truss structure[J].Journal of Astronautics,1999,20(2):112-116.(in Chinese)

[6]Rongong J A.Reducing vibration levels using‘smart joint'concepts[C]//International Conference on Noise and Vibration Engineering.Leuven,Belgium:ISMA,2000.

[7]李世其,张针粒,朱文革.计算粘弹结构动力学参数的新模态应变能法[J].噪声与振动控制,2011,12(18):47-52.LI Shi-qi,ZHANG Zhen-li,ZHU Wen-ge.A new modal strain energy method for analyzing dynamic parameters of viscoelastic structures[J].Noise and Vibration Control,2011,12(18):47-52.(in Chinese)

[8]郭中泽,罗景润,陈裕泽.约束阻尼结构的模态损耗因子计算的一种修正方法[J].兵工学报,2006,27(6):1064-1067.GUO Zhong-ze,LUO Jing-run,CHEN Yu-ze.An improved method of predicting the modal loss factors of constrained damping structure[J].Acta Armamentarii,2006,27(6):1064-1067.(in Chinese)

[9]郑辉,陈瑞石,骆振黄.基于三维弹性理论的约束结构振动阻尼特性分析[J].应用力学学报,1996,13(2):13-21.ZHENG Hui,CHEN Rui-shi,LUO Zhen-huang.Study of the vibratory damping properties of constrained damping panels based on 3-dimensional elasticity theoy[J].Journal of Applied Mechanics,1996,13(2):13-21.(in Chinese)

[10]Johnson C D,Kienholz D A.Finite element prediction of damping in structures with constrained layers[J].AIAA Journal,1982,20 (9):1284-1290.

[11]燕碧娟,孙大刚,宋勇.基于振动能耗散的间隔阻尼层合支重轮参数优化[J].农业工程学报,2011,27(1):175-179.YAN Bi-juan,SUN Da-gang,SONG Yong.Parameters optimization of segmented damping composite bogie wheel using vibration energy dissipation[J].Transactions of the Chinese Society of Agricultural Engineering,2011,27(1):175-179.(in Chinese)

[12]Mehata C R,Tewari V K.Damping characteristics of seat cushion materials for tractor ride comfort[J].Journal of Terramchanics,2010,47(6):401-406.

Modified Modal Strain Energy Method for Analysis of Modal Loss Factors of Viscoelastic Structure

SUN Bao1,SUN Da-gang1,LI Zhan-long2,YAN Bi-juan1,WANG Jun1
(1.School of Applied Science,Taiyuan University of Science and Technology,Taiyuan 030024,Shanxi,China; 2.School of Mechanical and Precision Instrument Engineering,Xi'an University of Technology,Xi'an 710048,Shaanxi,China)

In order to study the damping characteristics of viscoelastic structures,a calculation model of the viscoelastic structure structure loss factor is established using the traditional deformation energy method,and the optimized analysis is carried out on the relevant damping parameters.A modified modal strain method is proposed by analyzing the principles and correlation of the traditional modal strain method and several improved methods.In the proposed modified method,the modifying factor of the viscoelastic constrained damping structure changes with the amplitude of modal loss factor.The prototype system with four parameters is selected as the basis,and the calculated errors of the proposed modified modal strain method and other methods are analyzed,respectively.The results show that calculated error of the proposed method is the least.Two examples are selected to calculate the modal loss factor and natural frequency of the viscoelastic composite structure.The calculated results of the modified modal strain energy method,the deformation energy method,the traditional modal strain energy method and the finite element method show that the modified modal strain energy method can meet the requirements of engineering design,and the calculation error is the least.The modified modal strain energy method can provide a theo-retical reference for the research on the damping characteristics of viscoelastic structures and structural design.

vibration and wave;modal strain energy method;viscoelastic damping structure;modal loss factor;natural frequency

TB153

A

1000-1093(2016)01-0155-10

2015-05-08

国家自然科学基金项目(51305288、51405323);山西省青年科学基金项目(2013021020-1)

孙宝(1981—),男,讲师,博士研究生。E-mail:bao810321@163.com;孙大刚(1955—),男,教授,博士生导师。E-mail:793456439@qq.com