空投货台摆荡阶段流体-固体耦合建模分析

汤健华,钱林方,徐亚栋

(南京理工大学机械工程学院,江苏南京210094)

空投货台摆荡阶段流体-固体耦合建模分析

汤健华,钱林方,徐亚栋

(南京理工大学机械工程学院,江苏南京210094)

为获得空投货台摆荡阶段的精确动力学响应,考虑货台大幅度摆荡对空气产生的非定常效应,基于平衡点法构建了空投吊挂系统多体动力学模型,并采用基于ALE格式的有限体积法建立了空气流场模型,在此基础上推导建立了非定常流动作用下的货台-空气流体-固体耦合分析模型。通过数值算例研究:验证了该多体动力学模型的鲁棒性和正确性;明确了层流非定常模型能较好地描述流体对平板的作用力,可用于空投货台摆荡阶段的流场分析;对比指出通过流体-固体耦合分析得到的非定常流动气动力显示出震荡特性,而定常流动假设模型会给货台带来类似粘滞阻尼的特性,其减速效果要比非定常流动模型强烈。

流体力学;非定常流动;平衡点法;空投货台;流体-固体耦合

DOI:10.3969/j.issn.1000-1093.2016.01.021

0 引言

当空投货台从机舱拉出以后,空投货台在自身重力、初速度作用下进行落体运动,同时降落伞随着货台及牵引伞的作用拉出伞包并开始充气,空气对降落伞的气动阻力通过吊挂连接绳索传递到货台上,使货台瞬时减速,并在空中进行大范围的摆荡,其结构示意图如图1所示。在周围空气的作用下,货台动能以加速货台周围空气运动的形式耗散,最终货台平稳下降。这个过程称为空投系统的摆荡阶段,在此期间伴随有强烈的空气流动,货台经历大幅度的位移、翻转和速度突变,可能对空投物资产生损害。因此,建立精确的数学模型预测货台在摆荡阶段的响应,对于空投系统的改进、优化具有实际的工程意义。

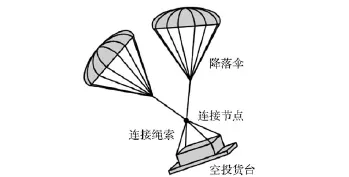
图1 空投货台及吊挂结构示意图Fig.1 Schematic diagram of Airdrop sling system

研究货台在摆荡阶段的响应,关键问题在于构建精确的空气对货台的气动力模型[1-2]。早期研究工作主要通过试验或数值的方法获得货台在定常流动下的气动力系数。Kenneth[3]通过试验的方法测定了定常流动下钝体平板的升阻力系数与迎角的关系,并罗列出了影响流场及升力的因素[4]。Mcquilling等[4]使用计算流体力学方法,计算了定常流动下货台在不同迎角所受的升力和阻力,并与试验结果对比吻合较好。然而,基于定常流动的气动力模型与货台摆荡阶段的实际情况有较大的差别。文献[2]进行空投货台试验发现,采用定常流动的气动力模型作为驱动,计算得到的货台响应与试验有明显区别。表现为,当货台仍然做较大范围的摆荡运动时,仿真计算的结果已经趋于稳定。Kenneth[3,5]通过试验研究了刚性平板在液体中的升阻力,指出定常流动下得到的升阻力系数与非定常流动下得到的测量结果相差较大。货台在摆荡过程中迫使周围的空气运动改变空气流场分布,呈现出明显的非定常流动特性,因此应基于非定常流动理论建立气动力模型。

货台因为摆荡运动改变了周围流场的分布,同时也受到气动力的驱动作用,运动姿态发生调整,二者之间相互耦合作用。为了获得货台摆荡阶段精确的动态响应,必须要建立多体动力学和流场计算相耦合的分析模型。然而由于问题的复杂性,关于货台的流固耦合分析模型,尤其是非定常流体-货台耦合模型的研究鲜见报道。

本文基于平衡点法和ALE格式有限体积法推导建立了考虑非定常流动作用的货台-空气流体-固体耦合分析模型。首先,推导基于平衡点法的Newton-Raphson统一迭代格式,得到能够精确捕捉吊挂松弛-张紧的货台多体动力学计算模型。然后,对时间域进行离散,在每一个时间步内通过建立的多体模型获得货台位置响应,更新货台流体位置界面。通过基于ALE格式有限体积法求解经过界面更新的流场,得到空气流体作用力。将获得的气动力参数作为下一时间步多体模型的输入载荷。最后,通过算例验证说明了考虑非定常流动作用的耦合模型与采用定常流动气动力模型的区别。

1 货台多体动力学分析

1.1 货台动力学问题描述

吊挂结构是空投系统最常用的一种结构。典型的吊挂结构通过数根连接绳索把货台与承载结构(如降落伞等)连接起来,这种结构在工程中已有广泛的应用[6-7]。在摆荡过程中,货台由于自身惯性,其头部或尾部翘起。使吊挂结构中的吊带经历松弛-绷紧-松弛的交替状态,如图2所示。

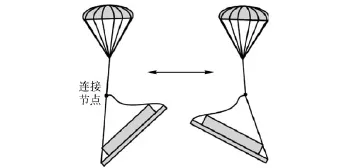
图2 货台在空中摆荡时绳索的松弛Fig.2 Slackness of sling lines

当绳索两连接点间的距离小于绳索的原始长度时,绳索刚度为0.相反地,当绳索两连接点间的距离大于绳索的原始长度时,绳索近似服从胡克定律,其材料特性如图3所示。张力-应变可以通过分段函数表示[8-9],如 (1)式所示。

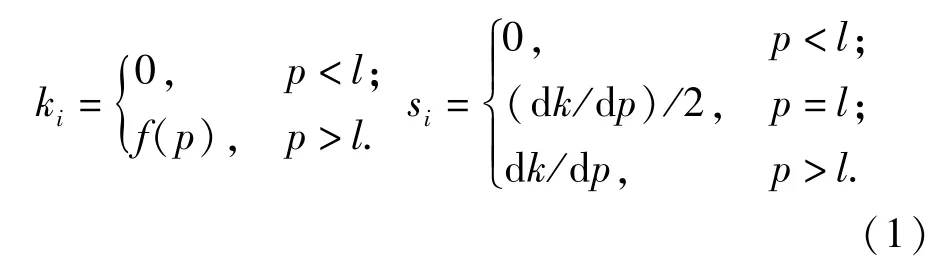
式中:l是加载前未变形的原始长度;p是绳索变形后的长度;s是绳索刚度的斜率,很明显,绳索的刚度斜率不满足1阶连续性。

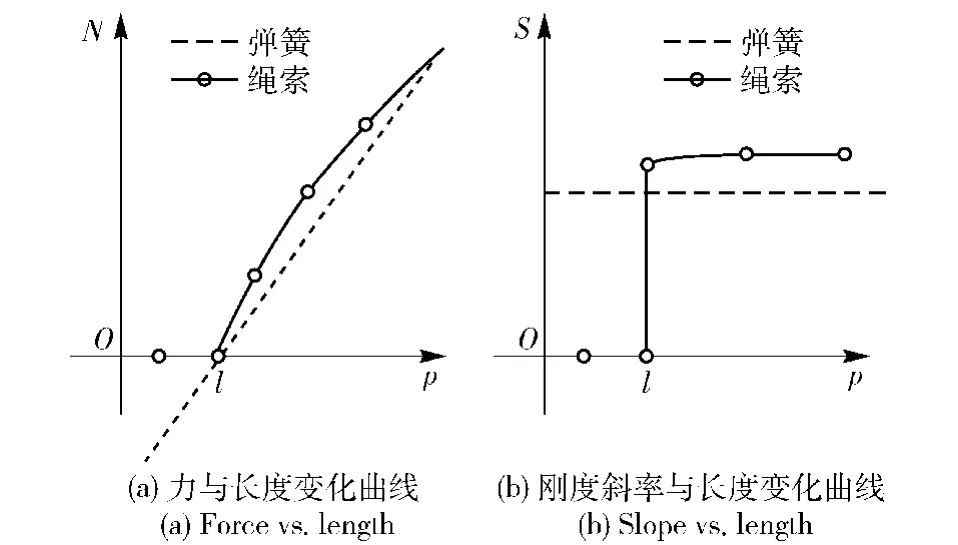
图3 绳索的材料特性Fig.3 Constitutive relations of sling lines

由于绳索只能传递力而不能承受弯矩,因此,把连接节点考虑为质点,不考虑连接节点的转动对绳索的影响。通过这一假设,多体动力学运动方程可以描述为

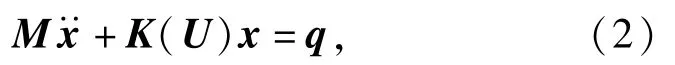
式中:M是质量矩阵;K是刚度矩阵;U是绳索节点的位置向量;x是广义位移向量。由于绳索是典型的非线性材料,且刚度斜率不满足1阶连续性,使得吊挂系统的微分方程组具有较大的刚性,迭代求解时有可能在根附近来回震荡。采用平衡点法可以有效的解决这个问题,使吊挂系统的多体动力学模型更加鲁棒稳定。

1.2 平衡点法统一迭代格式

平衡点法最早由Poole提出并用于求解刚性方程组[10],经过文献[11-13]的发展,已经证实能够应用于多根绳索的模型以及吊挂系统计算中。平衡点法就是通过求解连接节点的力平衡方程组得到连接节点的位移,本文采用Newton-Raphson方法推导建立了基于平衡点法的统一迭代格式。

忽略连接节点自由度,多体动力学运动方程变为

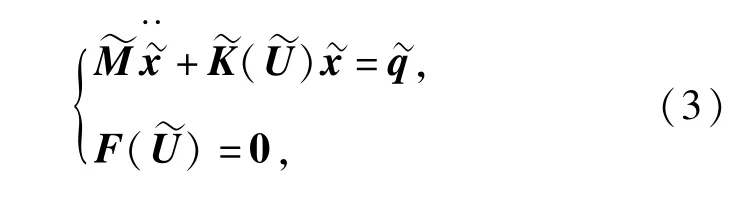
1)固定连接节点的位置,求解其他部件的的响应。

2)固定其他的部件,反复迭代求出连接节点的位置,直到收敛。

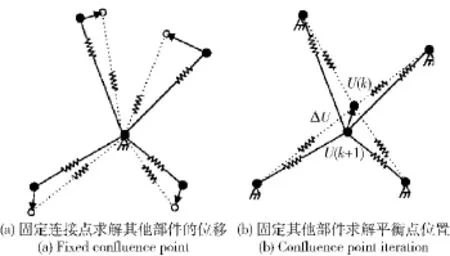
图4 寻找连接点坐标的迭代过程Fig.4 Iteration process of connective nodes

不失一般性,如(3)式所示,可以得到在连接点处的合力为

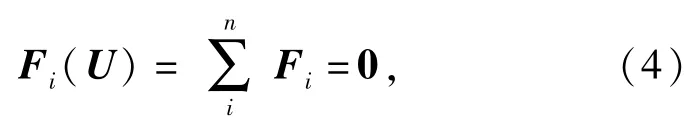
式中:Fi是第i根绳索的阻力。

为了能够得到数值求解连接点的坐标信息,这里使用牛顿方法进行迭代,迭代的过程表示为

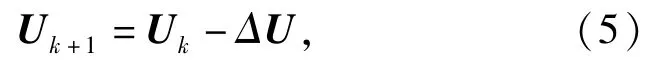
式中:变化的位移为

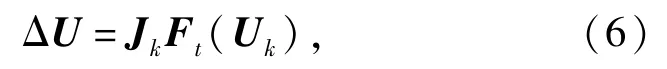
Jk是第k个Newton迭代步的雅克比矩阵。对于三维情况而言,矩阵求解规模为3阶。

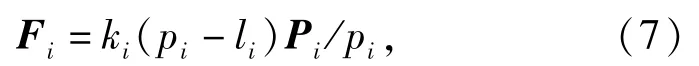
式中:Pi是连接点到绳索另一端的向量;pi是该向量的模;ki是绳索的弹性模量;li是没有加载变形前绳索的原始长度。对该式的弹性力向量求微分得到

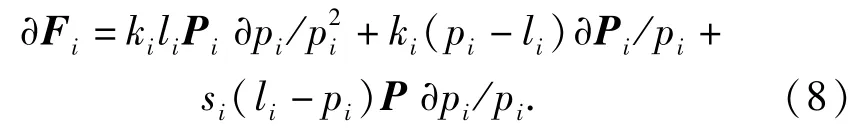
由关系式

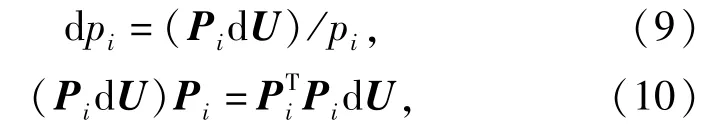
可以得到如下关系:

第i根绳索的雅克比矩阵可以修改为

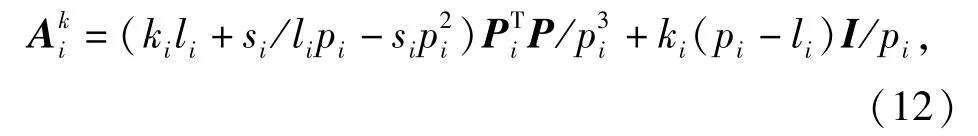
式中:I为单位矩阵。吊挂关于连接节点的雅克比矩阵为

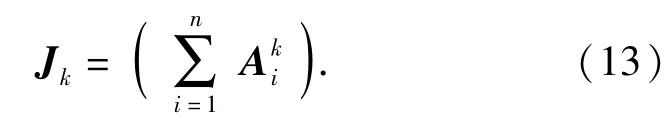
考虑到绳索的刚度可能为0,在迭代的过程中,有可能只有两个或单个绳索受力,导致奇异,如图5所示。对雅克比矩阵J的行列式进行判断,当行列式小于容差时,需要对雅克比矩阵J进行满秩分解:

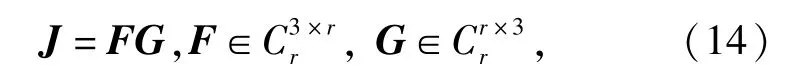
式中:r为张紧绳索的条数。使用广义逆公式,得到雅克比矩阵的广义逆来替代雅克比矩阵的逆:

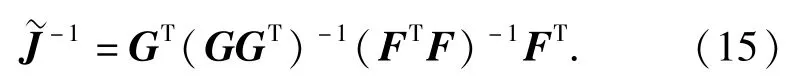
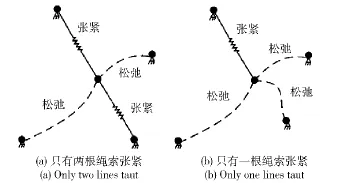
图5 可能导致奇异的情形Fig.5 Singularity phenomenon

因为连接点的维数限制,迭代矩阵的规模为3阶,大大降低了求解的难度,提高求解效率。而且对时间步长也没有了稳定性限制。

2 非定常空投货台流体-固体耦合分析

为了考察货台大幅度摆荡对空气产生的非定常效应,需要考虑随时间不断变化的货台对周围空气流场分布的影响。本文通过基于ALE格式的有限体积法对货台周围空气流场分布进行求解,流体质量方程和动量方程为

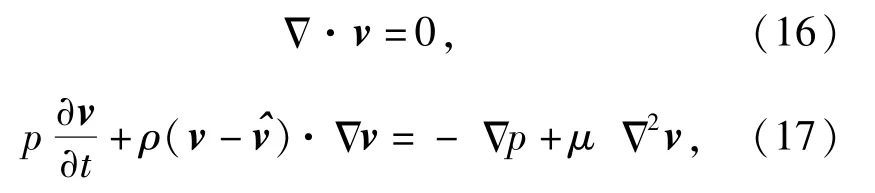
应当注意的是,基于定常假设的流体-固体耦合模型通过货台角度与气动力系数计算作用在货台上的气动力。因此需要额外获取定常气动力系数以及力矩系数随角度变化关系。而采用上述流体-固体耦合分析方法由于已经通过求解NS方程获得作用在货台上的升阻力及作用在货台上的力矩,不需要额外获取气动力系数。

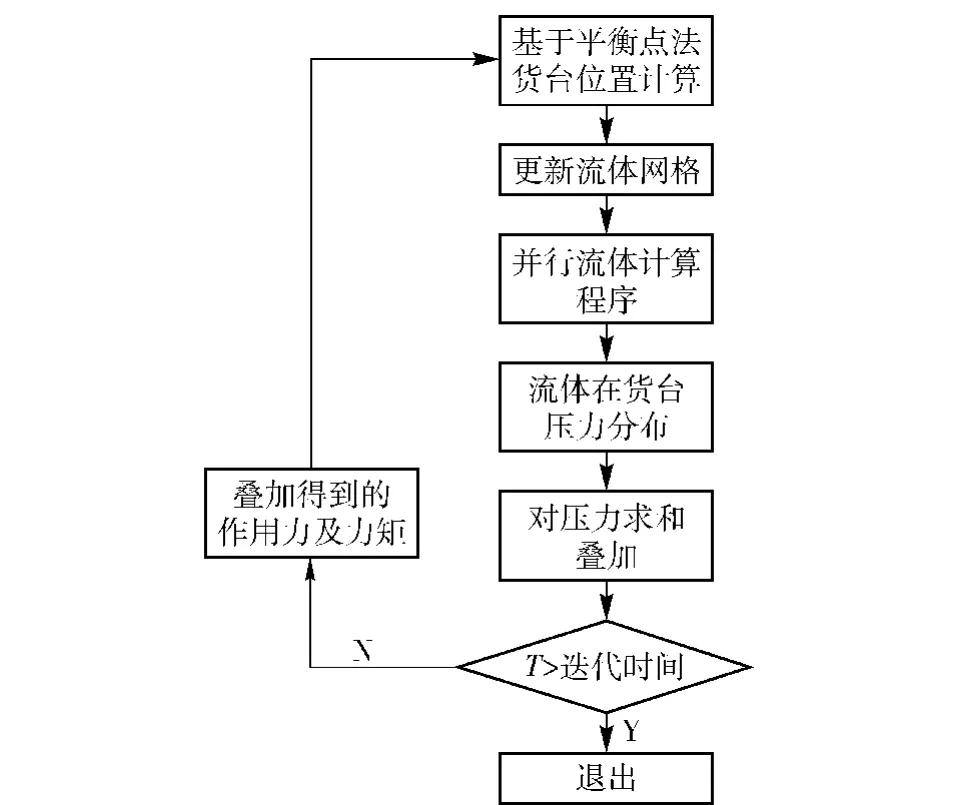
图6 流体-固体耦合分析过程Fig.6 Flow chart of FSI Process

3 算例

3.1 平衡点法分析

为了验证所建立动力学模型的正确性,本文计算了货台在真空中的响应。将降落伞的连接点固定,建立的模型如图7所示,将计算结果与商业多体动力学程序RECURDYN结果进行对比。

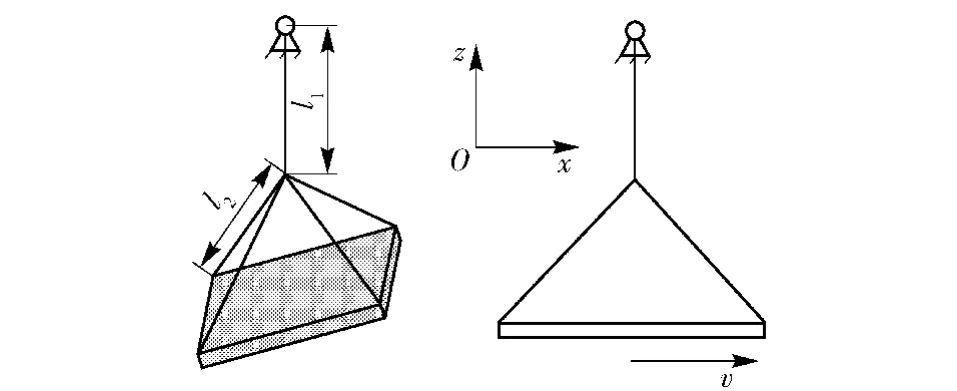
图7 货台的初始状态Fig.7 Initial state of platform

验证的模型参数为:平板的尺寸为4.864 1 m× 2.0574 m×0.101 6 m,绳索连接于平板的4个角,4根连接绳索的原始长度为l1=4.750 71 m.初始速度幅值为5 m/s,方向沿着χ轴正方向,连接节点与固定点绳索的原始长度 l2=2 m.惯性矩阵为104IKg·m2,绳索的本构关系为

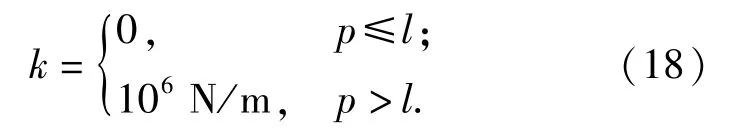
通过控制较小的积分步长得到精确的解,RECURDYN程序的最大时间步长取10-6s,平衡点法的时间步长取为10-3s.分别计算了连接点位移,平板速度与角速度,如图8～图10所示,对比显示两者计算结果一致。说明基于平衡点方法建立的多体动力学模型能够在较大的时间步长下准确地描述货台吊挂结构的响应,具有良好的鲁棒性。

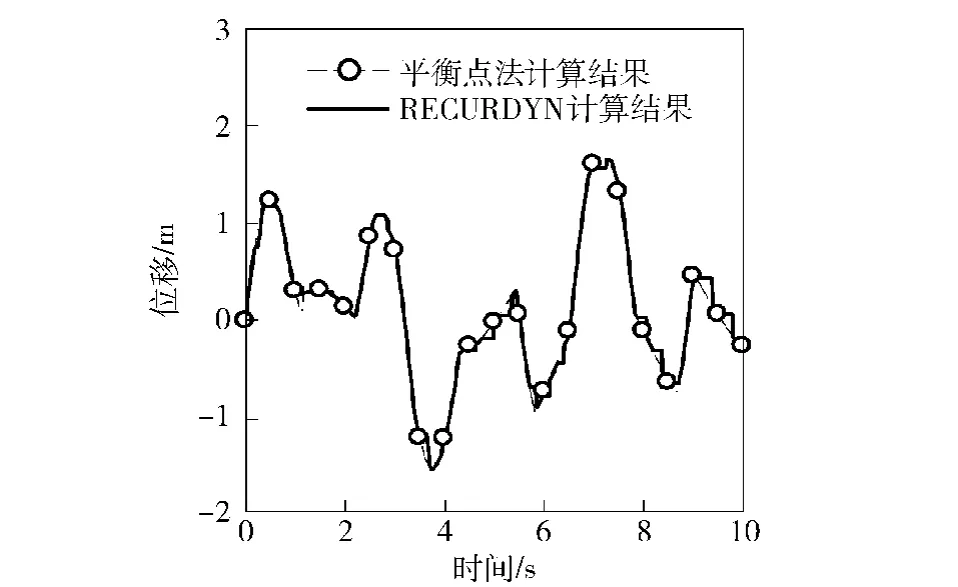
图8 连接节点χ位置随时间变化Fig.8 Positon of connective node vs.time in direction χ

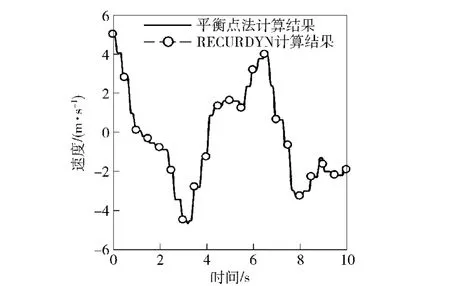
图9 χ方向速度随时间变化曲线Fig.9 Velocity of platform vs.time in direction χ

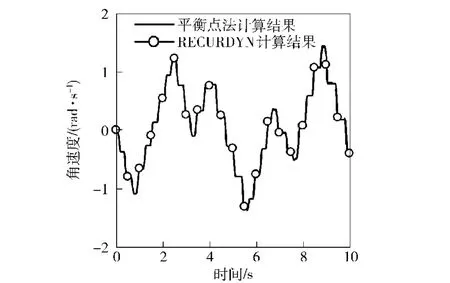
图10 角速度随时间变化曲线Fig.10 Angular velocity vs.time

3.2 非定常流动模型对气动力的影响

Kenneth[5]曾经通过试验手段(见图 11和图12)获得定常流动与非定常流动的升阻力系数,并指出定常流动下得到的升阻力系数与非定常流动下得到的测量结果相差较大。试验的结构如图11所示。

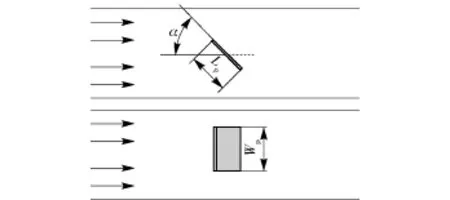
图11 平板的主视图与俯视图Fig.11 Front and vertical views of plate

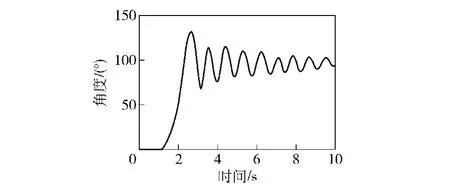
图12 平板角度α随时间变化曲线Fig.12 Angle α vs.time

在水槽中的平板与水槽来流方向成角度α,使用的流体是水,来流速度为0.2 m/s,雷诺数为3.8×104.试验的具体尺寸参数如表1所示。

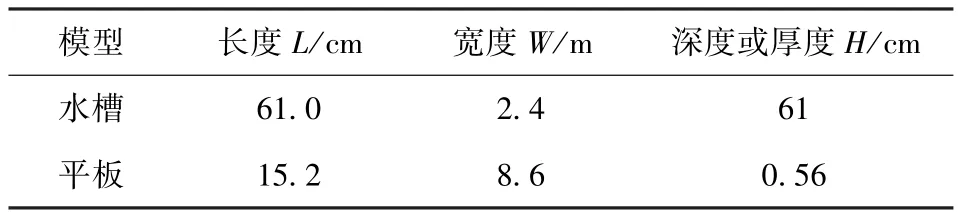
表1 定常模型尺寸参数Tab.1 Sizes of water tunnel and plate

Kenneth[5]通过固定平板攻角,待来流趋于稳定情况下测量流体对平板的作用力,获得定常流动下平板的升阻力与角度α的关系,通过(19)式进一步得到升阻力系数与角度α的关系。

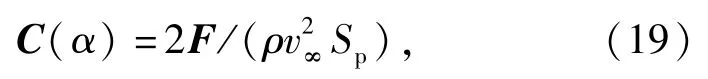
式中:C为升阻力系数向量;F为平板所受的力向量;v∞为来流速度;Sp为货台的面积。

本文通过求解定常N-S方程得到升阻力系数随角度的变化关系,并与试验测量数据进行对比,如图13、图14所示。从对比结果可以看到,虽然最大阻力系数与试验结果有一定误差,但是变化趋势与试验结果吻合较好。

Kenneth[5]通过驱动平板按预定规律运动,攻角α随时间的变化关系如图12所示,实时测量流场对平板的作用力,获得非定常流动下的升阻力系数(如图15～图18中的实验数据)。在已知平板运动规律(图12所示)和升阻力系数与攻角关系(图13和图14)的前提下,确定对应时刻平板的攻角值,并对该攻角值所对应的升阻力系数进行插值,就可以近似得到定常流动假设下升阻力系数的时间历程。图15和图16对比了基于定常流动假设计算的升阻力系数与试验测量结果,由于通过定常流动计算得到的升阻力系数并没有充分考虑平板运动对流场的影响,因此与试验结果有较大差别。

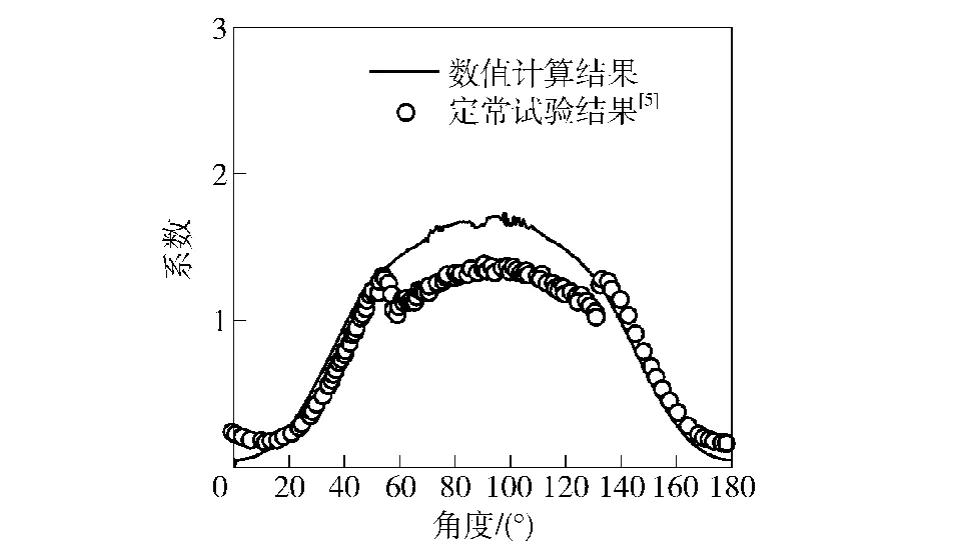
图13 定常阻力系数随角度变化曲线Fig.13 Steady drag coefficient vs.α

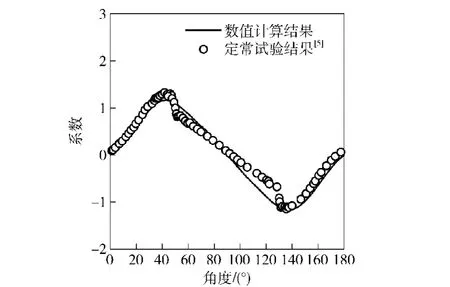
图14 定常升力系数随角度变化曲线Fig.14 Steady lift coefficient vs.α

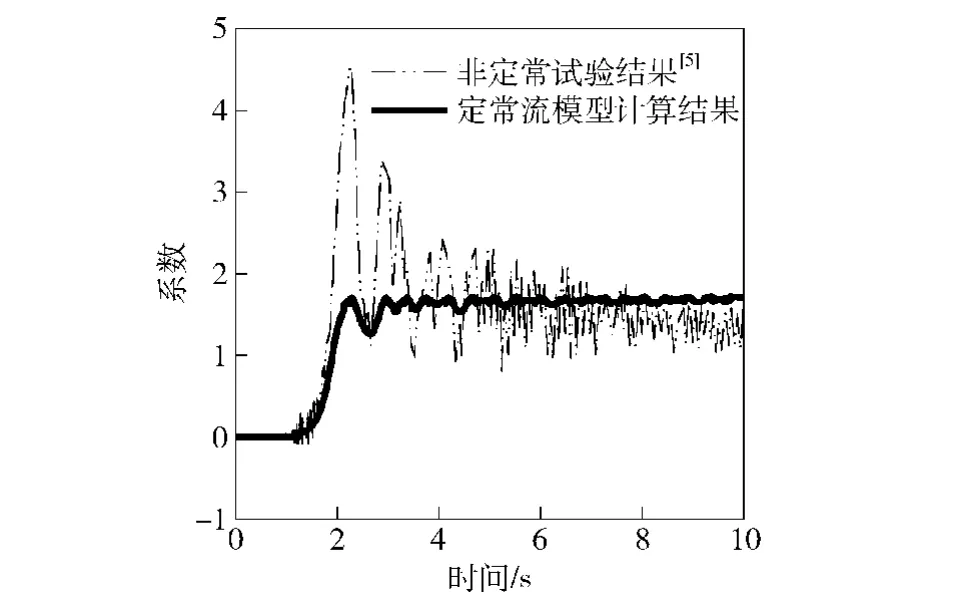
图15 插值得到的阻力系数时间历程Fig.15 Time history of interpolated steady flow drag coefficient

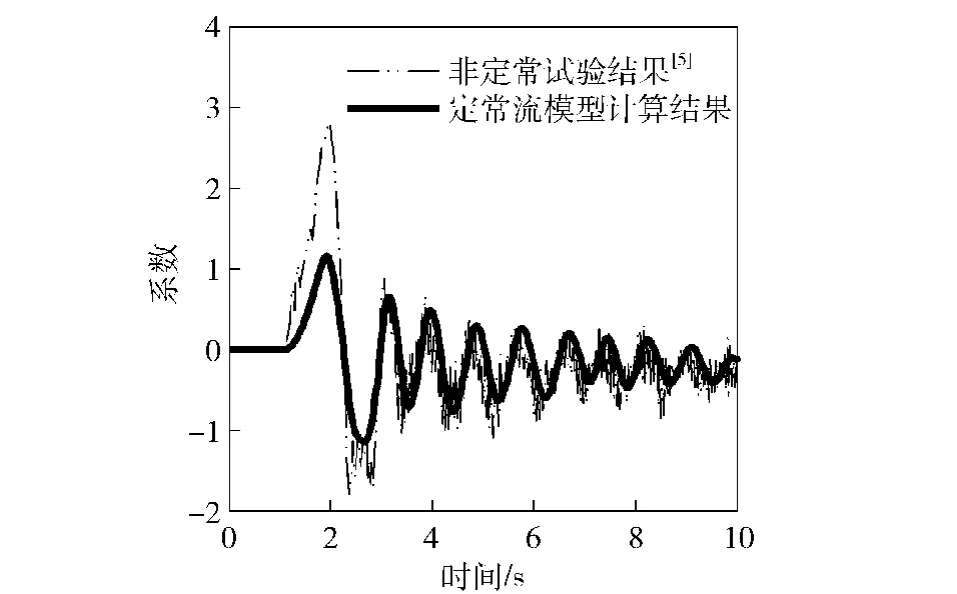
图16 插值得到的升力系数时间历程Fig.16 Time history of interpolated steady flow lift efficient

考虑到固体运动与流场之间的相互耦合作用,非定常流动模型更加符合实际情况。采用本文提出的非定常流固耦合分析方法,平板运动参数预先设定,平板转动会导致周围流场改变,气动力也发生相应的变化。基于非定常流动模型的升阻力系数计算结果如图17和图18所示,可以看到计算结果与试验结果吻合较好。因此可以相信,在低雷诺数流动中,使用层流非定常模型能比较好地获得空气对平板的作用力。

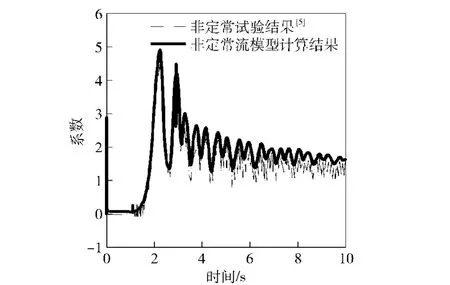
图17 考虑平板运动的非定常阻力系数时间历程Fig.17 Time history drag coefficient of moving plate

3.3 流体-固体耦合算例分析

本算例旨在模拟货台在空气中自由摆荡,观察气动力对货台的影响,吊挂结构和货台参数与3.1节算例相同,空气来流速度为0.1 m/s沿着z方向。为了保证货台在有效流场网格范围内运动,构建的流场尺寸为36 m×36 m×36 m,划分的网格数目为499 381个,时间历程为10 s.在本算例中,多体力学方程通过编写基于平衡点法的多体力学程序进行求解。流体求解通过商业CFD求解器FLUENT进行。编写的多体程序以用户自定义函数(UDF)的形式经FLUENT调用,使用联想服务器(Think Station D30),通过30线程并行计算,计算时间约为48 h.

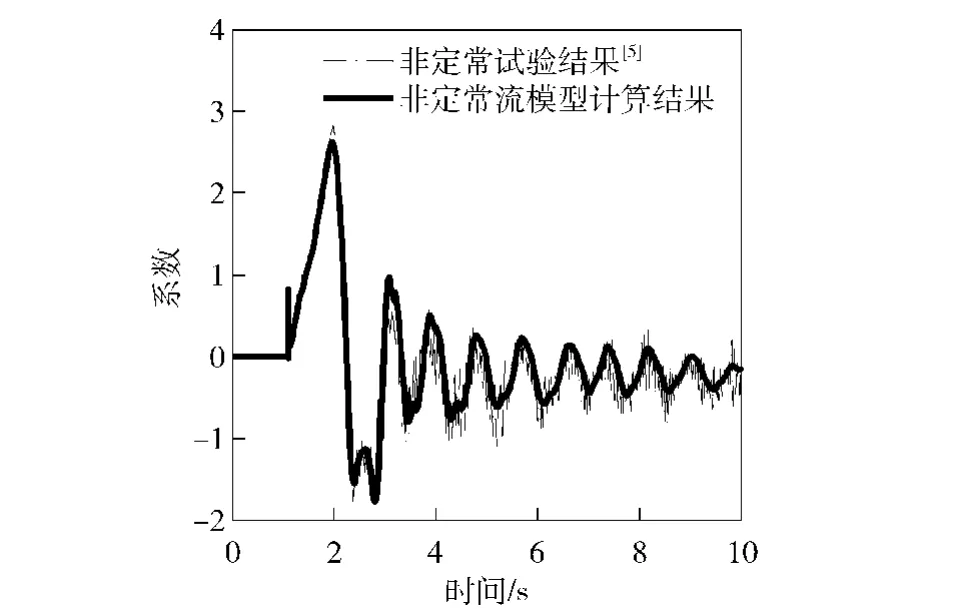
图18 考虑平板运动的非定常升力系数时间历程Fig.18 Time history of lift coefficient of moving plate

截取货台对称平面 Oχz平面(如图20所示),直观展示货台的气动力分布,货台在Oχz平面的压力分布随时间变化关系如图19所示,在半个摆荡周期内货台上下表面的压力分布不断交替,货台χ方向气动力合力随时间变化曲线如图21所示。由于定常流模型下气动力仅是攻角的函数,而考虑非定常流模型后气动力除了与货台的攻角有关,还与上一时刻流场参数和当前货台的运动状态有关,需要考虑固体和流体之间的耦合作用逐步计算获得。因此,在图21中,通过非定常流动计算的气动力变化剧烈,而通过定常流动升阻力系数预测的气动力却只有较少的震荡,整个气动力曲线显得光滑规整。对比显示出,非定常流动模型下得到的气动力小于定常流动模型的计算值,二者在多体系统中都起到粘滞阻力的作用。

货台在摆荡过程中除了气动力的影响以外,还受到自身重力以及吊挂结构提供的牵引力的影响。由于货台重量及惯量相对较大,货台在自身重力、惯性力及牵引力作用下来回摆荡,而气动力则主要起到阻尼作用。为了考察耦合作用下空气对货台的耗能效果,观察采用不同的流动模型得到的货台速度幅值变化情况籍此了解能量的衰减,对比结果如图22所示。在货台摆荡过程中,定常流动模型与非定常流动模型都展示了良好的阻尼性质,两种模型下系统的运动规律比较一致,但运动衰减幅度不同,这可以说明在空中摆荡的货台有大部分能量通过加速流体的形式耗散在空气中。其中,定常流动模型显示出较大的阻尼效果,平板速度幅值衰减快于非定常流动模型。这在一定程度上可以解释Peter在货台空投检验试验中的发现[2]:货台仍然做较大范围的摆荡时,通过定常升阻力系数得到的仿真结果已经趋于稳定。

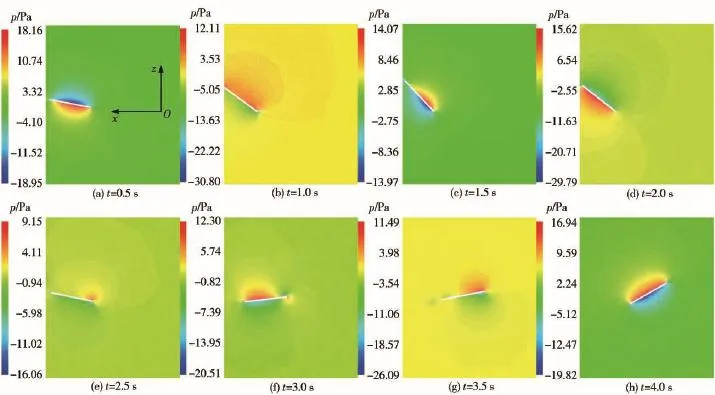
图19 货台在Oχz平面的压力分布Fig.19 Pressure distribution of platform on Oχz plane

图20 货台的运动平面Fig.20 Oχz plane of moving platform

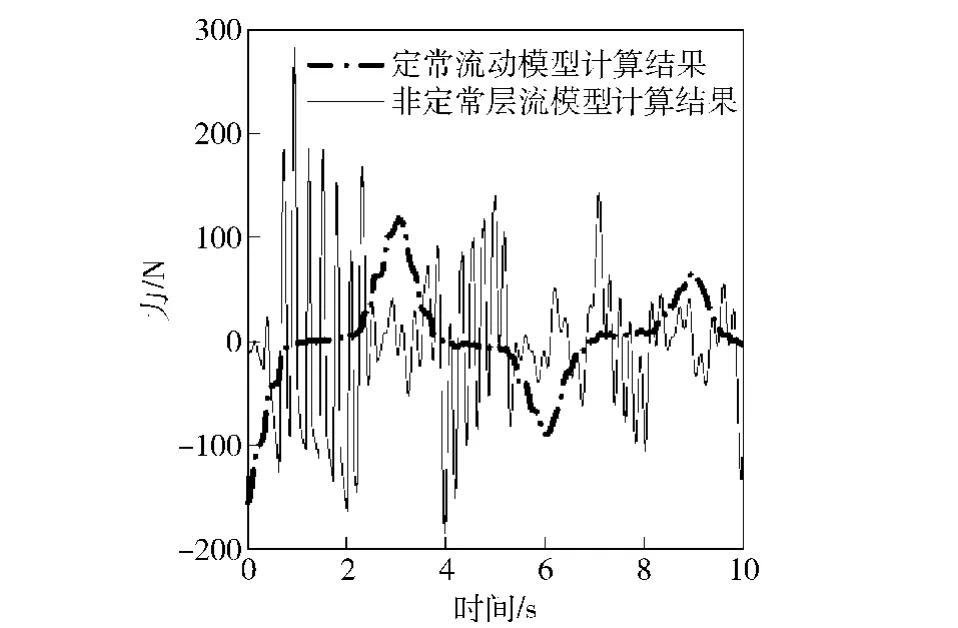
图21 χ方向气动力时间历程Fig.21 Time history of aerodynamic force along χ direction

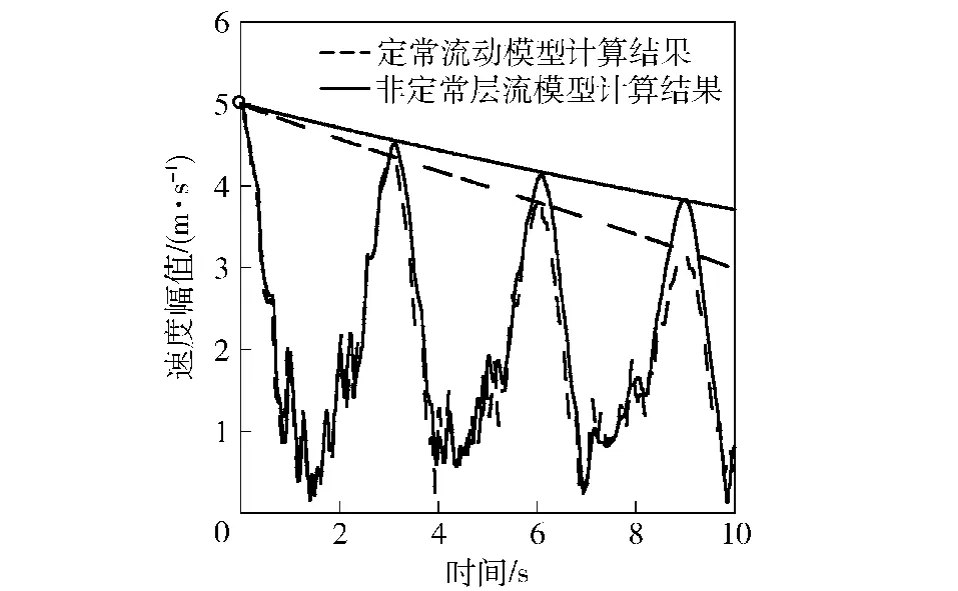
图22 货台速度幅值时间变化曲线Fig.22 Platform velocity amplitude vs.time

4 结论

本文考虑货台大幅度摆荡对空气产生的非定常动效应,基于平衡点法和ALE格式有限体积法推导建立了非定常流动作用下的货台-空气流体-固体耦合分析模型。通过数值算例研究得到了以下的结论:

1)基于平衡点法建立的绳索吊挂系统多体动力学模型具有迭代格式简单、鲁棒性较好的特点,能够精确捕捉连接绳索的松弛-张紧关系。

2)在低雷诺数流动中,使用非定常层流模型能比较好地获得流体对平板的作用力,非定常流动得到的气动力更加符合实际,可作为空投货台摆荡阶段的流场分析方法。

3)通过流体-固体耦合分析得到非定常流动计算的气动力变化剧烈,而通过定常流动升阻力系数计算得到的结果却只有较少的震荡,但其显示出类似粘滞阻尼的特性耗能效果要比非定常模型强烈,这有可能是造成文献中数值分析与试验不相符的原因之一。

References)

[1]Peter C.A software simulation of cargo drop tests[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Monterey,CA:AIAA,2003:2003-2132.

[2]Peter C,Kenneth D.Validation of a cargo airdrop software simulator [C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Monterey,CA:AIAA,2003:2003-2133.

[3]Kenneth D.The motion and aerodynamics of an airdrop platform [C]//22nd Applled Aerodynamics Conference and Exhibit.Provldence,RI:AIAA,2004:2004-4845.

[4]Mcqulling M,Potvin J,Riley J.Simulating the flows about cargo containers used during parachute airdrop operations[J].Journal of Aircraft,2011,48(4):1405-1411.

[5]Kenneth D.Aerodynamic forces on an airdrop platform[C]//18th Aerodynamic Decelerator Systems Technology Conference and Seminar.Munich,GE:AIAA,2005:2005-1634.

[6]Vaughan J,Kim D,Singhose W.Control of tower cranes with double-pendulum payload dynamics[J].IEEE Transactions on Control Systems Technology,2010,18(6):1345-1358.

[7]Masoud Z N,Nayfeh A H,Mook D T.Cargo pendulation reduction of ship-mounted cranes[J].Nonlinear Dynamics,2004,35(3):299-311.

[8]Track H H S T,Holloman N M.Designed experiments for nylon band characterization[C]//US Air Force T&E Days 2010.Nashville,TN:AIAA,2010:2010-1711.

[9]Thomas L,K R.Biaxially oriented nylon-6 as a long duration material[C]//International Technology Conference.Albuquerque,NM:AIAA,1991:1991-3659.

[10]Poole L R,Huckins E K.Evaluation of massless-spring modeling of suspension-line elasticity during the parachute unfurling process,NASA-TN-D-6671[R].WA,US:NASA Langley Research Center,1972.

[11]John F,Robert T,Behzad R.Multibody parachute flight simulations using singular perturbation theory[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Seattle,WA:AIAA,2009:2009-2920.

[12]Raiszadeh B.Mutibody parachute flight simulations for planetary entry trajectories using“equilibrium points"[J].Advances in the Astronautical Sciences,2003,114:913-923.

[13]程文科,秦子增,张晓今.具有倒“Y"型吊挂系统的物伞组合体动力分析[J].弹道学报,1998,10(2):10-14.CHENG Wen-ke,QIN Zi-zeng,ZHANG Xiao-jin.The dynamic analysis of a parachute and payload assembly with an inverted“Y"suspension system[J].Journal of Ballistics,1998,10(2): 10-14.(in Chinese)

Fluid-structure Interaction Modelling of Airdrop Cargo Platform Swinging

TANG Jian-hua,QIAN Lin-fang,XU Ya-dong
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

A platform-sling model is established to study the dynamic response of airdrop platform.An uniform equivalent point Newton-Rapshon iteration method is presented.In order to study the unsteady fluid behavior,the time domain is discretized,and an ALE base finite volume method is used to solve the NS equations.The aero-force is obtained and imposed on the platform.The equivalent point method is validated through commercial software RECURDYN.The results show that the equivalent point method can well represent the slack-taut cases of the sling system.It can also be found that the laminar flow model is used to describe the acting force of fluid on plate well at low Reynolds number.Finally,the comparisons are made between the steady and unsteady FSI models.The time history of unsteady fluid force displays severe oscillation while the steady fluid force varies evenly.

fluid mechanics;unsteady flow;equivalent point;airdrop cargo platform;fluid-structure interaction

TJ011

A

1000-1093(2016)01-0141-08

2015-03-22

国家自然科学基金项目(11472137)

汤健华(1984—),男,博士研究生。E-mail:jian_hua_tang@126.com;钱林方(1961—),男,教授,博士生导师。E-mail:lfqian@vip.163.com