基于Copula函数的数控车床可靠性综合分配方法

杨周,朱云鹏,张义民,任泓睿

(东北大学机械工程与自动化学院,辽宁沈阳110819)

基于Copula函数的数控车床可靠性综合分配方法

杨周,朱云鹏,张义民,任泓睿

(东北大学机械工程与自动化学院,辽宁沈阳110819)

针对串联系统可靠性分配问题,以基于潜在失效模式与后果分析(FMEA)评价指标非线性修正函数的综合分配方法为基础,提出一种考虑故障相关性的综合分配方法。考虑可靠性分配问题中的多因素影响,建立一种考虑因素重要程度的可靠性分配矩阵。针对FMEA评价指标的局限性,分别建立了严重度和失效频率的非线性转换关系,即FMEA修正函数。基于Gumbel Copula函数及Kendall相关系数,建立失效相关系数矩阵,并计算各子系统的相关失效严重度。推导基于Copula函数的串联系统可靠性计算公式,并以此为依据对各子系统的可靠性进行分配。以数控车床主轴系统为例,利用该方法对其进行子系统可靠性分配,阐述了该方法的特点及适用性。对是否考虑故障相关性的分配结果进行比较,认为考虑故障相关性能够为各子系统分配更低的可靠度,从而减小加工及维护成本。

机床技术;串联系统;可靠性;失效模式与后果分析;综合分配;故障相关性

DOI:10.3969/j.issn.1000-1093.2016.01.020

0 引言

机械可靠性分配是根据一定的原则和方法,将整机系统可靠性指标自上而下逐级分配到下属各级产品,最终达到整机系统可靠性指标的过程[1]。机械系统的可靠性在一定程度上取决于设计初期可靠性指标分配过程的合理性。

数控车床(CNC)作为制造业的主要设备,其可靠性程度对制造业的发展起到关键作用[2-4]。由于CNC结构复杂且故障模式繁多,其设计初期的可靠性分配结果常出现不合理或可信度不足的现象,进而影响机床的使用效率及寿命[5]。因此,讨论如何合理地对CNC进行分配或再分配十分重要。

CNC可看作是由多个子系统组成的串联结构系统[6],针对这类系统的可靠性分配问题,学者们做了很多工作。Wang等[7]提出了一种综合可靠性分配方法,列举7种失效及影响因素,通过求解相对失效率,结合专家评分权对CNC进行可靠性分配。Itabashi等[8]根据潜在失效模式与后果分析(FMEA)提出一种考虑严重度和失效频率的可靠性分配方法。Kim等[9]针对传统FMEA分配方法的不足,提出了严重度转换关系的分析方法。Yadav等[10]提出了一种三维分析方法,引入可靠性提成潜力的概念,进行可靠性分配的研究。

在对系统的故障分析中,学者们发现大部分故障并非独立存在的,而是具有一定的相关性。故障相关性对于可靠度的计算和分配均有一定影响,Mou[11]和Huang等[12]分别介绍Copula函数在可靠度计算中的应用,然而其所述的可靠度计算方程形式不尽相同,也缺乏对不同方程间的内在联系的阐述。Chen等[13]基于传统串联系统可靠度分配方法,分析了引入Copula函数后对子系统可靠度分配的影响。

综上所述,目前针对CNC的可靠性分配方法很多,但也存在考虑因素单一或分配方法不合理的问题,对故障相关性的考虑仍有待发展。本文基于Copula函数,结合FMEA非线性转换函数,在考虑故障相关性条件下对CNC进行可靠性分配的研究,并最终通过算例进行验证。

1　Copula函数及其参数估计

1.1 Copula函数与Sklar定理

Copula函数是用来描述变量间相关关系的一个数学工具,是连接变量边缘分布及联合分布的函数。

考虑n个随机变量χ1,χ2,…,χn,设ui=Fi(χi); i=1,2,…,n,Fi(χi)为变量χi的边缘分布函数。则一个n维的Copula函数[14]应满足:

1)C(u1,u2,…,un)为定义在[0,1]n上的n元分布函数;

2)C(u1,u2,…,un)中的每个变量都是单调递增的;

3)对于 C(u1,u2,…,un)的边缘分布函数 Ci满足

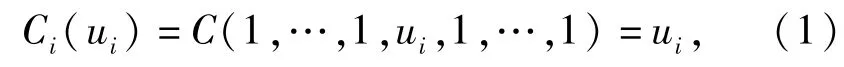
式中:ui∈[0,1],i∈[1,n];

4)对任意ui∈[0,1],i∈[1,n],满足

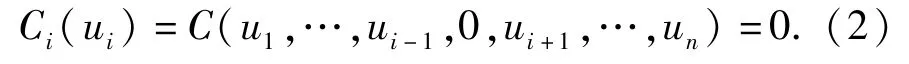
此外,若χ1,χ2,…,χn相互独立,则有C(u1,u2,…,un)[15]:

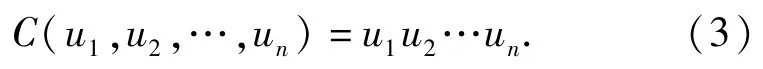
Sklar提出的Sklar定理[15]是Copula函数在统计中应用的基础,它解释了Copula函数在多维分布函数及其一维边缘分布的关系中的作用原理,并给出了构造Copula函数的方法。

设F(χ1,χ2,…,χn)为联合分布函数,则存在唯一的Copula函数C(·)满足:

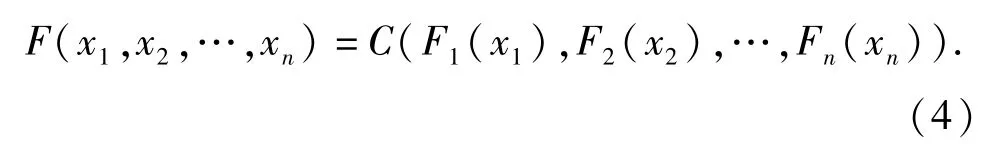
则联合分布的密度函数f(χ1,χ2,…,χn)可写为

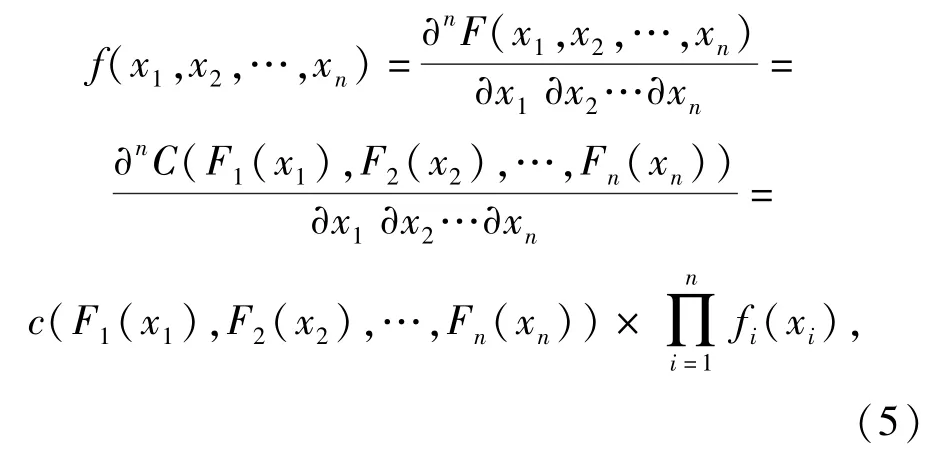
式中:c(·)和fi(·)分别为Copula函数和边缘分布的概率密度函数。

由于ui=Fi(χi),i=1,2,…,n,(4)式可记为

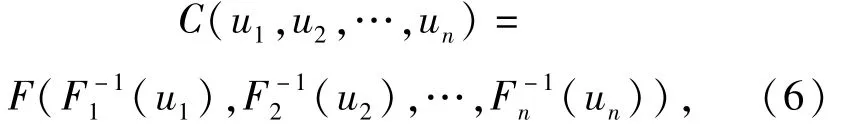
实际应用中的Copula函数种类很多,在机床可靠性分析中,Gumbel Copula函数[14]最为常用:

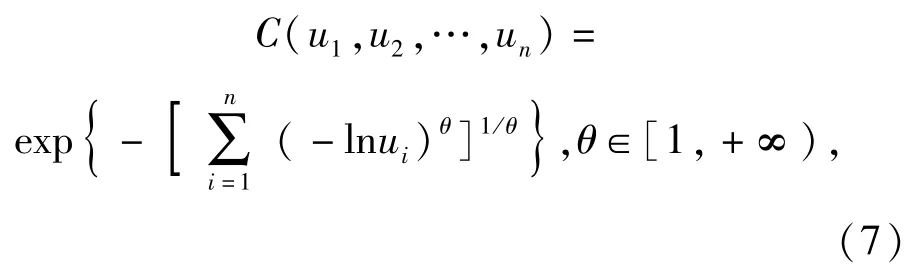
式中:θ为表示变量相关性的参数。

Gumbel Copula函数属于阿基米德Copula函数的一种,文献[16]给出了其分布函数的定义,具体表达式为

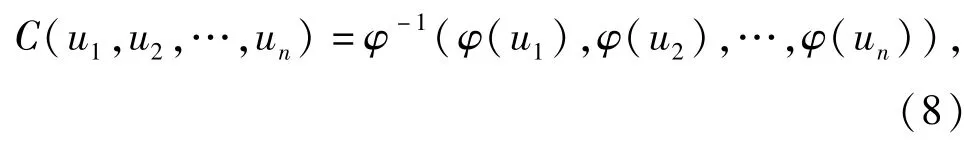
式中:φ(·)称为阿基米德Copula的生成元。

在Gumbel Copula函数中,其生成元为

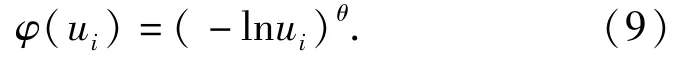
1.2 Copula函数的参数估计

对Copula函数的相关性参数可采用极大似然法进行估计。极大似然法的基本思想是将使样本获得最大概率的参数值作为位置参数的估计值。在Copula函数中,相关性参数θ为未知参数,记随机变量χ1,χ2,…,χn的边缘分布密度函数为f(θ;χi),则样本的联合分布密度函数如(5)式所示,设

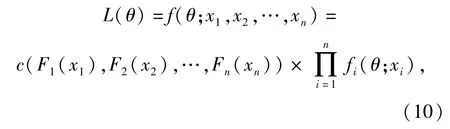
式中:L(θ)为相关性参数θ的似然函数。

根据极大似然估计法,θ的估计值 ^θ应使L(θ)达到最大,即

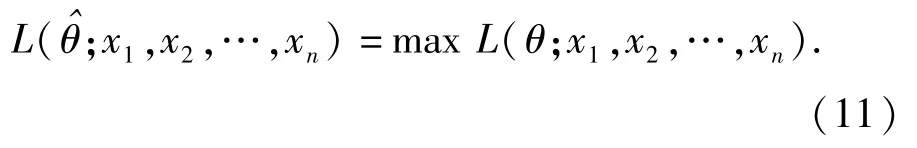
根据(4)式,在已知Copula函数形式的条件下,θ的估计值可通过下式得出:

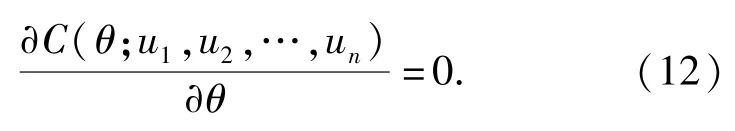
2 基于非线性转换函数的综合分配过程

CNC可视为典型的串联结构系统,在对CNC进行可靠性分配时,除了零部件的失效频率外,还需要考虑失效严重度,维修成本,复杂度等因素。最近,作者基于CNC的FMEA分析,提出了一种考虑非线性转换函数的综合分配方法[17],以解决串联系统多因素的可靠性分配问题。

2.1 多因素综合分配方法

设串联系统U可分为n个子系统,表示为U= {U1,U2,…,Un}.V为系统分配指标,设共有m个可靠性分配指标,表示为V={V1,V2,…,Vm},对于每一个分配指标Vk(1≤k≤m),设其第i个子系统与第 j个子系统的失效率分配相对值,满足:

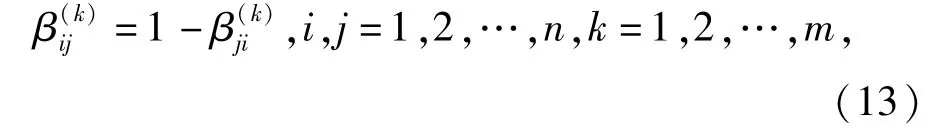
考虑失效率分配相对值矩阵B(k),对于分配指标k可表示为

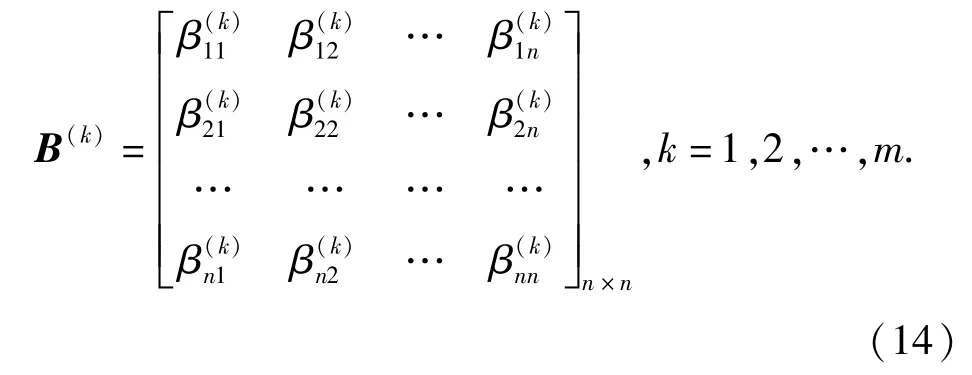
系数矩阵B(k)的每一列代表与该列序号对应的子系统与其它所有子系统的失效率分配相对值。取第i列值的平均数,代表第i个子系统在第k个分配指标下的相对分配系数,写为

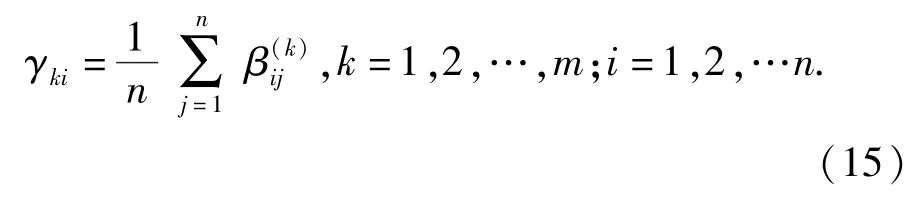
考虑系统共有m个分配指标,根据(13)式,可得到新的分配矩阵Γ:

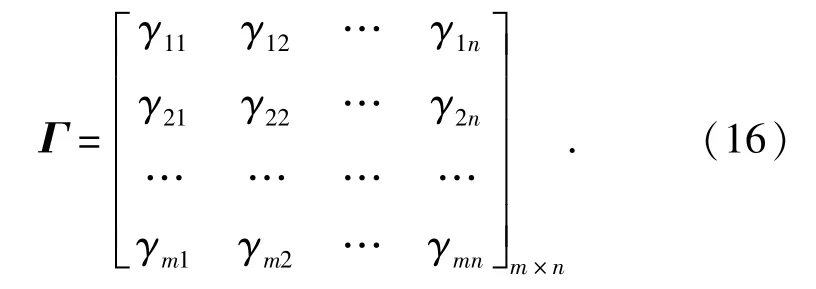
设ai表示子系统i的综合失效率分配系数,定义子系统分配向量A:

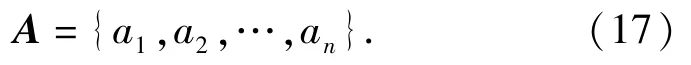
分配向量A可写为

式中:W为权重向量,W={w1,w2,…,wm},其中wk(1≤k≤m)表示第k个分配指标的权重或重要程度。

权重向量W可通过专家打分方法获得,设专家人数为N,则第k个分配指标权重记为

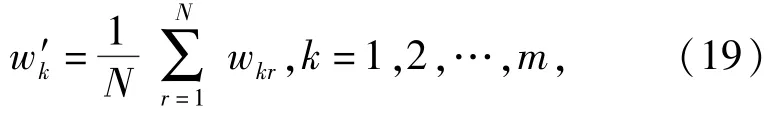
式中:wkr为第r个专家对第k个分配指标的重要程度的评价分数。

则权重向量中的元素可写为

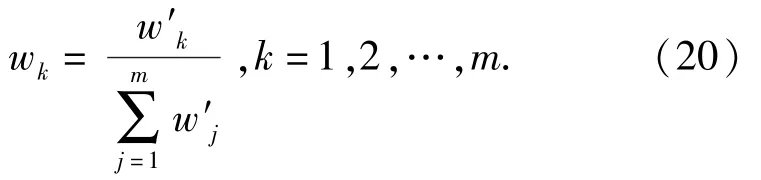
将(20)式与(16)式代入(18)式,可得到子系统失效率的分配向量A,则对于各子系统Ui,i=1,2,…,n,其失效率分配满足:

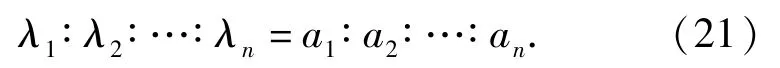
再根据系统可靠度要求即可求得各子系统的可靠度分配结果。

由综合分配方法可知,采用这种方法进行可靠性分配的关键是计算合适的失效率分配相对值为方便后对比故障相关性对可靠性分配结果的影响,根据文献[7],选择6项分配指标,分别为:失效频率(k=1),失效严重度(k=2),复杂度(k=3),加工难度(k=4),工作环境(k=5)和成本(k=6)。各项指标的分配相对值计算方法为:

k=1,3,4,5,6时,分配相对值:

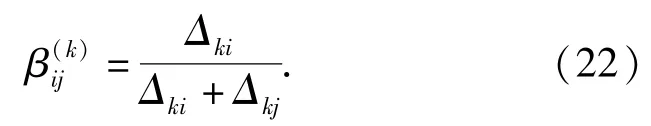
k=2时,分配相对值:

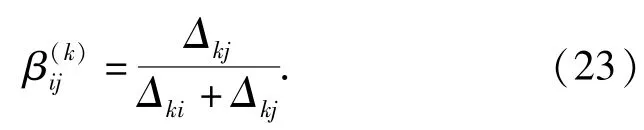
式中:Δki、Δkj分别为在第k个分配指标下子系统i、j的相对失效频率,失效严重度,复杂度,加工难度,工作环境或成本。

(22)式、(23)式表明,对于高失效率,高成本和复杂的子系统,由于其本身的复杂特性,应分配较高的失效率以降低制造和维修成本,而对于高严重度的子系统,则应分配较低的失效率以保证系统的平稳运行。

2.2 FMEA非线性转换函数

文献[9]提出了失效严重度的指数函数转换关系:

然而,(24)式具有一定局限性。设Si=S0和Sj=S0+1,则其相对失效率为

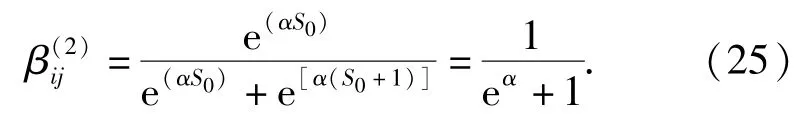
(25)式表明相邻的两个严重度的相对失效率是一样的。

另一方面,失效严重度可分为3个区间,分别为低区间(Si∈[1,3]),中区间(Si∈[4,7])及高区间(Si∈[8,10]).考虑失效严重度集中在低区间及中区间的情况,指数转换方程则不再适用,它不能反应低失效率的影响。这是因为指数转换方程的导数为

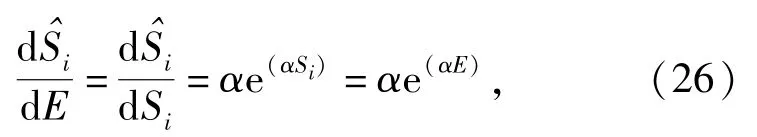
式中:E为FMEA严重度水平;Si=E.

在(26)式中,随着严重程度增加,Si的值增加逐渐加快。事实上,在均匀分配状态下,高严重度的增加速度应适当减小。需要注意的是,持续增长的趋势只在严重度集中在高区间情况下适用。

针对指数函数转换关系的局限性,提出一种3阶转换的设计方法。以失效严重度为例,考虑2阶方程:

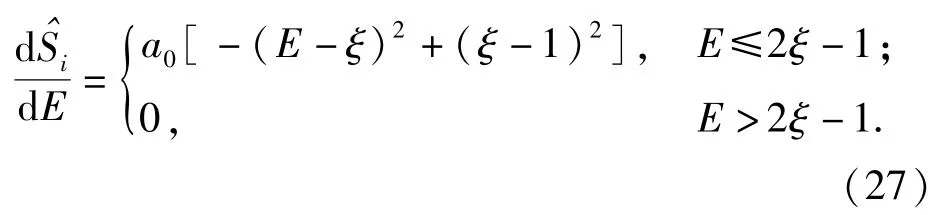
式中:E为FMEA失效严重度水平,E∈[1,10]; a0为实常数;ξ失效严重度集中水平为待定转换函数。

根据(27)式,可得到3阶转换方程:

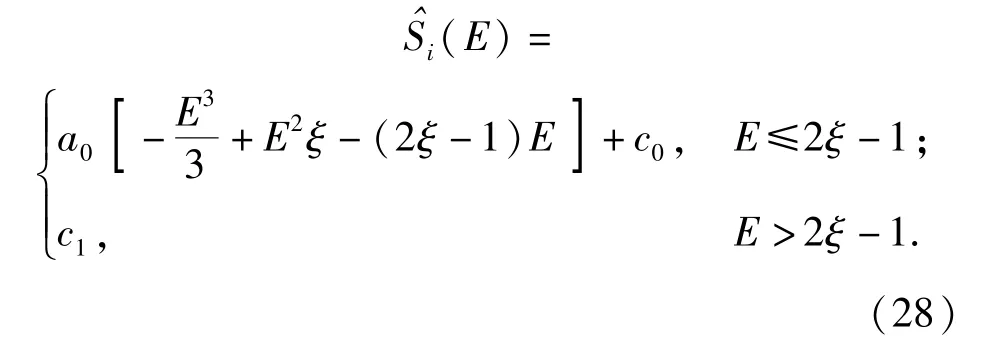
式中:a0、c0和c1均为待定系数。

定义条件方程:

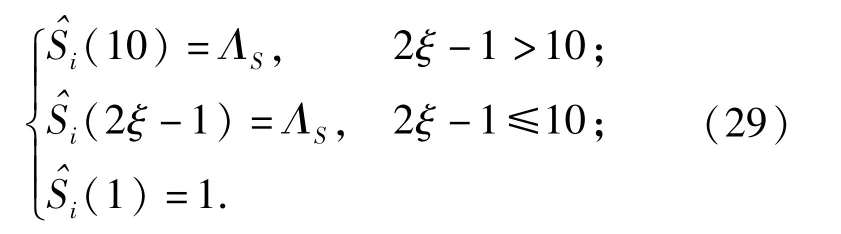
则a0、c0和c1可通过将(29)式代入(28)式得到。在(28)式、(29)式中,ΛS可根据要求人为确定。

图1描述为ΛS=10时的3阶转换函数和α= 0.23时的指数转换函数。

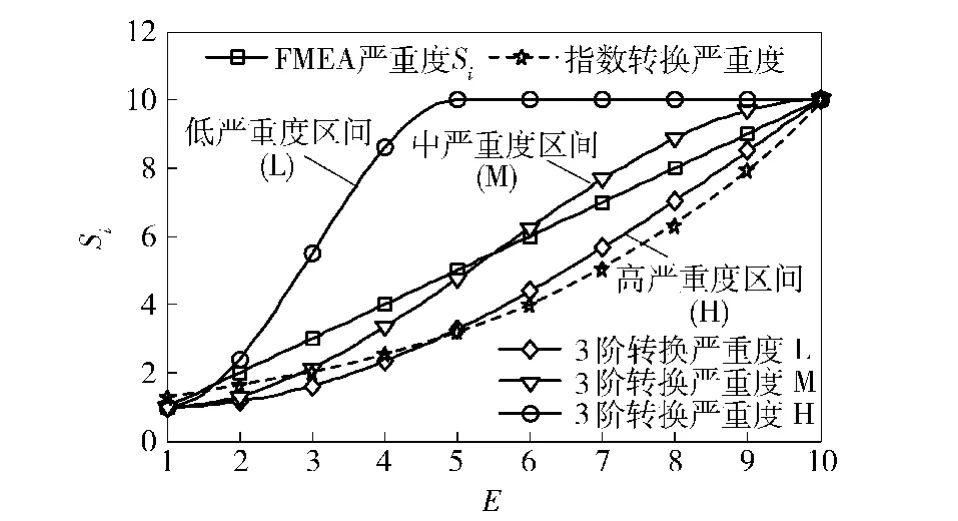
图1 3阶转换函数及指数转换函数曲线Fig.1 Curves of three order transfer function and the exponential transfer function

在图1中,可以看到当ξ集中在高严重度区间(H)时,3阶转换函数与指数转换数具有相似的性质,可以相互替换。然而,当ξ在低(L)、中(M)严重度区间时,高区间转换严重度基本不变或变化很小。这是合理的,因为如果平均严重度在低、中区间内,其严重度在高区间内的情况非常少,不应作为关注的重点。实际上,严重度完全在低区间内的情况在实际中是很少见的。因此,相对严重度可重新表示为

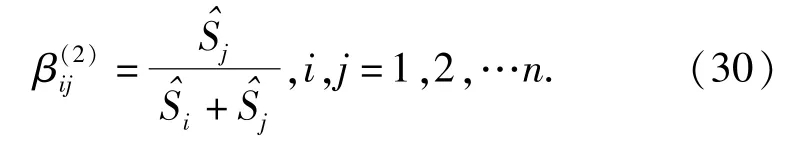
3 考虑故障相关度的可靠性综合分配方法

由于通常情况下,数控机床各子系统的故障并不是独立存在的,某一个子系统的故障会导致其它子系统故障的发生,因此,需要在可靠性分配时考虑个子系统间的相互影响,考虑子系统的相关失效严重度指标(k=7),即某一子系统对其它子系统的影响程度:

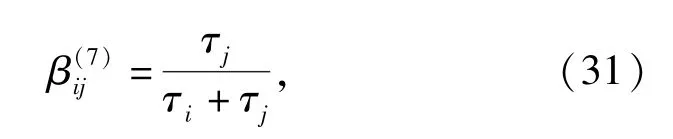
式中:τi、τj分别为子系统i、j的相关失效严重度。

3.1 Kendall相关系数

设从样本中选取的两组观测值(X1,Y1)和(X2,Y2)为独立同分布的随机向量,定义Kendall相关系数[16]为

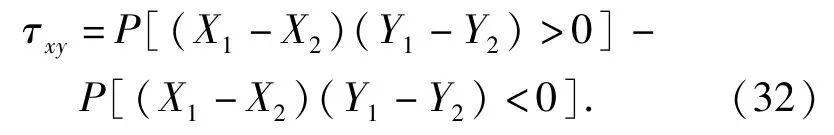
式中:(X1-X2)(Y1-Y2)＞0表示X和Y变化趋势一致;(X1-X2)(Y1-Y2)＜0表示X和Y变化趋势不一致。

若X1、X2的边缘分布函数均为u=Fχ(·),Y1、Y2的边缘分布函数均为v=Fy(·),则(X1,Y1)和(X2,Y2)的 Copula函数可分别记为 C1(u,v)和C2(u,v),二者的Kendall相关系数为

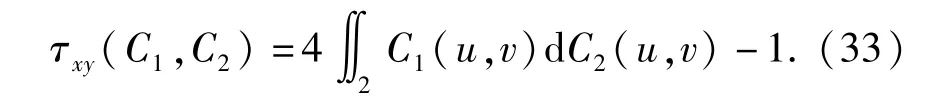
进一步可知,若X、Y是具有Copula函数C(·)的连续变量,则X、Y的Kendall相关系数为

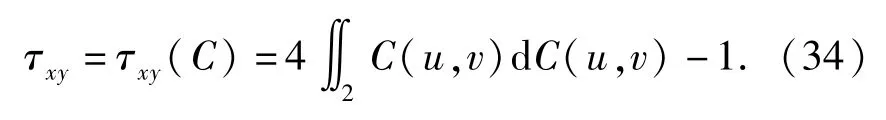
考虑两变量的Gumbel Copula函数,将(7)式代入(34)式,得

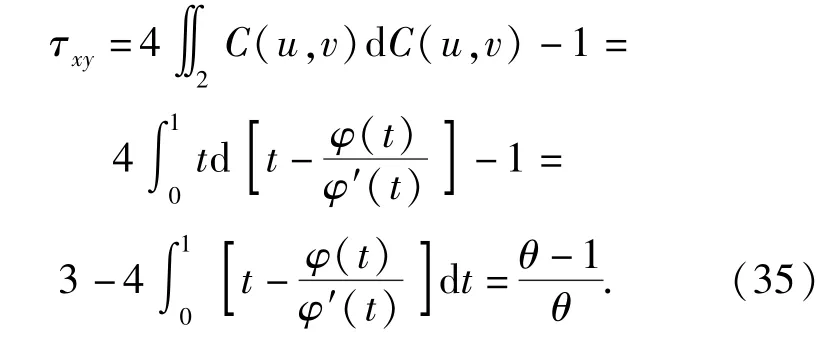
对于由n个子系统组成的系统,各子系统发生故障的随机变量表示为X={X1,X2,…,Xn},则第i个子系统和第j个子系统的故障相关系数可记为τij,i,j=1,2,…,n,子系统相关性矩阵可表示为

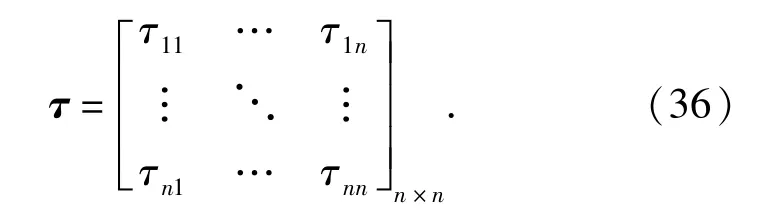
3.2 故障相关度对系统可靠性的影响

一个机械系统中,若第i个子系统的寿命为Xi,则其失效概率为Fi(t)=P{Xi≤t},可靠度为

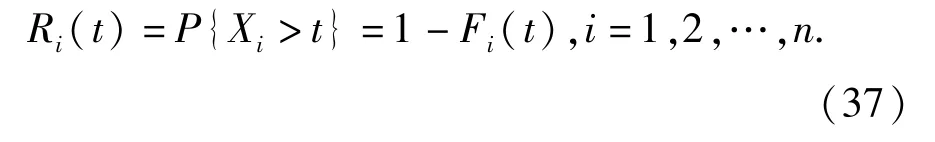
在串联系统中,一个子系统失效即导致整个系统的失效,因此,串联系统的可靠度可写为

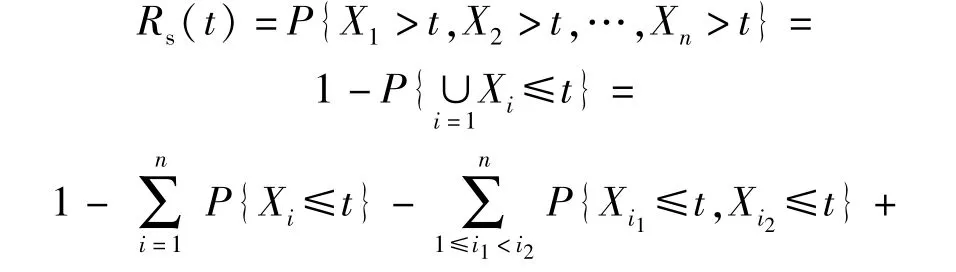
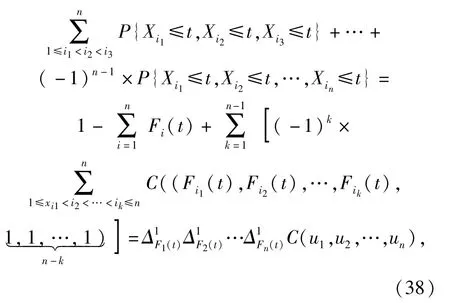
可知(35)式为利用失效率表示的系统可靠度,与不考虑故障相关性的串联系统可靠性Rs(t)=相比,可知考虑故障相关性的系统可靠性是将失效率的联合分布用Coupla函数代替:

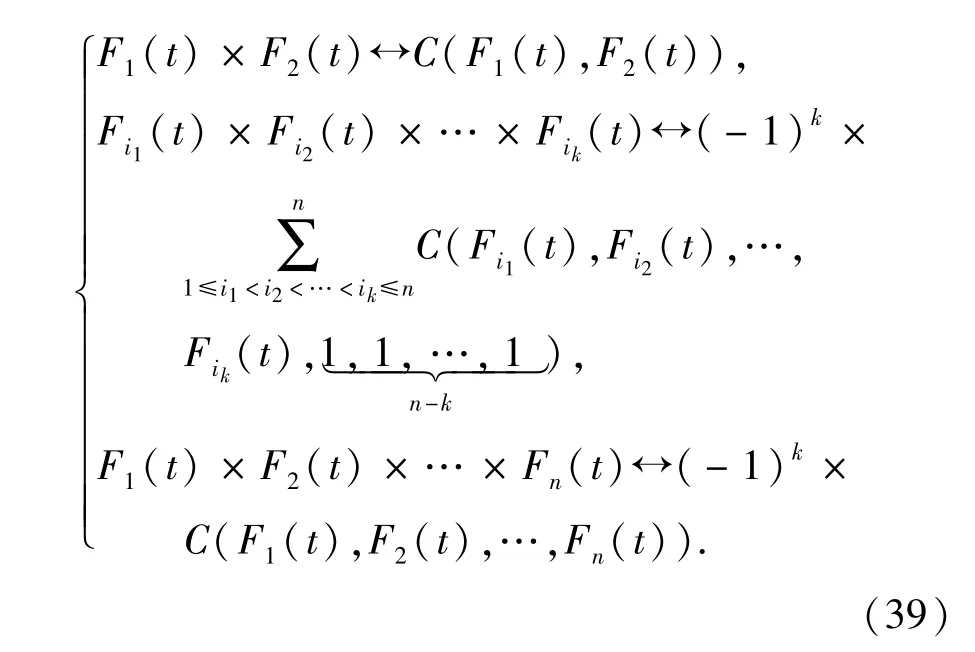
根据(36)式,可知对于任意n维Copula函数C(F1(t),F2(t),…,Fn(t)),均有与之唯一对应的n维Copula函数C(R1(t),R2(t),…,Rn(t))。因此,对于具有故障相关性的子系统,将(37)式代入(38)式,可得到用子系统可靠度表示的串联系统可靠度[18]:

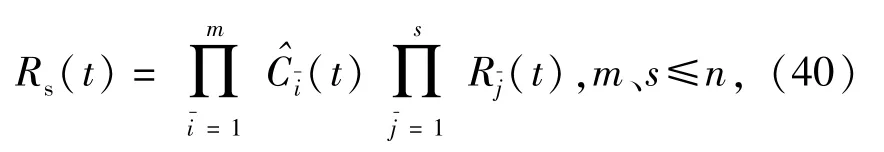
由(39)式可知,若串联系统中无故障相关子系统,则系统的可靠度为

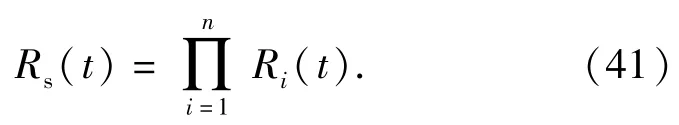
(41)式即为传统的串联系统可靠度计算式。

为说明故障相关性对串联系统可靠性的影响,设系统中每个子系统的初始可靠度均为0.9,图2所示为串联系统故障相关可靠性(相关系数倒数θ-1=0.2)及故障独立可靠性随子系统数目的变化情况。

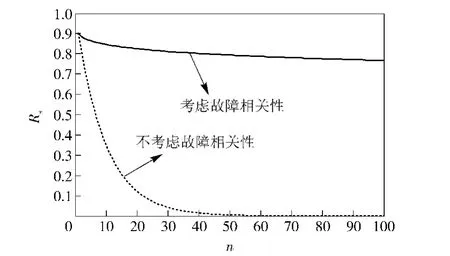
图2 故障相关及独立的串联系统可靠性变化Fig.2 System reliability by considering failure correlation and independence

若假设串联系统由4个子系统组成,其初始可靠度为

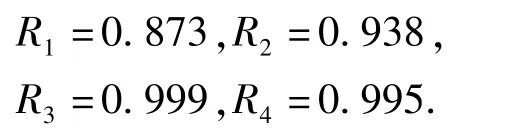
则其故障相关可靠度随故障相关系数θ的变化如图3所示。

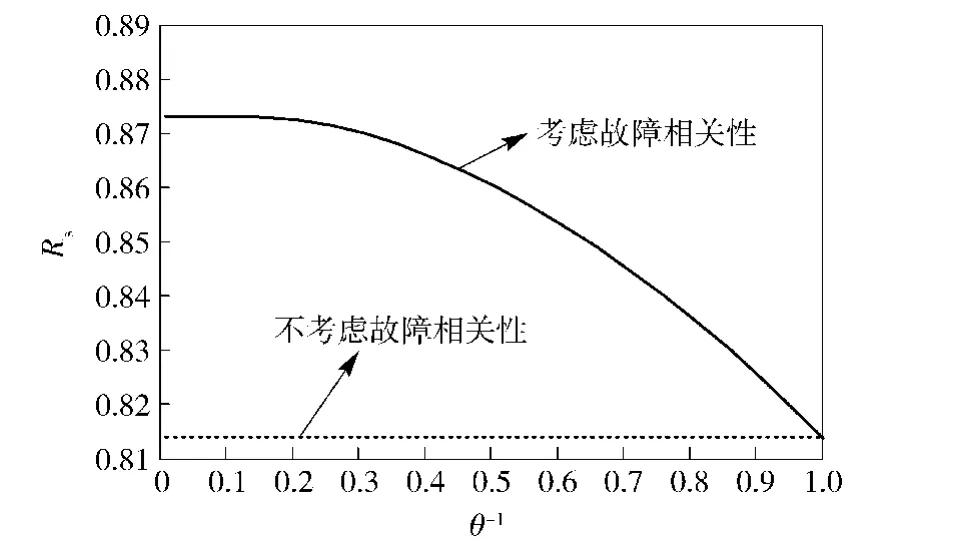
图3 串联系统故障相关可靠度随相关系数的变化Fig.3 System reliability vs.correlation coefficient

由图2和图3可知,考虑故障相关性后,串联系统可靠性有很大提高。另外,由图3可知,当θ→+∞时,子系统完全相关,θ=1时,子系统完全独立。

由(7)式可知:

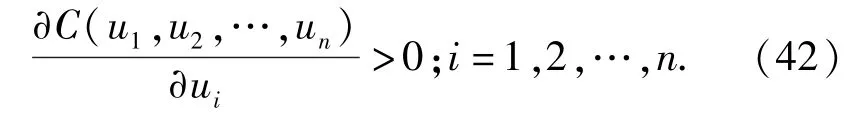
由(41)式可知,计算考虑故障相关性的可靠性时,如(39)式,系统可靠性为子系统的可靠性的增函数。这就意味着在同样的可靠性要求下,与传统的串联系统分配方法相比,考虑故障相关性可降低子系统分配的可靠性,从而降低加工制造成本。

3.3 考虑故障相关度的分配方法

显然,若某一个子系统与其他更多的子系统具有故障相关性,那么就认为这个子系统具有更高的相关失效严重度。根据(36)式,定义第i个子系统的相关失效严重度为:

一个子系统与其自身的故障一定是完全相关的,即τii=1为避免出现分母为0的情况,(43)式仍然保留τii项。因此,若两个子系统均独立,二者的失效率分配相对值均为

根据(43)式和(30)式得到相关失效严重度的是效率分配相对值,结合非线性转换函数,根据(14)式～(21)式的过程即可得到子系统失效率分配系数比值。在(21)式中,对λ1进行归一化处理,得

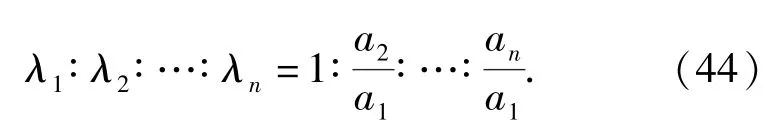
t时刻第i个子系统可靠度为

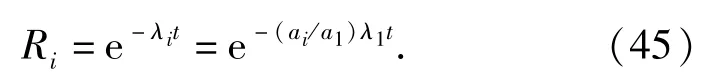
将(44)式代入(4)式,可得

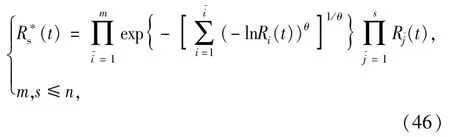
求解(46)式可得λ1的值,进而得到子系统失效率分配系数。

4 算例

针对本文提出的可靠性分配方法,通过分析CNC主轴系统进行说明与验证。本例中选取的6项分配指标,分别为:失效频率(k=1),失效严重度(k=2),复杂度(k=3),加工难度(k=4),工作环境(k=5)和成本(k=6).另外,对比相关失效严重度(k=7)对可靠性分配结果的影响。

不同失效模式下的失效频率和失效严重度如表1所示,其中,子系统的失效频率和失效严重度可由下式[7]得出:

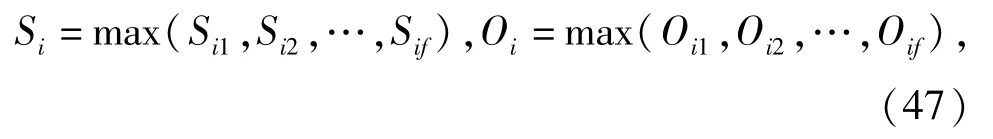
式中:Sif、Oif分别为第f个失效模式下的失效严重度和失效频率。

子系统k=3至k=6指标如表2所示。

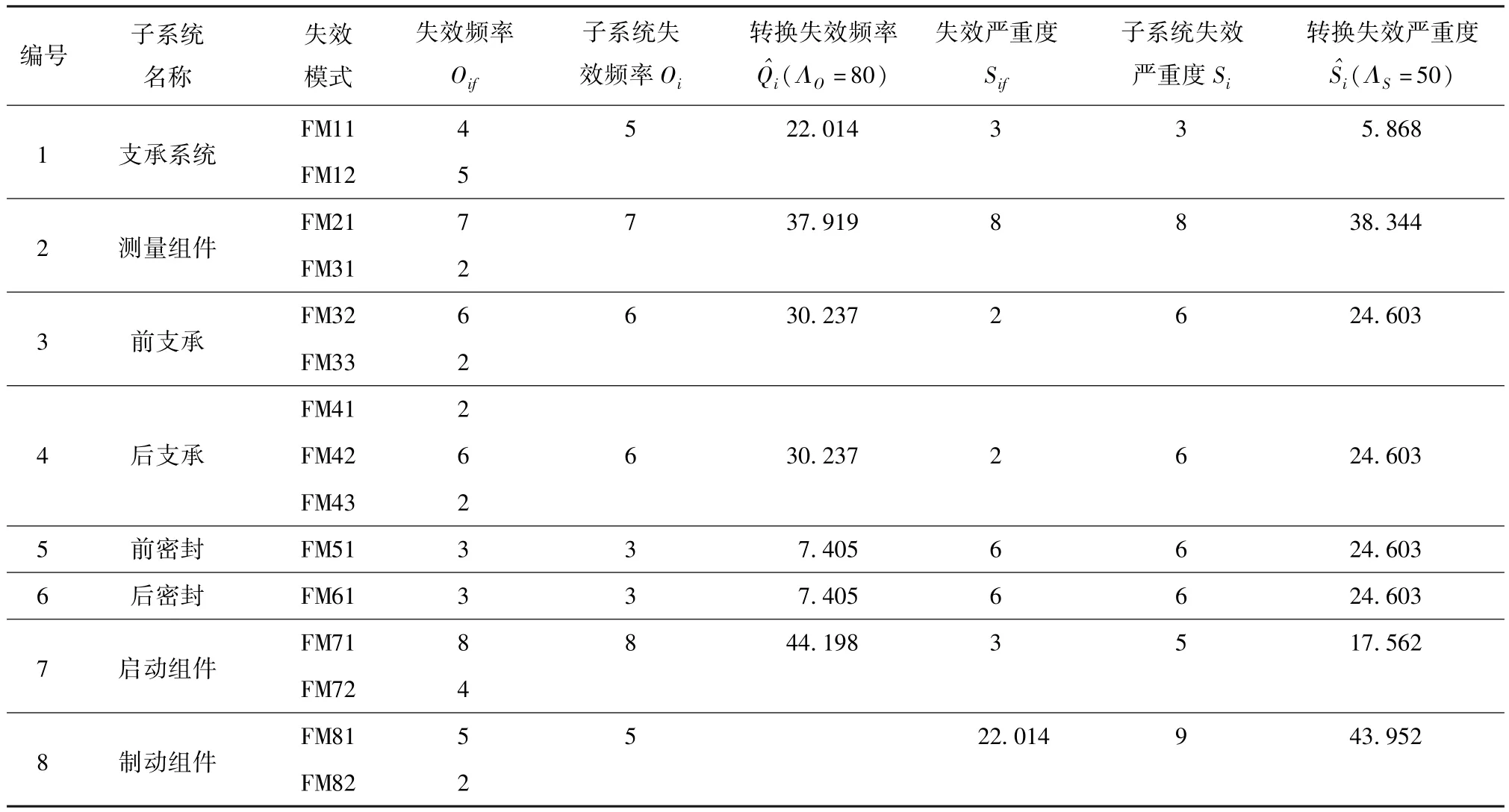
表1 CNC主轴系统FMEA分析Tab.1 FMEA of lathe’s spindle system

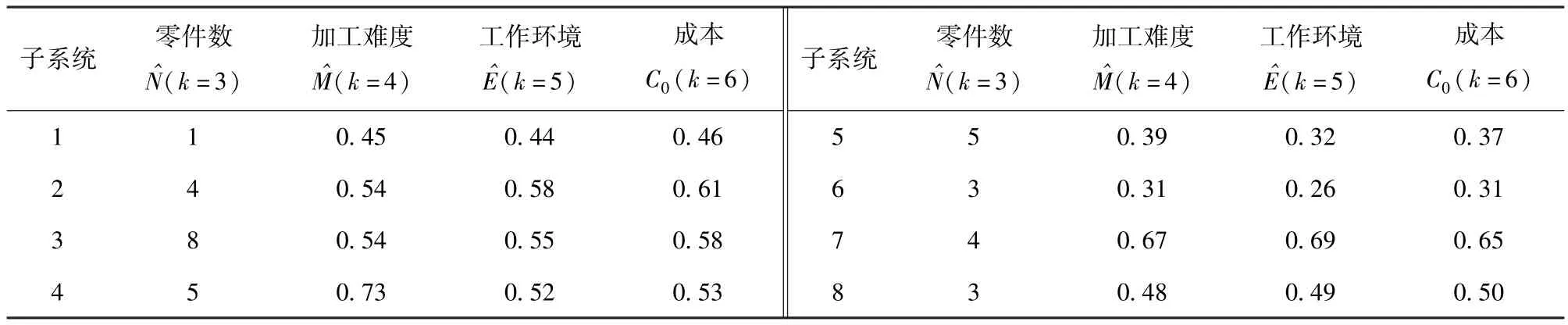
表2 子系统k=3至k=6指标值Tab.2 Criterions of k=3 to k=6 of subsystem

考虑各子系统间的故障相关性,可通过故障信息的统计数据,由2.2节所述的估计方法计算相关系数θ,并由(34)式计算相关性矩阵元素的值。

根据沈阳机床厂在2010年1月至2011年3月间,对HTC2050型号机床的监测故障信息进行统计,可得到相关性矩阵为

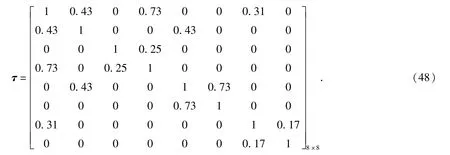
由(48)式可得,各子系统的相关严重度向量为

不考虑故障相关性时,根据(13)式～(16)式,可得分配矩阵Γindep为

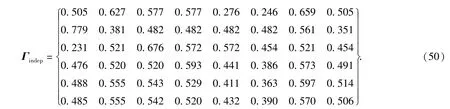
权重向量Windep为

因此,分配向量Aindep为

由(45)式可知,失效概率分配系数的比值为

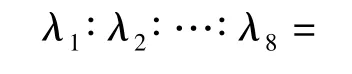
若要求t=500 h时,系统的可靠度为0.99,不考虑故障相关性时,子系统的可靠度为

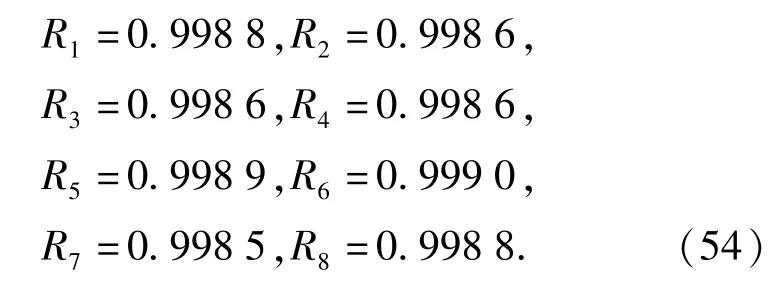
考虑故障相关性时,根据(48)式,得到计入相关严重度的分配矩阵Γdep:

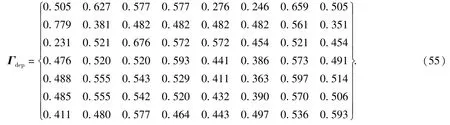
权重向量Wdep为

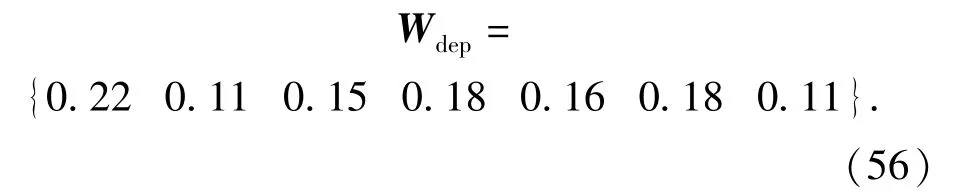
失效概率分配系数的比值为

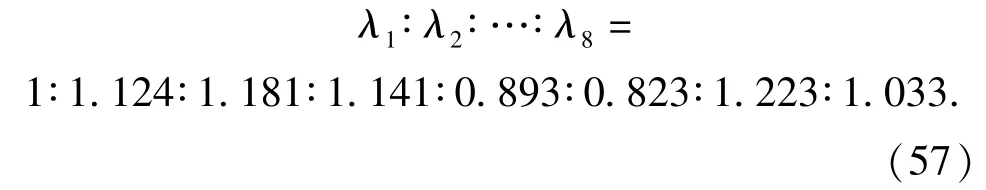
根据主轴故障频率分析,可知8个子系统的故障模式均直接或间接相关,近似取 θ-1=0.3,由(39)式可知:

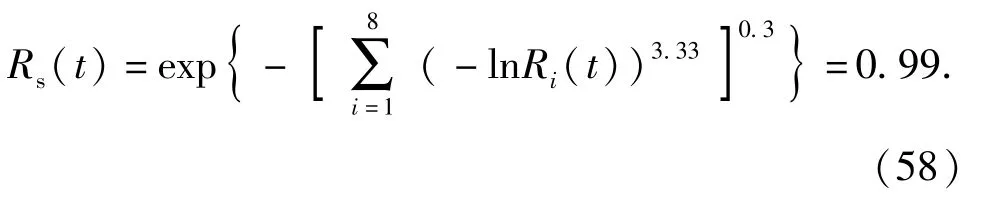
t=500 h时,子系统的可靠度为

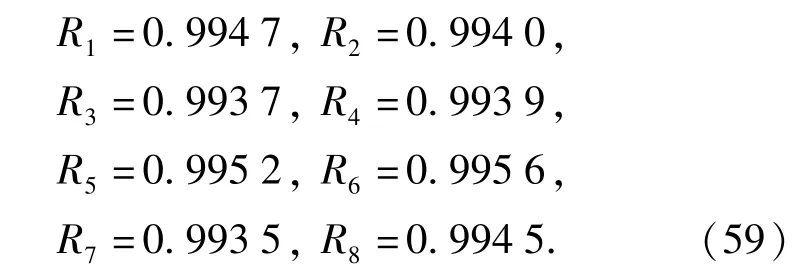
对比(54)式和(59)式可知,考虑故障相关性,可在串联系统要求相同时,给各子系统分配较低的可靠度。

5 结论

本文结合FMEA非线性修正函数,考虑故障相关性影响,基于Copula函数建立一种串联系统的可靠性分配方法。通过对某CNC主轴系统的可靠性分配实例,分析了该方法的有效性和特点。具体结论如下:

1)建立FMEA分析中严重度及失效频率的非线性转换关系,定义为严重度及失效频率的3阶多项式。FMEA 3阶非线性转换函数能够分别针对高、中、低3个区间进行分析,扩展了指数转换函数的应用范围。

2)考虑故障相关性,推导了基于Copula函数的串联系统可靠度计算公式。定义了相关性系数矩阵,并依据该系数矩阵确定了子系统相关严重度。将相关严重度作为一个分配指标,使得分配结果更加合理。

3)以某型CNC主轴系统为例,考虑故障相关性对主轴系统的子系统进行可靠性分配。通过与不考虑故障相关性的分配结果比较,可知考虑故障相关性时,与不考虑相关性的情况相比,子系统能够分配较低的可靠度,从而降低制造及维修成本。

需要注意的是,本文所述方法适用于可视为串联结构的系统,如数控机床及非储备系统等的可靠性分配问题。同时,本文对故障相关性的讨论中,并未考虑故障相关性随时间的变化,因此该方法并不适用于系统可靠性的动态分析。此外,运用本文所述方法进行可靠性分配,需要注意以下问题:

1)需要通过经验人为地确定可靠性区分度ΛS.在实际应用中,可依次选取不同的可靠性区分度进行验算,以便获得合理的ΛS值。

2)利用Copula函数对故障相关性进行描述具有一定的普遍意义,但并不是对所有故障相关问题都适用。在使用本文方法前,需要根据先验知识判断子系统故障相关性的描述方法,选择合理的函数进行运算。

References)

[1]Hudoklin A,Rozman V.Reliability allocation[J].Elektrotehniski Vestnik,1980,47(1):10-14.

[2]Keller A Z,Kamath A R R,Perera U D.Reliability analysis of CNC machine tools[J].Reliability Engineering,1982,3(6): 449-473.

[3]Wu J,Deng C,Shao X Y,et al.A reliability assessment method based on support vector machines for CNC equipment[J].Science in China Series E:Technological Sciences,2009,52(7): 1849-1857.

[4]樊少华.基于模糊理论的数控车床可靠性分配[D].长春:吉林大学,2011.FAN Shao-hua.Reliability allocation of CNC lathe based on fuzzytheory[D].Changchun:Jilin University,2011.(in Chinese)

[5]Wang Y,Jia Y,Yu J,et al.Field failure database of CNC lathes [J].International Journal of Quality&Reliability Management,1999,16(4):330-343.

[6]Wang Y,Jia Y,Yu J,et al.Failure probabilistic model of CNC lathes[J].Reliability Engineering&System Safety,1999,65(3):307-314.

[7]Wang Y,Yam R,Zuo M J,et al.A comprehensive reliability allocation method for design of CNC lathes[J].Reliability Engineering&System Safety,2001,72(3):247-252.

[8]Itabashi C R R,Yadav O P.System reliability allocation based on FMEA criticality[J].Automotive Electronics Reliability,2009,2.

[9]Kim K O,Yang Y,Zuo M J.A new reliability allocation weight for reducing the occurrence of severe failure effects[J].Reliability Engineering&System Safety,2013,117(2):81-88.

[10]Yadav O P,Zhuang X.A practical reliability allocation method considering modified criticality factors[J].Reliability Engineering&System Safety,2014,129:57-65.

[11]Mou P,Tao F,Jia C,et al.A copula-based function model in fuzzy reliability analysis on the planetary steering gear[C]//International Conference on Quality,Reliability,Risk,Maintenance,and Safety Engineering.Emeishan,China:IEEE,2013: 375-378.

[12]Huang M,Wang Q,Li Y,et al.An approach for improvement of avionics reliability assessment based on copula theory[C]//9th International Conference on Reliability,Maintainability and Safety.Guiyang,China:IEEE,2011:179-183.

[13]Chen Z Z,Liu Y,Huang H Z,et al.A reliability Allocation method considering failure dependence[C]//ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.Portland,Orgen: American Society of Mechanical Engineers,2013.

[14]李霞.COPULA方法及其应用[M].北京:经济管理出版社,2014.LI Xia.COPULA method and its application[M].Beijing:Economic Management Press,2014.(in Chinese)

[15]易文德.应用Copula探讨可靠性理论中的相依性[D].成都:西南交通大学,2005.YI Wen-de.Applying Copula to study the dependence of reliability[D].Chengdu:Southwest Jiaotong University,2005.(in Chinese)

[16]Sklar A.Random variables,distribution functions,and copulas: a personal look backward and forward[J].Lecture Notes-Monograph Series,1996,28:1-14.

[17]Yang Z,Zhu Y P,Ren H R,et al.Comprehensive reliability allocation method for CNC lathes based on cubic transformed functions of failure mode and effects analysis[J].Chinese Journal of Mechanical Engineering,2015,28(2):315-324.

[18]张英芝,郑锐,申桂香,等.基于Copula理论的数控装备故障相关性[J].吉林大学学报:工学版,2011(6):636-640.ZHANG Ying-zhi,ZHENG Rui,SHEN Gui-xiang,et al.Failure dependency of CNC equipment based on Copula theory[J].Journal of Jilin University:Engineering and Technology Edition,2011(6):636-640.(in Chinese)

A Comprehensive Reliability Allocation Method for Numerical-controlled Lathes Based on Copula Function

YANG Zhou,ZHU Yun-peng,ZHANG Yi-min,REN Hong-rui
(School of Mechanical Engineering and Automation,Northeastern University,Shenyang 110819,Liaoning,China)

An allocation method which considers fault correlation is proposed for the reliability allocation of series systems based on the non-linear transform functions of failure mode and effects analysis (FMEA).In consideration of the multiple factors that affect the reliability allocation,an reliability allocation matrix is established by employing the significance factors.The non-linear transform laws of failure severity and failure frequency are established to address the limitation of FMEA.A coefficient matrix of fault correlation is established based on Gumbel Copula function and Kendall correlation coefficients,and the correlated failure severities of subsystems are calculated.The equation of calculating the reliability of series system is derived based on Copula function.This equation is employed to guide the reliability allocation.Finally,the characteristics of the method are analyzed by taking a spindle system of a computerized numerical controlled(CNC)lathe for example.The allocation results are compared,which consideres dependent and independentfaults of subsystems.The result shows that the the allocation method withfault correlation can be used to provide the lower reliability allocation of subsystems,thus reducing the processing and maintenance costs.

machine tool technology;series system;reliability;failure mode and effects analysis;comprehensive reliability allocation;failure correlation

TB114.3

A

1000-1093(2016)01-0131-10

2015-05-22

国家自然科学基金项目(51135003、51205050、U1234208);“高档数控机床与基础制造装备"重大专项项目(2013ZX04011011);教育部新教师基金项目(20110042120020);中央高校基本科研业务费专项(N130503002);机械系统与振动国家重点实验室开放课题(MSV201402);辽宁省高等学校优秀人才支持计划项目(LJQ2014030)

杨周(1979—),女,副教授。E-mail:yangzhou@mail.neu.edu.cn.