静压止推气浮轴承动特性的微扰动法研究

卢志伟,马方杰,刘波,张君安

(西安工业大学机电工程学院,陕西西安710032)

静压止推气浮轴承动特性的微扰动法研究

卢志伟,马方杰,刘波,张君安

(西安工业大学机电工程学院,陕西西安710032)

为了实现对静压气浮轴承的动特性进行研究,提出并设计了一种具有可变截面积均压槽的静压气浮轴承,结合气浮轴承的力学振动模型采用微扰动法建立了气浮轴承动态控制方程,运用有限差分法对气浮轴承动态控制方程进行了数值求解,得到了气浮轴承的动态刚度和阻尼。计算结果表明:当振动较小时静压止推气浮轴承的动态刚度值与静态刚度值相当,在气膜间隙为5.5 μm左右时,气浮轴承的动、静刚度均达到最佳值;在同一供气压力下,随着气浮轴承气膜间隙的增大,其动阻尼呈非线性减小,气膜间隙对气浮轴承动阻尼系数的影响较大。

机械学;气浮轴承;微扰动;动刚度;动阻尼;有限差分

DOI:10.3969/j.issn.1000-1093.2016.01.022

0 引言

随着精密、超精密技术的发展,对气体静压轴承的刚度、精度及稳定性都提出了更高和更迫切的要求[1-2]。由于气体的可压缩性,对提高气体静压润滑轴承的气膜刚度带来很大的困难,因此提高气体静压轴承的刚度是气体静压轴承研究领域的难点和热点之一,属于前沿问题[3-4]。传统的气体静压止推轴承都采用小孔、环面、狭缝等节流阻抗固定的节流器,其承载能力和刚度的提高非常有限。对气浮轴承刚度进行反馈控制是实现高刚度甚至无穷静刚度的一条有效途径,近十几年来国内外开展了不少这方面的研究,但是在气浮轴承应用方面的进展并不明显[5]。为使气浮轴承刚度的提高有新突破,根据气膜间隙变化或相应的压力分布变化改变均压槽的截面积,在承载面采用弹性薄板来实现可变截面均压槽的气浮轴承是一种很有应用前景的新型高刚度气浮轴承[6]。精密与超精密加工技术伴随着科学的飞速发展应运而生,对作为精密与超精密加工设备重要部件的空气静压轴承的动静态性能提出了更为苛刻的要求[7-8]。气体本身固有性质的限制,给改善空气静压轴承的性能带来了诸多不便。因此,如何分析研究空气静压轴承的性能,并在此基础上优化空气静压轴承的结构,已然成为气体润滑技术领域的研究重点[9-10]。本文采用微扰动法对静压止推气浮轴承的动态性能进行了数值计算和仿真,并对气浮轴承动态刚度和阻尼的相关影响进行了分析和研究。

1 静压止推气浮轴承的结构设计

本文提出和设计了一种具有可变均压槽结构的高刚度气浮轴承,在气浮轴承的承载面上设计了一种环形弹性薄板结构,通过气膜压力反馈使环形弹性薄板产生弹性变形从而形成均压槽,引起均压槽深度的变化,从而达到提高气浮轴承刚度的目的。这种结构在气浮轴承的四角设置4个固有节流孔(喷嘴节流),用环形均压槽将节流器出口与弹性均压槽连通。本文所研究的弹性薄板气浮轴承的结构示意图如图1所示,图1中均压槽的位置和与弹性薄板直接接触的气腔位置是一致的,弹性薄板与气浮轴承本体是在其接触部位除气腔外的所有部分都用一种粘接强度比较好的粘接剂粘接在一起的。

弹性薄板气浮轴承的工作原理:气体由进气孔输入气浮轴承中,通过矩形带过渡圆角的槽型气腔,最后由节流孔输出到导轨工作表面形成压力气膜。当载荷增大或者减小时,弹性薄板沿槽型气腔方向内凹或者外凸,改变了节流孔的环面节流面积,并形成了可变深度的可变截面积均压槽,从而提高气浮轴承的刚度。制造过程中气浮轴承内的气腔中充满压力为p的气体,使承载面上弹性薄板外凸。加工完成后的自然状态下,气浮轴承的承载面上的弹性变形部分就出现了凹下去的初始均压槽。槽宽与气浮轴承内的气腔宽度一致,槽深与p的大小及均压槽的位置有关。设计上希望气浮轴承的载荷F和气膜厚度h的特性F(h)的曲线越接近垂线越好,即希望dF(h)/dh→∞.

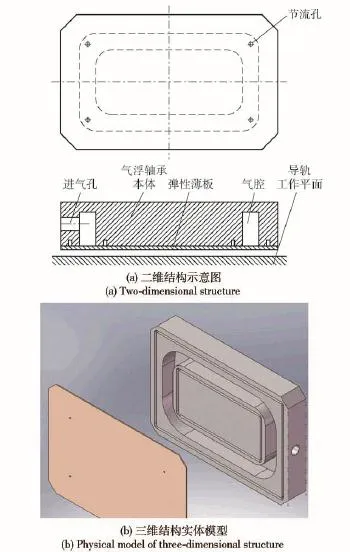
图1 止推气浮轴承的结构示意图Fig.1 Schematic diagram of aerostatic thrust bearings

2 控制方程及其数值分析

2.1 气浮轴承的物理及力学模型

气浮轴承的物理模型如图2(a)所示,供气压力为ps,由进气孔流入,经节流孔节流后压力降为p0,最后经气膜间隙流入大气,压力变为pa,气膜间隙内的压力为p(χ,y),外部载荷为F.为了便于研究,可以把图2(a)的模型简化为图2(b).气浮轴承的气膜具有一定的刚度K,加之气体具有一定粘性,气浮轴承在承载方向上具有阻尼C,其中K与C都是气膜间隙h的函数。因此,气浮轴承的物理模型也可看作是质量块m、弹簧K、阻尼器C构成的振动系统,如图2(c)所示。

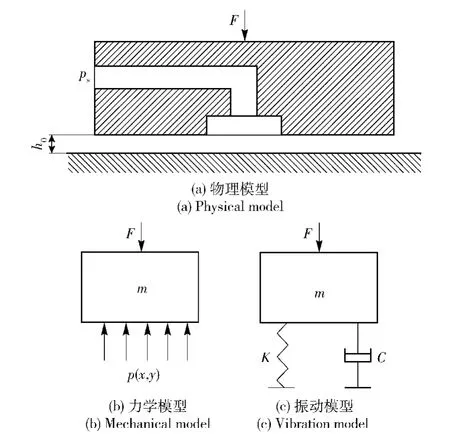
图2 气浮轴承的模型Fig.2 Models of gas bearings

对于图2(b),根据牛顿第二定律有

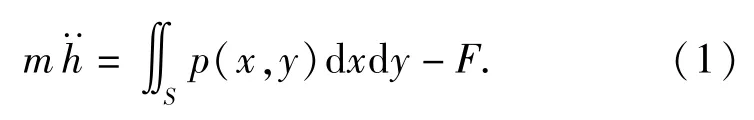
设定气浮轴承处在静平衡时的位置记为h0,给气浮轴承一个初始的小位移扰动Δh(Δh≪h0),那么任意时刻的气浮轴承的位置、压力、载荷分别可以表示为h=h0+Δh,p=p0+Δp,F=F0+ΔF,其中: Δp、ΔF分别为小扰动Δh所引起的气膜内压力和承载力的变化;h0、p0、F0为静态值;Δh、Δp、ΔF为增量。这种将一个参数量写为一个稳定量和一个扰动量之和,且扰动量远小于稳定量的方法成为微扰动法。

将h、p及F的表达式分别带入到代入(1)式中,并将承载力F在F0处作1阶泰勒公式展开通过联立求解得

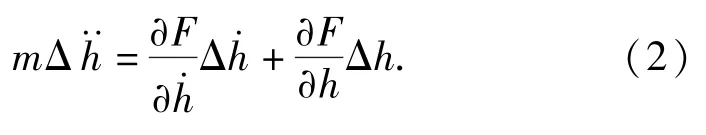
图1(c)所示的系统,由牛顿第二定律可知:

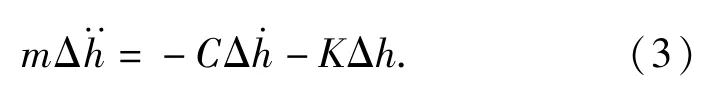
设cr=-C/2m,ωn=K/m,ωn是气浮轴承振动的自然频率,则(3)式变为

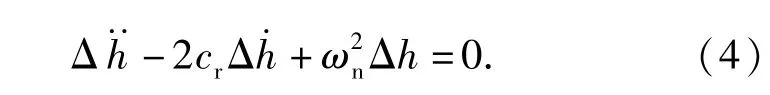
(4)式的特征方程的根为

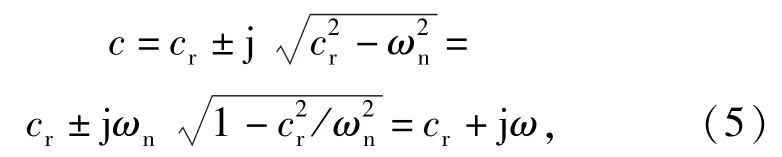
式中:ω是有阻尼时的振动频率,ω=±ωn·

2.2 微扰动法求解控制方程

静压止推气浮轴承的气体润滑状态分析主要以求解Reynolds方程为基础,气浮轴承的性能计算是在对Reynolds方程进行求解的基础上展开的。假定气浮轴承为刚体且气体与气浮轴承上表面并无相对滑动,经整理得到雷诺方程的表达式为

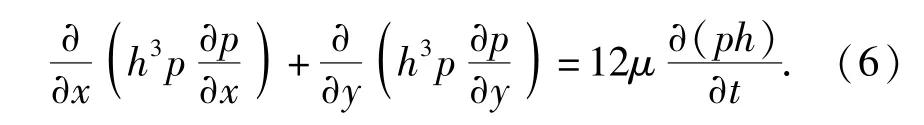
根据(6)式雷诺方程运用微扰法推导分解雷诺方程。将h=h0+Δh,p=p0+Δp分别代入式(6)得

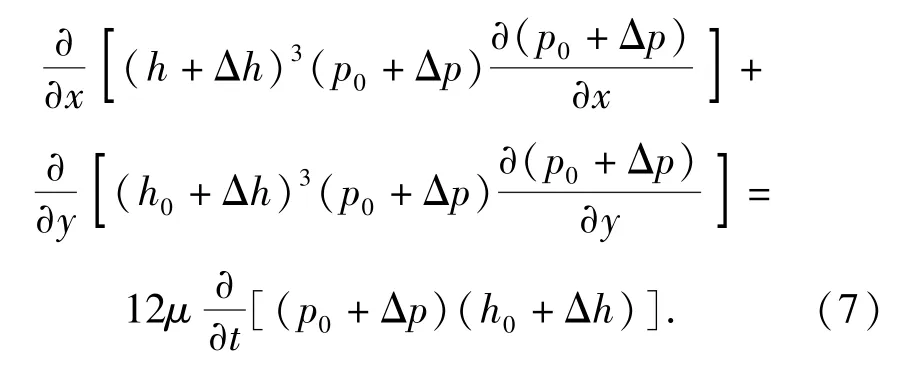
将(7)式等号两侧分别展开并忽略高阶无穷小量,并将推导得到的公式中与时间无关的稳定部分和与时间有关的扰动部分分开得到雷诺方程的稳态方程(8)式和瞬态方程式(9):

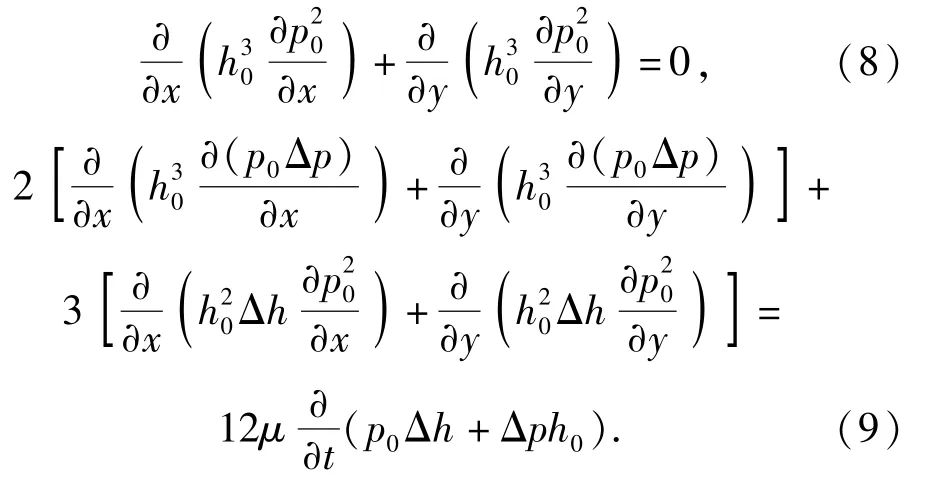
2.3 建立气浮轴承动态控制方程

在(9)式中,本文认为Δh、Δp的变化频率是近似相等的。由于当Δh减小时,Δp会随之增大,为计算方便可以假设二者相位之差为π,则可以将Δh、Δp写为Δh=εh0ect,Δp=(pR+jpI)ect,分别代入到(9)式中得到(10)式:

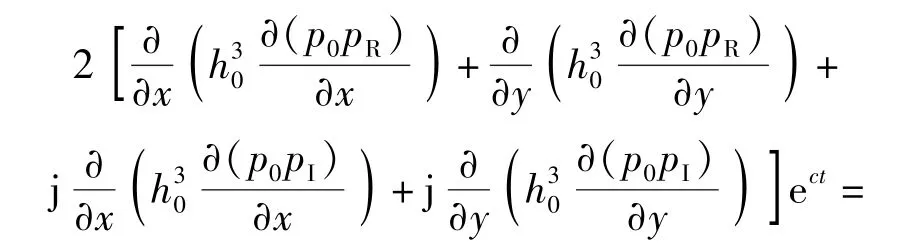
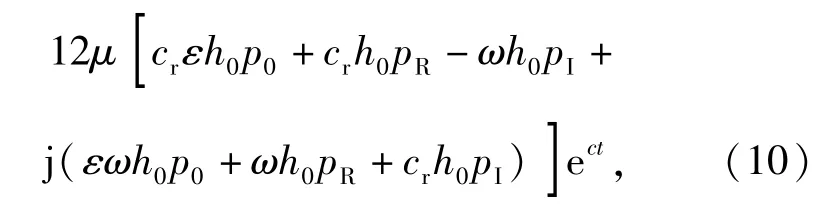
式中:ε为极小量扰动幅值率;pR为压力值实部;pI为压力值虚部。令(10)式两端实部与实部相等,虚部与虚部相等,得到(11)式和(12)式即为本文所研究的弹性气浮轴承的动态控制方程:

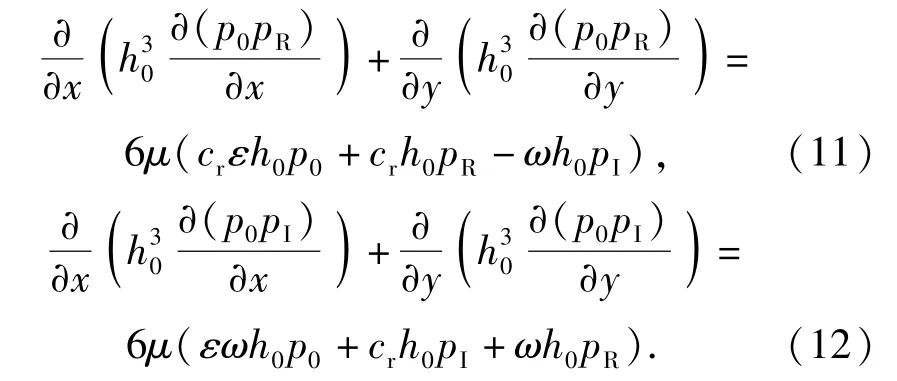
2.4 动态控制方程的数值差分

根据气浮轴承工作精度需求,本文的数值计算采用有限差分中2阶精度的差分格式,来离散化求解气浮轴承的动态控制方程。将(11)式与(12)式中的微分项用有限差分对公式进行离散化求解,得到(13)式和(14)式:

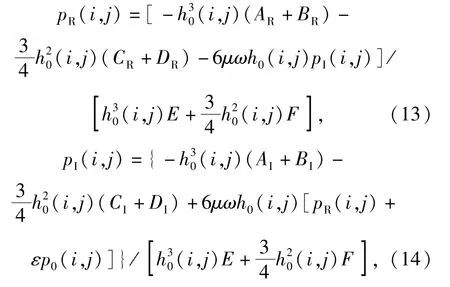
式中:AR、BR、CR、DR、AI、BI、CI、DI、E、F为与p0(i,j)、h0(i,j)、pI(i,j)、pR(i,j)等有关的系数。(14)式与(15)式中分别记pR(i,j)=R(i,j)、pI(i,j)=I(i,j),则采用超松弛迭代法求解(13)式与(14)式,其迭代公式分别为(15)式与(16)式:

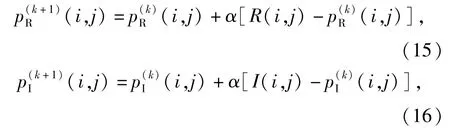
式中:k为迭代次数;α为迭代的加速收敛系数,一般情况下可以取1＜α＜2.

2.5 气浮轴承的动态刚度与阻尼的计算

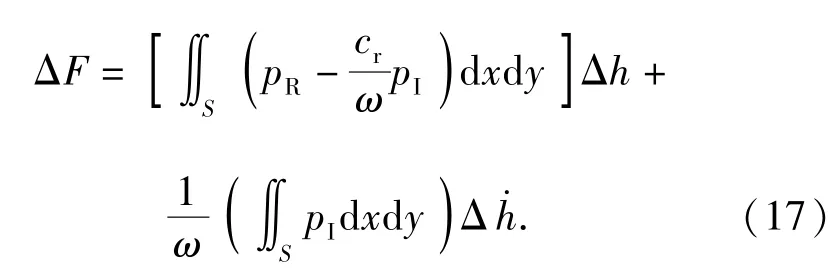
将承载力F在F0处作1阶泰勒公式展开并化简得到与(17)式进行比较以及结合可以得到气浮轴承支承的刚度与阻尼如(18)式:

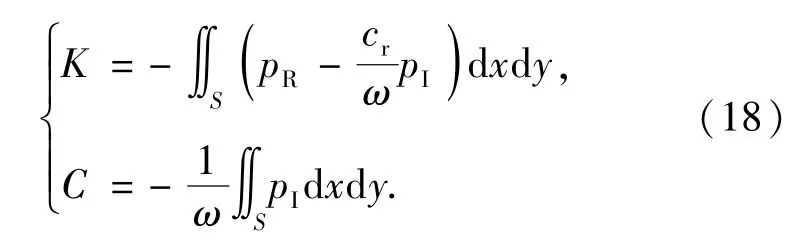
3 数值计算与分析

3.1 动态控制方程的求解差分流程

本文所研究的可变均压槽止推气浮轴承,其结构如图1所示。止推气浮轴承本体的长度为80 mm,宽度为50 mm,厚度为15 mm;弹性薄板的厚度为0.3 mm,弹性薄板材料为2Cr13,弹性模量E= 1.12 GPa;加工弹性薄板气浮轴承时供气压力为0.55 MPa,工作时的供气压力为0.65 MPa;取供气温度T0=300 K,绝热指数k=1.4,空气粘度μ= 1.833×10-5Pa·s,迭代收敛误差值σ=1×10-6.采用有限差分法对静压止推为研究对象进行研究,气膜压力分布按直角坐标和极坐标划分网格,两种网格重叠区域采用双线性插值传递计算信息,将气浮轴承在静态时的不同气膜间隙下的气膜压力分布值作为初始值代入气浮轴承动态控制方程(15)式与(16)式中进行求解,整个动态控制方程的求解差分流程图如图3所示。

3.2 计算结果及分析

根据所研究的气浮轴承的的结构和参数,按照动态控制方程的的求解差分流程图,运用VB语言采用有限差分方法对弹性薄板气浮轴承的动特性进行了数值计算,得出了不同气膜间隙下气浮轴承的动态刚度和阻尼系数。图4、图5为静压止推气浮轴承在不同气膜间隙下的动态刚度和动态阻尼数值计算结果。

图4为静压止推气浮轴承的动态刚度与静态刚度进行的对比曲线图。从图4可以看出:在气膜间隙h＜5.5 μm时,气浮轴承的动、静刚度随着气膜间隙的增大逐渐增大;当气膜间隙h＞5.5 μm时,气浮轴承的动、静刚度随着气膜间隙的增大逐渐变小;在气膜间隙h约为5.5 μm时,气浮轴承的动、静刚度均达到最佳刚度值。其次,从图4中也可以看出:气浮轴承的动态刚度值与静态刚度值十分接近,当振动很小时,动态刚度和静态刚度是基本相当的,使得静压气浮轴承在精密、超精密设备中运用来提高其刚度可以得到很好的发展。

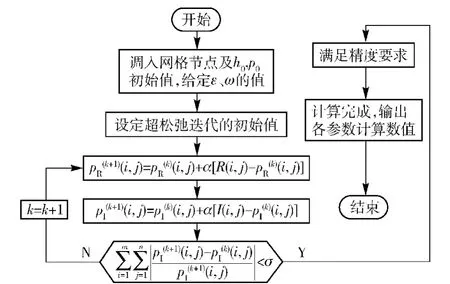
图3 控制方程求解流程图Fig.3 Flow chart of solving the control equations

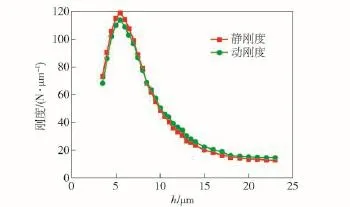
图4 气浮轴承动、静刚度的对比曲线Fig.4 Contrast curves of the static and dynamic stiffnesses of gas bearings

图5为静压止推气浮轴承在不同气膜间隙下的动阻尼系数变化情况。从图5中的计算结果与实验结果分析可以看出:气浮轴承的两曲线的动阻尼系数均随着气膜间隙h的增大而呈非线性减小,特别是气膜间隙h在3～10 μm的范围内气浮轴承阻尼系数减小的更加明显,气浮轴承的动阻尼受气膜间隙的影响比较大;从两条曲线可以看出其变化趋势趋于一致,这也很好地验证了理论计算的一致性。但在图5中气浮轴承的计算结果与实验结果也存在着一定的差异,引起这种现象的原因:尽管数学模型已考虑了很多主要影响因素,但还有一些因素影响较小而被忽略而引起了数值计算结果与实验结果有差异;数值计算中轴承表面假设为绝对光滑以及各设计参数须严格保证,但轴承在实际加工中存在着一定的表面质量误差,这也使得理论计算与实验结果存在一定的差异。

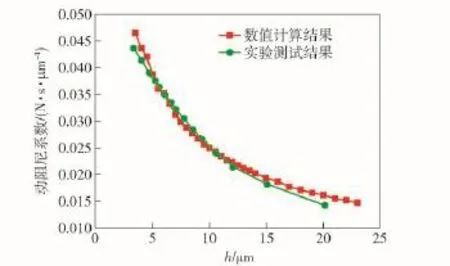
图5 气浮轴承动阻尼系数的数值计算与实验测试结果曲线Fig.5 Curves of numerical calculation and experimental results of dynamic damping coefficients of gas bearings

4 结论

1)本文提出并设计了一种具有可变截面积均压槽的气浮轴承,采用微扰动法通过数值分析计算得知当振动较小时其动态刚度值与静态刚度值相当,在气膜间隙h为5.5 μm左右时气浮轴承的动、静刚度均达到最佳值。

2)在同一供气压力p下,随着气浮轴承的气膜厚度h的增大,其动阻尼C呈非线性的减小,且存在一个最佳间隙h,此时气浮轴承的静动刚度K可以达到一个最佳值。

3)在设计的新型气浮轴承本体中气腔的结构和位置对弹性薄板的变形以及气浮轴承的承载力F和其刚度K及阻尼C影响都非常大,因此如何进一步更好地提高气浮轴承的静、动刚度以及动阻尼乃至其整体性能需要进行优化创新设计,需要进一步探索和研究。

References)

[1]叶燚玺.超精密运动平台中气浮支承振动特性的研究[D].武汉:华中科技大学,2010.YE Yi-xi.Vibration characteristics of aerostatic bearing in ultraprecision motion stage[D].Wuhan:Huazhong University of Science and Technology,2010.(in Chinese)

[2]Belforte G,Raparelli T,Viktorov V,et al.Discharge coefficients of orifice-type restrictor for aerostatic bearings[J].Tribology International,2007,40(3):512-521.

[3]吕延军,虞烈,刘恒.流体动压滑动轴承-转子系统非线性动力特性及稳定性[J].摩擦学学报,2005,25(1):61-66.LYU Yan-jun,YU Lie,LIU Heng.Stability and nonlinear dynamic behavior of a hydrodynamic journal bearing-rotor system[J].Tribology,2005,25(1):61-66.(in Chinese)

[4]张广辉,刘占生,田新.旋转冲压转子-动静混合气体轴承系统振动特性仿真研究[J].振动与冲击,2010,29(9): 160-165.ZHANG Guang-hui,LIU Zhan-sheng,TIAN Xin.Numerical study on vibration characteristics of rotor-hybrid gas bearings system in rotating ram jet[J].Journal of Vibration and Shock,2010,29(9):160-165.(in Chinese)

[5]Chen M F,Lin Y T.Static behavior and dynamic stability analysis of grooved rectangular aerostatic thrust bearings by modified resistance network method[J].Tribology International,2002,35(5): 329-338.

[6]张君安,张文豪,廖波,等.具有可变均压槽的气体静压推力轴承的性能研究[J].摩擦学学报,2009,29(4):329-334.ZHANG Jun-an,ZHANG Wen-hao,LIAO Bo,et al.Study on characteristics of air static pressure thrust bearing with variablesection pressure equalizing groove[J].Tribology,2009,29(4): 329-334.(in Chinese)

[7]Chen X D,Chen H,Luo X,et al.Air vortices and nano-vibrationof aerostatic bearings[J].Tribology Letters,2011,42(2): 179-183.

[8]Chen X D,Zhu J C,Chen H.Dynamic characteristics of ultraprecision aerostatic bearings[J].Advances in Manufacturing,2013(1):82-86.

[9]周权,侯予,陈汝刚.应用于高速透平膨胀机的箔片动压气体止推轴承的试验研究[J].西安交通大学学报,2012,46(11): 49-52.ZHOU Quan,HOU Yu,CHEN Ru-gang.Experimental research on compliant foil thrust bearings for high speed turbine expander [J].Journal of Xi'an Jiaotong University,2012,46(11):49-52.(in Chinese)

[10]孙昂,马文琦,王祖温.平面静压气浮轴承的超声速流场特性[J].机械工程学报,2010,46(9):113-119.SUN Ang,MA Wen-qi,WANG Zu-wen.Characteristics of subsonic velocity field of externally pressurized gas thrust bearings [J].Journal of Mechanical Engineering.2010,46(9):329-334.(in Chinese)

Research on Dynamic Characteristics of Aerostatic Thrust Bearings Based on Perturbation Method

LU Zhi-wei,MA Fang-jie,LIU Bo,ZHANG Jun-an
(School of Mechatronic Engineering,Xi'an Technological University,Xi’an 710032,Shaanxi,China)

An aerostatic thrust bearing with pressure-equalizing groove with variable sectional area is designed to research the dynamic characteristics of aerostatic thrust bearing.Based on the mechanical vibration model of gas bearings,the dynamic control equations of gas bearings is established by using perturbation method,and the dynamic control equations are sovled to obtain the dynamic stiffness and damping of gas bearings by the finite difference method.The results show that the dynamic and static stiffness values of aerostatic thrust bearings are equal when the vibration is small,and the dynamic and static stiffnesses of gas bearings reach the optimum value when the gas film thickness is about 5.5 μm;the dynamic damping decreases nonlinearly with the increase in gas film thickness at the same air supply pressure,and the gas film thickness greatly affects the dynamic damping coefficients of air bearings.

mechanics;gas bearing;perturbation;dynamic stiffness;dynamic damping;finite difference

TH133.36

A

1000-1093(2016)01-0149-06

2014-11-17

国家自然科学基金项目(50805112);陕西省教育厅重点实验室基金项目(15JS043)

卢志伟(1979—),男,讲师,硕士。E-mail:luzw8866@163.com