一类高阶常系数线性微分方程的特解公式

张守贵

(重庆师范大学数学科学学院， 重庆　401331)



一类高阶常系数线性微分方程的特解公式

张守贵

(重庆师范大学数学科学学院， 重庆401331)

高阶微分方程是常微分方程和高等数学的重要内容，但是现有的方法比较难掌握。对一类常见的高阶非齐次常系数线性常微分方程得到了求其特解的一般公式。首先引入了有关两个函数乘积高阶导数的莱布尼兹公式和一个组合数性质，然后利用待定系数法得到了求解该方程特解的一般公式。并给出了详细的证明过程和若干具体算例。结果表明：该方法的公式推导过程非常简单，所得公式有较高的实用性和有效性。

n阶线性常微分方程；特解公式；待定系数法；莱布尼兹公式

高阶常系数线性常微分方程解法是常微分方程和高等数学中一个重要组成部分。大部分文献只介绍了采用比较系数法、复数法、拉普拉斯变换法与常数变易法等求解这一类非齐次问题的特解[1-8]。但是这些方法的计算往往比较繁琐。对一类特殊的高阶常系数非齐次线性常微分方程，本文利用比较系数法给出了求特解的一般公式[9-17]。使得求解这一类问题的特解变得非常简单。

1　预备知识

如果函数u(t)、v(t)均m阶可导，则有：

(1)

这一公式通常叫做莱布尼兹(Leibniz)公式[18]。

(2)

式(2)为组合数的一个基本性质。

2　主要结果

推导非齐次n阶常系数线性常微分方程：

(3)

特解的一般公式方程(3)所对应齐次方程

其特征方程为：

rn+a1rn-1+…+an-1r+an=0

(4)

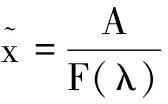
对λ是k重根的情形给予证明，不是特征根的情形同理可证。

证明用待定系数法求方程(3)的一个特解。由于λ是特征方程(4)的k重根，则可令其特解为：

(5)

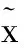
(m=1,2,…,k)

(6)

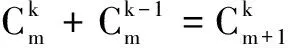
(m=k+1,k+2,…,n)

(7)

将式(6)和式(7)代入方程(3)得

B[n(n-1)…(n-k+1)λn-k+n(n-1)…

(n-k)λn-k-1t+…+nλn-1tk-1+λntk]eλt+

a1B[(n-1)…(n-k)λn-k-1+(n-1)…

(n-k+1)λn-kt+…+

(n-1)λn-2tk-1+λn-1tk]eλt+…+

an-1B[ktk-1+λtk]eλt+anBtkeλt=

B[n(n-1)…(n-k+1)λn-k+

a1(n-1)…(n-k)λn-k-1+…+an-kk!λk]eλt+

B[n(n-1)…(n-k)λn-k-1+

a1(n-1)…(n-k+1)λn-k-2+…+

an-kk(k-1)…2λk-1]teλt+

B[n(n-1)…(n-k)λn-k-1+a1(n-1)…

(n-k+1)λn-k-2+…+an-1λ+an]tkeλt=

BF(k)(λ)eλt+BF(k-1)(λ)teλt+…+

BF′(λ)tk-1eλt+BF(λ)tkeλt=Aeλt

由于λ是特征方程(4)的k重根，则有F(λ)=F′(λ)=…=F(k-1)(λ)=0，且F(k)(λ)≠0，从而有

BF(k)(λ)eλt=Aeλt

3　应用举例

解因为λ=-1不是特征方程F(r)=r2+2r+5=0的根，因此由定理1可以直接得到方程的特解：

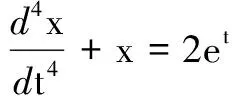
解因为λ=1不是特征方程F(r)=r4+1=0的根，由定理1可以直接得到方程的特解：

解因为λ=1是特征方程F(r)=r3-1=0的单根，因此由定理1可得方程的特解：

解因为λ=2是特征方程F(r)=r2-4r+4=0的二重根，因此由定理1可得方程的特解：

4　结束语

利用待定系数法和莱布尼兹公式，得出求解一类高阶常系数非齐次线性微分方程特解的一般公式，若干算例表明该方法计算十分简便，是求解这一类问题特解的实用方法。

[1] 王高雄.常微分方程[M].北京:高等教育出版社,2013.

[2] 张伟年,杜正东,徐冰.常微分方程[M].北京:高等教育出版社,2014.

[3] 张祥.常微分方程[M].北京:科学出版社,2015.

[4] 焦宝聪.常微分方程[M].北京:清华大学出版社,2008.

[5] 袁荣.常微分方程[M].北京:高等教育出版社,2012.

[6] 严国政.常微分方程[M].北京:科学出版社,2012.

[7] 同济大学数学系.高等数学[M].北京:高等教育出版社,2014.

[8] 刘浩荣,郭景德.高等数学[M].上海:同济大学出版社,2015.

[9] 张建梅,孙志田,崔宁.关于y″+py′+qy=Aeαt的特解[J].高等数学研究,2005,8(3):14-15.

[10] 池春姬.方程y″+py′+qy=eλt(Acosωx+Bsinωx)特解的一般公式[J].长春理工大学学报,2007,2(2):135-136,179.

[11] 张守贵.一类二阶常系数微分方程特解的教学探讨[J].重庆工商大学学报,2012,29(12):11-14.

[12] 刘文武,韦煜.n阶非齐次线性微分方程的一个特解公式[J].西南民族大学学报,2004,30(1):12-15.

[13] 赵士银.n阶常系数线性微分方程的特解公式[J].四川理工学院学报,2008,21(2):4-7.

[14] 李岚.二阶常系数非齐次线性微分方程特解的简便解法[J].四川理工学院学报,2013,26(4):93-96.

[15] 刘颖,方有康.有限递推法与待定系数法的计算复杂性比较——用于求y″+py′+qy=Pm(x)eaxcosbx或(sinbx)y的特解时[J].数学的实践与认识,2014,44(17):316-321.

[16] 王华,黄俊杰,阿拉坦仓.二阶常系数非齐次线性常微分方程通解的分离变量法[J].数学的实践与认识,2013,43(13):260-263.

[17] 杨继明,苏亚丽,李周红.常系数线非齐次性微分方程的特解公式[J].数学的实践与认识,2011,41(7):244-246.

[18] 刘正荣,杨启贵,刘深泉,等.数学分析[M].北京:科学出版社,2012.

TheFormulaofSpecialSolutionforaKindofHigh-orderLinearDifferentialEquationwithConstantCoefficients

ZHANG Shougui

(SchoolofMathematicsScience,ChongqingNormalUniversity,Chongqing401331,China)

High-orderdifferentialequationisanimportantcontentincoursesofordinarydifferentialequationandadvancedmathematics,butexistingmethodsaredifficulttobemastered.Forakindofn-orderlinearandnon-homogeneousordinarydifferentialequationwithconstantcoefficients,thegeneralformulaofthespecialsolutionsispresentedinthispaper.TheLeibnizformulaforhigherorderderivativesofproductoftwofunctionsandapropertyforthenumberofcombinationsarefirstintroduced,andthegeneralformulaofthespecialsolutionsfortheequationisobtainedbymethodofundeterminedcoefficients.Theprocessofproofsandsomeexamplesarealsogivenindetail．Theresultsshowtheformulaisverysimpleandillustratetheeffectivenessandpracticalityofthemethodpresented.

n-orderordinarydifferentialequation;formulaofspecialsolutions;methodofundeterminedcoefficients;Leibnizformula

2016-04-12

国家自然科学基金项目(11471063)

张守贵(1973-)，男，四川泸县人，副教授，博士，主要从事微分方程数值解方面的研究，(E-mail)shgzhang9621@sina.com

1673-1549(2016)03-0093-03

10.11863/j.suse.2016.03.19

O175.1

A