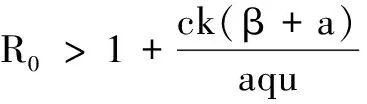具有免疫应答的HIV感染模型的稳定性
2016-11-04田海燕郭建敏郭彩霞
田海燕, 郭建敏, 郭彩霞
(大同大学数学与计算机科学学院, 山西 大同 037009)
具有免疫应答的HIV感染模型的稳定性
田海燕, 郭建敏, 郭彩霞
(大同大学数学与计算机科学学院, 山西大同037009)
建立具有HollingII感染率且考虑免疫应答的HIV模型,讨论系统解的非负性和有界性,得到确定模型动力学性态的基本再生数,最后通过分析模型在平衡点处相应的特征方程,利用微分方程基本理论,证明模型在正平衡点处是局部渐近稳定的。即人类免疫缺陷病毒HIV将在个体体内持续存在,并且免疫应答会持续起作用,并用数值模拟验证结果。
病毒感染;稳定性;免疫应答;正平衡点
引 言
目前,传染病仍然是人类身体健康的一大公敌,因为一些传染病传播速度快,直接影响到人类的生存和发展。人类免疫缺陷病毒HIV是一种感染人类免疫系统细胞的慢性病毒,属于反转录病毒的一种。1983年,人类免疫缺陷病毒在美国首次被发现。该病毒破坏人体的免疫能力,导致免疫系统失去抵抗力,从而导致人体感染各种疾病。HIV主要攻击人体的T淋巴细胞系统,一旦侵入机体细胞,病毒将会和细胞整合在一起终生难以消除[1-5]。因此,建立传染病的动力学模型,研究其发病原因,流行规律,尤其是找寻相应的防治措施和预防策略,已成为当今世界需迫切解决的一个重大问题。国内外诸多学者在这方面也做了大量的研究[6-17]。为了描述易感染细胞、感染细胞以及病毒颗粒之间的关系,在1996年建立了基本的病毒动力学模型[4]:
(1)
其中,x,y,z分别表示健康细胞、感染细胞以及病毒颗粒的数量。健康细胞的产生速率是常数λ,死亡速率为ax,健康细胞被感染的速率为βxz,死亡率为by,病毒颗粒的产生速率为cy,死亡率为dz。
然而考虑到病毒产生时存在时滞,并且对于细胞的感染率多考虑的是双线性函数,因此,文献[6]建立了时滞动力学模型:
(2)
其中,τ表示受感染细胞释放出病毒的时间,其他参数与模型(1)有相同的含义。
要为病毒感染提供更精确的模型,必须考虑免疫应答。因为病毒感染后,机体会产生控制或者消除疾病的免疫应答。当病毒进入易被感染的细胞后,机体中的巨噬细胞等会首先起作用杀死病毒,然后是CTL免疫细胞和抗体起作用,CTL免疫细胞的作用至关重要。因此,在研究病毒感染的模型中引入免疫应答项是非常必要的[11-17]。文献[15]研究了一类具免疫应答和非线性感染函数的时滞HIV感染模型的全局稳定性,在模型中引入了概率。文献[16]建立了具有免疫反应的时滞HIV模型:
该模型得出免疫时滞能影响模型的动力学性态,随着时滞的增大,稳定性开关发生,周期解出现。随着时滞的进一步增大,出现一系列Hopf分支,最终使得正平衡点不稳定。文献[17]提出模型:
说明了时滞对正平衡点稳定性的影响。本文在文献[6,16-17]的启发下,研究具有CTL免疫应答的动力学模型:
(3)
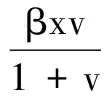
1 基本性质
假设系统(3)的初值为x0=x(0)>0,y0=y(0)≥0,v0=v(0)≥0,z0=z(0)≥0,根据泛函微分方程的基本理论,系统(3)的所有解都是非负的,且是有界的。即有如下的结论:
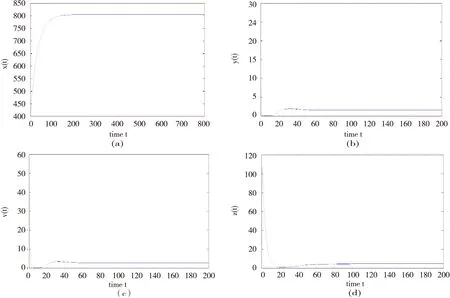
定理1在上述初始条件下,系统(3)的所有解都是非负的,并且一致有界,即存在M>0使得x(t) 证明解由系统(3)的每一个方程得: 显然x(t)>0,z(t)≥0,若y(t)>0,则有v(t)>0成立。 证明系统(3)在E*处的线性化方程组为: 因此,系统(3)在E*处的特征方程为: λ4+a1λ3+a2λ2+a3λ+a4=0 其中, (A+B+μ)(μA+μB+AB+M-N)- μAB+aN-M(μ+B)= μA2+μB2+μ2A+μ2B+A2B+AB2+ 2μAB+AM-(A+B+μ)N+aN 又 μA-N= 于是有μ2A-μN>0,μA2-AN>0,μAB-BN>0成立,所以a1a2-a3>0,且 (A+B+μ)[μA+μB+AB+M-N]· [μAB-aN+(μ+B)M]- [μAB-aN+(μ+B)M]2-(A+B+μ)2μBM= (A+B+μ)AB(μAB-aN)+ μB(μAB-aN)(μ+B)+ (μA-N)MB(A+B)+MAB3+ (μA-N)μM(A+μ)+ (μA-N)(μAB-aN)(A+μ)+ MμAN+(μA-N)μAB2+AM(μAB-aN)+ MA2B2+aBMN+μAM2+ABM2+(B-a)aN2 所以由Routh-Hurwitz定理得,系统(3)在E*处的特征方程的所有根都具有负实部,故平衡点E*局部渐近稳定。 给定参数s=25,a=0.03,β=0.001 445 3,b=0.32,p=0.05,c=3.2,μ=1.8,q=0.2,k=0.3。 图1数值模拟图 从图1形可知,模拟结果与定理2的理论结果一致。该系统的轨迹倾向于感染免疫平衡点E*=(805.12,1.5,2.67,4.88),也就是在这种情况下,病毒感染是慢性的,但同时免疫应答是持久的。 [1] 李益群,李建全,李琳.一类具有CTL作用的HIV感染模型的全局稳定性[J].生物数学学报,2013,28(3):467-472. [2]CUIFANGLV,LIHonghuang,ZHAOHuiyuan.GlobalstabilityforanHIV-1infectionmodelwithBeddington-DeAngelisincidencerateandCTLimmuneresponse[J].CommunNonlinearSciNumerSimulat2014,19(1):121-127. [3]HUANGDongwei,ZHANGXiao,GUOYongfeng,etal.AnalysisofanHIVinfectionmodelwithtreatmentsanddelayedimmuneresponse[J].AppliedMathematicalModelling,2016,40(4):3081-3089. [4]NOWAKMA,BONHOEFFERS,HILLAM,etal.ViralDynamicsinhepatitisBvirusinfection[J].ProceedingsoftheNationalacademyofSciencesoftheUnitedStatesofAmerica,1996,93(9):4398-4402. [5] 眭鑫,刘贤宁,周林.具有潜伏细胞和CTL免疫反应的HIV模型的稳定性分析[J].西南大学学报:自然科学版,2012,34(5):23-27. [6] 郑重武,张凤琴.一类具有感染时滞的HIV模型的稳定性分析[J].数学的实践与认识,2010,40(13):247-252. [7]ELAIWAM,AZOZSA.GlobalpropertiesofaclassofHIVinfectionmodelswithBeddington-DeAngelisfunctionalresponse[J].MathematicalMetheodsintheAppliedSciences,2013,36(4):779-794. [8]KOROBEINIKOVA.Globalpropertiesofbasicvirusdynamicsmodels[J].BulletinofMathematicalBiology,2014,66(4):879-883. [9] 张少辉,靳祯.具有非线性发生率的传染病模型性态分析[J].中北大学学报:自然科学版,2012,33(4):353-357. [10] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004. [11]WANGXia,AHMEDE,SONGXinyu.GlobalpropertiesofadelayedHIVinfectionmodelwithCTLimmuneresponse[J].AppliedMathematicsandComputation,2012,218(18):9405-9414. [12]TIANXiaohong,XURui.GlobalstabilityandHopfbifurcationofanHIV-1infectionmodelwithsaturationincidenceanddelayedCTLimmuneresponse[J].AppliedMathematicsandComputation,2014,237(15):146-154. [13] 李素梅,罗勇,胡亦郑.一类考虑CTL免疫反应的病毒动力学模型的定性分析[J].生物数学学报,2013,28(1):164-168. [14] 陈利君,胡志兴,廖福成.时滞和细胞免疫的HIV-1模型稳定性分析[J].扬州大学学报:自然科学版,2015,18(4):19-23. [15] 常侠,袁朝晖.一类具免疫应答和非线性感染函数的时滞HIV-1感染模型的全局稳定性[J].经济数学,2011,28(4):1-5. [16] 陈美玲.具免疫应答的时滞HIV感染模型动力学性质研究[D].衡阳:南华大学,2010. [17] 曹艳红.具有免疫应答和细胞内部时滞的HIV感染模型的稳定性分析[D].衡阳:南华大学,2011. StabilityofaHIVInfectionModelwithImmuneResponse TIAN Haiyan, GUO Jianmin, GUO Caixia (SchoolofMathematicsandComputerScience,DatongUniversity,Datong037009,China) AHIVmodelwithHollingⅡinfectionrateandimmuneresponseisbuilt.Thenthenonnegativityandboundednessofthesolutionarediscussed,andthebasicreproductionnumberwhichdeterminesthedynamicalbehaviorsoftheinfectionmodelisobtained.Finally,byanalyzingcorrespondingcharacteristicequationatthepositiveequilibrium,itisproventhatthepositiveequilibriumislocallyasymptoticallystable.Thatis,HumanImmunodeficiencyVirus(HIV)persistsinbodyoftheinfectedindividuals,andnumericalsimulationsarecarriedouttosupporttheresult. virusinfection;stability;immuneresponse;positiveequilibrium 2016-03-07 国家青年科学基金项目(11301312);山西大同大学青年科学基金项目(2014Q10;2015K5) 田海燕(1984-),女,山西朔州人,助教,硕士,主要从事微分方程方面的研究,(E-mail)tianhaiyan668@163.com 1673-1549(2016)03-0096-05 10.11863/j.suse.2016.03.20 O175 A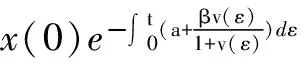
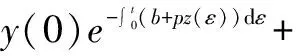
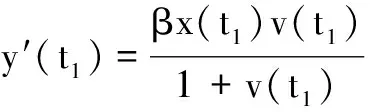
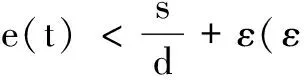
2 正平衡点的稳定性分析
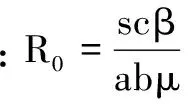
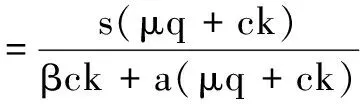
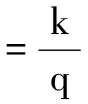
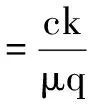
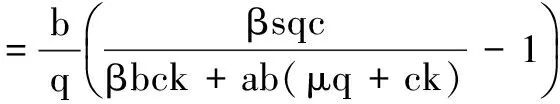
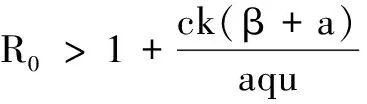
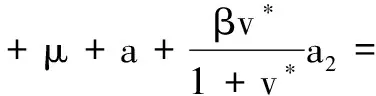
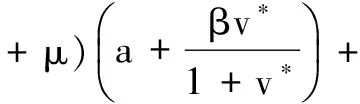
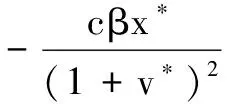
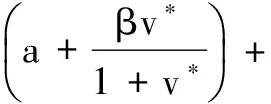
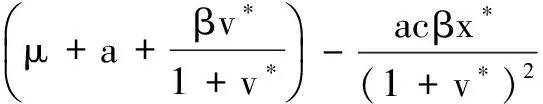
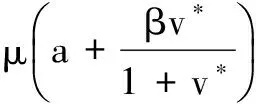
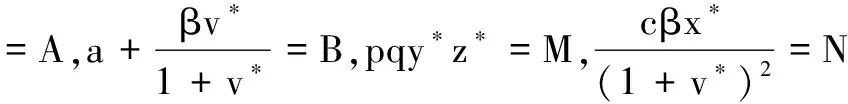
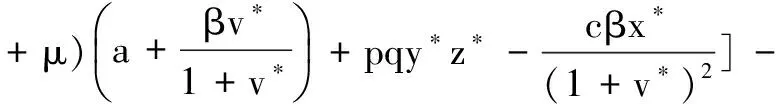
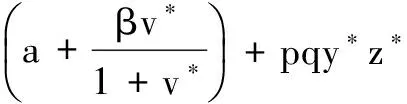
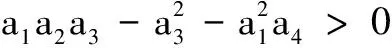
3 数值模拟
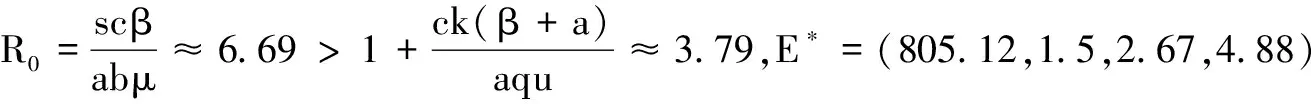
4 结束语