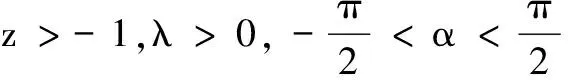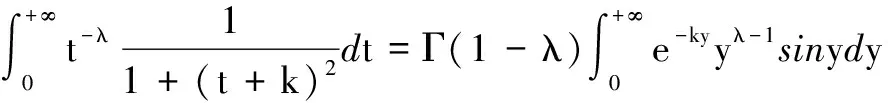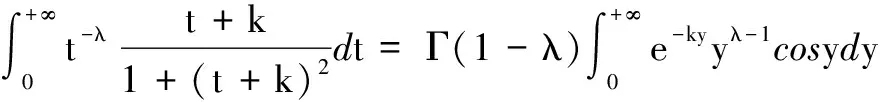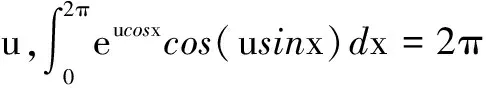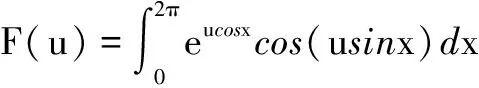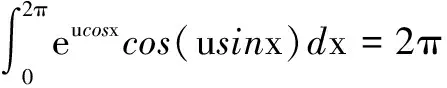广义菲涅尔积分的积分交换次序计算方法

邢家省， 杨小远

(1.北京航空航天大学数学与系统科学学院， 北京　100191；2.数学、信息与行为教育部重点实验室， 北京　100191)



广义菲涅尔积分的积分交换次序计算方法

邢家省1，2， 杨小远1，2

(1.北京航空航天大学数学与系统科学学院， 北京100191；2.数学、信息与行为教育部重点实验室， 北京100191)

考虑两无穷区间上积分交换次序定理的充分条件，经典定理的充分条件要求函数在二重无界区域上绝对可积，这个条件太强，将经典的二重广义积分的绝对可积条件换成积分的内闭一致收敛性条件，得到数学分析中应有的广泛条件下的两积分交换次序结果。利用广泛条件下的两积分交换次序定理，对广义菲涅尔积分计算中的积分可交换次序给出了一般性证明方法，统一了相关广义积分的计算问题，沟通了不同方法之间的内在联系，给出的方法简单直接。

菲涅尔积分；广义菲涅尔积分；含参变量广义积分；内闭一致收敛性；两无穷区间上的积分交换次序定理

两无穷区间上的积分交换次序定理[1-12]是数学分析中的重要经典结果，文献[1-8，12]给出了两无穷区间上积分可交换积分次序的充分条件和证明过程。然而此经典定理在使用中非常不方便，对许多二元函数实施积分交换次序时不能直接套用，有时只能间接的在两任意内部区间上套用[2,5,7-10]，然后再通过对变动区间上的积分取极限[2,5,7-10]。经典定理的充分条件要求二元函数在二重无界区域上绝对可积[1-8]，这个条件也相当苛刻，一些常见函数也不满足此条件，也只能间接使用，然后采用其他复杂的解决办法[2,5,7-10]。这就必然导致要对经典的积分交换次序条件进行改进[2,5,7-14]，在广泛的充分条件下给出积分交换次序定理的结果，得到数学分析中最好的理论表现形式，并且在导出好的结果的过程中完全是利用数学分析自身已有的理论方法，利用新的表述结果可以更方便于解决一批函数的积分计算问题。以理论先进的形式传播，达到数学分析学中应有的理论高度，构成一般性的处理方法。

1　无穷区间上积分交换次序定理的经典充分条件及其局限性

定理1[1-7](无穷区间的积分交换次序)设函数f(x,u)在[a,+∞)×[α,+∞)上连续，如果满足下列条件：

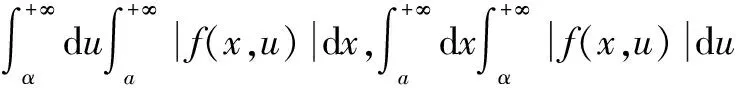
定理1是标准数学分析中的经典结果，文献[1-7]中对定理1的叙述和证明过程都是此条件。定理1中充分条件(1)是包含端点的半内闭一致收敛性条件，这是不必要的，完全可以改为不含端点的真正内闭一致收敛性条件；定理1的条件(2)是二元函数在无界区域上的绝对可积条件，此条件相当苛刻，对许多函数不能直接套用此定理。在内部区间上间接的使用[2,5,7-8]，然后采用再取极限的办法，这是相当繁琐的。可以将定理1中的条件(1)和条件(2)改进为一般形式，得到好的一般结果形式，新的结果更方便于使用。

2　函数列积分的极限理论结果

定理2[1-4]设{fn(x)}是[a,b]上的黎曼可积函数列，如果{fn(x)}在[a,b]上一致收敛于f(x)。则有：

(1)f(x)在[a,b]上黎曼可积；

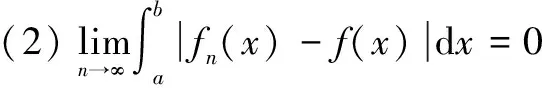
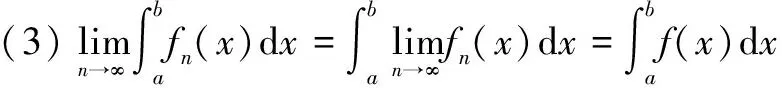
定理3[1-4]设{fn(x)}是[a,b]上的连续函数列，如果{fn(x)}在[a,b]上一致收敛于f(x)。则有：

(1)f(x)在[a,b]上连续；

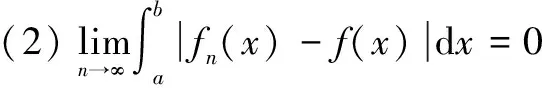
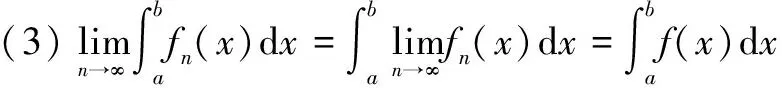
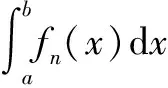
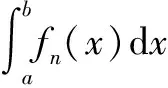
定理4的区间(a,b)可为有限区间，也可为无限区间。定理4常被使用的情形是控制收敛定理。

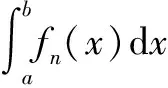
如果满足：

(1)对任意b>B>A>a，{fn(x)}在[A,B]上一致收敛于f(x)；

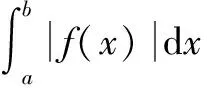
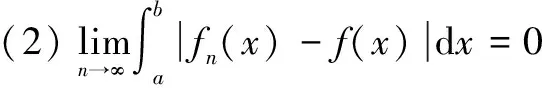
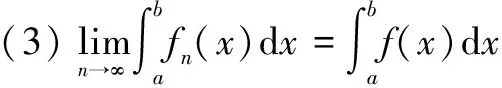
定理5的区间(a,b)可为有限区间，也可为无限区间。

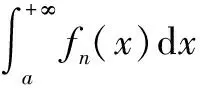
如果满足：

(1)对任意B>A>a，{fn(x)}在[A,B]上一致收敛于f(x)；

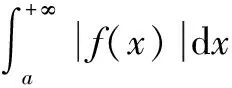
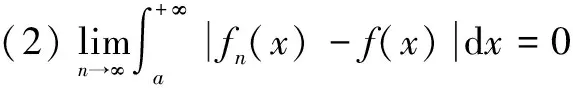
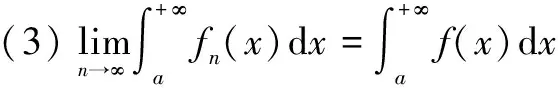
定理4、5、6虽然是以函数列的极限形式叙述的，但完全可以写出其他极限形式的相应结论[1-4]。

3　无穷区间上积分交换次序的充分条件的改进结果

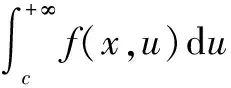
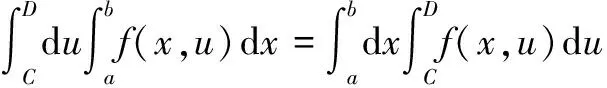
结论得证。

定理8设函数f(x,u)在[a,b]×(c,+∞)上连续，如果满足条件：

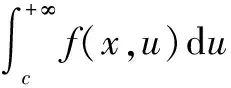
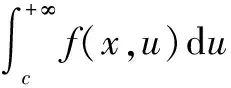
定理9设函数f(x,u)在[a,b]×(c,+∞)上连续，如果满足条件：

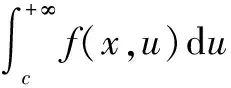
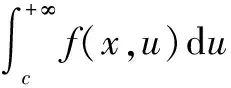
定理10设函数f(x,u)在[a,b]×(c,+∞)上连续，如果满足条件：

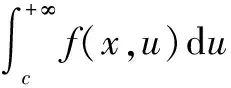
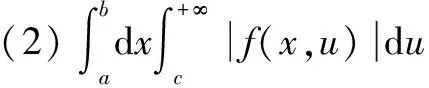
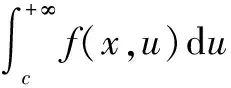
定理11(无穷区间上的积分交换次序)设函数f(x,u)在(a,+∞)×(c,+∞)上连续，如果满足下列条件：

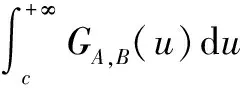
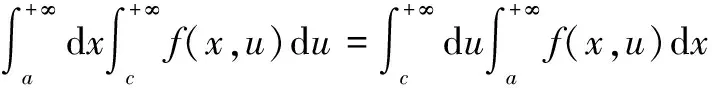
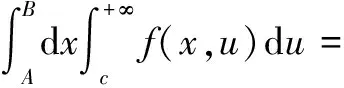
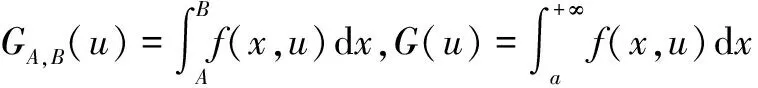
从而

故

定理12[8,12](无穷区间上的积分交换次序)设函数f(x,u)在(a,+∞)×(c,+∞)上连续，如果满足下列条件：

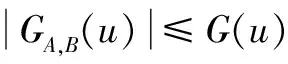
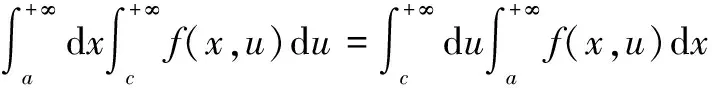
显然定理11和定理12的条件比定理1的条件广泛自然，也就是定理11和定理12的结果优于定理1的结果，应该采用定理11或者定理12去替代定理1，数学分析中的积分交换次序定理应该以定理11或定理12的结果为最终形式，此结果完全是利用数学分析自身已有的理论方法，证明过程没有增加任何困难。定理11或定理12的充分条件，在实际应用中非常方便于验证，减少了解决问题的难度，使用范围广泛。定理11或定理12的结果，达到了数学分析中应有的理论高度。

一般地，对(a,b)×(c,d)上的积分交换次序定理的充分条件类似的可以给出，这里下限a,c可以是有限的或为-∞，上限b,d可以是有限的或为+∞。

4　Dirichlet积分的简便计算方法

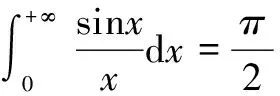
(1)

需证明成立：

(2)

在(2)式成立的情况下，可得到

(3)

故

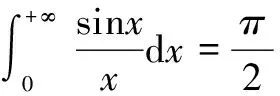
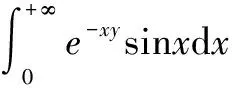
(4)

在(4)式两端，令b→+∞，取极限，则得

(5)

在(5)式两端，令a→0+，取极限，则得(2)式成立。

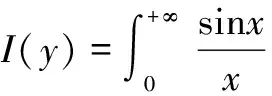
5　广义菲涅尔积分计算中的积分交换次序的一般方法

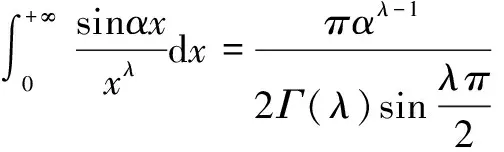
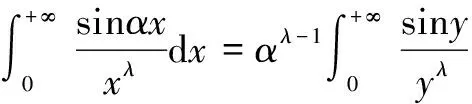
(6)

可以证明成立[2,5-7]：

(7)

在(7)式成立的情况下，可得

故有

其中利用了贝塔函数的性质[1-3]和Γ函数的余元公式[1-3]。

证明(7)式成立：

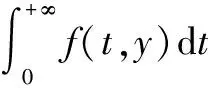
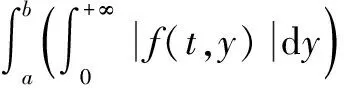
(8)

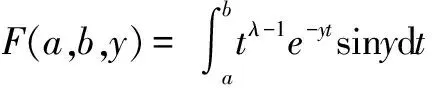
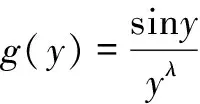
H(a,y)-H(b,y)

F(a,b,y)=g(y)H(a,y)-g(y)H(b,y)

利用黎曼积分下的积分收敛定理，于是有

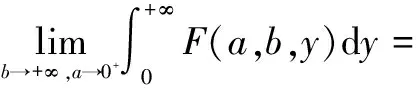
在(8)式两端令b→+∞,a→0+，取极限，得到成立

故(7)式得证。

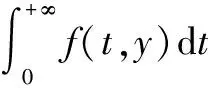
(9)

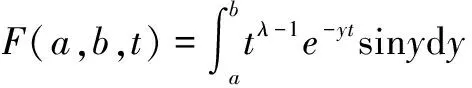
注意到

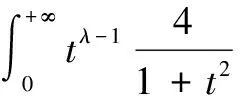
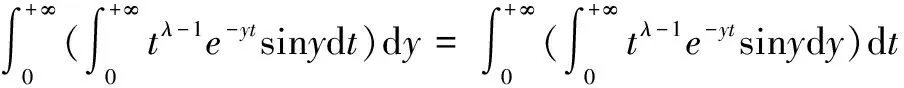
利用定理14的结果，可以再次得到

定理15[2,5-7]设0<λ<1，则有

证明利用分部积分和定理14的结果，得

定理16[2,5-7]设p>1，则有

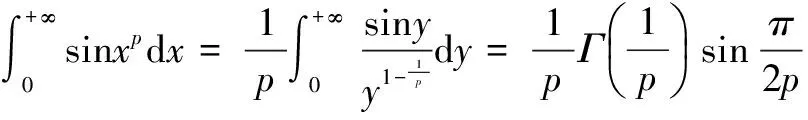
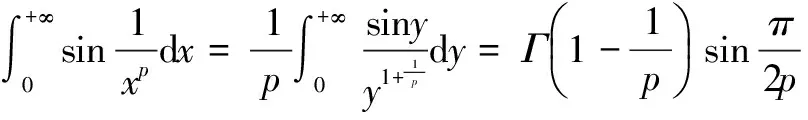
用类似于证明(7)式的方法，同理可证成立

(10)

利用(10)式，可以得到：

定理17[2,5-7]设α>0,0<λ<1，则有

定理18[2,5-7]设p>1，则有

6　一类Euler积分公式及其应用

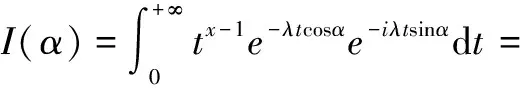
从而

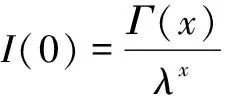
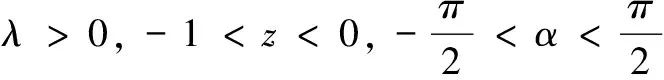
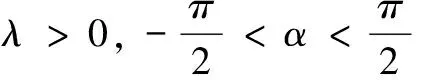
x∈[0,1]

对-1

λcos(λtsinα)sinα]dt=

定理20的结果得证。

定理22[2,15]设k>0,-1<λ<1，则有

(11)

(12)

用类似于证明(7)式的方法，可以证明成立：

(13)

于是

在

于是

定理23[2,15]设k>0,0<λ<1，则有

(14)

利用(14)式，可得

并利用Euler公式

(sinα)λΓ(λ)cosλα

于是，

Γ(1-λ)Γ(λ)(sinα)λcosλα=

F(0)=2π

sin(usinx)sinx]dx=

[1] 常庚哲,史济怀.数学分析教程(下册)[M].北京:高等教育出版社,2003.

[2] 黄玉民,李成章.数学分析(下册)[M].2版.北京:科学出版社,2007.

[3] 华罗庚,著.王元,校.高等数学引论(第二册)[M].北京:科学出版社,2009.

[4] 张筑生.数学分析新讲(第三册)[M].北京:北京大学出版社,1990.

[5] 费定晖,周学圣.吉米多维奇数学分析习题集题解(五)[M].济南:山东科学技术出版社,1980.

[6] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2002.

[7] 匡继昌.实分析与泛函分析续论(上册)[M].北京:高等教育出版社,2015.

[8] 白玉兰,陈述涛.一个二次广义积分的顺序交换问题[J].哈尔滨师范大学学报:自然科学版,1987,3(3):13-18.

[9] 姜赞臣.含参变量无穷积分在积分号下可积分定理的推广[J].淄博师专学报,1995(2):15-17.

[10] 匡继昌.Dirichlet积分九种解法的思路分析[J].高等数学研究,2012,15(4):61-64.

[11] 许宁.Dirichlet积分及其应用[J].高等数学研究,2014,17(3):15-19.

[12] 邢家省,杨小远,白璐.两无穷区间上积分交换次序充分条件的改进及其应用[J].四川理工学院学报:自然科学版,2016,29(1):87-92.

[13]FLANDERSH.OntheFresnelIntegrals[J].TheAmericanMath.Monthly,1982,89(4):264-266.

[14]LEONARDIE.MoreonFresnelIntegrals[J].TheAmericanMath.Monthly,1988,95(5):431-433.

[15] 华罗庚,著.王元,校.高等数学引论(第三册)[M].北京:科学出版社,2009.

CalculationofIntegralsExchangeofGeneralizedFresnelIntegrals

XING Jiasheng, YANG Xiaoyuan

(1.SchoolofMathematicsandSystemsScience,BeihangUniversity,Beijing200191,China;2.LMIBoftheMinistryofEducation,BeihangUniversity,Beijing100191,China)

Consideredthesufficientconditionofexchangetheoremofintegralsequencewithintwoinfiniteinterval,sufficientconditionofclassicaltheoryisverystrongwhichrequirefunctionabsolutelyintegrableintwiceunboundedintervals.Iftheabsolutelyintegrableconditionofclassictwiceintegralintointernaluniformconvergenceofintegralischanged,theresultoftwiceintegralexchangingsequencewithinreasonablegeneralizedconditionofmathematicalanalysisisgained.Usedtheexchangetheoremofintegralsequencewithinthegeneralizedcondition,thegeneralproofofintegralsexchangeofthegeneralizedFresnelintegralwhichunifythecalculationofgeneralizedintegralsisgiven.Furthermore,thismethodcanimprovetheefficiencyofcalculation.

Fresnelintegrals;generalizedFresnelintegrals;generalizedintegralcontainedparameters;innercloseuniformlyconvergence;integralsexchangetheoremoninfiniteinterval

2015-11-22

国家自然科学基金资助项目(61271010)；北京航空航天大学校级重大教改项目(201401)

邢家省(1964-)，男，河南泌阳人，副教授，博士，主要从事偏微分方程、微分几何方面的研究，(E-mail)xjsh@buaa.edu.cn;

杨小远(1964-)，女，辽宁沈阳人，教授，博导，主要从事应用调和分析、图像处理方面的研究，(E-mail)xiaoyuanyang@buaa.edu.cn

1673-1549(2016)03-0085-08

10.11863/j.suse.2016.03.18

O177.2

A