预应力混凝土结构收缩与徐变损失的计算分析与有限元模拟研究

黄　颖， 高　杰

(福建船政交通职业学院， 福州　350007)



预应力混凝土结构收缩与徐变损失的计算分析与有限元模拟研究

黄颖， 高杰

(福建船政交通职业学院， 福州350007)

在结构施工和使用过程中，混凝土的收缩和徐变对结构的变形和内力均有巨大的影响，也是造成预应力混凝土梁桥预应力损失的一个重要因素。采用基于位移法的初应变法结合有限元对预应力混凝土结构中的收缩与徐变进行分析，建立了收缩与徐变的时步分析方法。此方法能得到每一个时间步的内力改变量，将前一个荷载步的内力与此内力改变量叠加，将混凝土收缩徐变损失与钢筋松弛损失有机结合起来，而不是单纯的将两种损失进行叠加分析。通过算例分析得出：混凝土收缩徐变在加载初期挠度增量变化快，经过一段时间后逐渐趋于稳定，第一年内收缩徐变损失值占20年收缩徐变总量的60%，跨中截面挠度值约占20年时刻总挠度的80%。

预应力混凝土；预应力损失；收缩；徐变；时步分析

引　言

在结构施工和使用过程中，混凝土的收缩和徐变对结构的变形和内力均有巨大的影响，也是造成预应力混凝土梁桥预应力损失的一个重要因素，因此，如何较为精确的计算结构的收缩和徐变值对结构的性能分析是十分重要的。国内外工程师进行了广泛的研究：从20世纪30年代由DISchinger F提出的混凝土徐变收缩微分方程求解法，改进的Dishcinger法，逐步发展到有效模量法以及按龄期调整的有效模量法[1-2]等。各国规范也分别提出了收缩徐变的计算模型，包括国际预应力协会(FIP)提出的CEB-FIP78模型、欧洲混凝土委员会(CEB)提出的CEB-FIP90[3]模型、美国混凝土协会209委员会提出的ACI209模型[4]、澳大利亚AS3600规范[5]提出的收缩徐变模型，这些模型中都体现了收缩徐变与时间的关系，也就是预应力混凝土的收缩徐变具有随着时间变化的特性。近年来，随着计算机技术的不断发展，预应力混凝土收缩徐变效应逐渐被工程界重视，产生了不少研究成果[6-13]。

目前主要采用的徐变计算理论主要有：按照龄期调整的有效弹性模量法和初应变法。从已有的研究可知，大部分的研究都集中在采用有效弹性模量法对预应力混凝土结构收缩徐变损失进行分析，大都以徐变与应力的线性关系为依据[14-15]。按照龄期调整的有效弹性模量法在单独分析预应力收缩徐变损失中具有较高的精度[10,12]，但是预应力各长期损失之间不是独立的，混凝土收缩徐变会改变混凝土材性，而混凝土材性的改变又将影响钢筋的松弛，因此必须建立混凝土收缩与徐变的时步分析方法，这样才能将收缩徐变损失和钢筋松弛损失相结合，获得的预应力结构长期损失更加准确，本文采用基于位移法的初应变法结合有限元法进行分析。

1　混凝土收缩与徐变计算方法分析

混凝土徐变计算的初应变法[16]能把徐变计算的复杂问题简化成在每个徐变计算时段内常应力的徐变计算与解弹性内力相结合的简单问题，显然，若时间段取为无限小，计算将是准确的。初应变法能得到每一个时间步的内力改变量，将前一个荷载步的内力与此内力改变量叠加，可以作为钢筋松弛损失计算的依据，这样就可以将混凝土收缩徐变损失与钢筋松弛损失有机结合起来，而不是单纯的将两种损失进行叠加分析。实际计算经验表明，可以用相当大的时间步长而得到适用的计算精度。因此本文采用初应变法对徐变和收缩进行计算分析。

1.1混凝土徐变应变计算

将时间轴上各个时刻t0、t1、…tn、tn+1、…作用的应力增量定义为Δσ0、Δσ1、…、Δσn、Δσn+1、…。考虑在tn时刻，在Δtn+1(tn～tn+1)时间内的情况，单元内任意一点的应力为：

(1)

式(1)反映了在tn时刻之前的应力，在Δtn+1(tn～tn+1)时间内，如果忽略结构的应力和材料常数变化的影响，则徐变增量为：

(2)

式中：D为混凝土的刚度矩阵；Δφ(tj,ti)为加载龄期为ti，计算考虑龄期为ti时的混凝土徐变系数。

(3)

Δσi=D(Δεi-Δε0i)

(4)

其中：Δεi为结点位移引起的应变增量，Δε0i为结点上一时刻的应变增量(包括由温度变化、施工误差、收缩徐变等初应变产生)，BT为应变矩阵。

∫BTΔσidυ=∫BTDΔεidυ-∫BTDΔε0idυ=

(5)

其中：

(6)

ΔRi2=-∫BTDΔε0idυ

(7)

式中：ΔRi1为由结点位移增量引起的杆端力增量，ΔRi2为由Δε0i引起的固端力增量。将式(5)代入式(3)可得：

(8)

利用桥梁规范[17]附录F中给出的徐变系数的计算公式，各参数含义参见文献[17]：

Δφ(tj,ti)=φ0·βc(tj-ti)

(9)

其中：

φ0=φRH·β(fcm)·β(ti)

式中：ti——加载时的混凝土龄期(d)；

tj——计算考虑时刻的混凝土龄期(d)；

Δφ(tj,ti)——加载龄期为ti，计算考虑龄期为ti时的混凝土徐变系数；

φ0——名义徐变系数；

βc——加载后徐变随时间发展的系数。

将公式(9)代入式(8)得到：

(10)

1.2混凝土收缩应变计算

混凝土的收缩应变对结构的影响也可以作为初应变问题进行计算，收缩应变通常采用指数函数曲线[7,18-19]：

εs(t)=εs(∞)(1-e-pt)

(11)

其中：εs(∞)为收缩应变极值；P为收缩应变增长系数。

各单元混凝土的龄期不同，因此收缩计算的起点也就不同，设混凝土的硬化时间为τ0，则：

εs(∞)[e-p(tn-τ0)-e-p(tn+1-τ0)]=

εs(∞)e-p(tn-τ0)(1-e-pΔtn+1)

(12)

则收缩引起的结点荷载为：

(13)

对于等截面杆件单元，单元的收缩应变沿截面的高度方向是一致的，因此所引起的单元等效结点荷载只有单元轴向力N，其增量的绝对值为：

(14)

则单元收缩固端力向量为：

(15)

则由收缩引起的单元等效结点荷载增为：

(16)

2　混凝土收缩与徐变损失的有限元模拟

利用ANSYS对混凝土徐变和收缩进行分析的基本步骤是：首先是输入基本参数，包括单元的基本信息，节点信息，约束信息，材料信息，外荷载等初始参数；确定时间轴，然后进行时步循环，时步循环结束则收缩徐变计算结束。对于时间轴的确定及时步的划分，查阅相关文献可知[20-22]，收缩徐变一般遵循指数函数的规律，因此每个阶段的时间步长可以依据对数函数公式选取：

SM=(lnTe-lnTs)/n

(17)

lnTi+1=lnTi+SM

(18)

其中：SM——时间步长(对数形式)；

Te——收缩徐变计算终了时刻(d)；

Ts——成桥时刻(d)；

n——运营期间计算时间步数

Ti+1、Ti——分别为第i和i+1步长对应的时刻(i=0,1,2,3,…,n)。

其中在时步的每一次循环中又包括7个主要步骤按顺序依次为：

计算梁单元和杆单元的刚度矩阵，形成结构总体刚度矩阵。

计算外荷载，对温度、制造误差、施工误差等初应变按式(7)计算ΔRi2。

计入上一时步的收缩徐变等效结点荷载，同时将其反号叠加至ΔRi2中作为徐变初应变影响部分。

获得结点位移增量。

根据式(6)计算由杆端内力增量ΔRi1。

按式(10)计算下一时步的收缩徐变等效结点荷载。这样即用有限元的方法实现了混凝土的收缩徐变计算。具体流程图如图1所示。

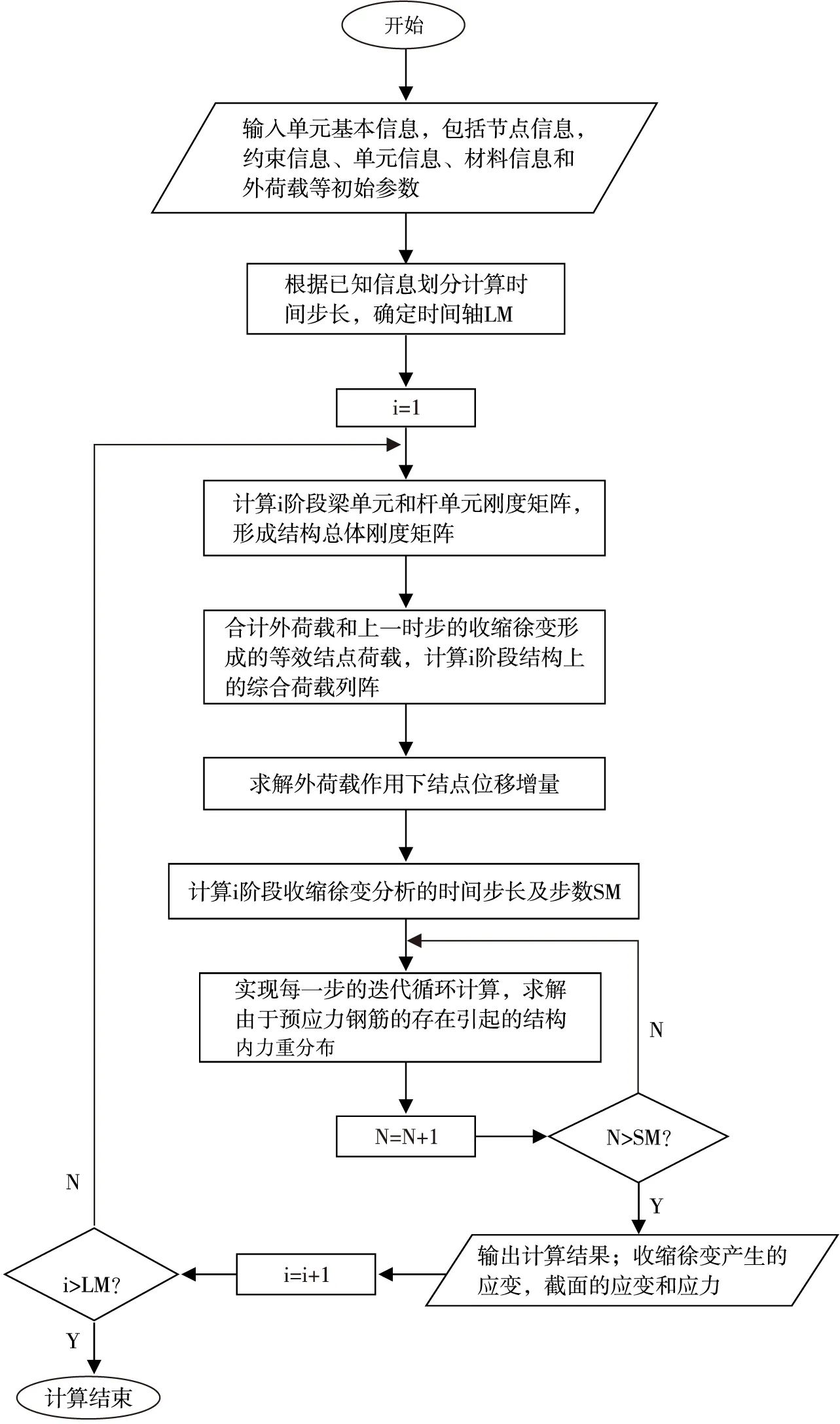
图1混凝土收缩徐变有限元计算流程图

3　混凝土收缩与徐变的时步分析方法

利用有限元分析软件ANSYS，建立模型试验梁的有限元计算模型，如图2所示。梁长16 m，截面高度90 cm，宽度875(550) cm，受拉钢筋和受压钢筋均采用Ф20，箍筋采用Ф8，预应力束采用24ФS5，混凝土设计强度采用C50，预应力钢绞线标准强度采用1600 MPa，模型由22 540个混凝土单元，501单元和3840个钢筋单元组成。试验模型的混凝土为一般养护，以成桥状态为分析基础，结合上述方法，建立收缩与徐变损失的有限元时步分析方法，分析过程中外加荷载对称加载120 kN，施加外荷载龄期为5 d，收缩徐变终了时刻取成桥时刻后的20年(7 d×52 w×20 y)，以7 d作为时间步，则运营期间的计算时间步数为1040。由于数值量较大，在半年内，记录每隔7 d荷载步计算值，半年后，记录每隔0.5 y(y表示年)计算梁体混凝土收缩徐变产生的预应力损失量及对应此刻跨中截面挠度值，数据汇总于表1中，同时绘制收缩徐变随着时间步长的变化曲线及伴随收缩徐变损失梁体跨中截面挠度随着时间步长变化曲线(图3)。从表1数据及图3曲线趋势可以看出，混凝土收缩徐变在加载初期挠度增量变化快，经过一段时间后逐渐趋于稳定，一年内收缩徐变损失值为59.78 MPa，完成量占20年收缩徐变总量的60%，在固定外加荷载的情况下，通过有限元时步计算，当梁体服役了1年时，跨中截面挠度值为35.916 mm，约占20年时刻总挠度的80%。

表1　试验梁收缩徐变损失的有限元时步分析

图2有限元模型三维视图

图3收缩徐变损失分析曲线

4　结　论

本文采用基于位移法的初应变法结合有限元对预应力混凝土结构中的收缩与徐变的计算方法进行分析，同时通过有限元建模对预应力混凝土结构的收缩徐变进行模拟计算，得到以下结论：

(1)建立基于位移法的初应变法把徐变和收缩计算的复杂问题简化成了在每个徐变计算时段内常应力的徐变计算与解弹性内力相结合的简单问题，建立了徐变和收缩的时步分析方法，分析效率提高，并且较为精确地对混凝土收缩徐变损失进行有限元模拟。

(2)基于位移的初应变法能够得到每一个时间步荷载作用下的应力增量、弹性应变增量和徐变应变增量，这样就可以将混凝土收缩徐变损失与钢筋松弛损失计算耦合起来，而不是单纯地将两种损失进行叠加分析，考虑了各损失间的互相影响关系。

(3)通过对试验梁收缩徐变有限元时步分析可知：在服役初期，梁体收缩徐变损失增长较快，经过一段时间后逐渐趋于稳定，梁体在第一年内完成的收缩徐变损失约占20年收缩徐变损失总值的60%。

[1] 项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.

[2] 吴红林,黄侨,土宗林.全时程时效分析理论及其在大跨桥梁长期性能预测中的应用[J].东北公路,2002,25(3):48-52.

[3] CEB-FIP,模式混凝土结构规范[S].

[4] ACI Committee 209(1992),Prediction of creep,shrinkage and temperature effects in concrete structures[S].

[5] AS3600,Australia a Standard for concrete Structures[S].

[6] Bazant Z P,Kim J.Improved predication model for time-dependent deformations of concrete:Part2～Shrinkage[J].Materials and Structures,1991,24:409-421.

[7] Bazant Z R.Prediction of concrete creep and shrinkage:past,present and future[J].Nuelear Engineering and Design,2001,203:27-38.

[8] 项贻强,何晓阳.考虑非均匀收缩徐变的PC箱梁桥时变性能[J].哈尔滨工业大学学报,2015,47(12):117-122.

[9] 刘沐宇,卢志芳.混凝土桥梁时变性和不确定性下的收缩徐变分析[J].华中科技大学学报:自然科学版,2011,39(10):116-120.

[10] 苏成,陈兆栓,徐郁峰,等.预应力混凝土斜拉桥收缩徐变效应的概率分析[J].华南理工大学学报:自然科学版,2012,40(7):8-14.

[11] 方坚宇,马吉倩.收缩徐变对简支变连续结构受力性能影响研究[J].公路,2012(11):171-176.

[12] 黄海东,向中富,郑皆连.PC箱梁桥三维徐变效应精细化分析[J].中国公路学报,2013,26(5):108-114.

[13] 卢志芳.考虑时变性和不确定性的混凝土桥梁收缩徐变及预应力损失计算方法[D].武汉:武汉理工大学,2011.

[14] 侯宁.自锚式悬索桥混凝土收缩徐变效应研究[D].长安:长安大学,2011.

[15] 薛伟辰,胡于明,王巍.预应力混凝土梁徐变性能试验[J].中国公路学报,2008,27(4):61-66.

[16] 朱伯芳.有限单元法原理及应用[M].北京:水利电力出版社,1979.

[17] JTGD62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[18] 杨小兵.混凝土收缩徐变预测模型研究[D].武汉:武汉大学,2004.

[19] 丁文胜,吕志涛,孟少平,等.混凝土收缩徐变预测模型的分析比较[J].桥梁建设，2004(6):13-16.

[20] 颜东煌,田仲初.混凝土桥梁收缩徐变计算的有限元方法与应用[J].中国公路学报,2004,17(2):55-58.

[21] 黄侨,吴红林,王宗林.基于时效分析理论的预应力混凝土结构分析[J].同济大学学报,2003,31(7):813-818.

[22] 潘钻峰,吕志涛,刘钊.考虑收缩、徐变和松弛相互影响的预应力长期损失计算[J].现代交通科技,2010,7(5):15-17,30.

Computational Analysis and Finite Element Simulation Study on Shrinkage and Creep of Prestressed Concrete Structures

HUANGYing,GAOJie

(Fujian Chuanzheng Communications College, Fuzhou 350007, China)

In the process of construction and service, the shrinkage and creep of concrete have great influence on the deformation and internal force of the structure, and are also important factors that cause the loss of the prestressed concrete beam bridge. The time step analysis method of shrinkage and creep was established through combining the initial strain method based on displacement method with the finite element method. This method could get the change of the internal force of each time step, and the internal force of the previous load step was added to the change of the internal force. The shrinkage and creep of concrete were combined with the relaxation loss of the steel, rather than the two loss of superposition analysis. Through the example analysis, this paper concluded that the concrete shrinkage and creep deflection incremental changed faster in the initial loading, and gradually stabilized after a period of time. The shrinkage and creep loss value accounted for 60% of the total shrinkage and creep of 20 years, and the cross section deflection value accounted for about 80% of the total deflection of 20 years after one year.

prestressed concrete; prestress loss; shrinkage; creep; time-stepping analysis

2016-03-07

福建省交通厅交通科技项目(201336)；福建省教育厅科技项目(JA15664)

黄 颖(1982-)，女，福建福州人，讲师，博士，主要从事预应力结构动力性能与耐久性方面的研究，(E-mail)huangying6820@163.com

1673-1549(2016)03-0075-05

10.11863/j.suse.2016.03.16

TU311.3

A