基于时温等效原理的热致形状记忆聚合物模型

张泽斌, 阚前华, 董诗玉, 李　建, 康国政

(1.应用力学与结构安全四川省重点实验室, 成都　610031;2.西南交通大学力学与工程学院, 成都　610031)



基于时温等效原理的热致形状记忆聚合物模型

张泽斌1,2, 阚前华1,2, 董诗玉1,2, 李建1,2, 康国政1,2

(1.应用力学与结构安全四川省重点实验室, 成都610031;2.西南交通大学力学与工程学院, 成都610031)

基于粘弹性高分子理论和时温等效原理，对玻璃态热致型形状记忆聚合物的形状记忆过程进行模拟。将形状记忆聚合物的粘弹性应力应变响应分为依赖于应变的应力部分和依赖于时间的松弛部分。依赖于应变的应力部分采用不可压缩的Mooney-Rivlin超弹性模型，依赖于时间的松弛部分采用Prony级数表示。通过新的时温等效方程来考虑模量的温度相关性。模拟结果与实验的比较表明：模拟结果与实验吻合很好。

形状记忆聚合物；粘弹性；超弹性；时温等效

引　言

形状记忆聚合物(SMP)是继形状记忆合金之后发展起来的又一新型形状记忆材料，在新型医疗设备、智能主动控制结构和可折叠结构等领域中获得广泛重视和应用[1]。形状记忆聚合物可分为热致感应型、光致感应型和化学感应型形状记忆聚合物，其中热致型形状记忆聚合物由于设计简单和容易控制已成为目前形状记忆聚合物研究和开发的最活跃的材料。热致型形状记忆聚合物可看作是两相结构，即在形状记忆过程中保持固定形状的固定相和随温度变化能可逆地固化和软化的可逆相组成。形状聚合物的形状记忆共包括“记忆起始态→固定变形态→回复到起始态”的四个过程[2]。

SMP热力学模型方面的研究也是近年来的热点研究之一，取得了一系列成果。Tobushi等[3]根据传统粘弹性理论引入不可恢复的滑移单元建立了一维线性本构模型。随后，Tobushi等[4]在此基础上，构建了能描述SMP热力学行为的一维非线性本构模型。Liu等[5]认为SMP由高温软化相和低温冻结相组成，形状记忆效应是在温度变化和应力共同作用，建立了描述SMP热力学行为的细观力学三维本构模型。李郑发等[6]借鉴聚合物结晶学的相关理论，建立了描述SMP力学行为的微观三维本构模型，解释了SMP的微观机理。周博等[7]基于弹性应变、非弹性应变、粘性应变和热应变分解建立热粘弹塑性模型。Baghani等[8]基于传统的热力框架和Henchy应变提出了大应变情况下的宏观三维本构模型。Guo等[9]基于粘弹性理论和相变理论，将应变分为弹性应变、粘弹性应变和热膨胀应变，建立了三维本构模型。

虽然关于SMP的热力学本构模型研究已经有了很多进展，但由于SMP的形状记忆机理比较复杂，本构模型构造较为麻烦，且非线性本构方程的求解难度较大，所以目前仍然没有有效模型和求解方法来模拟SMP的形状记忆过程。本文通过粘弹性高分子理论结合时温等效原理对热致形状记忆聚合物的形状记忆过程进行模拟。

1　本构模型

1.1粘弹性应力描述

将形状记忆聚合物的粘弹性应力响应σ分为两部分：依赖于应变的应力部分σ0(ε)和依赖于时间的松弛部分g(t)，并假定为乘积关系：

σ(ε,t)=σ0(ε)·g(t)

(1)

其中，σ0(ε)采用不可压缩Mooney-Rivlin超弹性模型[10]进行描述：

σ0(ε)=2[(1+ε)-(1+ε)-2][C10+

(1+ε)-1C01]

(2)

其中，C10、C01为材料常数。时间松弛部分g(t)可用Prony级数表示为:

(3)

(4)

其中，g∞和gi为无量纲化的常数。σ0(ε)表示初始时刻材料的应力-应变关系，g∞σ0(ε)表示松弛达到平衡时材料的应力-应变关系。

1.2时温等效方程

当进行与温度相关的粘弹性分析时，需要不同温度下的松弛模量，在实验中可以在不同时间区间内进行聚合物的松弛试验，利用时间-温度等效原理，得出完整的模量随时间变化的情况，用公式(5)表示[11]：

E(T1,t)=E(T2,t/aT)

(5)

该式表明改变温度的效应等同于在时间尺度上除以移位因子aT。

2　模型预测结果

2.1材料参数

形状记忆聚合物的基本材料参数可从文献[3]获取。通过式(6)拟合在参考温度T0下的剪切松弛模量实验曲线：

(6)

材料的松弛数据见表1。

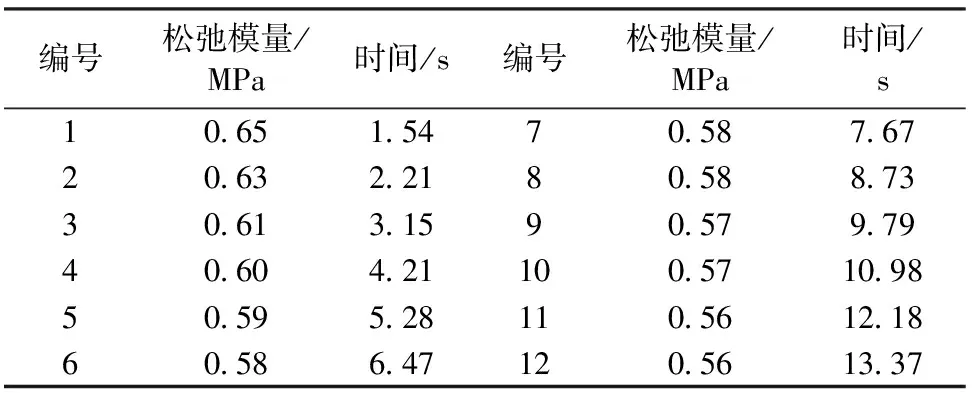
表1　材料剪切松弛模量与松弛时间

根据Tobushi[3]的实验结果，对不同温度下的应力松弛实验结果进行整理，根据公式(5)，计算出不同温度T下移动因子aT值，对时温等效方程进行拟合，得到如下多项式标识的移位因子表达式：

(7)

其中：T0为参考温度，A0、A1、A2、A3和A4为系数，其值见表2。公式(7)可通过用户子程序UTRS嵌入到ABAQUS中，实现对时温等效方程的调用。

Mooney-Rivlin超弹性模型中参数的确定方法为：(1)首先采用弹性模型对形状记忆过程进行模拟，弹性模量E=907 MPa，然后与最大应变ε=4%的实验工况进行对比，不断修正最初输入的弹性模量E，直到与实验结果吻合程度较高；(2)采用Mooney-Rivlin超弹性模型对模拟数据进行拟合，确定出C10与C01值。

模拟中的使用的材料参数见表2。

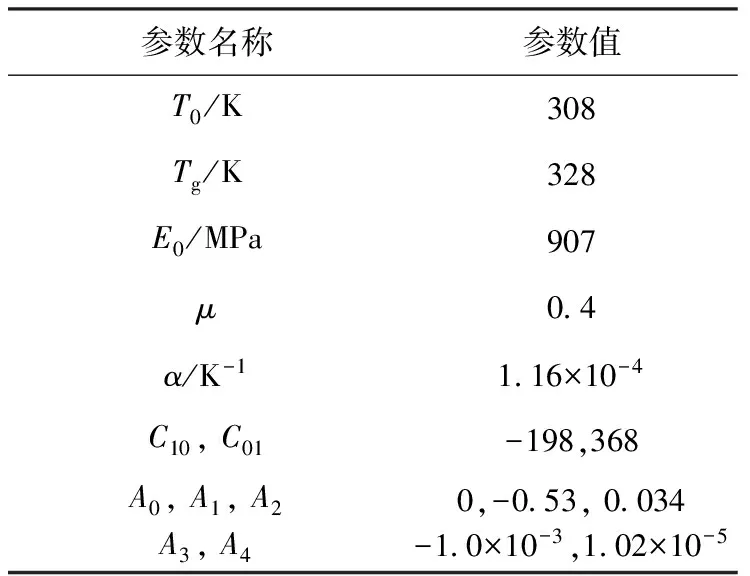
表2　材料参数

2.2加载过程

根据形状记忆的过程，将其分为四个步骤：

(1)高温时，对SMP进行单调拉伸的位移加载；(2)加载完毕后，对SMP降温，此时保持试件位移加载应变不变；(3)保持低温载荷不变，卸载位移约束；(4)对SMP加温，SMP形状回复至原始形状。

根据文献[3]提供的实验加载条件，应变加载率为50 %/min，升降温速率为8 K/min。

2.3模拟结果

图1为不同应变下实验和模拟的应力-应变曲线，从图中可以得出：在高温加载阶段(第1阶段)，随着应力的增加应变表现出非线性的增加；在降温阶段(第2阶段)，保持应变不发生变化，弹性模量逐渐变大，应力也随着增加；在卸载阶段(第3阶段)产生了少量恢复变形；在升温阶段(第4阶段)，应变随着温度的增加发生恢复。不同峰值真应变下的模拟结果和试验结果吻合很好。

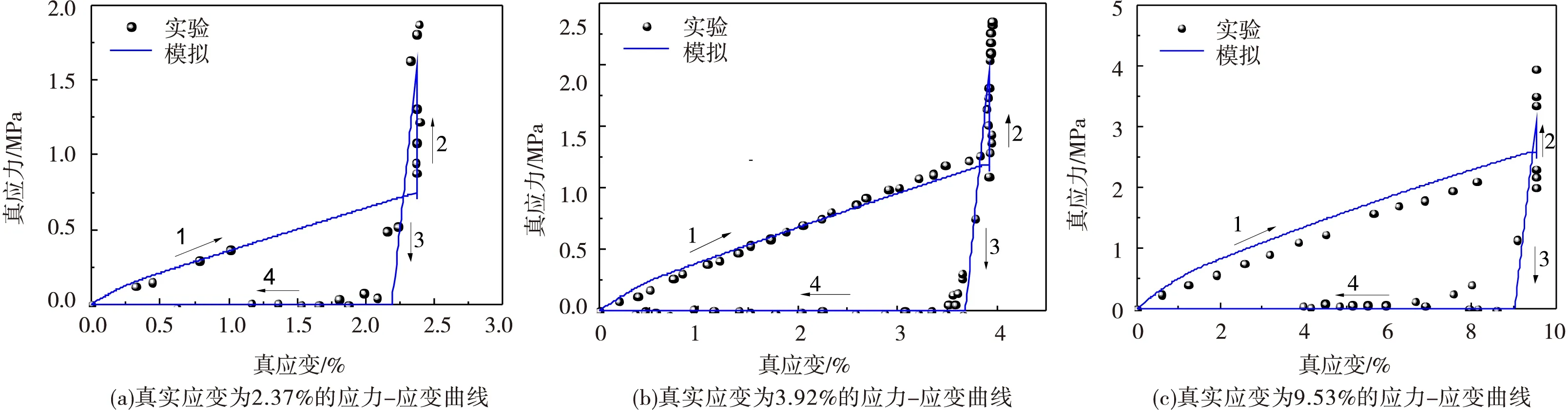
图1实验和模拟的应力-应变曲线

图2为不同应变下实验和模拟的应力-温度曲线，从图中可以得出：在高温加载阶段(第1阶段)，温度不发生变化，应力增加；在降温阶段(第2阶段)，应力随着温度的降低而增加，并且温度低于玻璃化转变温度Tg时应力迅速增加，这是由于温度低于玻璃化转变温度Tg时材料模量迅速增加。在位移卸载阶段(第3阶段)，应力降低为零；在升温阶段(第4阶段)，应力不发生变化。不同峰值真应变下的模拟结果和试验结果吻合很好。

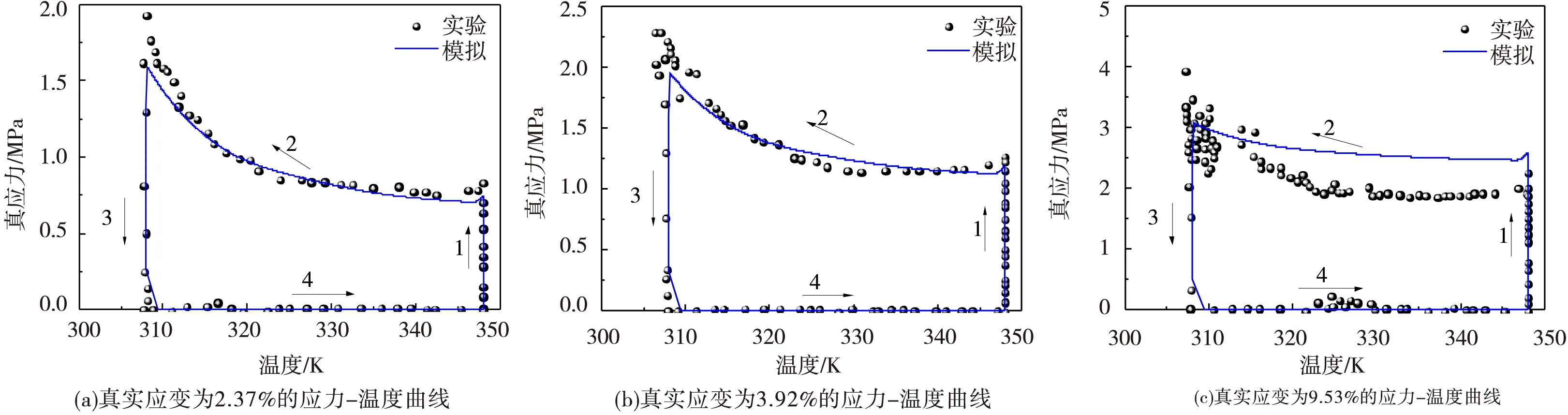
图2实验和模拟的应力-温度曲线

图3为不同应变下实验和模拟的应变-温度曲线，从图中可以得出：在高温加载阶段(第1阶段)，温度不发生变化，应变增加；在降温阶段(第2阶段)，保持应变不发生变化，温度降低；在卸载阶段(第3阶段)，由于卸载产生了一些恢复应变；在升温阶段(第4阶段)，在玻璃化转变温度Tg以下时，分子链处于冻结态，其形状恢复率较低，当温度达到Tg附近时，分子链被激活，形变恢复率增加。不同峰值真应变下的模拟结果和试验结果吻合较好。

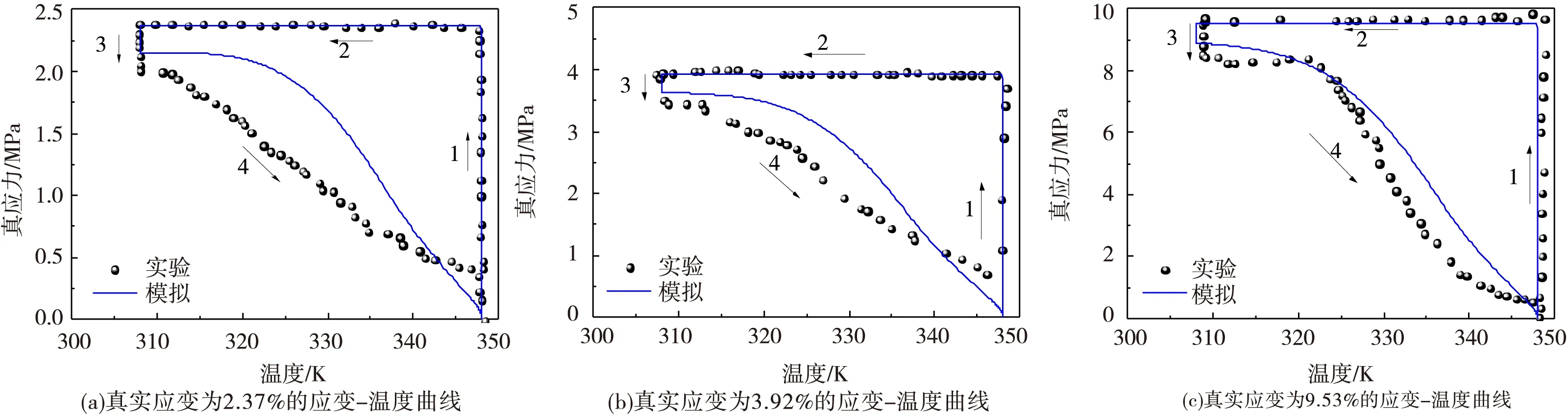
图3实验和模拟的应变-温度曲线

3　结束语

在粘弹性聚合物理论基础上给出新的时温等效方程来模拟形状记忆聚合物的形状记忆热力学过程。通过在峰值加载应变下的应力、应变和温度变化实验曲线与模拟曲线的对比可知，采用的粘弹性、超弹性和时温等效方程能较好地描述玻璃态热致形状记忆聚合物的形状记忆效应。

[1] RATNA D,KARGER-KOCSIS J.Recent advances in shape memory polymers and composite:A review[J].Journal of Materials Science,2008,43(1):254-269.

[2] LIU C,QIN H,MATHER P T.Review of progress in shape-memory polymers[J].Journal of Materials Chemistry,2007,17(17):1543-1558.

[3] TOBUSHI H,HASHIMOTO T,HAYASHI S,et al.Thermomechanical constitutive modeling in shape memory polymer of polyurethane series[J].Journal of Intelligent Material Systems & Structures,1997,8(8):711-718.

[4] TOBUSHI H,OKUMURA K,HAYASHI S,et al.Thermomechanical constitutive model of shape memory polymer[J].Nihon Kikai Gakkai Ronbunshu A Hen/transactions of the Japan Society of Mechanical Engineers Part A,2001,33(10):545-554.

[5] LIU Y,GALL K,DUNN M L,et al.Thermomechanics of shape memory polymers:uniaxial experiments and constitutive modeling[J].International Journal of Plasticity,2006,22(2):279-313.

[6] 李郑发,王正道,熊志远,等.形状记忆聚合物热力学本构方程[J].高分子学报,2009,22(1):23-27.

[7] 周博,刘彦菊,冷劲松.形状记忆聚合物的宏观力学本构模型[J].中国科学:物理学、力学、天文学,2010,40(7):896-903.

[8] BAGHANI M,ARGHAVANI J,NAGHDABADI R.A finite deformation constitutive model for shape memory polymers based on Hencky strain[J].Mechanics of Materials,2014,73(1):1-10.

[9] GUO X G,LIU L W,ZHOU B,et al.Constitutive model for shape memory polymer based on the viscoelasticity and phase transition theories[J].Journal of Intelligent Material System &Structures,2016,27(3):314-323.

[10] 王浩.橡胶材料的超弹性本构模型在轮胎分析中的应用[D].哈尔滨:哈尔滨工业大学,2008.

[11] 何平笙.高聚物的力学性能[M].合肥:中国科技大学出版社,2008.

A Model of Glassy Shape Memory Polymer Based on Time-temperature Equivalence Principle

ZHANGZebin1,2,KANQianhua1,2,DONGShiyu1,2,LIJian1,2,KANGGuozheng1,2

(1.Sichuan Key Laboratory of Applied Mechanics and Structure Security, Chengdu 610031, China;2.School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Based on viscoelastic theory of polymer and time-temperature equivalence principle, the shape memory process of the glassy shape memory polymer was simulated. The viscoelastic stress and strain of shape memory polymer can be divided into two parts: the stress depending on strain and the relaxation depending on time. The stress part uses the incompressible Mooney-Rivlin hyper-elastic model and the relaxation part is expressed by the Prony series. The temperature dependence of the modulus is implemented by a new time-temperature equivalence equation. Finally, it was found that the simulations were good agreement with the existed experiments.

shape memory polymer; viscoelasticity; hyper-elastic; time-temperature equivalence

2016-03-10

国家自然科学基金 (11572265)

张泽斌(1992-)，男，河南焦作人,硕士,主要从事形状记忆聚合物本构关系研究，(E-mail)zzblx@foxmail.com;

阚前华(1980-)，男，河南信阳人,副教授，博士,主要从事智能材料循环本构关系研究，(E-mail)qianhuakan@foxmail.com

1673-1549(2016)03-0066-04

10.11863/j.suse.2016.03.14

TB381

A