基于T型燃烧器的非线性不稳定参数分析①

金秉宁，刘佩进，魏祥庚，吕　翔，刘　鑫，魏少娟

(西北工业大学 燃烧、热结构与内流场重点实验室，西安　710072)



基于T型燃烧器的非线性不稳定参数分析①

金秉宁，刘佩进，魏祥庚，吕翔，刘鑫，魏少娟

(西北工业大学 燃烧、热结构与内流场重点实验室，西安710072)

基于脉冲触发T型燃烧器技术，对T型燃烧器内的平衡压强上升(DC Shift)和初始极限幅值进行测量，获得DC Shift、初始极限振幅以及压强耦合响应函数(Rp)三者之间的相互关系。实验结果表明，T型燃烧器中可测量得到推进剂燃烧产生的平衡压强上升现象，且与初始极限振荡幅值的二次方成正比；推进剂配方对DC Shift影响较大，即压强耦合响应函数值越高，推进剂燃烧产生DC Shift越大；推进剂压强耦合响应函数、初始极限幅值和DC Shift三者之间存在一定的耦合关系，这一结果与Flandro的平衡压强上升理论基本一致。

非线性不稳定; T型燃烧器技术; 平衡压强上升; 初始极限幅值；燃烧响应函数

0　引言

近年来，火箭发动机中的非线性燃烧不稳定问题较严重[1-3]。这种不稳定问题常常表现出较大的平衡压强上升(DC Shift)、有限振幅振荡(limit amplitude)以及高幅振荡中高阶振荡模态传递变化等现象。分析认为，这种非线性不稳定问题，往往都是由某种触发机制造成的[4-5]。因此，需要针对这种燃烧不稳定问题开展深入的研究。

理论方面，基于声扰动建立的标准稳定性预估程序(SPP)，是通过计算一系列增长系数来表征发动机不稳定的线性特性[6-7]。然而，对于发动机内压强振荡会达到什么样的幅值，或者是否能产生DC Shift的变化，线性稳定理论是无法给予满意的解释，这就需要非线性燃烧不稳定分析方法[8-11]。非线性燃烧不稳定性分析方法，对压强振荡所达到的极限幅值和平衡压强上升是可进行简单的预估[12-13]。但该分析方法中增益和阻尼因素考虑不够全面，其结果与真实发动机的压强曲线数据不能很好地对应，且模型中很大一部分参数需要通过实验测量获得。因此，实验测量工作是研究燃烧不稳定的重要部分。

实验方面，全尺寸发动机实验能反映出真实发动机不稳定问题，但其成本高，较难开展大量的实验测量；而针对某些主要影响因素的部件实验在解决燃烧不稳定问题中起到了非常重要的作用，被广泛采用。其中，基于脉冲触发T型燃烧器方法，用来测量火箭发动机中最主要的增益因素——推进剂燃烧响应，被广泛使用，且获得了一些有价值的实验结果。然而，其测量过程中使用外部脉冲触发造成的T型燃烧器内平衡压强上升和初始极限振荡幅值与真实发动机中DC Shift和limit amplitude存在一定差异，对于其测量结果是否能反映真实发动机中非线性不稳定趋势的研究报道相对较少。

本文基于脉冲触发T型燃烧器方法[14]，通过不同脉冲触发压强，对T型燃烧器内的平衡压强上升和初始极限幅值进行测量，并结合Flandro的非线性不稳定分析方法，讨论了二者之间的耦合关系，获得一些有价值的规律；而后，探讨了不同推进剂配方对平衡压强上升和初始极限幅值的影响作用。

1　实验方法及内容

1.1实验方法

图1为典型的T型燃烧器脉冲触发实验压强曲线。之所以采用脉冲激励方法，主要是因为高含铝量的复合推进剂在T型燃烧器内产生自激振荡较困难，需要一种外部扰动激励，使其在T型燃烧器内产生自激振荡现象。其工作原理是脉冲激励产生的高温高压燃气进入T型燃烧器内产生高振幅的瞬态扰动波动，与固有声场耦合产生周期性的声波振荡，并与推进剂燃烧表面产生耦合响应，进一步放大声波振荡幅值，从而在T型燃烧器内的形成自激声振荡。其自激声振荡频率为T型燃烧器的固有声频率，与其长度有关。

图1　典型脉冲实验压强时间曲线

其中，脉冲工作压强范围约为15～70 MPa，脉冲触发位置为T型燃烧器两端声压振幅最大处，触发时刻在T型燃烧器工作中间时刻，并确保在触发之前T型燃烧器内没有压强振荡和平衡压强的变化。脉冲触发之后，T型燃烧器内的压强快速升高，产生明显的平衡压强变化，并伴有压强振荡现象，即脉冲触发产生的瞬态扰动波。该波动在传播过程中与声场耦合形成周期性的振荡波，该周期性的振荡波频率为固有声频率。该耦合过程速度较快，往往发生在脉冲扰动波产生之后的较短时间内，并且直到与声场耦合之后，才形成周期性的振荡，在此之前振荡波均为非周期振荡，如图1所示。当平衡压强达到最大时，脉冲振荡波与声场以及推进剂燃烧表面响应的耦合作用已经完成，周期性的压强振荡幅值达到最大，即初始极限幅值。之后，由于系统内阻尼作用大于增益作用，压强振荡呈衰减趋势。其中，平衡压强变化、脉冲触发压强和初始极限振幅如图1中所定义。

1.2实验内容

为获得由T型燃烧器内推进剂燃烧产生的平衡压强上升(即DC Shift)和相应的初始极限幅值等参数影响，排除脉冲触发自身在激励中造成的平衡压强增大和振荡幅值变化。因此，需要分别开展无推进剂燃烧和有推进剂燃烧条件下的实验测量工作。其中，无推进剂燃烧实验部分采用高压氮气模拟给定的平衡压强，在密闭T型燃烧器环境下进行脉冲触发实验。有推进剂燃烧实验工作压强和脉冲参数均与无推进剂燃烧实验相同。两部分实验结果见表1。

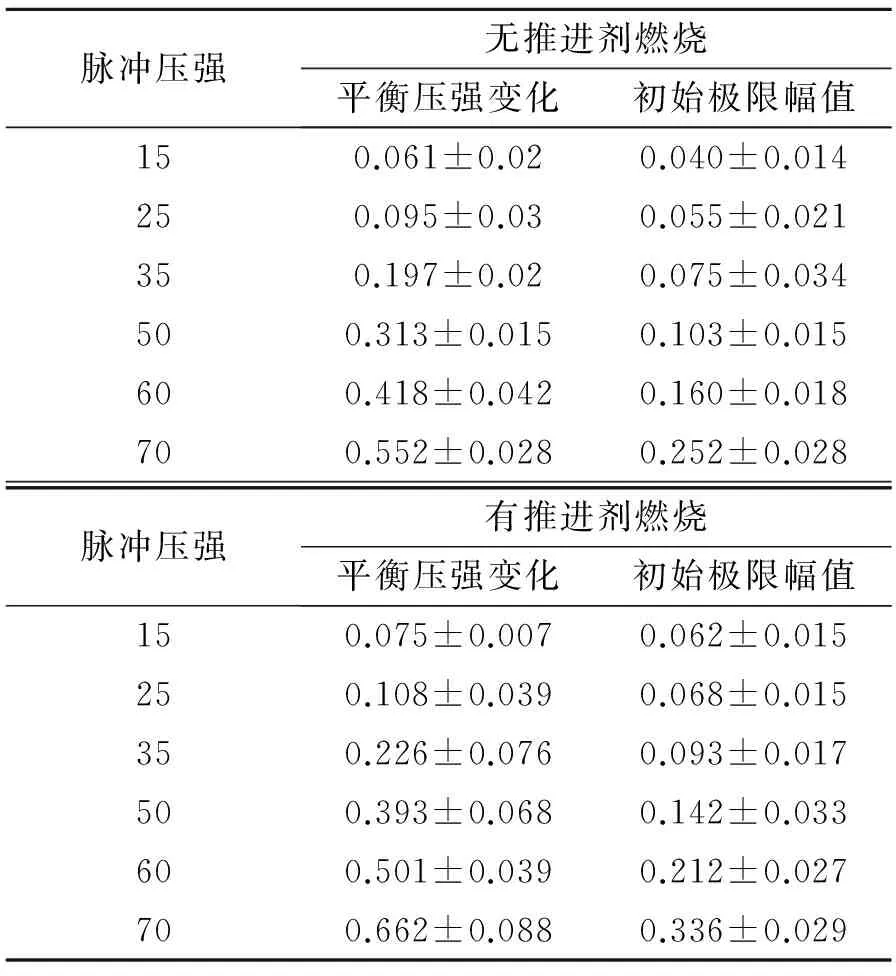
表1　有无推进剂燃烧条件下的脉冲触发实验测量结果

从表1可看出，随着脉冲触发压强从15～70 MPa的逐渐增大，无推进剂燃烧条件下，T型燃烧器内的平衡压强和初始振荡幅值均呈明显增大趋势，变化范围分别为0.061～0.552 MPa和0.04～0.252 MPa。分析认为，在密闭条件下，外部脉冲触发的工质注入到T型燃烧器内，使得T型燃烧器内总质量增大，原本的平衡状态发生变化，表现出平衡压强增大。这种平衡压强增大，与推进剂燃烧无关，是由脉冲触发自身在激励中造成的。因此，这里的平衡压强变化只能认为是平衡压强增大，不能称之为DC Shift。同时，由于T型燃烧器是一个封闭的声腔，其工质中的部分热能向声场传递，使得声振能量加大，相应振荡幅值增大。但该部分振荡幅值较小，与推进剂燃烧无关。

同样，有推进剂燃烧条件下，随着脉冲触发压强的增大，平衡压强和初始振荡幅值均呈明显的增大趋势，变化范围0.075～0.662 MPa和0.062～ 0.336 MPa。分析认为，脉冲触发一方面增加了系统内的质量流率(脉冲器内的质量流率注入T型燃烧器内)，使得总质量生成率大于喷管出口质量流率，系统内原本平衡的状态发生变化，造成平衡压强增大；另一方面，平衡压强增大，使得推进剂燃烧特性发生改变，与推进剂燃烧产生耦合作用，瞬态燃速增大，造成总质量生成相应增大，平衡压强进一步上升。同样，在声振荡幅值最大位置处(即在T型燃烧器两端位置)注入的能量越大，向声场传递的能量也越大，使得声振能量加大，相应振荡幅值增大；同时，增大的振荡幅值又与推进剂燃面发生耦合作用，使得推进剂在燃烧过程中产生周期性的质量流率和释放热，进一步增大声振荡幅值。下面将对这两种条件下的实验结果进行对比分析。

2　实验结果分析

2.1DC Shift和初始极限幅值结果分析

图2为有推进剂燃烧和无推进剂燃烧条件下的脉冲压强对平衡压强影响关系。从图2可看出，有推进剂燃烧条件下脉冲触发产生的平衡压强上升值要略高于无推进剂燃烧条件下脉冲触发产生的平衡压强上升。随着脉冲触发压强的增大，二者差值逐渐增大，差值约为0.013～0.111 MPa，相对于无推进剂燃烧条件下的DC Shift值来说，前者相对增大幅度约为13.8%～25.3%。

分析认为，这种压强上升的差值就是由推进剂燃烧造成的。脉冲触发对推进剂的燃烧过程有较大的影响，使得平衡压强升高与推进剂燃烧发生耦合作用，增大推进剂燃烧速率，从而进一步增大推进剂质量流率，打破原有的平衡状态，增大T型燃烧器内的平衡压强，产生平衡压强上升(DC Shift)。

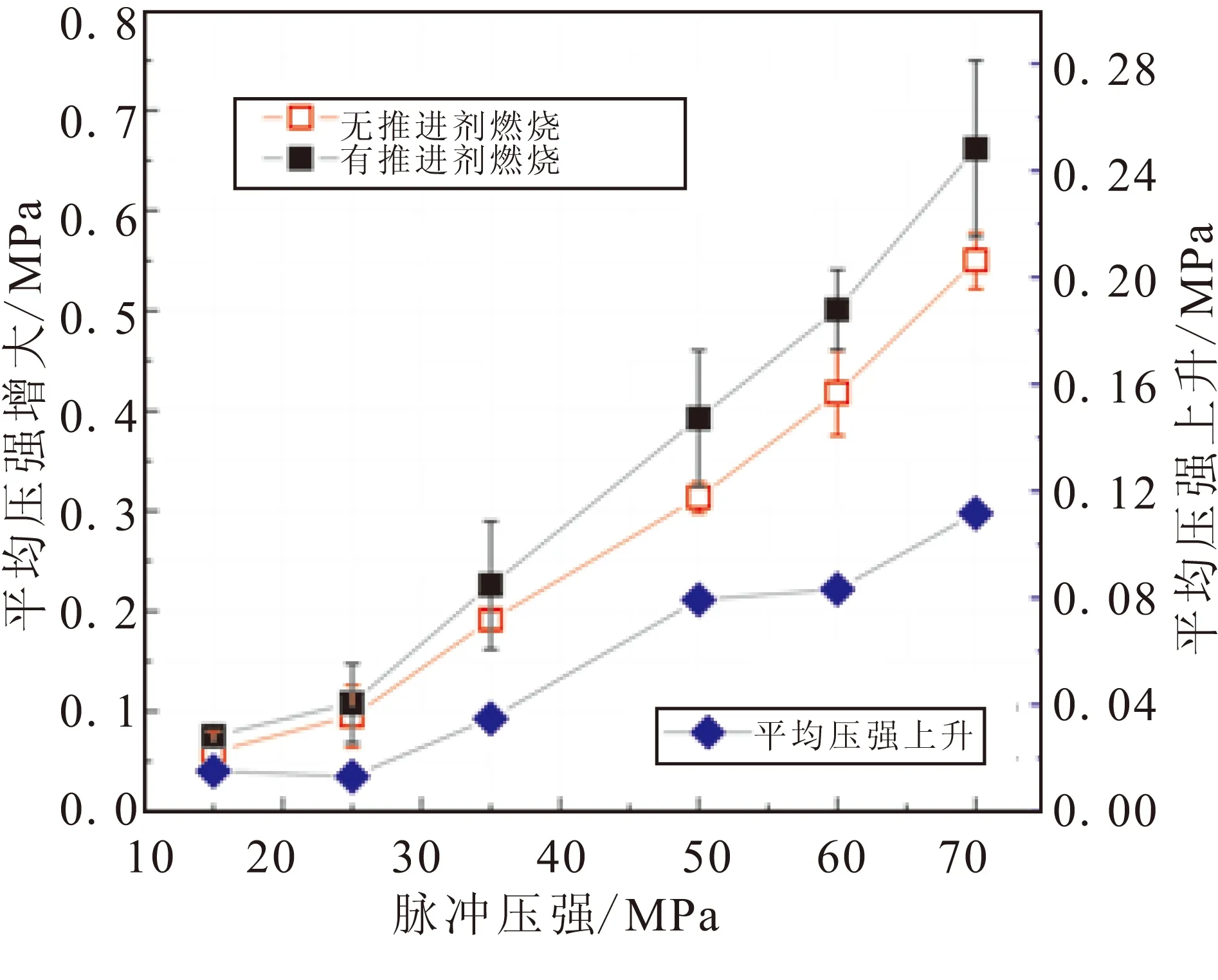
图2　脉冲触发压强与DC Shift关系

图3为脉冲触发压强对初始极限幅值的影响关系。随着脉冲触发压强的增大，有推进剂燃烧和无推进剂燃烧条件下的初始极限振荡幅值均呈增大的趋势，且有推进剂燃烧条件下的初始极限幅值增大趋势要明显高于无推进剂条件下，在高脉冲触发压强条件下，增大趋势尤为明显。二者之间的差值约为0.013～0.087 MPa，增大的幅度约为24.5%～55.5%。

分析认为，推进剂燃烧对振荡幅值影响较大。推进剂在燃烧过程中受初期的小幅声振荡的影响，产生周期性的能量释放，并向声场传递，与声场发生耦合作用，进一步增大推进剂燃烧释放能量，从而进一步增大声振荡作用。

图3　脉冲压强对初始极限幅值影响

图2和图3结果表明，在T型燃烧器内，通过脉冲触发激励方式，可观测到由推进剂燃烧产生的平衡压强上升现象(即DC Shift)和初始极限幅值变化。下面将结合Flandro的非线性不稳定分析方法，讨论DC Shift 和初始极限幅值二者之间的相互关系。

2.2DC Shift与初始极限振幅关系

Flandro的能量平衡方法[2]认为，平衡压强上升(DC Shift)与声波系统的增长和极限振幅关系密切，平衡压强和声压振荡幅值均是时间的缓变函数，如式(1)所示：

(1)

式(1)中，平衡压强的变化率是压强振荡幅值的非线性函数，第一项由标准稳态内弹道计算方法获得，与推进剂表面质量生成率和喷管质量流出率有关；第二项与振荡幅值、燃面马赫数和响应函数有关，且平衡压强变化率与压强振荡极限振荡幅值的平方ε2和压强耦合响应函数(Rp)成正比。这说明当平衡压强上升所需时间一定时，平衡压强上升值大小与振荡极限幅值和推进剂压强耦合响应函数之间是强耦合关系。

图4为T型燃烧器内脉冲触发实验测量得到的平衡压强上升与压强振荡极限幅值二者之间的关系图。从图4很明显看出，平衡压强上升与初始极限幅值近似呈二阶增长，即平衡压强上升与压强振荡极限振荡幅值二次方成正比，也即随着平衡压强上升，燃烧室内能量向声场传递，使得声场能量逐渐增大，振荡幅值也是一个逐渐增长的过程。

图4中的实验结果与方程(1)趋势基本一致，这表明T型燃烧器中测量到的平衡压强上升和初始极限幅值二者之间的耦合关系与Flandro的能量平衡方法中的结果趋势相一致。

2.3响应函数对DC Shift和AMP影响

实际发动机中，影响DC Shift 和极限振荡幅值的因素更为复杂，除了与非稳态动力学和模态之间的能量传递有关，还与推进剂燃烧特性有很大关系。通过前期的研究发现[15]，不同推进剂配方对推进剂的响应函数有较大影响。因此，针对2种不同响应函数值的推进剂进行了脉冲触发实验，获得了在推进剂燃烧条件下的DC Shift和初始极限振荡幅值。其中，推进剂样品A在f=～255 Hz条件下的响应函数值约为0.47，在f=～140 Hz条件下响应函数值约为0.8，推进剂样品B在f=～255 Hz条件下的响应函数值约为1.56。推进剂燃烧平衡工作压强约为7 MPa，脉冲激励压强约为25 MPa。典型的实验结果如表2所示。

图4　平衡压强上升与初始极限幅值关系

表2　2种不同响应函数值推进剂实验结果对比

注：1)、2)值为无推进剂燃烧条件下相对应的平衡压强上升和振幅值。

2.3.1响应函数的影响

从表2可看出，在振荡频率约为255 Hz条件下，响应函数值较低的推进剂产生的平衡压强上升值小于响应函数值较高的推进剂。这说明，在相同振荡频率条件下，推进剂燃烧响应特性对DC Shift有较大影响，即推进剂燃烧响应特性对不稳定燃烧是一种增益作用，在T型燃烧器工作过程中，增大了振荡幅值，同时改变了推进剂的燃烧性能，从而进一步增大平衡压强。因此，推进剂燃烧响应的不同，即推进剂配方的变化，在T型燃烧器中燃烧产生的DC Shift有明显的不同。

2.3.2振荡频率的影响

同时，推进剂压强耦合响应函数又是振荡频率的函数，相同推进剂在不同振荡频率条件下的响应函数值有明显的不同，如表2中所示。在相同工作压强条件下，推进剂A在140 Hz条件下的响应函数平均值值约为 0.8，高于255 Hz条件下平均值0.47，相对应产生的DC Shift和振荡幅值约为明显高于在255Hz振荡频率条件下的DC Shift和振荡幅值，即不同振荡频率条件下，推进剂燃烧产生的非线性特性有明显不同。

分析认为，振荡频率的变化改变推进剂燃烧响应特性，从而对振荡幅值和DC Shift产生影响。推进剂响应函数、初始极限幅值和DC Shift三者之间存在一定的耦合关系，即当推进剂配方变化时，其相应的压强耦合响应函数发生改变，在相同的触发激励作用下，产生的DC Shift有明显不同，同时初始极限幅值平方与DC Shift成正比，从而使振荡幅值发生变化，变化的振荡幅值与推进剂燃烧进一步产生耦合，从而改变推进剂燃烧响应特性。

综上所述，利用T型燃烧器测量技术，可观测到平衡压强上升现象，且平衡压强上升与初始极限幅值是二次方的关系；同时，推进剂配方参数对平衡压强上升有一定影响。这一结果与Flandro的平衡压强上升理论基本相一致。这表明T型燃烧器实验测量结果有助于研究真实发动机中的DC Shift等问题，将T型燃烧器实验测量结果与真实发动机结果联系起来进行分析，将是今后的研究重点，需要进一步开展更多的研究工作。

3　结论

(1)利用T型燃烧器技术，可测量得到推进剂燃烧产生的平衡压强上升现象，且平均压强上升与初始极限振荡幅值的二次方成正比。

(2)不同配方推进剂燃烧对DC Shift影响较大，即压强耦合响应函数越高的推进剂燃烧产生的DC Shift越大。

(3)DC Shift与推进剂响应函数和初始极限幅值三者之间存在一定的耦合关系，这一结果与Flandro的平衡压强上升理论基本一致。

[1]Blomshield F S,Mathes H B,Crump J E,et al.Nonlinear stability testing of full-scale tactical motors[J].Journal of Propulsion and Power,1997,13(3):356-366.

[2]Flandro G A,Fischbach S R,Majdalani J,et al.Nonlinear rocket motor stability prediction:limit amplitude,triggering and mean pressure shift[R].AIAA 2004-4054.

[3]Malhotra S,Flandro G A.On nonlinear combustion instability [J].AIAA 97-3250.

[4]刘佩进,金秉宁,李强.战术导弹固体发动机燃烧不稳定研究概述[J].固体火箭技术,2012,35(4):446-449+456.

[5]胡大宁,何国强,刘佩进,等.翼柱型药柱固体火箭发动机不稳定燃烧研究[J].固体火箭技术,2010,33(5):502-506.

[6]Culick F E C.Acoustic oscillations in solid propellant rocket chambers[J].Acta Astronautica,1966,12(2):113-126.

[7]Culick F E C.Unsteady motions in combustion chambers for propulsion systems[M].Virginia:National Technical Information Service Springfield,2006.

[8]Culick F E C.Nonlinear behavior of acoustic waves in combustion chambers[R].Jet Propulsion Laboratory,NASA,April 1975,NASA-CR-149376.

[9]Flandro G A.Energy balance analysis of nonlinear combustion instability[J].Journal of Propulsion and Power,1985,1(3):210-221.

[10]Flandro G A.Approximate analysis of nonlinear instability with shock waves[R].AIAA 82-1220.

[11]Baum J D,Levinet J N,Lovine R L.Pulsed instability in rocket motors:a comparison between predictions and experiments[J].Journal of Propulsion and Power,1988,4(4):308-316.

[12]French J C,Flandro G A,Majdalani J.Improvements to the linear standard stability prediction program(SSP)[R].AIAA 2004-4181.

[13]Flandro G A,Majdalani J,French J C.Incorporation of nonlinear capabilities in the standard stability prediction program[R].AIAA 2004-4182.

[14]刘佩进,齐宗满,金秉宁,等.两种含铝复合推进剂压强耦合响应的试验对比[J].固体火箭技术,2013,36(1):83-88.

(编辑：吕耀辉)

Parameter analysis of nonlinear combustion instability based on T-burner

JIN Bing-ning,LIU Pei-jin,WEI Xiang-geng,LV Xiang,LIU Xin,WEI Shao-juan

(Science and Technology on Combustion,Internal Flow and Thermal-Structure Laboratory,Northwestern Polytechnical Univ., Xi'an710072,China)

Based on the pulsing trigger T-burner technique,some results were obtained on the relationship between the DC Shift,the initial limit amplitude and the pressure coupled response function.The result shows that,the propellant combustion has a great influence on the DC Shift and the initial limit amplitude.Also,the propellant with different formulations has a great influence on the DC Shift,which means that the higher the pressure response functions,the bigger DC Shift produced by the propellant burning would be.For nonlinear instability,there is a certain coupling relationship between the pressure response function of the propellant, the initial limit amplitude and the DC Shift,and the results are consistent with the theory of Flandro.

nonlinear instability;T-burner;DC Shift;initial limit amplitude,combustion response function

2015-11-01；

2016-01-22。

国家自然科学基金(51206136)；中央高校基本科研业务(3102014ZD0032)。

金秉宁(1986—)，男，博士生，研究领域固体火箭发动机燃烧不稳定及控制技术。E-mail：xuelang-8655@163.com

V435

A

1006-2793(2016)03-0301-05

10.7673/j.issn.1006-2793.2016.03.001