基于二级剪枝策略的正负关联模式挖掘算法
2016-11-02苏雪峰郭燕萍
苏雪峰,郭燕萍,胡 彧
(1.山西大学商务学院,山西太原030031;2.太原理工大学,山西太原030024)
基于二级剪枝策略的正负关联模式挖掘算法
苏雪峰1,郭燕萍1,胡 彧2
(1.山西大学商务学院,山西太原030031;2.太原理工大学,山西太原030024)
为了解决负关联规则挖掘中海量项集问题和一级剪枝策略效率不高的问题,首先给出一种计算项集和关联规则兴趣度的数学模型,然后提出基于兴趣度的项集剪枝和关联规则剪枝的二级剪枝策略,最后提出一种新的基于二级剪枝策略的正负关联模式挖掘算法B-PANR。该算法采用新的剪枝技术,避免无效的或者无趣的正负模式产生,正负关联规则数量和挖掘时间明显降低,挖掘效率得到很大提高。理论分析和实验结果表明,与现有代表性挖掘算法PARamp;NAR和IPARamp;NAR比较,B-PANR算法在挖掘效率、剪枝效果和稳定性方面具有很好的表现,并且具有良好的扩展性。
兴趣度;剪枝;正负关联规则;B-PANR算法
关联规则挖掘是数据挖掘中重要研究分支和研究热点之一,旨在从大量数据中发现和分析项集之间有趣的各种关联,以揭示隐藏其中的事务内在本质联系。其早期的研究是以正关联规则挖掘为主,典型的关联规则算法是Agrawal等人于1993年提出的Apriori算法。在Apriori算法的基础上,出现了很多改进算法[1]。典型的正负关联规则挖掘算法是Wu等提出的正负关联规则挖掘算法[2],在此基础上,产生了很多改进的正负关联规则挖掘算法,如基于多支持度的正负关联规则挖掘算法以及基于频繁模式树的正负关联规则挖掘算法[3]等。
与挖掘正关联规则相比,从数据库中挖掘负关联规则面临的挑战是候选项集数量巨大,如何有效地生成候选项集并进行合理的剪枝是当前关联规则挖掘的两大基本问题。针对这些问题,文献[2]提出了基于Apriori框架同时生成频繁项集和非频繁项集的方法,并利用兴趣度在候选项集生成和关联规则生成两个阶段进行剪枝。然而,当前的正关联规则剪枝技术研究比较充分,而对挖掘正负关联规则的项集剪枝和正负规则剪枝研究不是很深入。为此,本文从候选项集生成和剪枝两个层面展开研究。
1 相关知识
1.1 正负关联规则的定义
定义1已知A⊂I,B⊂I且A⋂B=∅,C1∈{A,¬A},C2∈{B,¬B},ms为最小支持度阈值,mc为最小置信度阈值,关联规则C1=>C2若满足:(1)supp(A)≥ms且 supp(B)≥ms;(2)supp(C1=>C2)≥ms;(3)conf(C1=>C2)≥mc,则称C1=>C2为有意义的正负关联规则[4]。
1.2 支持度与置信度的计算
设A,B为事务数据库D中的项集,其中A⋂B=,supp(A)为A的支持度,则正负关联规则支持度与置信度的计算公式如式(1)至式(7)所示[4]:


1.3 相关性计算
由于关联规则A=>B的置信度只是在给定A条件下B的概率估计,它并不能反映A与B之间相关的强度,而关联规则蕴涵的应该是正相关关系,负相关关系的关联规则是没有实际意义的。目前普遍采用的计算项集相关性的方法是Brin[4]提出的公式:

其中corrA,B∈[0,+∞),当corrA,B<1时,项集A和B为负相关,表示A与B呈抑制作用;当corrA,B=1时,项集A和B相互独立;当corrA,B>1时,项集A和B为正相关,表示A与B互相促进。
文献[4]证明了项集A与B之间相关性具有如下关系:
(1)当corrA,B>1 时 ,corr¬A,B<1 ,corrA,¬B<1 ,corr¬A¬,B> 1 ;
(2)当corrA,B=1 时 ,corr¬A,B=1 ,corrA,¬B=1 ,corr¬A¬,B=1 。
2 基于兴趣度模型的二级剪枝策略
在corrA,B的基础上提出了兴趣度模型,用来更精确地反映关联规则相关的程度,同时克服了corrA,B在临界值1的两侧值的分布不对称的不足。
2.1 关联规则的兴趣度
conf(A=>B)<conf(¬A=>B)表明购买A的情况下购买B的概率比不购买A的情况下购买B的概率要低,购买A对购买B起抑制作用,A与B之间是负相关关系,¬A,B为正相关关系。所以很自然地可建立如下兴趣度模型[5]:
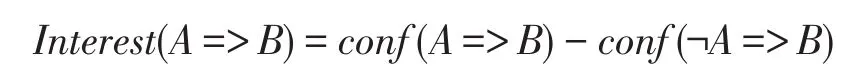
根据正负关联规则支持度与置信度计算的相关公式,对上述公式进行推导,过程如下:
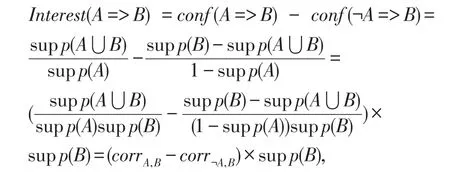
由上述等式可得出如下规范化兴趣度模型:

其中max{corrA,B-corr¬A,B}为规范化因子,使得兴趣度的值域为[-1,1]。容易证明当corrA,B>1时;Interest(A=>B)>0,corrA,B<1时,Interest(A=>B)<0;corrA,B=1时,Interest(A=>B)=0;|Interest(A=>B)|的值越大,相关性越强。
定义2已知A⊂I,B⊂I且A⋂B=∅,C1∈{A,¬A},C2∈{B,¬B},ms为最小支持度阈值,mc为最小置信度阈值,mi为最小兴趣度阈值,C1=>C2是有意义的关联规则,且|Interest(C1=>C2)|≥mi,则称C1=>C2为有趣的关联规则。
2.2 项集的兴趣度
当项集{AB}的相关性corrA,B>1时,关联规则A=>Bt¬A=>¬B的前件和后件是正相关关系,若两个规则的兴趣度都小于mi,则项集{AB}应该剪枝;若两个规则中有一个规则的兴趣度小于mi,项集{AB}保留,不满足mi要求的规则在关联规则生成阶段剪枝;故可选择两个规则最大的兴趣度作为项集{AB}的兴趣度,项集{AB}的兴趣度记为:
InterestA,B=max{Interest(A=>B),Interest(¬A=>¬B)},
同理,当项集{AB}项集的相关性corrA,B<1时,只生成关联规则A=>¬B和¬A=>B,故

当项集{AB}项集的相关性corrA,B=0时,不生成任何形式的关联规则,项集{AB}应该剪枝。将三种情况综合可得项集{AB}的兴趣度模型为:

InterestA,B的值域为[-1,1],其值在0的两侧对称,且当InterestA,B<0时,项集A与B负相关,InterestA,B>0时,项集A与B正相关,InterestA,B=0时,项集A与B相互独立。
2.3 二级剪枝策略
在正负关联规则挖掘过程中,目前的研究主要在关联规则生成阶段进行剪枝。众多研究表明,频繁项集中只有一小部分项集能生成有趣的关联规则,所以在频繁项集生成过程中实施剪枝也非常重要。
2.3.1 项集剪枝
由项集兴趣度的定义可知,当项集兴趣度小于最小兴趣度阈值mi,这些项集不可能生成有趣的关联规则,项集剪枝就是要对这类项集实施剪枝。若项集X不满足条件(10)约束,则需要将其剪枝,否则保留。

2.3.2 关联规则剪枝
已知频繁项集X={AB},当InterestA,B<0,则生成关联规则A=>¬B,¬A=>B;当InterestA,B>0,则生成关联规则A=>B,¬A=>¬B。关联规则A=>B是有趣关联规则需要满足最小支持度阈值ms,最小置信度阈值mc和最小兴趣度阈值mi。故A=>B是有趣关联规则需要满足条件(11)的约束,否则实施剪枝。
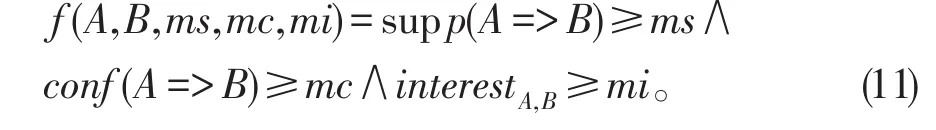
同理,关联规则A=>¬B,¬A=>B,¬A=>¬B是否有趣也可按上述方法进行验证。
二级剪枝策略可以采取一致的最小兴趣度阈值mi,即项集和关联规则兴趣度阈值相等;也可以采取不一致的最小兴趣度阈值,即分别设置项集和关联规则兴趣度阈值为mi和mri,且mi<mri。一致阈值实现简单易于理解,二级阈值更加灵活,扩展性强。
3 算法设计
本文设计的正负关联规则挖掘算法B-PANR(Both Positive and Negative Association)分成搜索有趣频繁项集和生成正负关联规则两个子过程,并在两个子过程中分别使用项集兴趣度和关联规则兴趣度实施剪枝。
算法1:有趣项集生成算法Search-ItemsetsOfInterest
输入:事务数据库D;最小支持度阈值ms;最小兴趣度阈值mi;
输出:有趣项集的集合IL;
过程:
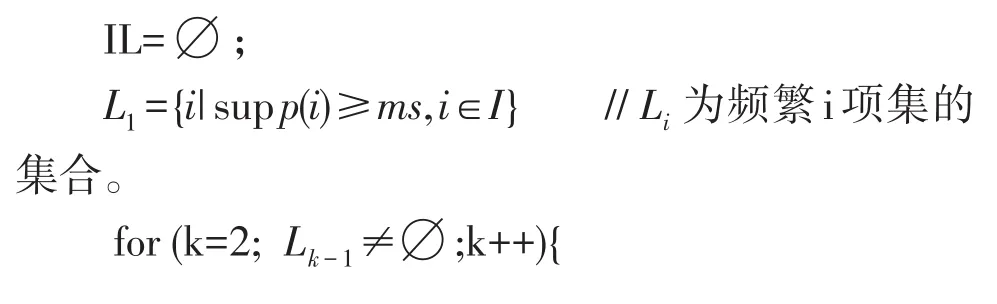

算法2:基于兴趣度的正负关联规则生成算法PositiveAndNegtativeRules
输入:有趣项集的集合IL;最小支持度阈值ms;最小置信度阈值mc;最小兴趣度阈值mi;
输出:正负关联规则集合AR;过程:

4 实验与分析
4.1 实验设计
为了验证本文提出的基于兴趣度挖掘正负关联规则的算法B-PANR的效率与剪枝效果,实验选取了3个数据集、2种类似算法进行了对比实验。实验数据采用频繁项集和关联规则挖掘普遍使用的合成数据,数据来源为 SPMF 网站 http:∕www.philippe-fournier-viger.com∕spmf∕和频繁项集挖掘数据集 http:∕fimi.ua.ac.be∕data∕。数据集的特征如表 1所示,其中T表示每一个事务中平均包含的项目数,I表示最大的频繁项集包含的平均项目数,D表示数据集包含的事务数。2个类似算法为董祥军等在文献[9]中提出的PARamp;NAR算法与吕杰林等在文献[10]提出基于兴趣度的IPARamp;NAR算法,PARamp;NAR算法没有使用兴趣度进行剪枝,直接由频繁项集生成正负关联规则,IPARamp;NAR算法在关联规则生成阶段使用兴趣度实施剪枝。算法实现是基于SPMF(序列模式挖掘框架)提供的JAVA开源数据挖掘程序类库v0.96(2014.4.6最新发布)。算法运行计算机配置为:主频2.5GHz,内存2GB的个人计算机。

表1 合成数据的基本特征
4.2 实验结果
4.2.1 支持度阈值变化时挖掘性能比较
为了验证B-PANR算法在不同支持度下的性能,实验选取T25I10D10k为实验数据集,设置mc=0.2,mi=0.1,对比三种算法在最小支持度阈值取不同值的情况下三种算法的运行时间和正负关联规则数量。实验表明,本文提出的B-PANR算法在不同支持度下运行时间最短,三者的运行时间对比如图1所示。三种算法在不同支持度下产生的正负关联规则数量如表2所示,其中B-PANR算法生成的规则数量最少。

图1 三种算法在不同支持度下的运行时间比较

表2 三种算法在不同支持度下生成的正负关联规则数量
4.2.2 兴趣度阈值变化时挖掘性能比较
为了验证B-PANR算法在不同兴趣度下的性能和剪枝效果,本文设计了B-PANR与IPARamp;NAR算法的比较实验,实验选取T25I10D10k为实验数据集,设置mc=0.2,ms=0.012。实验结果表明,随着兴趣度阈值不断增大,B-PANR算法的运行时间减少明显,而IPARamp;NAR算法的运行时间无明显变化,二者的运行时间如图2所示;B-PANR算法采用两阶段剪枝策略,随着兴趣度阈值不断增大,剪枝效果更明显,产生的规则数量远远小于IPARamp;NAR算法,实验结果如表3所示。

图2B-PANR与IPARamp;NAR算法在不同兴趣度下的运行时间比较

表3 B-PANR与IPARamp;NAR算法在不同兴趣度下的规则数量
4.2.3 不同数据环境下的挖掘性能比较
为了验证B-PANR算法在不同数据环境下的表现,实验选取表3中的三个数据集,在ms=0.012,mc=0.2,mi=0.1时,三种算法的运行时间比较如图3所示。

图3 三种算法在不同数据环境下的运行时间比较
实验结果表明B-PANR算法具有很好的可扩展性,又能很好地适应不同规模的数量集,尤其当数据集T和I较大时,B-PANR算法效果更加明显。在数据集T10I4D100K环境下,三种算法运行时间没有明显差异;在数据集T25I10D10k环境下,B-PANR运行时间略少于其它两种算法;在数据集T20I6D100k环境下,B-PANR运行时间明显少于其它两种算法。
4.3 实验结果分析
通过上述三个方面的实验表明,与IPARamp;NAR和PARamp;NAR算法相比,无论在不同支持度阈值、或者不同的兴趣度阈值和不同的数据集环境下,BPANR算法在运行时间和剪枝效果两个方面都具有一定的优势。
B-PANR算法优于其它两种算法的主要原因分析如下:
由于B-PANR算法采用两级剪枝策略,第一级剪枝通过项集剪枝减少了项集的规模,第二级剪枝通过关联规则剪枝减少了关联规则生成的数量,两个阶段都节约了运行时间。所以三种算法中,总体运行时间相对最少。
由于B-PANR算法在项集生成阶段对一些兴趣度较低的项集实施剪枝,减小了频繁项集的规模,所以生成的正负关联规则数量都要少于IPARamp;NAR算法。随着兴趣度阈值的不断提高,B-PANR算法的剪枝效果更明显。同时,本文提出的兴趣度规范了兴趣度的取值范围为[-1,1],克服了corrA,B∈[0,+∞)度量兴趣度时兴趣度阈值难确定的问题,使得基于兴趣度的剪枝效果更稳定。
5 结语
同时挖掘正负关联规则面临的巨大挑战是海量项集问题,为了提高算法的效率,剪枝是普遍采用的策略。而目前的研究主要在关联规则生成阶段实施剪枝,本文在研究兴趣度的基础之上提出了基于兴趣度模型的二级剪枝策略,并设计了BPANR算法,该算法在运行时间和剪枝效果上都优于未实施剪枝的PARamp;NAR与只实施关联规则剪枝的IPARamp;NAR算法,同时具有良好的稳定性和可扩展性。
[1]宋威,李晋宏.徐章艳,等.一种新的频繁项集精简表示方法及其挖掘算法的研究[J].计算机研究与发展,2010,47(2):277-285.
[2]WU X D,ZHANG C Q,ZHANG S C.Efficient Ming of Both Positive and Negative Association Rules[J].ACM Transactions on Information System,2004,33(3):318-405.
[3]RUCHI BHARGAVA,SHRIKANT LADE.Effective Positive Negative Association Rule Mining Using Improved Frequent Pattern Tree[J].International Journal of Advanced Research in Computer Science and Software Engineering,2013,3(4):193-199.
[4]董祥军,王淑静,宋瀚涛,等.负关联规则的研究[J].计算机工程,2004,24(11):978-981.
[5]吕杰林,陈是维.基于相关性度量的关联规则挖掘[J].浙江大学学报,2012,39(3):284-292.
Abdtract:In order to solve the question of large itemsets and improve the efficiency of one level pruning in mining negative association rules,the paper proposes a interestingness model to measure the itemset and association rule based on the research of relevance and interestingness of association rules,and designs two stage pruning strategy and B-PANR algorithm which is designed for achieving the two stage pruning strategy.Comparing with PARamp;NAR and IPARamp;NAR algorithm,B-PANR is proved more effective in executing time and pruning by experiments.
Research of Mining Positive and Negative Association Rules Based on Two-level Pruning Strategy
SU Xue-feng1,GUO Yan-ping1,HU Yu2
(1.School of Business,Shanxi University,Taiyuan Shanxi,030031;2.Taiyuan University of Technology,Taiyuan Shanxi,030024)
interestingness;pruning;positive and negative association rules;B-PANR algorithm
TP311
A
1674-0874(2016)01-0016-05
2015-10-20
山西省自然科学基金项目[2012011013-5];山西省软科学研究项目[2014041061-1];山西大学商务学院科研项目[2014011]
苏雪峰(1983-),男,山西偏关人,硕士,研究方向:数据挖掘与电子商务。
〔责任编辑 高海〕
