利用特征线法求解一维非齐次波动方程
2016-11-02樊龙
樊 龙
(山西大同大学煤炭工程学院,山西大同037000)
利用特征线法求解一维非齐次波动方程
樊 龙
(山西大同大学煤炭工程学院,山西大同037000)
对于非齐次波动方程的求解问题,一般情况下,我们通过齐次化原理(Duhamel原理)来给出方程解的具体形式。在文中,首先将方程化为方程组形式,然后应用特征线法给出该方程解的另一种推导过程。
非齐次波动方程;特征线;通解
首先,给出非齐次方程的初值问题
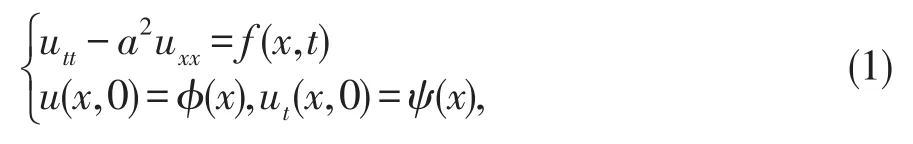
通过应用和文献[1]中同样的方法,可以将方程化简为以下形式
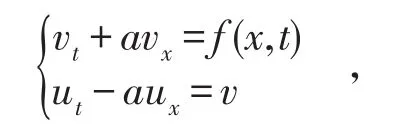

对于以上问题可以化为两部分
设方程(I)、(II)的解分别为u(1)、u(2),则u=u(1)+u(2)是原方程的解,下面分别求解。
对于方程(I)的解
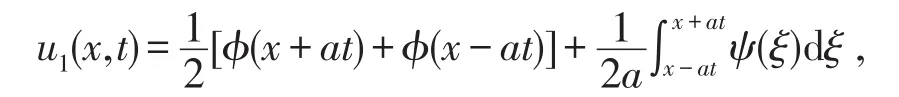
具体求解过程见文献[1]。
下面分析方程(II)解的具体算法。
方程(II)中(1)式,特征线为x1(t)=at+C1,沿特征线方向有

两边关于t在[0,t]上积分,
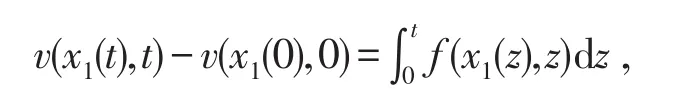
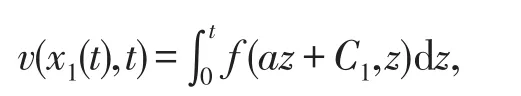
因v(x,0)=ut(x,0)-aux(x,0)=0,所以
由于C1=x1(t)-at,代入上式可得
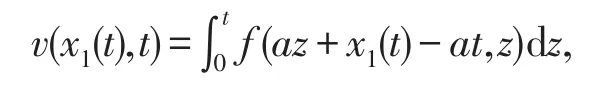
故方程(II)中(1)式的解为
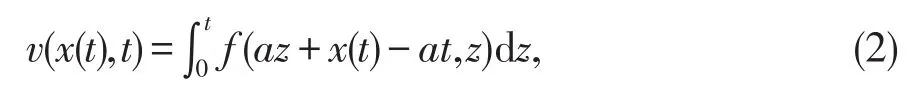
继续分析方程(II)中(2)式,特征线为
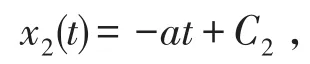
沿着特征线有
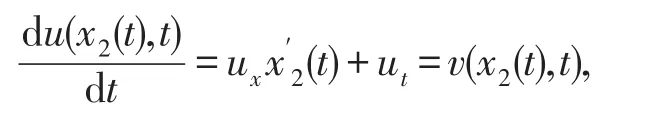
两边关于t在[0,t]上积分,
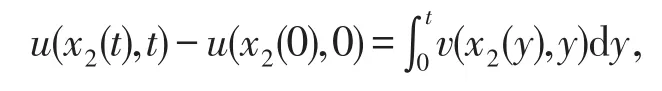
由初始条件知u(x2(0),0)=0,以及(2)可得

积分区域如图1所示,对于以上积分改变积分次序,可得
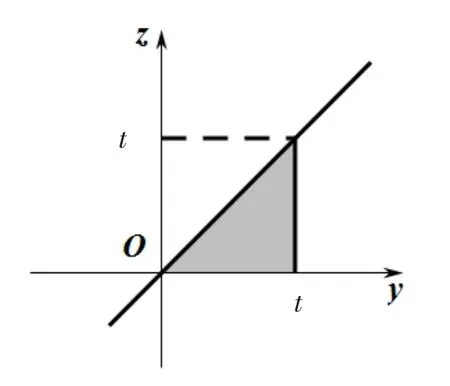
图1 积分区域
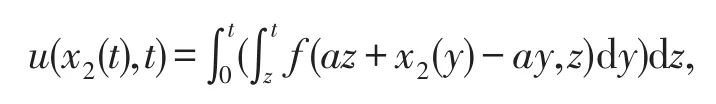
令η=az+x2(y)-y=az-2ay+C2,
即dη=-2ady,代入得
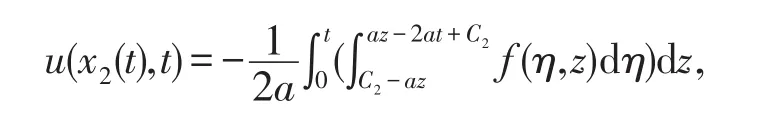
再由C2=x2(t)+at,带入上式得,

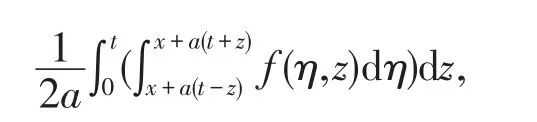
最终得到非齐次波动方程的解
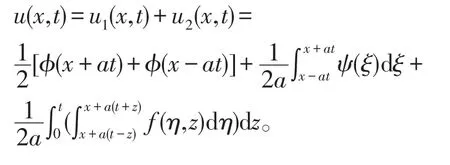
[1]樊龙.一维齐次波动方程Cauchy问题达朗贝尔公式的另一种推导[J].山西大同大学学报(自然科学版),2015(2):15-16.
[2]朱长江,邓引斌.偏微分方程[M].北京:科学出版社,2005:64-66.
[3]谷超豪,李大潜,陈恕行,等.数学物理方程[M].北京:高等教育出版社,2002:8-10.
The solution of One-dimensional Nonhomogeneous Wave Equation Which is Obtained by Using Characteristic Lines
FAN Long
(School of Coal Engineering,Shanxi Datong University,Datong Shanxi,037000)
For the problem of solving the nonhomogeneous wave equation,generally,we rely on the principle of Duhamel.In this paper,we change the form of the equation,the result of the equation can be obtained by using the method of characteristic lines.
nonhomogeneous wave equation;characteristic lines;general solution
O175.9
A
1674-0874(2016)01-0014-02
2015-03-07
樊龙(1989-),男,山西忻州人,硕士,助教,研究方向:双曲型偏微分方程。
〔责任编辑 高海〕
