一种基于属性变化的增量约简算法

程 妮

（运城学院公共计算机教学部，山西运城044000）

一种基于属性变化的增量约简算法

程 妮

（运城学院公共计算机教学部，山西运城044000）

随着处理数据工具的发展，许多数据库的属性都是动态增加的。当属性动态增加时，静态的约简方法消耗时间巨大，效率不高，针对这个缺陷，文中提出了属性变化的增量约简方法，通过增量技术计算增加属性后的知识粒度，然后在新的知识粒度和原有约简的基础上，能够在较短时间内找到新决策表的约简，仿真结果表明所提算法是有效的。

属性约简;增量学习;知识粒度;决策表;粗糙集

粗糙集是一种新的软计算工具用来分析和处理各种不确定性的、不精确的数据，已经引起国内外学者广泛重视，成功地应用到图像处理、特征选择、规则提取、知识发现等领域[1]。属性约简是粗糙集中的一个重要操作，它就是保持信息系统分类能力不变的情况，把不重要的和删除冗余的属性删掉。最近几年来很多研究者已经提出了大量约简方法。王磊[2]根据等价关系矩阵和知识粒度之间的关系，给出了属性增删时等价关系矩阵变化的规律，提出了基于知识粒度的矩阵属性约简方法；王国胤[3]从信息论观点出发对粗糙集理论的基本概念和主要运算进行分析讨论，提出了基于条件信息熵提出决策表的约简算法；梁吉业[4]提出了信息量的启发式属性约简算法，并通过实例说明该算法是有效的。上述的约简方法都为静态信息系统设计的，在实际中许多信息系统是随着时间变化而变化的，静态属性约简方法处理动态数据需要重新计算，造成时间和空间耗费巨大，故静态约简方法处理动态数据是无效的，为了克服这种缺陷，许多学者提出来增量约简方法。[5-7]

增量技术是处理动态变化的有效技术，许多研究者已经成功地把增量技术运用到的启发式属性约简中，并取得一定成果。我们发现大多增量约简知识粒度已经被广泛地应用到启发式约简中，由于很多数据库的属性随着时间的变化而增加，静态的约简算法需要消耗大量的时间和空间，为了克服缺陷，提高效率，本文在知识粒度概念的基础上，提出一种维度增量约简算法，当决策表的属性增加时，给出了增量计算知识粒度的相关定理和概念，并通过实验表明所提算法是有效性。

1 粗糙集的相关知识

定义1[1]：一个信息系统是四元组S=(U,A=C⋃D,V,f)，其中U是非空有限对象集合，也称为论域；其中C、D分别为条件属性集和决策属性集，其中Va是条件和决策属性a的值，f：U×C⋃D→V为信息函数，即a∈C⋃D，x∈U有f(x,a)∈Va。

定义2[6]：给出一个决策表S=(U,A=C⋃D,V,f)，论域为U，U∕C={X1,X2,…,Xm}，我们定义的知识粒度为

2 知识粒度约简算法

2.1 知识粒度基本知识

定义3[5]：给出一个决策表S=(U,A=C⋃D,V,f)，论域为U，C为条件属性集，D为决策属性集，则决策属性D关于条件属性C的相对知识粒度被定义为GD(D|C)=GD(C)-GD(C⋃D)。

定义4[5]：(属性重要度1)：给出一个决策表S=(U,A=C⋃D,V,f)，对于∀a∈C，属性a在条件属性C相对于决策属性集D的重要性被定义为：

定义5[5]：(属性重要度2)：给出一个决策表S=(U,A=C⋃D,V,f)，B⊆C，对于∀a∈C-B，属性集a在条件属性C相对于决策属性集D的重要性被定义为：

定义6[5]：给出一个决策表S=(U,A=C⋃D,V,f)，对 ∀a∈C，若GD(D|C)=GD(D|C-{a})，则称a是条件属性C相对于决策属性集D不必要的属性，否则称a是必要的属性。

性质1给出一个决策表S=(U,A=C⋃D,V,f)，对∀a∈C，属性a为决策表S的必要的属性，当且仅当Sig(a,C,D)＞0。

定义7[5]给出一个决策表S=(U,A=C⋃D,V,f)，决策表S的核为CoreC(D)={a∈C|Sig(a,C,D)＞0}。

定义8[1]给出一个决策表S=(U,A=C⋃D,V,f)，B⊆C，B为决策表S的属性约简当且仅当：（1）GD(D|B)=GD(D|C) ；（2）对于∀a∈B，使得GD(D|B-{a})≠GD(D|C)。

2.2 传统知识粒度约简算法

根据上面定义和概念，我们介绍一种传统的基于知识粒度的启发式约简如算法1所述[2]。

算法1：传统的基于知识粒度的启发式约简方法。

输入：给出一个决策表S=(U,A=C⋃D,V,f)；

输出：决策表S的属性约简REDC。

步骤1：计算决策表的核Core,令REDC←Core；

步骤2：如果GD(D|REDC)=GD(D|C)，然后转到步骤5，否则转到步骤3；

步骤3：P←REDC，当GD(D|P)≠GD(D|C)，根据定义5计算决策表属性子集C-P中每个属性a相对于P的重要性2，依次循环选取最大的属性重要性a0=max(Sigouteru(a,P,D),a∈P添加到P中，即P←P⋃{a0}，计算增加a0后的P的知识粒度直到与决策表的知识粒度相等为止；

步骤4：在决策表S中，从后向前依次遍历P中的每一个属性a，根据定义3计算P中删除属性a后的知识粒度GD(D|P-{a})，如果GD(D|P-a}){=GD(D|C)，则P←P-{a}；

步骤5：REDC←P，输出决策表的属性约简REDC。

3 知识粒度维度增量约简算法

当决策表的属性动态增加，用静态约简的方法计算增加后的属性约简耗费很多的空间和时间，为了克服这个缺陷，提高计算效率，能够在较短时间内找到增加属性后的约简，提出了属性变化的增量约简算法。

3.1 计算知识粒度增量机制

为了更好解释增量定理，下面通过实例来说明增加属性后等价类的增量变化，给出一个决策表S=(U,A=C⋃D,V,f)，U∕C={X1,X2,…,Xm}，P是新增加的属性集，等价类U C中的部分等价类由于增加属性P后其划分可能更细，而等价类U C中的另一部分等价类由于增加属性P后其划分可能不发生变化，所以我们可得表示增加属性P后发生细化的等价类，Xi(i=1,2,…,k)表示增加属性P后没有变化的等价类。

例1在表1中，论域为U={1,2,3,4,5,6,7,8,9}，U∕C={{1},{2,4},{3,5},{6,7},{8,9}}，增加属性集P={g,h}，且g={1,0,1,1,1,1,0,1,1}和h={0,1,0,1,1,0,1,0,0}，我们可得U∕C⋃P={{1},{2},{4},{3},{5},{6},{7},{8,9}}。

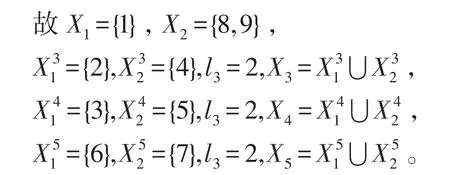
定理1给出一个信息系统S=(U,A=C⋃D,V,f)，U∕C={X1,X2,…,Xm}，P是新增加的属性集，可得则增加属性后的知识粒度为：

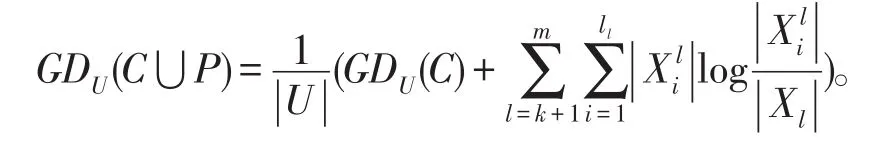
证明根据定义3我们可得：

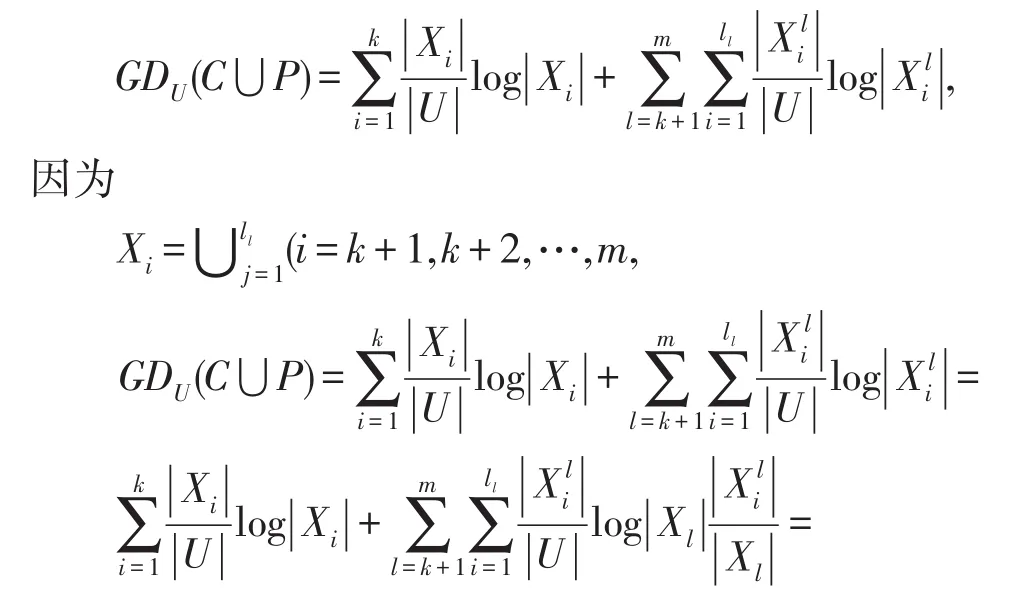
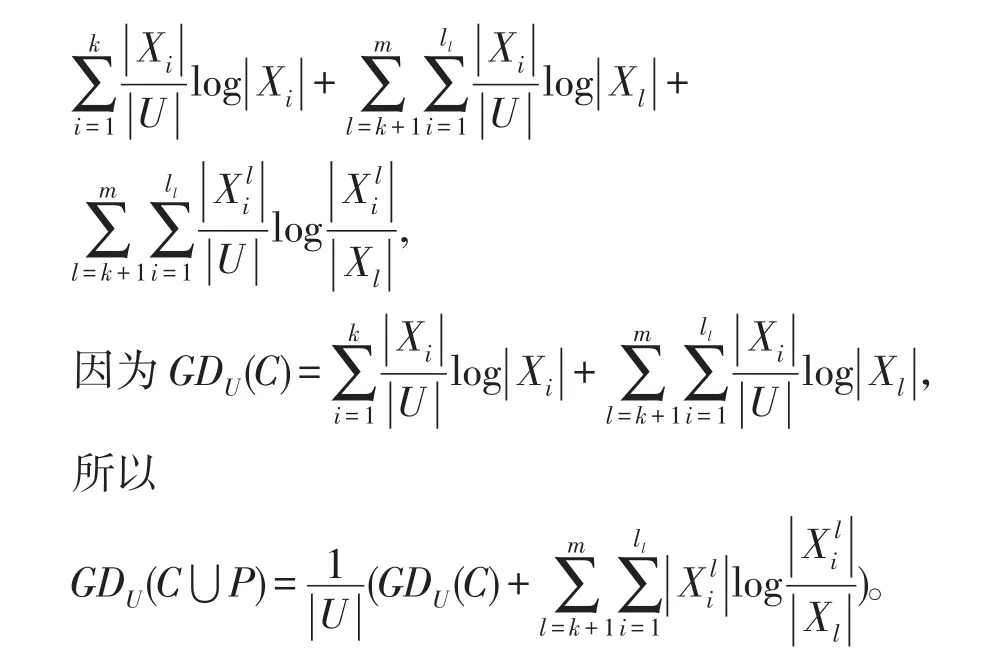
定理2给出一个信息系统S=(U,A=C⋃D,V,f)，U∕C⋃D={Y1,Y2,…,Ym}，P是新增加的属性集 ，可 得U∕C⋃P⋃D={Y1,Y2,…,Yk,则增加属性后的知识粒度为：

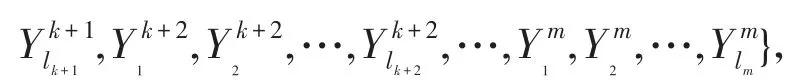
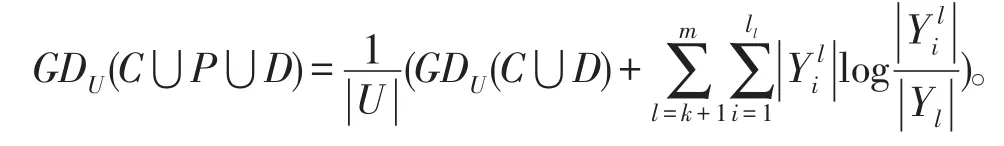
定理3给出一个信息系统S=(U,A=C⋃D,V,f)，U∕C={X1,X2,…,Xm}和U∕C⋃D={Y1,Y2,…,Ym}，P是新增加的属性集，可得U∕C⋃P={X1,X2,…,，则增加属性后的相对知识粒度为：

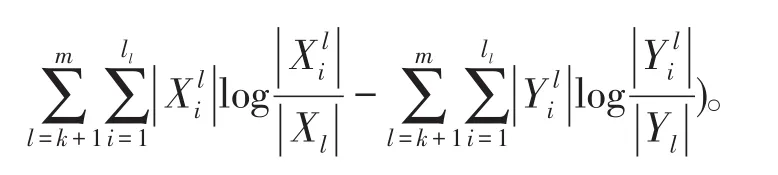
3.2 知识粒度维度增量约简算法

根据增量计算知识粒度的定理和概念，我们提出了一种基于知识粒度维度增量约简算法2描述如下：

算法2：一种属性变化的增量约简算法。

输入：给出一个决策表S=(U,A=C⋃D,V,f)，增加属性P前的属性约简RedC，新增属性P；

输出：决策表增加属性P后的属性约简RedC⋃P。

步骤1：B←REDC；计算新的等价类,

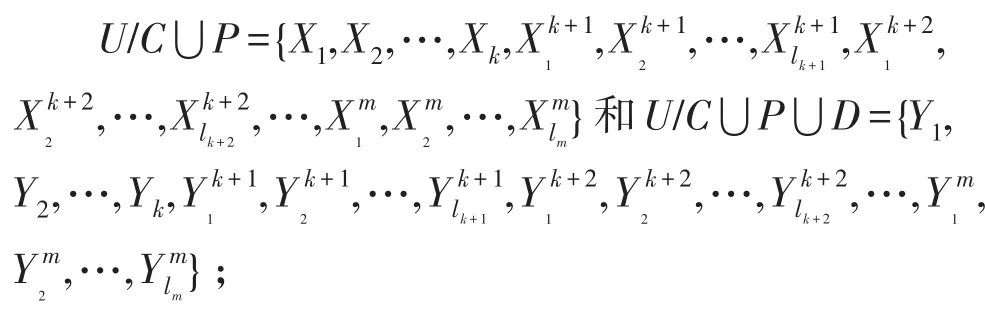
步骤2：根据定理3，计算增加属性后新的知识粒度GD(D|C⋃P)；

步骤3：如果GD(D|B)=GD(D|C⋃P)，然后转到步骤6，否则转到步骤4；

步骤4：当GD(D|B)≠GD(D|C⋃P)，根据定义5计算决策表属性子集C⋃P-B中每个属性a相对于P的重要性2，依次循环选取最大的属性重要性a0=max(Sigouter

u(a,B,D),a∈B添加到B中，即B←B⋃{a0}，计算增加a0后的B的知识粒度直到与增加属性后决策表的知识粒度相等为止；

步骤5：在决策表S中，从后向前依次遍历B中的每一个属性a，根据定义3计算B中删除属性a后的知识粒度GD(D|B-{a})，如果GD(D|B-{a})=GD(D|C⋃P)，则B←B-{a}；

步骤6：REDC⋃P←B，输出决策表增加属性后新的约简REDC⋃P。

非增量和增量约简算法的时间复杂度分析如下，当决策表增加了多个属性之后，徐章艳[7]在计算知识粒度的复杂度为为条件分类个数，非增量约简算法中步骤3到步骤4的时间复杂度为增量约简算法总的时间复杂度为维度增量约简算法中步骤3到步骤5的时间复杂度为为增加属性后可以细化的等价类的个数，增量约简算法总的时间复杂度为非增量和维度增量约简算法的时间复杂度比较如表1所示：

表1 非增量约简算法和增量约简算法时间复杂度比较

4 仿真分析

为了验证所提的增量方法比非增量方法的有效性，我们从UCI机器学习数据库中下载了Lung Cancer和ticdata2000两个数据集，数据描述如表2所示，分别用增量和非增量方法做实验，并对两种方法所花费的时间进行了比较，仿真所用的软件和硬件环境是：Windows 8操作系统，32-bits(JDK1.6.0_20)，CPU Pentium(R)Dual-Core E5800 3.20GHz，内存：Samsung DDR3 SDRAM 4.0GB。

表2 数据集描述

在仿真过程中，我们把每个数据集分成均匀两个部分，把第一部分作为基本数据集，把另一个数据集按20%、40%、60%、80%、100%依次添加到基本数据集中，比较增量和非增量所消耗的时间，实验结果如图1所示，其中纵轴表示所花费的时间，横轴表示增加的属性的百分数。

从图1可得，增量约简的方法所花费的时间远远小于非增量约简的方法所消耗的时间，验证了所提的增量方法是有效的。

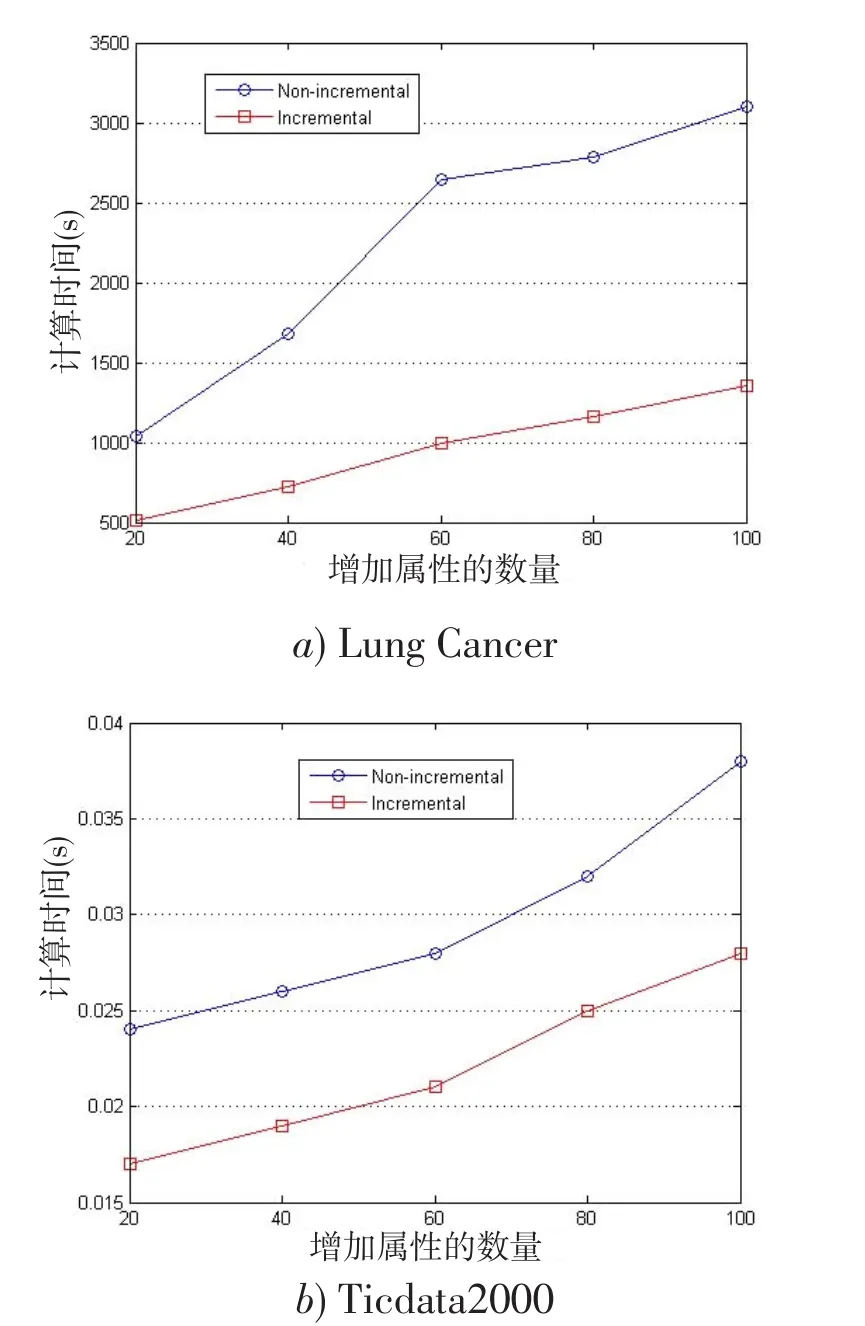
图1插入多个属性集增量和非增量约简算法消耗时间的比较

5 结语

在现实生活中，许多数据库的行和列都是动态增加的，由于静态方法计算属性约简需要耗费大量的时间和空间，为了克服缺陷，提高效率，本文在知识粒度概念的基础上，提出了一种属性变化的增量启发约简算法，当决策表属性动态增加时，通过增量机制计算增加后的知识粒度，然后在新的知识粒度和原来约简的基础上，能够在较短时间内找到增加属性后的约简，表明所提出的增量方法是有效性的，由于决策表属性值也是动态改变的，所以下一步研究工作是属性值动态改变的增量式约简算法。

[1]苖夺谦,范世栋.知识粒度的计算及其应用[J].系统工程理论与实践,2002,22(1)：48-56.

[2]王磊,叶军.知识粒度计算的矩阵方法及其在属性约简中的应用[J].计算机工程与科学,2013,35(3)：98-102.

[3]王国胤,于洪,杨大春.基于条件熵的决策表约简[J].软件学报,2002,25(7)：760-765.

[4]梁吉业,曲开社,徐宗本.信息系统的属性约简[J].系统工程理论与实践,2001,12：76-80.

[5]刘清.Rough set及Rough理 [M].北京：科学出版社,2001：7-16.

[6]YAO Y Y.Probabilistic approaches to rough sets[J].Expert Systems,2003,20(5)：287-297.

[7]徐章艳，刘作鹏，杨炳鲁，等.一个复杂度max(O(|C||U|,O(|C|2|U∕C|))的快速约简算法[J].计算机学报,2006,29(3)：391-398.

An Incremental Reduction Approach with Variation of Attribute Set

CHENG Ni
(Department of Public Computer Teaching,Yuncheng University,Yuncheng Shanxi，044000)

With the rapid development of data processing tools,many data sets in databases increase quickly in attributes.In this paper,we propose incremental reduction approach based on knowledge granularity when multiple attribute are added to decision table.Incremental mechanisms to calculate the new knowledge granularity are first introduced,Then,the proposed incremental method can find the new reduct in a much shorter time based on knowledge granularity and reduct of the original decision table.Finally,the experiments show that the developed algorithm is effective and efficient.

attribute reduction;incremental learning;knowledge granularity;decision table;rough set

TP311

A

1674-0874(2016)01-0003-05

2015-10-24

山西省高等学校教学改革项目[J2014106]；运城学院教学改革项目[JG201429]

程妮（1986-），女，山西运城人，硕士，助教，研究方向：计算机应用技术。

〔责任编辑 高海〕