基于管土耦合作用的海底管道稳定性分析研究

刘晓峰， 杨树耕， 王　晗， 徐　蒙

(天津大学 水利工程仿真与安全国家重点实验室， 天津 300072)



基于管土耦合作用的海底管道稳定性分析研究

刘晓峰， 杨树耕， 王晗， 徐蒙

(天津大学 水利工程仿真与安全国家重点实验室， 天津 300072)

海底管道作为水下油气运输系统中重要的组成部分，其稳定性研究尤为重要。通过有限元软件ABAQUS，模拟铺设后未运行以及输送石油过程中的海床-管道耦合作用系统。通过对土体进行初始的应力平衡、管道自重载荷分析、管道-土体相互接触作用分析、内压载荷分析、水平屈曲分析，分别计算管道在铺设完成后及实际运行过程中的位移及应力。计算结果表明，管道运行中的温度差和压力差引起的大变形是导致管道失效的最主要原因。同时通过对比研究可知，海床土体的相关参数对管线发生屈曲变形都有不同程度的影响，影响的强弱程度取决于土体的刚度以及土体对管道水平向的抗力作用。

海底管道；海床土体；水平屈曲；稳定性；管土耦合

0　引言

随着海洋资源的不断开发，海洋工程逐步向深海领域发展。作为海洋油气集输与储运的重要组成部分，海底管道已成为深海海底油气田开发工程中的重要环节。由于深海海底环境复杂多变，土体特性及物理指标很大程度上不同于浅海土体，因此，研究深海海底管道在位稳定性显得尤为重要。

吴鑫[1]研究了管道在自重和静水压力作用下的沉降过程，但其研究是在静态载荷作用下的，并未考虑管道与土体之间接触面的相互作用。任艳荣[2]运用有限元法研究海底管线在砂质海床条件下的稳定性问题，但在计算中仍未考虑管线与海床接触问题，对管道的运动情况没有进行讨论。白云川[3]研究了管线和砂质海床间的相互作用，但并未综合考虑环境载荷。唐丕鑫[4]运用ABAQUS软件研究了管线在海底的自沉过程，但仅考虑了铺设后尚未运行的阶段。刘润[5]对高温高压作用下海底管道的竖向屈曲、水平屈曲进行了分析。在以上研究的基础上，以南海深海区为研究背景，对管道铺设后状态以及运行中状态进行数值模拟，并进行相应的数据分析，从而为实际应用提供参考借鉴。

1　有限元模型

1.1管道模型

为了使模型更加接近实际情况，管线采用三维实体模型，管道钢材的材料应力-应变关系采用Ramberg-Osgood本构模型。根据《海底管道系统规范》以及《输油管道设计规范》中关于海底管道的相关要求，海床土体的各项物理指标参数以及海底管道的规格参数见表1。

表1　管线模型参数

1.2海床土体模型

由于管土之间的相互作用较为复杂，选择恰当的土体本构模型非常重要，采用Mohr-Coulomb模型作为研究的本构模型，按照Mohr-Coulomb破坏和强度准则进行研究，海床土体模型参数见表2。

土体模型的几何尺寸选取也十分关键，既要排除边界效应对计算结果的影响，又要使模型尽可能的简化以减小计算成本。参考已有结果，选取土体的宽度为15 m，高度为1.5 m。

表2　海床土体模型参数

1.3计算载荷

由于模拟的是南海深海区域海底环境，其所受环境载荷与浅海区域大不相同。参考已有的现场数据和研究成果发现：在水深较深的海底，风载荷作用消失；波浪在深海海底无法形成和传播，故波浪载荷可以忽略不计；海流在深海海底的速度很小，所形成的海流载荷也可忽略不计。因此该文在计算过程中，忽略相应的风载荷、波浪载荷以及海流载荷。

同时，研究需要综合考虑管道在铺设后尚未运行以及输送石油过程中的状态。因此，在尚未运行状态，管道所受载荷主要包括管线及配载重量所受到的浮力。

而在管道使用过程中，除了上述载荷外，由于管道内部输送石油的温度及压强较大，管道的体积将会发生膨胀，在管土的耦合作用以及管道边界约束作用下会产生较大的轴向力，所以管道内外的温差和压差所产生的轴向力是主要载荷。

采用《输送管道设计规范》中的管道极限内压公式[6]：

(1)

式中：P为设计内压力； [σ]为海底管道的许用应力；D为海底管道的外径； δ为海底管道壁厚。

根据公式求出极限输送压力Ppcr为 65.96 MPa,设计压力为20 MPa，该文模拟的水域深度为1 550 m，计算出海底管道外部所受压力为15.57 MPa，则管道在运行状态下，内外部所受压力差为 4.43 MPa。

海底管道在温度作用下产生的最大轴向力FT为[7]：

(2)

式中： α为海底管道的热膨胀系数,取0.000 011 5；E为海底管道材料的杨氏模量；ΔT为海底管道运行状态的内外温度差，设计温差为68°；A为海底管道的横截面面积。

1.4管土接触作用

海底管道的稳定性问题要考虑管土耦合作用,在ABAQUS软件计算中，需要设置模拟接触过程。该文采用单纯的主-从接触算法，即在一个表面(从属面)上的节点不能侵入另一个表面(主控面)的任何部分。该算法并没有对主面做任何限制，它可以在从面的节点之间侵入主面。主从面的选取需遵循以下原则：(1)从面应该是网格划分更精细的表面；(2)如果网格密度相近，从面应该选取采用较软材料的表面。因此，在该模型中，选取管道下半部分作为主面，海床土体上表面作为从面。

1.5网格划分

在网格划分时，管道与土体均采用八节点六面体线性减缩积分(C3D8RP)单元，并对管道与土体接触的局部区域进行细化，海底管道管土耦合作用有限元模型如图1所示。

图1　管土耦合作用模型

2　计算结果与分析

2.1地应力平衡

进行海床土体与管道接触作用之前，要进行初始地应力平衡，初始地应力平衡的目的是使数值模拟获得一个存在的初始应力，而且不存在初始应变的状态。输入关键词语句，经过ABAQUS软件的计算，得到了同时满足平衡条件和屈服条件的初始地应力场。海床土体经过初始地应力平衡后的位移分布如图2所示，Mises应力分布如图3所示。

图2　地应力平衡后的土体位移分布

图3　地应力平衡后的土体Mises应力分布

由图2可知，经过初始地应力平衡后，海床土体在竖直方向存在微小位移，土体上表面的位移为3.06×10-10m，土体底面的竖直位移接近于0。位移沿竖直方向自上而下呈递减趋势，并且稳定于2×10-10m。进行平衡之后土体的初始位移数量级较小，与实际工程相比，此位移可忽略不计，对后续的工作基本无影响。

由图3可知，经过初始地应力平衡后，海床土体上表面的Mises应力为1.296×104Pa，土体底面的Mises应力为6.17×104Pa。由此可知，Mises应力沿竖直方向自上而下呈递增趋势，数量级由104Pa逐渐增大到105Pa 。经过对地应力的初始平衡后，土体的变形及位移都可以接受，结果较为理想，且形成了一个同时满足平衡条件和屈服条件的地应力场，满足实际工程的要求。

2.2自重载荷分析

完成初始地应力平衡之后，引入管道-土体相互接触作用，并施加管道配重载荷以及浮力，进行相应计算，得到管道在安装之后未运营状态的位移分布，如图4所示。海床土体的竖直方向的位移分布，如图5所示。

图4　自重载荷下管道的位移分布

图5　自重载荷下海床土体的位移分布

在施加管道自重载荷以及浮力载荷后，海底管道竖直方向出现一定位移，形成沉降效应。由图4可知，管道在竖直方向的位移为 7.69×10-3m，约占管道壁厚的15%，对管道竖直方向的稳定性产生较大的影响。同时，受到管线自重载荷的影响，与管道相接触的海床土体也会发生相应变形。海床土体的变形情况要比管道的变形复杂，不仅在以管道和土体接触为中心的区域产生变形，管道两侧的土体也会因管道的沉降产生一定的变形。在海床土体与管道接触的区域，土体呈现了水滴状的变形，最大的沉降量出现在土体的上表面，为3.71×10-4m ，此变形小于管道的沉降量，说明管道从铺置到完全稳定的过程中，自身一部分已埋入土体内。随着管道的埋入，下方土体受到管道自重载荷作用产生沉降，使得管道两侧的土体受到挤压，从而产生了抬升，抬升的土体又会继续影响周围土体而产生微小位移，从而形成波浪状的位移分布。管道两侧的土体发生隆起后，会形成小土坡，土坡的存在会对管道水平方向起到一定约束作用。

2.3内压载荷分析

完成管道未运行状态的计算后，对工作状态下的管线进行模拟分析。施加石油介质的自重，并施加管线在运行过程中的内压载荷，管道在内压状态下的应力云图如图6所示。

图6　内压载荷下管道的Mises应力分布

内压载荷作用在海底管道的内表面上，此时管道内表面压力最大值为31.92 MPa，外表面的压力为26.31 MPa。

2.4管道水平屈曲分析

施加温度作用下产生的轴向力，并将管道两端设置为固定约束，对管道在内压和温度作用下进行应力-应变分析，经过计算得到管道在水平方向的位移，部分管道的水平位移及Mises应力如图7、图8所示。

图8　海底管道后屈曲Mises应力分布

图8　海底管道后屈曲Mises应力分布

由图7可以看出，在内压和温度应力的联合作用下，海底管道在水平方向上发生了屈曲变形，沿管道轴线方向一条直线上每隔0.5 m取一节点，得到管道在轴向方向的不同位置的位移，如图9所示。

从图9可以看出，海底管道在温度和压差的作用下，发生了局部屈曲变形，变形挠曲线关于管道中点对称，管道端部位移为0，最小水平位移为-0.146 768 m，出现在距离管道两端15.5m处，最大水平位移为0.139 348 m，出现在距离管道两端45.5 m处。发生水平屈曲的管道长度为30 m，相对位移为0.286 116 m。

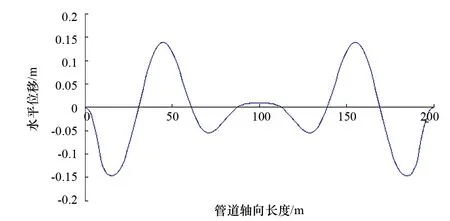
图9　管道沿轴向长度的水平位移曲线

3　参数变化的影响与分析

3.1土体杨氏模量的变化

改变计算模型中海床土体的杨氏模量大小，其余参数的设置均无变化，分别对管道进行水平屈曲计算分析。通过多次计算，最终得到管道随着土体杨氏模量的水平位移变化。图10为管道水平相对位移随土体杨氏模量的变化图。

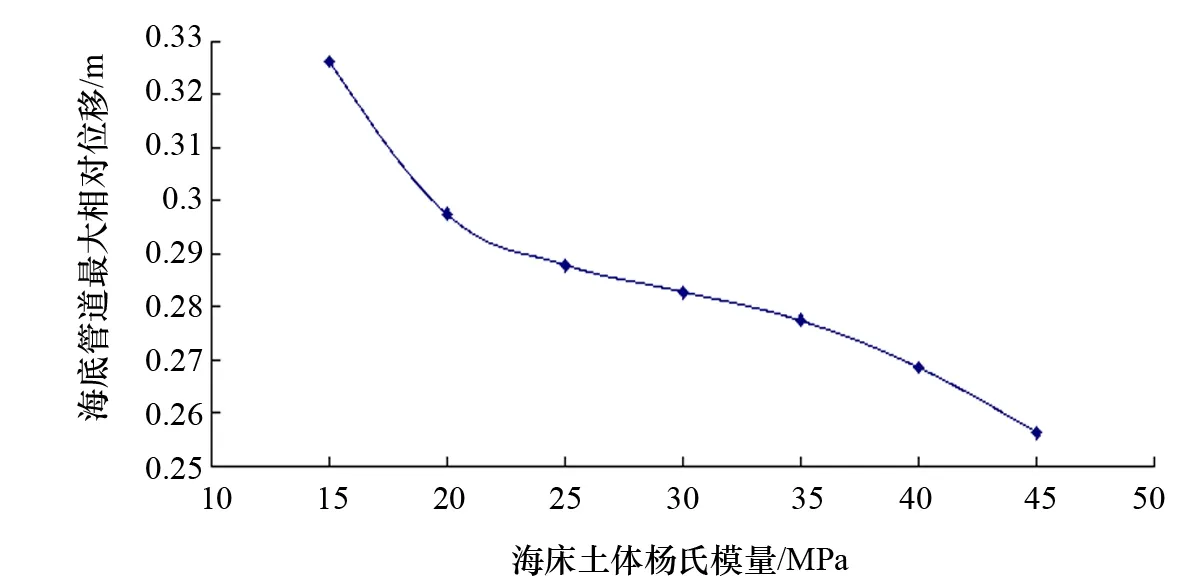
图10　管道水平相对位移随土体杨氏模量的变化图

由图10可以看出，针对不同海床土体杨氏模量进行计算后，管道均发生不同程度的水平屈曲，水平方向的相对位移量均保持在0.1 m的数量级，而且随着土体杨氏模量的增大而减小。当土体的杨氏模量较小时，相对位移变化幅度较大；当杨氏模量慢慢增大时，相对位移随杨氏模量变化的幅度趋于平缓。通过分析可知：海床土体的杨氏模量较小时，土体的刚度较小，容易发生变形，其对管道的横向抗力较小；当土体的弹性模量逐渐增大时，其刚度也随之增大，对管道的横向约束作用增大，从而可减小管道屈曲变形的幅度，一定程度上增强了海底管道运行状态的稳定性，但并不能使其水平向的相对位移明显减小，故对其整体稳定性的影响不大。

3.2土体密度的变化

改变计算模型中海床土体的密度大小，其余参数的设置均无变化，分别对管道进行水平屈曲计算分析。通过多次计算，最终得到管道随土体密度的水平位移变化，如表3所示。

表3　不同土体密度下海底管道的水平相对位移

由表3可以看出，针对不同海床土体密度进行计算后，管道均发生水平屈曲，水平方向的相对位移量均保持在0.282 5 m左右，而且管道的水平相对位移不会随着土体密度的变化而变化。海床土体的密度并不能决定土体的刚度以及其他力学性质，因而不会改变土体对管道的横向约束作用。所以，海床土体密度的变化不会对海底管道水平屈曲的形态造成影响。

3.3土体管道摩擦系数的变化

改变计算模型中海床土体的摩擦系数大小，其余参数的设置均无变化，分别对管道进行水平屈曲计算分析，通过多次计算，最终得到管道随着土体摩擦系数的水平位移的变化。图11为管道水平相对位移随土体摩擦系数的变化图。

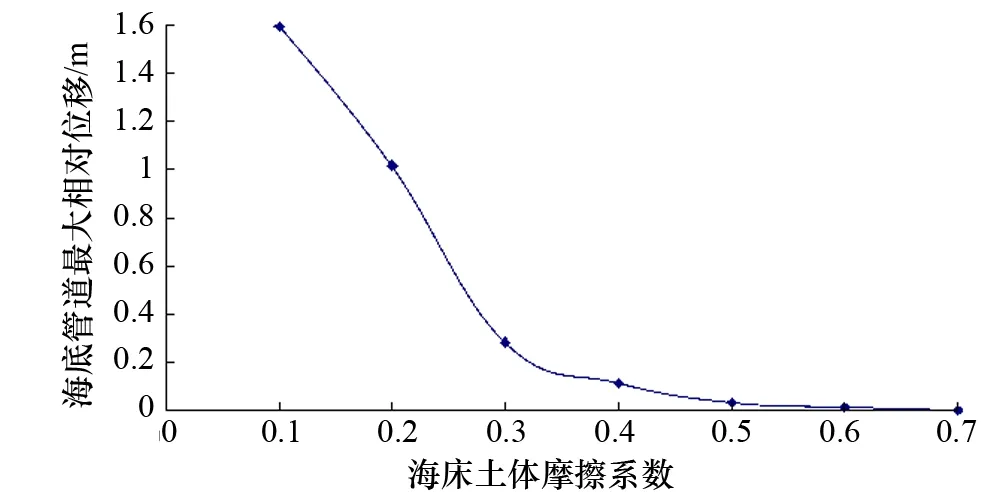
图11　管道水平相对位移随土体摩擦系数的变化图

由图11可以看出，针对不同海床土体摩擦系数进行计算后，管道均发生不同程度的水平屈曲，管道的水平相对位移随着土体摩擦系数变化幅度较大。当土体摩擦系数为0.1时，管道的相对水平位移可达到1.6 m，变形较大，对管道稳定性和安全性产生较大影响。随着摩擦系数增大，管道水平方向的相对位移减小，而且变化的幅度较为明显。

3.4土体泊松比的变化

改变计算模型中海床土体的泊松比大小，其余参数的设置均无变化，分别对管道进行水平屈曲计算分析，通过多次计算，最终得到管道随着土体泊松比的水平位移的变化，如图12所示。

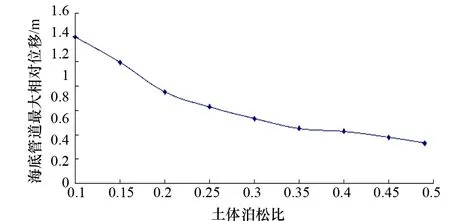
图12　管道水平相对位移随土体泊松比的变化图

由图12可以看出，针对不同海床土体泊松比进行计算后，管道均发生不同程度的水平屈曲，水平方向的相对位移量均保持在0.2 m～0.5 m之间，而且随着土体泊松比的增大而减小。当土体的泊松比较小时，海底管道的水平相对位移较大，屈曲变形较明显，当土体的泊松比较大时，海底管道的水平相对位移较小。进一步分析可知，土体泊松比的大小决定了土体横向应变与纵向应变的比值，即土体横向变形分担纵向变形的影响值。泊松比变大，则横向变形分担纵向变形的能力较强，管道在挤压两侧土体时，土体在水平方向发生的弹性变形较小，因此对管道的横向约束作用较强。

4　结论

(1) 通过ABAQUS软件对管土耦合作用下的海底管道未运行状态及工作状态进行建模，通过地应力平衡、自重载荷分析、管土相互作用设置、内压载荷分析、水平屈曲分析，计算得到了海底管道运行中高温高压作用下的水平屈曲位移，研究结果与实际差别不大，具备一定实际应用价值。

(2) 管道在运行状态中，水平方向的大变形主要由管道内外温度差和压力差产生的轴向膨胀力引起，而最终的位移大小除受轴向力的影响外，还受到管道两侧土体对管道的水平约束作用。

(3) 通过对比研究发现：海床土体的杨氏模量、泊松比以及土体与管道的摩擦系数对管道最终的变形均会产生不同程度的影响，影响的大小程度取决于土体对管道横向抗力的大小，参数的改变使得土体自身刚度变大，不容易进入塑性状态，则对管道的水平约束作用较大，从而能够在一定程度上减小管道屈曲的位移幅值。在这些参数中，土体和管道的摩擦系数对管道屈曲的变化影响最大，在管道实际设置过程中，要特别注意土体的物理指标，选取海床土体刚度较大的区域，能够有效保证管道运营的稳定和安全。

[1]吴鑫.砂质海底管土相互作用有限元分析[D].北京：中国科学院力学研究所，1999 .

[2]任艳荣，刘玉标，顾小芸. 利用ABAQUS软件分析砂质海底管线稳定性[J]. 中国海洋平台，2001,16(5)：68-72.

[3]白玉川，杨细根，冀自青. 波浪条件下海底管线与沙质海床间的相互作用[J]. 天津大学学报，2011,57(1)：64-68.

[4]唐丕鑫，杨树耕. 海底裸置与埋置管线自沉过程对比研究[J]. 海洋工程，2015，33(2)：89-96.

[5]刘润.郭林坪.温度应力下海底管道水平屈曲分析[J].中国科技论文在线，2011，6(5):368-372.

[6]Tom R G, Per M A. Buckling of buried pipelines under transportation of heated oil and gas [C]. The International Society of Offshore and Polar Engineers, 1990.

[7]Gary C, Andrew R. Euler buckling of idealized horizontal pipeline imperfections [C]. Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering, 2010.

The Study of Stability of Pipeline Based on Coupling Effect of Soil and Pipeline

LIU Xiao-feng， YANG Shu-geng， WANG Han, XU Meng

(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University, Tianjin 300072, China)

As an important component of the offshore oil and gas transportation system, submarine pipeline's stability plays a critical role in production system. Through finite element software ABAQUS, a seabed soil-pipe coupling system model was established in operation condition and out of service .Through balancing the seabed soil in-situ stress, analyzing self-loading of pipeline, setting seabed soil-pipe contact, studying internal pressure of pipeline, researching Pipeline buckling, displacement distribution and stress distribution can be calculated in operation condition and out of service. The analysis results show, large deformation caused by temperature difference and pressure difference is the most important reason of failure situations of pipeline. At the same time, by comparing the simulation research, we can conclude that The parameters of the seabed soil, makes a difference on the Buckling of pipe differing in degree.The size of the effect depends on stiffness of the seabed soil and lateral soil resistance acting on the pipeline.

submarine pipeline; seabed soil; lateral buckling; stability; coupling of soil and pipeline

2015-09-24

国家重点基础研究发展计划(973)资助项目(2014CB046802)。

刘晓峰(1990-)，男，硕士研究生。

1001-4500(2016)04-0052-07

P75

A